7.4一元一次方程的应用——等积变形问题(22张PPT)
文档属性
| 名称 | 7.4一元一次方程的应用——等积变形问题(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-19 00:00:00 | ||
图片预览







文档简介
课件22张PPT。一元一次方程的应用 商店对某种商品进行调价,决定按原价的九折出售,此时该商品的利润率是15℅,已知这种商品每件的进货价为1800元,求每件商品的原价。解 设商品的原价为x元,根据题意,得
90℅x=1800(1+15℅)解这个方程,得x=2300所以,每件商品的原件为2300元。售价=成本×(1+利润率) 在有关营销问题中,一般要涉及到成本、售价、利润。它们的关系是:利润=售价-成本,利润率=利润/成本×100℅,售价=成本×(1+利润率)。
有时可以用“进货价”代替“成本”。但是,成本除包括进货价外,还应包括诸如运输费、仓储费、损耗、职工工资等。加油站复习:常用几何图形的计算公式长方形的周长 =
长方形的面积 =
三角形的面积 =
圆的周长=
圆的面积=
长方体的体积 =
圆柱体的体积 =
(长+宽) ×2
长 ×宽
×底×高
2πr(其中r是圆的半径)πr2长×宽×高 底面积×高=π r2h
(这里r为底面圆的半径,h为圆柱体的高)想一想: 请指出下列过程中,哪些量发生了变化,哪些量保持不变?
1、把一小杯水倒入另一只大杯中;
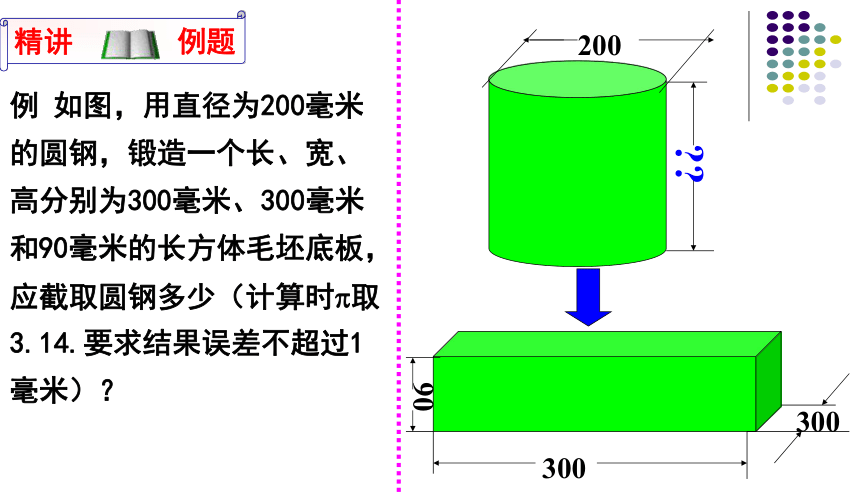
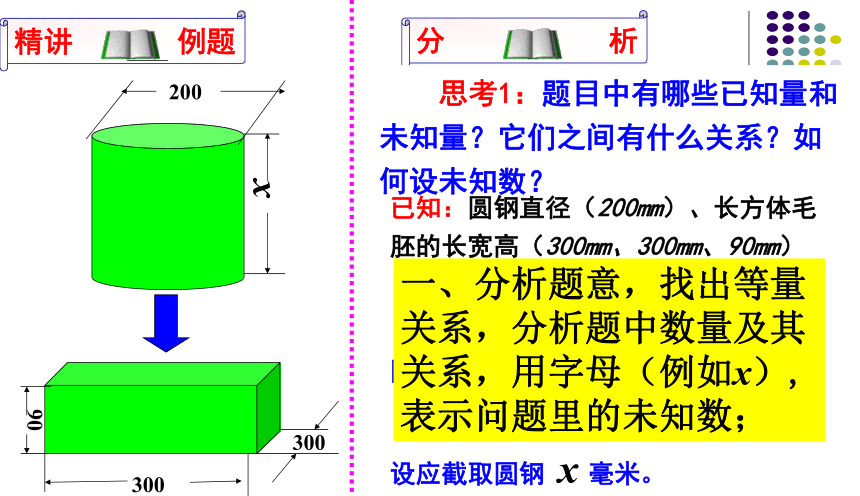
2、用一块橡皮泥先做成一个立方体,再把它改变成球。解:水的底面积、高度发生变化,水的体积和质量都保持不变 解:形状改变,体积不变例 如图,用直径为200毫米的圆钢,锻造一个长、宽、高分别为300毫米、300毫米和90毫米的长方体毛坯底板,应截取圆钢多少(计算时?取3.14.要求结果误差不超过1毫米)? 思考1:题目中有哪些已知量和未知量?它们之间有什么关系?如何设未知数?已知:圆钢直径(200mm)、长方体毛胚的长宽高(300mm、300mm、90mm)
未知:圆钢的高
相等关系:
圆钢体积=长方体毛胚的体积
设未知数:
设应截取圆钢 x 毫米。一、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如x),表示问题里的未知数; 思考2:如何用字母(未知数x)表示圆钢的体积?二、用含未知数x的一次式表示有关的量;圆钢的体积=? x 立方毫米思考3:如何根据等量关系“圆钢体积=长方体毛胚的体积”列出方程?三、根据等量关系列出方程; 根据等量关系列出方程,得:
?? ? x =300×300×80 思考4:如何解这个方程?四、解方程,求出未知数的值;
五、检验求得的值是否正确和符合实际情形,并写出答案. ? × x =300×300×90
方程化简为?x =810 解得 x≈258例 如图,用直径为200毫米的圆钢,锻造一个长、宽、高分别为300毫米、300毫米和80毫米的长方体毛坯底板,应截取圆钢多少(计算时?取3.14.要求结果误差不超过1毫米)?一、分析题意,找出等量关系 :
圆钢体积 = 长方体毛坯体积,
设应截取圆钢长为x毫米
二、用含未知数的式子表示有关的量:是指圆钢的体积是 ?(200/2)2 x立方毫米 .
三、根据等量关系列出方程,得:
? ×(200/2)2 ? x = 300×300×90
四、解方程求出未知数的值即解这个方程得:
x ? 258
五、检验求得的值是否正确和符合实际情形,并写出答案:应截取圆钢的长为258毫米.解:设应截取的圆钢长为x 毫米,根据题意得:
? ?(200/2)2 ? x = 300 × 300 × 80
3.14 x=720
x ? 230
答:应截取圆钢的长为230毫米 .变形前的体积(周长)=变形后的体积(周长)等积变形问题的等量关系列一元一次方程解应用题的一般步骤:
1、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如 x),表示问题里的未知数.
2、用代数式表示有关的量.
3、根据等量关系列出方程.
4、解方程,求出未知数的值.
5、检验求得的值是否正确和符合实际情形,并写出答案.归 纳1.将一个底面直径为10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径是20厘米的“矮胖”形圆柱,高变成了多少?锻压等量关系:变形前的体积=变形后的体积 解:设锻压后圆柱的高为x厘米,填写下表: 5厘米10厘米 36厘米 x厘米 等量关系:锻压前的体积=锻压后的体积× 52×36× 102 ? x根据等量关系,列出方程:解得: x =99因此,高变成了 厘米 列方程时,关键是找出问题中的等量关系。2.已知一圆柱形容器底面半径为0.5m,高为1.5m,里面盛有1m深的水,将底面半径为0.3m,高为0.5m的圆柱形铁块沉入水中,问容器内水面将升高多少? 1.5m0.5m0.5m0.3m1m分析: 根据以上演示我们知道了它们的等量关系:
水位上升部分的体积=小圆柱形铁块的体积
圆柱形体积公式是_______,
水升高后的体积 小铁块的体积
(__________) (________________)
解:设水面将升高x米, 根据题意得
方程为:___________________
解这个方程:__________
答:______________________?r2h0.52 ?X0.32 ×0.5 ?0.52 ?X = 0.32 ×0.5 ?X =0.18容器内水面将升高0.18m。一圆柱形容器的内半径为3厘米,内壁高30厘米,容器内盛有15厘米高的水。现将一个底面半径为2厘米、高18厘米的金属圆柱竖直放入容器内,问容器的水将升高多少米?分析:本题涉及圆柱的体积v= π r2h,这里r是圆柱底面半径,h为圆柱的高。一个金属圆柱竖直放入容器内,会出现两种可能:
(1)容器内的水升高后不淹没放入的金属圆柱;(2) 容器内的水升高后 淹没放入的金属圆柱 。
因此列方程求解时要分两种情况。解 设容器内放入金属圆柱后水的高度为x厘米。
(1)如果容器内的水升高后不淹没放入的金属圆柱,
根据题意,得 π·(32-22)·x= π 32×15
解这个方程,得x=27因为27>28,这表明此时容器内的水已淹没了金属圆柱,不符合题意,应舍去。(2)如果容器内的水升高后淹没放入的金属圆柱,
根据题意,得
π · 32 · x= π · 32×15+ π ·22×18解这个方程,得
x=23
23-15=8所以,容器内的水升高8厘米。小结:说说列方程解应用题的一半步骤:列一元一次方程解应用题的一般步骤:
1、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如x),表示问题里的未知数.
2、用代数式表示有关的量.
3、根据等量关系列出方程.
4、解方程,求出未知数的值.
5、检验求得的值是否正确和符合实际情形,并写出答案.
90℅x=1800(1+15℅)解这个方程,得x=2300所以,每件商品的原件为2300元。售价=成本×(1+利润率) 在有关营销问题中,一般要涉及到成本、售价、利润。它们的关系是:利润=售价-成本,利润率=利润/成本×100℅,售价=成本×(1+利润率)。
有时可以用“进货价”代替“成本”。但是,成本除包括进货价外,还应包括诸如运输费、仓储费、损耗、职工工资等。加油站复习:常用几何图形的计算公式长方形的周长 =
长方形的面积 =
三角形的面积 =
圆的周长=
圆的面积=
长方体的体积 =
圆柱体的体积 =
(长+宽) ×2
长 ×宽
×底×高
2πr(其中r是圆的半径)πr2长×宽×高 底面积×高=π r2h
(这里r为底面圆的半径,h为圆柱体的高)想一想: 请指出下列过程中,哪些量发生了变化,哪些量保持不变?
1、把一小杯水倒入另一只大杯中;
2、用一块橡皮泥先做成一个立方体,再把它改变成球。解:水的底面积、高度发生变化,水的体积和质量都保持不变 解:形状改变,体积不变例 如图,用直径为200毫米的圆钢,锻造一个长、宽、高分别为300毫米、300毫米和90毫米的长方体毛坯底板,应截取圆钢多少(计算时?取3.14.要求结果误差不超过1毫米)? 思考1:题目中有哪些已知量和未知量?它们之间有什么关系?如何设未知数?已知:圆钢直径(200mm)、长方体毛胚的长宽高(300mm、300mm、90mm)
未知:圆钢的高
相等关系:
圆钢体积=长方体毛胚的体积
设未知数:
设应截取圆钢 x 毫米。一、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如x),表示问题里的未知数; 思考2:如何用字母(未知数x)表示圆钢的体积?二、用含未知数x的一次式表示有关的量;圆钢的体积=? x 立方毫米思考3:如何根据等量关系“圆钢体积=长方体毛胚的体积”列出方程?三、根据等量关系列出方程; 根据等量关系列出方程,得:
?? ? x =300×300×80 思考4:如何解这个方程?四、解方程,求出未知数的值;
五、检验求得的值是否正确和符合实际情形,并写出答案. ? × x =300×300×90
方程化简为?x =810 解得 x≈258例 如图,用直径为200毫米的圆钢,锻造一个长、宽、高分别为300毫米、300毫米和80毫米的长方体毛坯底板,应截取圆钢多少(计算时?取3.14.要求结果误差不超过1毫米)?一、分析题意,找出等量关系 :
圆钢体积 = 长方体毛坯体积,
设应截取圆钢长为x毫米
二、用含未知数的式子表示有关的量:是指圆钢的体积是 ?(200/2)2 x立方毫米 .
三、根据等量关系列出方程,得:
? ×(200/2)2 ? x = 300×300×90
四、解方程求出未知数的值即解这个方程得:
x ? 258
五、检验求得的值是否正确和符合实际情形,并写出答案:应截取圆钢的长为258毫米.解:设应截取的圆钢长为x 毫米,根据题意得:
? ?(200/2)2 ? x = 300 × 300 × 80
3.14 x=720
x ? 230
答:应截取圆钢的长为230毫米 .变形前的体积(周长)=变形后的体积(周长)等积变形问题的等量关系列一元一次方程解应用题的一般步骤:
1、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如 x),表示问题里的未知数.
2、用代数式表示有关的量.
3、根据等量关系列出方程.
4、解方程,求出未知数的值.
5、检验求得的值是否正确和符合实际情形,并写出答案.归 纳1.将一个底面直径为10厘米,高为36厘米的“瘦长”形圆柱锻压成底面直径是20厘米的“矮胖”形圆柱,高变成了多少?锻压等量关系:变形前的体积=变形后的体积 解:设锻压后圆柱的高为x厘米,填写下表: 5厘米10厘米 36厘米 x厘米 等量关系:锻压前的体积=锻压后的体积× 52×36× 102 ? x根据等量关系,列出方程:解得: x =99因此,高变成了 厘米 列方程时,关键是找出问题中的等量关系。2.已知一圆柱形容器底面半径为0.5m,高为1.5m,里面盛有1m深的水,将底面半径为0.3m,高为0.5m的圆柱形铁块沉入水中,问容器内水面将升高多少? 1.5m0.5m0.5m0.3m1m分析: 根据以上演示我们知道了它们的等量关系:
水位上升部分的体积=小圆柱形铁块的体积
圆柱形体积公式是_______,
水升高后的体积 小铁块的体积
(__________) (________________)
解:设水面将升高x米, 根据题意得
方程为:___________________
解这个方程:__________
答:______________________?r2h0.52 ?X0.32 ×0.5 ?0.52 ?X = 0.32 ×0.5 ?X =0.18容器内水面将升高0.18m。一圆柱形容器的内半径为3厘米,内壁高30厘米,容器内盛有15厘米高的水。现将一个底面半径为2厘米、高18厘米的金属圆柱竖直放入容器内,问容器的水将升高多少米?分析:本题涉及圆柱的体积v= π r2h,这里r是圆柱底面半径,h为圆柱的高。一个金属圆柱竖直放入容器内,会出现两种可能:
(1)容器内的水升高后不淹没放入的金属圆柱;(2) 容器内的水升高后 淹没放入的金属圆柱 。
因此列方程求解时要分两种情况。解 设容器内放入金属圆柱后水的高度为x厘米。
(1)如果容器内的水升高后不淹没放入的金属圆柱,
根据题意,得 π·(32-22)·x= π 32×15
解这个方程,得x=27因为27>28,这表明此时容器内的水已淹没了金属圆柱,不符合题意,应舍去。(2)如果容器内的水升高后淹没放入的金属圆柱,
根据题意,得
π · 32 · x= π · 32×15+ π ·22×18解这个方程,得
x=23
23-15=8所以,容器内的水升高8厘米。小结:说说列方程解应用题的一半步骤:列一元一次方程解应用题的一般步骤:
1、分析题意,找出等量关系,分析题中数量及其关系,用字母(例如x),表示问题里的未知数.
2、用代数式表示有关的量.
3、根据等量关系列出方程.
4、解方程,求出未知数的值.
5、检验求得的值是否正确和符合实际情形,并写出答案.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
