5.1.1基本计数原理 教学设计(表格式)
文档属性
| 名称 | 5.1.1基本计数原理 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 353.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-25 19:44:28 | ||
图片预览


文档简介
教学设计
课 题 5.1.1 基本计数原理
课时安排 课前准备 翻页笔、课件、多媒体
教材内容 分 析 教材以选择交通工具、聚会服装搭配这两个学生非常熟悉的生活情境为问题,先通过分析列出解决问题的步骤,再抽象概括出分类加法计数原理和分步乘法计数原理的内容.情境的选择不求新鲜,但求熟悉,这种熟悉能引起学生对这些问题的思考,联想更多的生活经验,加深对计数原理的理解.
设计理念 先弄清楚要完成的事,再看是一步即可完成还是几步方可完成.前者是用分类加法计数原理,后者是用分步乘法计数原理.如果是使用分类加法计数原理解决问题,关系到正确分类,先明确一个分类标准,然后对完成这件事的所有方法进行分类,使完成这件事的每一种方法都属于某一类;如果是用分步乘法计数原理解决问题,关系到正确分步,先明确一个分步的标准,然后梳理出完成这件事的每一步的方法.
学情分析 “初步”主要表现在以下两个方面:(1)例题给出的解题步骤非常详尽,列出了每一类、每一步的情况,文字语言表达和符号表达应有尽有,这是初学者初步应用计数原理解决问题时所必需的;(2)例题、练习和习题的数量都不多,而且难度不大,其目的是让学生初步感受分类、分步的特征即可,在后面知识的学习过程中,都要用到这两个计数原理.如此的内容安排使学生有足够的时间和空间认识和理解这两个原理,学会应用这两个原理去思考相关问题
教学目标 1.理解基本计数原理,能正确区分“类”和“步”,掌握分类加法计数原理和分步乘法计数原理的区别与联系; 2.能运用两个计数原理解决一些简单的实际问题.
教学重难点 重点:理解基本计数原理. 难点:正确选择加法原理或者乘法原理解决问题.
教学过程
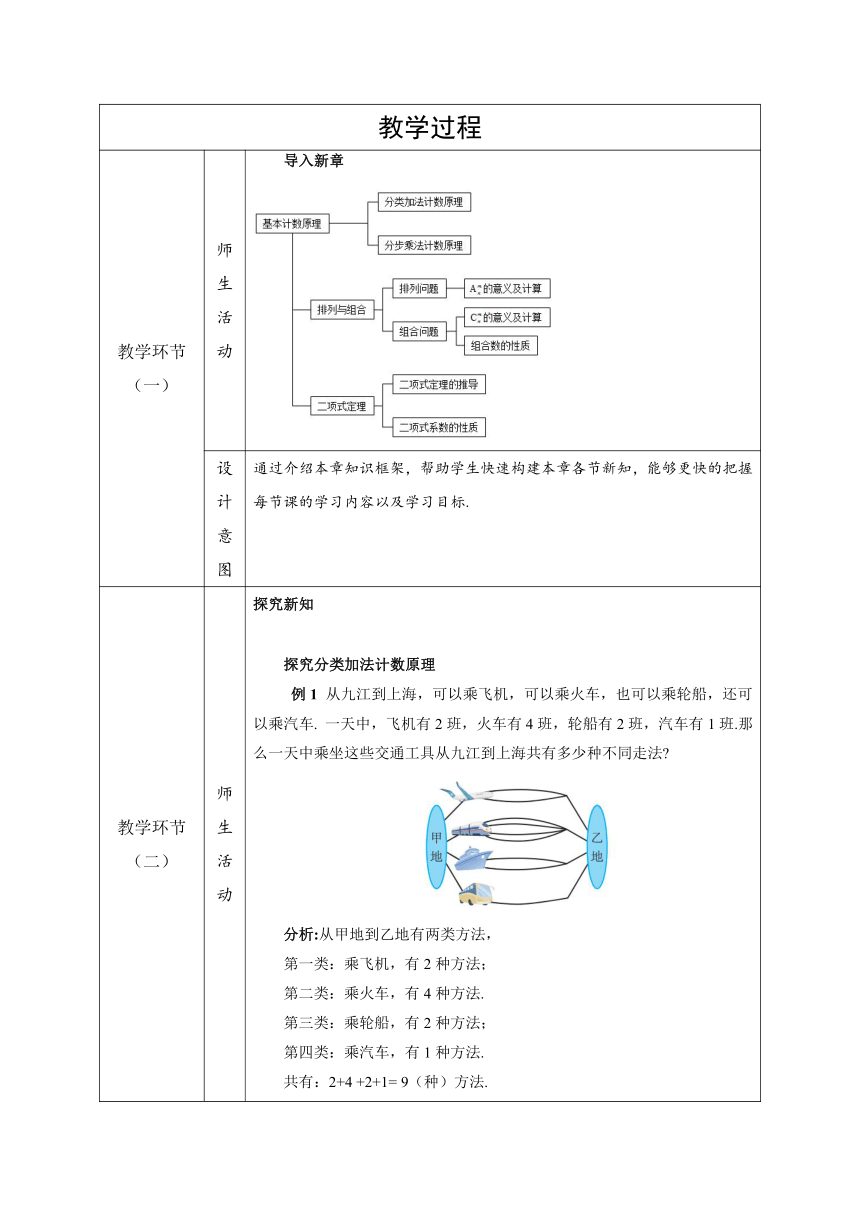
教学环节(一) 师生活动 导入新章
设计意图 通过介绍本章知识框架,帮助学生快速构建本章各节新知,能够更快的把握每节课的学习内容以及学习目标.
教学环节(二) 师生活动 探究新知 探究分类加法计数原理 例1 从九江到上海,可以乘飞机,可以乘火车,也可以乘轮船,还可以乘汽车. 一天中,飞机有2班,火车有4班,轮船有2班,汽车有1班.那么一天中乘坐这些交通工具从九江到上海共有多少种不同走法 分析:从甲地到乙地有两类方法, 第一类:乘飞机,有2种方法; 第二类:乘火车,有4种方法. 第三类:乘轮船,有2种方法; 第四类:乘汽车,有1种方法. 共有:2+4 +2+1= 9(种)方法. 问题3:你能由前两个例子归纳出解决问题的一般步骤吗? 解决上面问题的一般步骤: 分类,类与类不相交; 求每一类的方法数; 总方法数就是各类方法数之和 问题4:“不同方法”与“完成这件事”有什么关系? 分析:“不同方法”都能独立“完成这件事”,不依赖“其他方法”. 分类加法计数原理:完成一件事,有n类不同方案.在第1类方案中有种不同的方法,在第2类方案中有 种不同的方法,……,在第n类方法中有种不同的方法,则完成这件事共有种不同的方法. 归纳:分类加法计数原理特点 (1)各类方案之间相互独立,都能独立的完成这件事,要计算方法种数,只需将各类方法数相加; (2)要先根据具体的问题确定一个分类标准,在分类标准下进行分类,然后对每类方法计数. 设计意图:通过问题、归纳、操作确认、解释说明等环节,得出分类加法计数原理. 探究分步乘法计数原理 例2 春节到了,桂磊同学要与父母一起参加家庭聚会. (1)他有3件不同的上衣,4条不同的裤子,如果把1件上衣和1条裤子看作一种搭配方法,那么共有多少种搭配方法? 分析:我们先看裤子的选择方法数,有4条不同的裤子,则有4种选择方法;每一条裤子对应三件不同的上衣. 因此,根据分类加法计数原理,共有N=3+3+3+3=3×4=12种搭配方法. 问题2:(2)他还有5双不同的鞋子,如果把1件上衣、1条裤子和1双鞋子看作一种搭配方法,那么共有多少种搭配方法? 分析: 由题意知还有5双不同的鞋子,且每一双鞋子对应的裤子和上衣的搭配方法有12种,如图 因此,根据分类加法计数原理,共有N=12+12+12+12+12=12×5=3×4×5=60种搭配方法.
设计意图 设计在该环节的技术应用是否合理。同样需要考虑到技术应用是否能满足教学、是否能创新教学环节、是否符合学生学情等一些列问题。 列举熟悉的、简单的问题,使学生在情感上接受分步计数的方式.借助具体问题,使学生理解分步乘法计数原理;通过设问,加深学生对原理的理解.
教学环节 (三) 师生活动 应用举例 例3 从去往西递宏村研学的大巴上的3名老师、16名男生和14名女生中选人表演节目. (1)若只需1名参加,共有多少种选法? (2)若需教师、男学生、女学生各1名参加,共有多少种选法? 分析:(1)要完成的一件事是“选一名人员参加活动”,可以按照性别分类完成这件事; (2)要完成的一件事是“在教师、男学生、女学生各1名参加活动”,可以分步骤解决这件事. 解:(1)只要选出1名就可以完成这件事,而选出的1名有3种不同类型,即教师、男学生或女学生,因此要分3类相加: 第1类,选出的是教师,有3种选法; 第2类,选出的是男学生,有16种选法; 第3类,选出的是女学生,有14种选法. 根据分类加法计数原理,共有N=3+16+14=33种选法. (2)完成这件事,需要分别选出1名教师、1名男学生和1名女学生,可以先选教师,再选男学生,最后选女学生,因此要分3步相乘: 第1步,选1名教师,有3种选法; 第2步,选1名男学生,有16种选法; 第3步,选1名女学生,有14种选法. 根据分步乘法计数原理,共有N=3×16×14=672种选法.
设计意图 如上思考,建议要充分考虑到“恰当的时机使用恰当的技术”的问题。 学以致用.巩固对两个原理的理解;通过对比两个原理以及不同的解题思路让学生体会到两个计数原理在实际生活中的应用.
教学环节 (四) 师生活动 课堂练习 1.有三个袋子,分别装有不同编号的红色小球6个,白色小球5个,黄色小球4个.若从三个袋子中任取1个小球,有________种不同的取法. 2.一种号码锁有4个拨号盘,每个拨号盘上有从0到9共十个数字,这4个拨号盘可以组成多少个四位数的号码(各位上的数字允许重复) 参考答案: 1.15种 解析:有三类不同方案: 第一类,从第1个袋子中任取1个红色小球,有6种不同的取法; 第二类,从第2个袋子中任取1个白色小球,有5种不同的取法; 第三类,从第3个袋子中任取1个黄色小球,有4种不同的取法. 其中,从这三个袋子的任意一个袋子中取1个小球都能独立地完成“任取1个小球”这件事,根据分类加法计数原理,不同的取法共有6+5+4=15种. 2.10000个 解析:按从左到右的顺序拨号可以分四步完成: 第一步,有10种拨号方式,所以 1=10; 第二步,有10种拨号方式,所以 2=10; 第三步,有10种拨号方式,所以 3=10; 第四步,有10种拨号方式,所以 4=10. 根据分步乘法计数原理,共可以组成 =10×10×10×10=10 000个四位数的号码. 思考题:将红、黄、绿、黑四种颜色涂在如图所示的五个区域中,若要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?
设计意图 此题要让学生注意关键词的含义,审题时明确干什么事非常重要;对象选择不同,采用的计数方法也会不同. 拔高爱思考的部分优秀生,防止有学生吃不饱的状况;承接下一节知识内容,为下一节知识能力的习得作铺垫。
教学环节 (五) 师生活动 课堂小结 使用两个原理的原则 使用两个原理解题时,一定要从“分类”“分步”的角度入手. “分类”是对于较复杂应用问题的元素分成互相排斥的几类,逐类解决,用分类加法计数原理; “分步”就是把问题分化为几个互相关联的步骤,然后逐步解决,这时可用分步乘法计数原理. 应用两个计数原理计数的四个步骤 (1)明确完成的这件事是什么. (2)思考如何完成这件事. (3)判断它属于分类还是分步,是先分类后分步,还是先分步后分类. (4)选择计数原理进行计算.
设计意图 引导学生完成课堂小结,梳理知识、方法、体会.
板书设计
教学反思 数字应用基本达到预期效果,帮助学生理解,激发学习兴趣。需要改进的地方,视频和情境设置,需要寻找合适的素材,课件的制作需要更多时间和技术的支持。
课 题 5.1.1 基本计数原理
课时安排 课前准备 翻页笔、课件、多媒体
教材内容 分 析 教材以选择交通工具、聚会服装搭配这两个学生非常熟悉的生活情境为问题,先通过分析列出解决问题的步骤,再抽象概括出分类加法计数原理和分步乘法计数原理的内容.情境的选择不求新鲜,但求熟悉,这种熟悉能引起学生对这些问题的思考,联想更多的生活经验,加深对计数原理的理解.
设计理念 先弄清楚要完成的事,再看是一步即可完成还是几步方可完成.前者是用分类加法计数原理,后者是用分步乘法计数原理.如果是使用分类加法计数原理解决问题,关系到正确分类,先明确一个分类标准,然后对完成这件事的所有方法进行分类,使完成这件事的每一种方法都属于某一类;如果是用分步乘法计数原理解决问题,关系到正确分步,先明确一个分步的标准,然后梳理出完成这件事的每一步的方法.
学情分析 “初步”主要表现在以下两个方面:(1)例题给出的解题步骤非常详尽,列出了每一类、每一步的情况,文字语言表达和符号表达应有尽有,这是初学者初步应用计数原理解决问题时所必需的;(2)例题、练习和习题的数量都不多,而且难度不大,其目的是让学生初步感受分类、分步的特征即可,在后面知识的学习过程中,都要用到这两个计数原理.如此的内容安排使学生有足够的时间和空间认识和理解这两个原理,学会应用这两个原理去思考相关问题
教学目标 1.理解基本计数原理,能正确区分“类”和“步”,掌握分类加法计数原理和分步乘法计数原理的区别与联系; 2.能运用两个计数原理解决一些简单的实际问题.
教学重难点 重点:理解基本计数原理. 难点:正确选择加法原理或者乘法原理解决问题.
教学过程
教学环节(一) 师生活动 导入新章
设计意图 通过介绍本章知识框架,帮助学生快速构建本章各节新知,能够更快的把握每节课的学习内容以及学习目标.
教学环节(二) 师生活动 探究新知 探究分类加法计数原理 例1 从九江到上海,可以乘飞机,可以乘火车,也可以乘轮船,还可以乘汽车. 一天中,飞机有2班,火车有4班,轮船有2班,汽车有1班.那么一天中乘坐这些交通工具从九江到上海共有多少种不同走法 分析:从甲地到乙地有两类方法, 第一类:乘飞机,有2种方法; 第二类:乘火车,有4种方法. 第三类:乘轮船,有2种方法; 第四类:乘汽车,有1种方法. 共有:2+4 +2+1= 9(种)方法. 问题3:你能由前两个例子归纳出解决问题的一般步骤吗? 解决上面问题的一般步骤: 分类,类与类不相交; 求每一类的方法数; 总方法数就是各类方法数之和 问题4:“不同方法”与“完成这件事”有什么关系? 分析:“不同方法”都能独立“完成这件事”,不依赖“其他方法”. 分类加法计数原理:完成一件事,有n类不同方案.在第1类方案中有种不同的方法,在第2类方案中有 种不同的方法,……,在第n类方法中有种不同的方法,则完成这件事共有种不同的方法. 归纳:分类加法计数原理特点 (1)各类方案之间相互独立,都能独立的完成这件事,要计算方法种数,只需将各类方法数相加; (2)要先根据具体的问题确定一个分类标准,在分类标准下进行分类,然后对每类方法计数. 设计意图:通过问题、归纳、操作确认、解释说明等环节,得出分类加法计数原理. 探究分步乘法计数原理 例2 春节到了,桂磊同学要与父母一起参加家庭聚会. (1)他有3件不同的上衣,4条不同的裤子,如果把1件上衣和1条裤子看作一种搭配方法,那么共有多少种搭配方法? 分析:我们先看裤子的选择方法数,有4条不同的裤子,则有4种选择方法;每一条裤子对应三件不同的上衣. 因此,根据分类加法计数原理,共有N=3+3+3+3=3×4=12种搭配方法. 问题2:(2)他还有5双不同的鞋子,如果把1件上衣、1条裤子和1双鞋子看作一种搭配方法,那么共有多少种搭配方法? 分析: 由题意知还有5双不同的鞋子,且每一双鞋子对应的裤子和上衣的搭配方法有12种,如图 因此,根据分类加法计数原理,共有N=12+12+12+12+12=12×5=3×4×5=60种搭配方法.
设计意图 设计在该环节的技术应用是否合理。同样需要考虑到技术应用是否能满足教学、是否能创新教学环节、是否符合学生学情等一些列问题。 列举熟悉的、简单的问题,使学生在情感上接受分步计数的方式.借助具体问题,使学生理解分步乘法计数原理;通过设问,加深学生对原理的理解.
教学环节 (三) 师生活动 应用举例 例3 从去往西递宏村研学的大巴上的3名老师、16名男生和14名女生中选人表演节目. (1)若只需1名参加,共有多少种选法? (2)若需教师、男学生、女学生各1名参加,共有多少种选法? 分析:(1)要完成的一件事是“选一名人员参加活动”,可以按照性别分类完成这件事; (2)要完成的一件事是“在教师、男学生、女学生各1名参加活动”,可以分步骤解决这件事. 解:(1)只要选出1名就可以完成这件事,而选出的1名有3种不同类型,即教师、男学生或女学生,因此要分3类相加: 第1类,选出的是教师,有3种选法; 第2类,选出的是男学生,有16种选法; 第3类,选出的是女学生,有14种选法. 根据分类加法计数原理,共有N=3+16+14=33种选法. (2)完成这件事,需要分别选出1名教师、1名男学生和1名女学生,可以先选教师,再选男学生,最后选女学生,因此要分3步相乘: 第1步,选1名教师,有3种选法; 第2步,选1名男学生,有16种选法; 第3步,选1名女学生,有14种选法. 根据分步乘法计数原理,共有N=3×16×14=672种选法.
设计意图 如上思考,建议要充分考虑到“恰当的时机使用恰当的技术”的问题。 学以致用.巩固对两个原理的理解;通过对比两个原理以及不同的解题思路让学生体会到两个计数原理在实际生活中的应用.
教学环节 (四) 师生活动 课堂练习 1.有三个袋子,分别装有不同编号的红色小球6个,白色小球5个,黄色小球4个.若从三个袋子中任取1个小球,有________种不同的取法. 2.一种号码锁有4个拨号盘,每个拨号盘上有从0到9共十个数字,这4个拨号盘可以组成多少个四位数的号码(各位上的数字允许重复) 参考答案: 1.15种 解析:有三类不同方案: 第一类,从第1个袋子中任取1个红色小球,有6种不同的取法; 第二类,从第2个袋子中任取1个白色小球,有5种不同的取法; 第三类,从第3个袋子中任取1个黄色小球,有4种不同的取法. 其中,从这三个袋子的任意一个袋子中取1个小球都能独立地完成“任取1个小球”这件事,根据分类加法计数原理,不同的取法共有6+5+4=15种. 2.10000个 解析:按从左到右的顺序拨号可以分四步完成: 第一步,有10种拨号方式,所以 1=10; 第二步,有10种拨号方式,所以 2=10; 第三步,有10种拨号方式,所以 3=10; 第四步,有10种拨号方式,所以 4=10. 根据分步乘法计数原理,共可以组成 =10×10×10×10=10 000个四位数的号码. 思考题:将红、黄、绿、黑四种颜色涂在如图所示的五个区域中,若要求相邻的两个区域的颜色都不相同,则有多少种不同的涂色方法?
设计意图 此题要让学生注意关键词的含义,审题时明确干什么事非常重要;对象选择不同,采用的计数方法也会不同. 拔高爱思考的部分优秀生,防止有学生吃不饱的状况;承接下一节知识内容,为下一节知识能力的习得作铺垫。
教学环节 (五) 师生活动 课堂小结 使用两个原理的原则 使用两个原理解题时,一定要从“分类”“分步”的角度入手. “分类”是对于较复杂应用问题的元素分成互相排斥的几类,逐类解决,用分类加法计数原理; “分步”就是把问题分化为几个互相关联的步骤,然后逐步解决,这时可用分步乘法计数原理. 应用两个计数原理计数的四个步骤 (1)明确完成的这件事是什么. (2)思考如何完成这件事. (3)判断它属于分类还是分步,是先分类后分步,还是先分步后分类. (4)选择计数原理进行计算.
设计意图 引导学生完成课堂小结,梳理知识、方法、体会.
板书设计
教学反思 数字应用基本达到预期效果,帮助学生理解,激发学习兴趣。需要改进的地方,视频和情境设置,需要寻找合适的素材,课件的制作需要更多时间和技术的支持。
同课章节目录
