山西省2024年中考考试数学真题试卷(含答案)
文档属性
| 名称 | 山西省2024年中考考试数学真题试卷(含答案) | 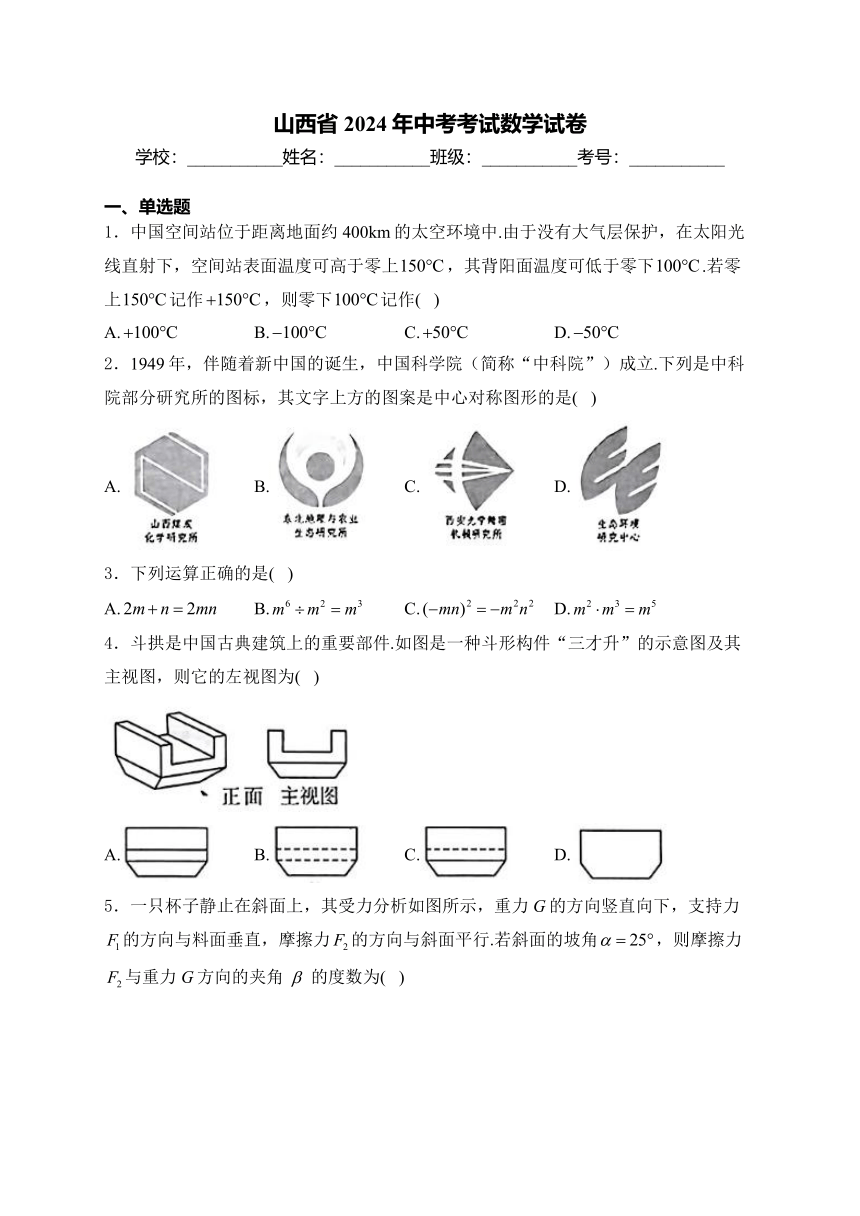 | |
| 格式 | docx | ||
| 文件大小 | 777.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 08:48:26 | ||
图片预览





文档简介
山西省2024年中考考试数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.中国空间站位于距离地面约400km的太空环境中.由于没有大气层保护,在太阳光线直射下,空间站表面温度可高于零上,其背阳面温度可低于零下.若零上记作,则零下记作( )
A. B. C. D.
2.1949年,伴随着新中国的诞生,中国科学院(简称“中科院”)成立.下列是中科院部分研究所的图标,其文字上方的图案是中心对称图形的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.斗拱是中国古典建筑上的重要部件.如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )
A. B. C. D.
5.一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力的方向与料面垂直,摩擦力的方向与斜面平行.若斜面的坡角,则摩擦力与重力G方向的夹角的度数为( )
A. B. C. D.
6.已知点,都在正比例函数的图象上,若,则与的大小关系是( )
A. B. C. D.
7.如图,已知,以AB为直径的交BC于点D,与AC相切于点A,连接OD.若,则的度数为( )
A. B. C. D.
8.一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球恰好有一个红球的概率是( )
A. B. C. D.
9.生物学研究表明,某种蛇在一定生长阶段.其体长是尾长的一次函数,部分数据如下表所示,则y与x之间的关系式为( )
尾长 6 8 10
体长 45.5 60.5 75.5
A. B. C. D.
10.在四边形中,点E,F,G,H分别是边,,,的中点,EG,FH交于点O.若四边形ABCD的对角线相等,则线段EG与FH一定满足的关系为( )
A.互相垂直平分 B.互相平分且相等
C.互相垂直且相等 D.互相垂直平分且相等
二、填空题
11.比较大小:________2(填“>”“<”或“=”).
12.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分制线的端点A,B分别在习字格的边MN,PQ上,且,“晋”字的笔画“、”的位置在AB的黄金分割点C处,且.若,则BC的长为________(结果保留根号).
13.机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度是载重后总质量的反比例函数.已知一款机器狗载重后总质量时,它的最快移动速度;当其载重后总质量时,它的最快移动速度________.
14.如图1是小区围墙上的花窗,其形状是扇形的一部分,图2是其几何示意图(阴影部分为花窗).通过测量得到扇形AOB的圆心角为,,点C,D分别为OA,OB的中点,则花窗的面积为________.
15.如图,在中,AC为对角线,于点E,点F是AE延长线上一点,且,线段,的延长线交于点G.若,,,则BG的长为________.
三、解答题
16.(1)计算:;
(2)化简:.
17.为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为540元/个,干粉灭火器的单价为380元/个.若学校购买这两种灭火器的总价不超过21000元则最多可购买这种型号的水基灭火器多少个?
18.为激发青少年崇尚科学、探索木知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图,
数据分析:小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:________,________,________.
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).
19.当下电子产品更新换代速度加快,废旧智能手机数量不断增加,科学处理废旧智能手机,既可减少环境污染,还可回收其中的可利用资源据研究,从每吨废旧智能手机中能提炼出的白银比黄金多760克.已知从2.5吨废旧智能手机中提炼出的黄金,与从0.6吨废旧智能手机中提炼出的白银克数相等.求从每吨废旧智能手机中能提炼出黄金与白银各多少克.
20.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.
数据采集:如下图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离.航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角;然后沿CN方向继续飞行,飞行方向与水平线的夹角,当到达点A正上方的点E处时,测得米;…
数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计 纪念碑顶部点A到地面的距离AB的长(结果精确到1米.参考数据:,,,,,).
21.阅读与思考下面是博学小组研究性学习报告的部分内容,请认真阅读”并完成相应任务.
关于“等边半正多边形”的研究报告博学小组研究对象:等边半正多边形研究思路:类比三角形、四边形,按“概念一性质一判定”的路径,由一般到特殊进行研究研究方法:观察(测量、实验)一猜想一推理证明研究内容: 【一般概念】对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形,如图1,我们学习过的菱形(正方形除外)就是等边半正四边形.类似地,还有等边半正六边形、等边半正八边形… 【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下: 概念理解析:如图2,如果六边形ABCDEF是等边半正六边形,那么,,,且. 性质探索:根据定义,探索等边半正六边形的性质,得到如下结论: 内角:等边半正六边形相邻两个内角的和为▲°, 对角线:…
任务:
(1)直接写出研究报告中“▲”处空缺的内容;_________.
(2)如图3,六边形ABCDEF是等边半正六边形.连接对角线AD,猜想
与的数量关系,并说明理由;
(3)如图4,已知是正三角形、是它的外接圆.请在图4中作一个等边半正六边形ABCDEF(要求:尺规作图、保留作图痕迹,不写作法).
22.综合与实践问题情境:如图1,矩形MNKL是学校花园的示意图,其中一个花坛的轮廓可近似看成由抛物线的一部分与线段AB组成的封闭图形,点A,B在矩形的边MN上.现要对该花坛内种植区域进行划分,以种植不同花卉,学校而向全体同学征集设计方案,方案设计:如图2,米,AB的垂直平分线与抛物线交于点P,与AB交于点O,点P是抛物线的顶点,且米,欣欣设计的方案如下:
第一步:在线段OP上确定点C,使.用篱笆沿线段AC,BC分隔出区域,种植串串红;
第二步:在线段CP上取点F(不与C,P重合),过点F作AB的平行线,交抛物线于点D,E.用篱笆沿DE,CF将线段AC,BC与抛物线围成的区域分隔成三部分,分别种植不同花色的月季.
方案实施:学校采用了欣欣的方案、在完成第一步区域的分隔后,发现仅剩6米篱笆材料.若要在第二步分隔中恰好用完6米材料,需确定DE与CF的长.为此,欣欣在图2中以AB所在直线为x轴,OP所在直线为y轴建立平面直角坐标系.请按照她的方法解决问题:
(1)在图2中画出坐标系,并求抛物线的函数表达式;
(2)求6米材料恰好用完时DE与CF的长;
(3)种植区域分隔完成后,欣欣又想用灯带对该花坛进行装饰,计划将灯带围成一个矩形.她尝试借助图2设计矩形四个顶点的位置,其中两个顶点在抛物线上,另外两个顶点分别在线段AC,BC上.直接写出符合设计要求的矩形周长的最大值.
23.综合与探究
问题情境:如图1,四边形ABCD是菱形,过点A作于点E,过点C作于点F.
猜想证明:(1)判断四边形AECF的形状,并说明理由;
深入探究:(2)将图1中的绕点A逆时针旋转,得到,点E,B的对应点分别为点G,H.
①如图2,当线段AH经过点C时,GH所在直线分别与线段AD,CD交于点M,N.猜想线段CH与MD的数量关系,并说明理由;
②当直线GH与直线CD垂直时,直线GH分别与直线AD,CD交于点M,N,直线AH与线段CD交于点.若,直接写出四边形AMNQ的面积.
参考答案
1.答案:B
解析:
2.答案:A
解析:
3.答案:D
解析:
4.答案:C
解析:
5.答案:C
解析:
6.答案:B
解析:
7.答案:D
解析:
8.答案:B
解析:
9.答案:A
解析:
10.答案:A
解析:
11.答案:>
解析:
12.答案:
解析:
13.答案:4
解析:
14.答案:
解析:
15.答案:
解析:
16.答案:(1)-10
(2)
解析:(1)原式
(2)原式
.
17.答案:最多可购买这种型号的水基灭火器12个
解析:设可购买这种型号的水基灭火器x个,
根据题意,得.
得.
因为x为整数,且x取最大值,所以.
答:最多可购买这种型号的水基灭火器12个.
18.答案:(1)7.5;7;25%
(2)见解析
解析:(1)7.5;7;25%.
(2)答案不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,所以从优秀率的角度看,甲组成绩比乙组好;②虽然甲、乙两组成绩的平均数相等,但甲组成绩的方差为4.48,高于乙组成绩的方差0.73,所以从方差的角度看,乙组成绩更整齐;③甲组成绩的中位数为7.5分,高于乙组成绩的中位数7分,所以从中位数的角度看,甲组成绩比乙组好,等.因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
19.答案:从每吨废旧智能手机中能提炼出黄金210克,白银1000克
解析:设从每吨废旧智能手机中能提炼出黄金x克,白银y克.
根据题意,得.
解得.
答:从每吨废旧智能手机中能提炼出黄金210克,白银1000克.
20.答案:27米
解析:延长CD交AB于点H.
由题意得,四边形CMBH为矩形.
.
在中,,,
,,
在中,,,
,.
设.
,,.
解得.
(米)
答:点A到地面的距离AB的长约为27米.
21.答案:(1)240
(2)见解析
(3)见解析
解析:(1)240.
(2).
理由如下:连接BD,FD.
六边形ABCDEF是等边半正六边形.
,.
,.
在与中,
,.
(3)答案不唯一,例如:
如图,六边形ABCDEF即为所求.
22.答案:(1)
(2)DE的长为4米,CF的长为2米
(3)
解析:(1)建立如图所示的平面直角坐标系.
所在直线是AB的垂直平分线,且,
.
点B的坐标为.
,点P的坐标为.
点P是抛物线的顶点,
设抛物线的函数表达式为.
点在抛物线上,
.解得.
抛物线的函数表达式为.
(2)点D,E在抛物线上,
设点E的坐标为.
,交y轴于点F,
,,.
在中,,,
.
.
根据题意,得,
.
解,得,(不符合题意,舍去),
.,.
答:DE的长为4米,CF的长为2米.
(3).
23.答案:(1)矩形
(2)①;②或
解析:(1)四边形AECF为矩形.
理由如下:,,
,.
四边形ABCD为菱形,,.
.
四边形AECF为矩形.
(2)①.
理由如下:
证法一:四边形ABCD为菱形,,.
旋转得到,
,.
,.
,.
,.
.
证法二:如图,连接HD.
四边形ABCD为菱形,,.
旋转得到,
,.
,.
.
.
.
,.
.
②或.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.中国空间站位于距离地面约400km的太空环境中.由于没有大气层保护,在太阳光线直射下,空间站表面温度可高于零上,其背阳面温度可低于零下.若零上记作,则零下记作( )
A. B. C. D.
2.1949年,伴随着新中国的诞生,中国科学院(简称“中科院”)成立.下列是中科院部分研究所的图标,其文字上方的图案是中心对称图形的是( )
A. B. C. D.
3.下列运算正确的是( )
A. B. C. D.
4.斗拱是中国古典建筑上的重要部件.如图是一种斗形构件“三才升”的示意图及其主视图,则它的左视图为( )
A. B. C. D.
5.一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力的方向与料面垂直,摩擦力的方向与斜面平行.若斜面的坡角,则摩擦力与重力G方向的夹角的度数为( )
A. B. C. D.
6.已知点,都在正比例函数的图象上,若,则与的大小关系是( )
A. B. C. D.
7.如图,已知,以AB为直径的交BC于点D,与AC相切于点A,连接OD.若,则的度数为( )
A. B. C. D.
8.一个不透明的盒子里装有一个红球、一个白球和一个绿球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后不放回,再从中随机摸出一个球,则两次摸到的球恰好有一个红球的概率是( )
A. B. C. D.
9.生物学研究表明,某种蛇在一定生长阶段.其体长是尾长的一次函数,部分数据如下表所示,则y与x之间的关系式为( )
尾长 6 8 10
体长 45.5 60.5 75.5
A. B. C. D.
10.在四边形中,点E,F,G,H分别是边,,,的中点,EG,FH交于点O.若四边形ABCD的对角线相等,则线段EG与FH一定满足的关系为( )
A.互相垂直平分 B.互相平分且相等
C.互相垂直且相等 D.互相垂直平分且相等
二、填空题
11.比较大小:________2(填“>”“<”或“=”).
12.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分制线的端点A,B分别在习字格的边MN,PQ上,且,“晋”字的笔画“、”的位置在AB的黄金分割点C处,且.若,则BC的长为________(结果保留根号).
13.机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度是载重后总质量的反比例函数.已知一款机器狗载重后总质量时,它的最快移动速度;当其载重后总质量时,它的最快移动速度________.
14.如图1是小区围墙上的花窗,其形状是扇形的一部分,图2是其几何示意图(阴影部分为花窗).通过测量得到扇形AOB的圆心角为,,点C,D分别为OA,OB的中点,则花窗的面积为________.
15.如图,在中,AC为对角线,于点E,点F是AE延长线上一点,且,线段,的延长线交于点G.若,,,则BG的长为________.
三、解答题
16.(1)计算:;
(2)化简:.
17.为加强校园消防安全,学校计划购买某种型号的水基灭火器和干粉灭火器共50个.其中水基灭火器的单价为540元/个,干粉灭火器的单价为380元/个.若学校购买这两种灭火器的总价不超过21000元则最多可购买这种型号的水基灭火器多少个?
18.为激发青少年崇尚科学、探索木知的热情,学校开展“科学小博士”知识竞赛.各班以小组为单位组织初赛,规定满分为10分,9分及以上为优秀.
数据整理:小夏将本班甲、乙两组同学(每组8人)初赛的成绩整理成如下的统计图,
数据分析:小夏对这两个小组的成绩进行了如下分析:
平均数(分) 中位数(分) 众数(分) 方差 优秀率
甲组 7.625 a 7 4.48 37.5%
乙组 7.625 7 b 0.73 c
请认真阅读上述信息,回答下列问题:
(1)填空:________,________,________.
(2)小祺认为甲、乙两组成绩的平均数相等,因此两个组成绩一样好.小夏认为小祺的观点比较片面,请结合上表中的信息帮小夏说明理由(写出两条即可).
19.当下电子产品更新换代速度加快,废旧智能手机数量不断增加,科学处理废旧智能手机,既可减少环境污染,还可回收其中的可利用资源据研究,从每吨废旧智能手机中能提炼出的白银比黄金多760克.已知从2.5吨废旧智能手机中提炼出的黄金,与从0.6吨废旧智能手机中提炼出的白银克数相等.求从每吨废旧智能手机中能提炼出黄金与白银各多少克.
20.研学实践:为重温解放军东渡黄河“红色记忆”,学校组织研学活动.同学们来到毛主席东渡黄河纪念碑所在地,在了解相关历史背景后,利用航模搭载的3D扫描仪采集纪念碑的相关数据.
数据采集:如下图,点A是纪念碑顶部一点,AB的长表示点A到水平地面的距离.航模从纪念碑前水平地面的点M处竖直上升,飞行至距离地面20米的点C处时,测得点A的仰角;然后沿CN方向继续飞行,飞行方向与水平线的夹角,当到达点A正上方的点E处时,测得米;…
数据应用:已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计 纪念碑顶部点A到地面的距离AB的长(结果精确到1米.参考数据:,,,,,).
21.阅读与思考下面是博学小组研究性学习报告的部分内容,请认真阅读”并完成相应任务.
关于“等边半正多边形”的研究报告博学小组研究对象:等边半正多边形研究思路:类比三角形、四边形,按“概念一性质一判定”的路径,由一般到特殊进行研究研究方法:观察(测量、实验)一猜想一推理证明研究内容: 【一般概念】对于一个凸多边形(边数为偶数),若其各边都相等,且相间的角相等、相邻的角不相等,我们称这个凸多边形为等边半正多边形,如图1,我们学习过的菱形(正方形除外)就是等边半正四边形.类似地,还有等边半正六边形、等边半正八边形… 【特例研究】根据等边半正多边形的定义,对等边半正六边形研究如下: 概念理解析:如图2,如果六边形ABCDEF是等边半正六边形,那么,,,且. 性质探索:根据定义,探索等边半正六边形的性质,得到如下结论: 内角:等边半正六边形相邻两个内角的和为▲°, 对角线:…
任务:
(1)直接写出研究报告中“▲”处空缺的内容;_________.
(2)如图3,六边形ABCDEF是等边半正六边形.连接对角线AD,猜想
与的数量关系,并说明理由;
(3)如图4,已知是正三角形、是它的外接圆.请在图4中作一个等边半正六边形ABCDEF(要求:尺规作图、保留作图痕迹,不写作法).
22.综合与实践问题情境:如图1,矩形MNKL是学校花园的示意图,其中一个花坛的轮廓可近似看成由抛物线的一部分与线段AB组成的封闭图形,点A,B在矩形的边MN上.现要对该花坛内种植区域进行划分,以种植不同花卉,学校而向全体同学征集设计方案,方案设计:如图2,米,AB的垂直平分线与抛物线交于点P,与AB交于点O,点P是抛物线的顶点,且米,欣欣设计的方案如下:
第一步:在线段OP上确定点C,使.用篱笆沿线段AC,BC分隔出区域,种植串串红;
第二步:在线段CP上取点F(不与C,P重合),过点F作AB的平行线,交抛物线于点D,E.用篱笆沿DE,CF将线段AC,BC与抛物线围成的区域分隔成三部分,分别种植不同花色的月季.
方案实施:学校采用了欣欣的方案、在完成第一步区域的分隔后,发现仅剩6米篱笆材料.若要在第二步分隔中恰好用完6米材料,需确定DE与CF的长.为此,欣欣在图2中以AB所在直线为x轴,OP所在直线为y轴建立平面直角坐标系.请按照她的方法解决问题:
(1)在图2中画出坐标系,并求抛物线的函数表达式;
(2)求6米材料恰好用完时DE与CF的长;
(3)种植区域分隔完成后,欣欣又想用灯带对该花坛进行装饰,计划将灯带围成一个矩形.她尝试借助图2设计矩形四个顶点的位置,其中两个顶点在抛物线上,另外两个顶点分别在线段AC,BC上.直接写出符合设计要求的矩形周长的最大值.
23.综合与探究
问题情境:如图1,四边形ABCD是菱形,过点A作于点E,过点C作于点F.
猜想证明:(1)判断四边形AECF的形状,并说明理由;
深入探究:(2)将图1中的绕点A逆时针旋转,得到,点E,B的对应点分别为点G,H.
①如图2,当线段AH经过点C时,GH所在直线分别与线段AD,CD交于点M,N.猜想线段CH与MD的数量关系,并说明理由;
②当直线GH与直线CD垂直时,直线GH分别与直线AD,CD交于点M,N,直线AH与线段CD交于点.若,直接写出四边形AMNQ的面积.
参考答案
1.答案:B
解析:
2.答案:A
解析:
3.答案:D
解析:
4.答案:C
解析:
5.答案:C
解析:
6.答案:B
解析:
7.答案:D
解析:
8.答案:B
解析:
9.答案:A
解析:
10.答案:A
解析:
11.答案:>
解析:
12.答案:
解析:
13.答案:4
解析:
14.答案:
解析:
15.答案:
解析:
16.答案:(1)-10
(2)
解析:(1)原式
(2)原式
.
17.答案:最多可购买这种型号的水基灭火器12个
解析:设可购买这种型号的水基灭火器x个,
根据题意,得.
得.
因为x为整数,且x取最大值,所以.
答:最多可购买这种型号的水基灭火器12个.
18.答案:(1)7.5;7;25%
(2)见解析
解析:(1)7.5;7;25%.
(2)答案不唯一,例如:①甲组成绩的优秀率为37.5%,高于乙组成绩的优秀率25%,所以从优秀率的角度看,甲组成绩比乙组好;②虽然甲、乙两组成绩的平均数相等,但甲组成绩的方差为4.48,高于乙组成绩的方差0.73,所以从方差的角度看,乙组成绩更整齐;③甲组成绩的中位数为7.5分,高于乙组成绩的中位数7分,所以从中位数的角度看,甲组成绩比乙组好,等.因此不能仅从平均数的角度说明两组成绩一样好,可见,小祺的观点比较片面.
19.答案:从每吨废旧智能手机中能提炼出黄金210克,白银1000克
解析:设从每吨废旧智能手机中能提炼出黄金x克,白银y克.
根据题意,得.
解得.
答:从每吨废旧智能手机中能提炼出黄金210克,白银1000克.
20.答案:27米
解析:延长CD交AB于点H.
由题意得,四边形CMBH为矩形.
.
在中,,,
,,
在中,,,
,.
设.
,,.
解得.
(米)
答:点A到地面的距离AB的长约为27米.
21.答案:(1)240
(2)见解析
(3)见解析
解析:(1)240.
(2).
理由如下:连接BD,FD.
六边形ABCDEF是等边半正六边形.
,.
,.
在与中,
,.
(3)答案不唯一,例如:
如图,六边形ABCDEF即为所求.
22.答案:(1)
(2)DE的长为4米,CF的长为2米
(3)
解析:(1)建立如图所示的平面直角坐标系.
所在直线是AB的垂直平分线,且,
.
点B的坐标为.
,点P的坐标为.
点P是抛物线的顶点,
设抛物线的函数表达式为.
点在抛物线上,
.解得.
抛物线的函数表达式为.
(2)点D,E在抛物线上,
设点E的坐标为.
,交y轴于点F,
,,.
在中,,,
.
.
根据题意,得,
.
解,得,(不符合题意,舍去),
.,.
答:DE的长为4米,CF的长为2米.
(3).
23.答案:(1)矩形
(2)①;②或
解析:(1)四边形AECF为矩形.
理由如下:,,
,.
四边形ABCD为菱形,,.
.
四边形AECF为矩形.
(2)①.
理由如下:
证法一:四边形ABCD为菱形,,.
旋转得到,
,.
,.
,.
,.
.
证法二:如图,连接HD.
四边形ABCD为菱形,,.
旋转得到,
,.
,.
.
.
.
,.
.
②或.
同课章节目录
