数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算 课件(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册1.1.2空间向量的数量积运算 课件(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 15:01:08 | ||
图片预览





文档简介
(共17张PPT)
1.1.2 空间向量的数量积运算
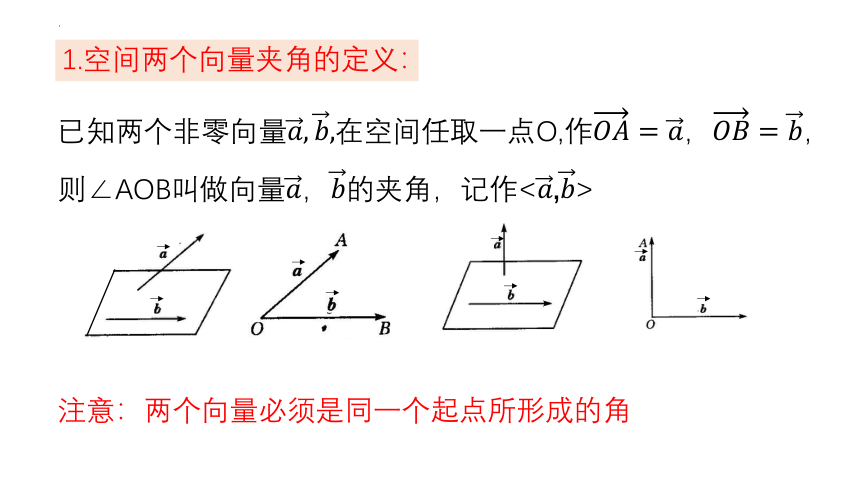
1.空间两个向量夹角的定义:
已知两个非零向量在空间任取一点O,作,,则∠AOB叫做向量的夹角,记作<,>
注意:两个向量必须是同一个起点所形成的角
2.空间两个向量夹角的取值范围:
通常规定0≤ <,> ≤
(1)当,同向时,<,>=0
当,反向时,<,>=
(2)两个向量的夹角是唯一确定的,且<,>= <>
(3)若<,>=,则向量,互相垂直,记作
想一想:
空间向量的夹角与两条相交直线的夹角相同吗?
答:不相同
两条相交直线的夹角是指这两条直线所成的锐角或直角,
即取值范围是(0°,90°];
而向量的夹角必须是同起点,其取值范围[0°,180°]
3.空间两个向量的数量积:
已知两个非零向量,则| |cos<,>叫做,的
数量积,记作,即= | |cos<,>
特别地: (1)零向量与任意向量的数量积为0.
(2)=0
(=
注:两个向量的数量积是数量,而不是向量.
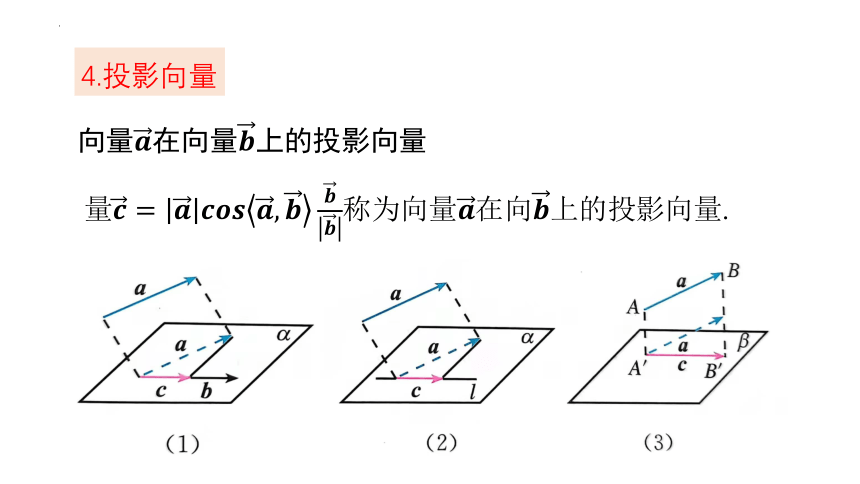
向量在向量上的投影向量
量称为向量在向上的投影向量.
4.投影向量
5.空间向量数量积的运算律:
注意:
(1)数量积不满足结合律即()
(1)( =(
(2)=
(3)(+
(2)=
(3)=0
对于空间向量下列命题成立吗
①若 ,则
②若 ,则
③
A
B
C
D
A1
B1
C1
D1
(结合律)
6.空间两个向量数量积的性质:
(1)||cos<>
(2)=0
(3)
(4)||
(5)cos<>=
例1如图,在平行六面体ABCD-A′B′C′D′中,AB=5,AD=3,
AA′=7,∠BAD=60°,∠BAA′=∠DAA′=45°.求:
例2 如图,m,n是平面α内的两条相交直线.如果l⊥m,l⊥n,求证:l⊥α.
【解析】 在平面α内作任意一条直线g,分别在直线l,m,n,g上取非零向量,,,.
因为直线m与n相交,所以向量,不平行.
由向量共面的充要条件可知,存在唯一的有序实数对(x,y),使=x +y .
将上式两边分别与向量作数量积运算,得· =x · +y · .
因为·=0, ·=0,所以·=0,所以l⊥g.
这就证明了直线l垂直于平面α内的任意一条直线,所以l⊥α.
1、已知空间向量,满足||=4,| |=8,与的夹角是150°,计算:(1)(+2)·(2- );(2)|4一2 |.
当堂训练
4.如果, 是两个夹角为60°的单位空间向量,则= + 与= -2 的夹角为 .
答案:120°
5.如图,在棱长为a的正方体ABCD-A1B1C1D1中,求异面直线BA1与AC所成的角.
1.1.2 空间向量的数量积运算
1.空间两个向量夹角的定义:
已知两个非零向量在空间任取一点O,作,,则∠AOB叫做向量的夹角,记作<,>
注意:两个向量必须是同一个起点所形成的角
2.空间两个向量夹角的取值范围:
通常规定0≤ <,> ≤
(1)当,同向时,<,>=0
当,反向时,<,>=
(2)两个向量的夹角是唯一确定的,且<,>= <>
(3)若<,>=,则向量,互相垂直,记作
想一想:
空间向量的夹角与两条相交直线的夹角相同吗?
答:不相同
两条相交直线的夹角是指这两条直线所成的锐角或直角,
即取值范围是(0°,90°];
而向量的夹角必须是同起点,其取值范围[0°,180°]
3.空间两个向量的数量积:
已知两个非零向量,则| |cos<,>叫做,的
数量积,记作,即= | |cos<,>
特别地: (1)零向量与任意向量的数量积为0.
(2)=0
(=
注:两个向量的数量积是数量,而不是向量.
向量在向量上的投影向量
量称为向量在向上的投影向量.
4.投影向量
5.空间向量数量积的运算律:
注意:
(1)数量积不满足结合律即()
(1)( =(
(2)=
(3)(+
(2)=
(3)=0
对于空间向量下列命题成立吗
①若 ,则
②若 ,则
③
A
B
C
D
A1
B1
C1
D1
(结合律)
6.空间两个向量数量积的性质:
(1)||cos<>
(2)=0
(3)
(4)||
(5)cos<>=
例1如图,在平行六面体ABCD-A′B′C′D′中,AB=5,AD=3,
AA′=7,∠BAD=60°,∠BAA′=∠DAA′=45°.求:
例2 如图,m,n是平面α内的两条相交直线.如果l⊥m,l⊥n,求证:l⊥α.
【解析】 在平面α内作任意一条直线g,分别在直线l,m,n,g上取非零向量,,,.
因为直线m与n相交,所以向量,不平行.
由向量共面的充要条件可知,存在唯一的有序实数对(x,y),使=x +y .
将上式两边分别与向量作数量积运算,得· =x · +y · .
因为·=0, ·=0,所以·=0,所以l⊥g.
这就证明了直线l垂直于平面α内的任意一条直线,所以l⊥α.
1、已知空间向量,满足||=4,| |=8,与的夹角是150°,计算:(1)(+2)·(2- );(2)|4一2 |.
当堂训练
4.如果, 是两个夹角为60°的单位空间向量,则= + 与= -2 的夹角为 .
答案:120°
5.如图,在棱长为a的正方体ABCD-A1B1C1D1中,求异面直线BA1与AC所成的角.
