2023-2024学年海南省儋州市高二下学期期末考试数学试题(含答案)
文档属性
| 名称 | 2023-2024学年海南省儋州市高二下学期期末考试数学试题(含答案) | 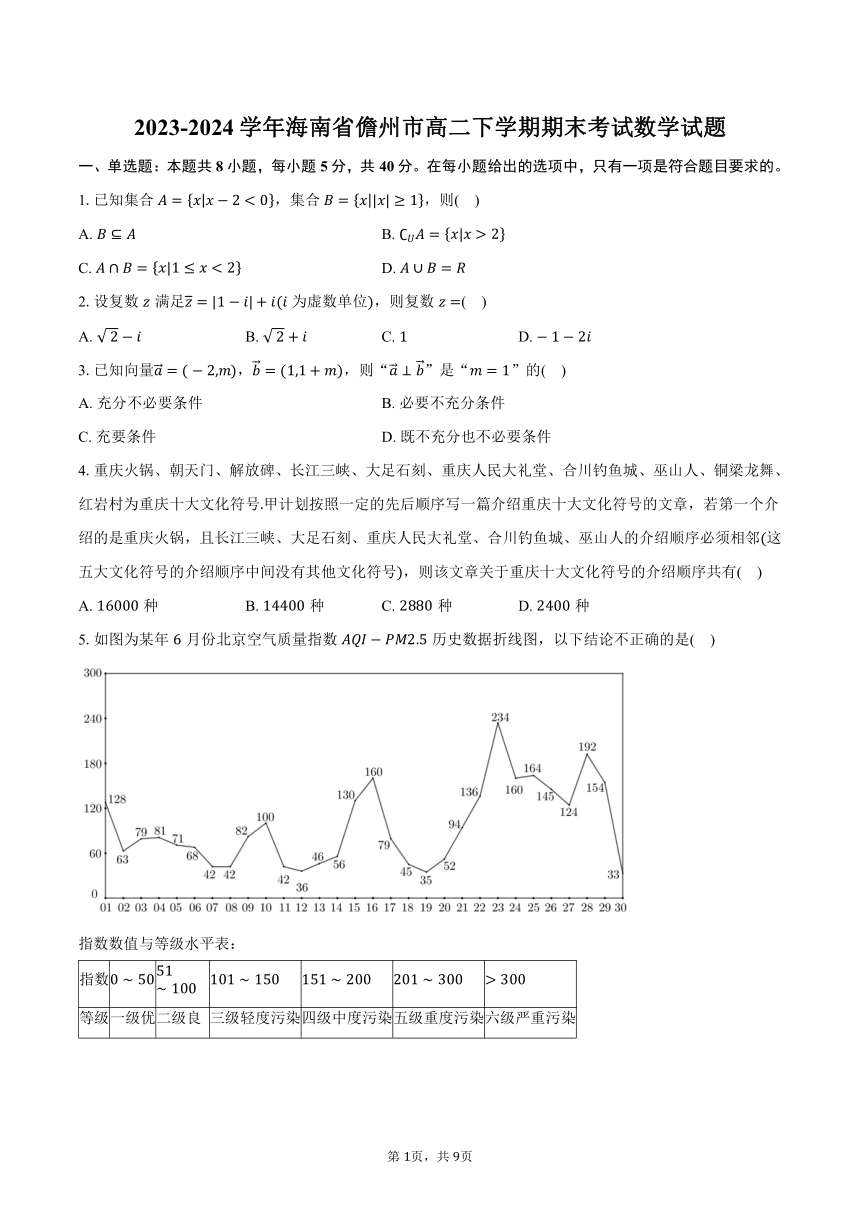 | |
| 格式 | docx | ||
| 文件大小 | 233.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 15:07:01 | ||
图片预览




文档简介
2023-2024学年海南省儋州市高二下学期期末考试数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,集合,则( )
A. B.
C. D.
2.设复数满足为虚数单位,则复数( )
A. B. C. D.
3.已知向量,,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4.重庆火锅、朝天门、解放碑、长江三峡、大足石刻、重庆人民大礼堂、合川钓鱼城、巫山人、铜梁龙舞、红岩村为重庆十大文化符号甲计划按照一定的先后顺序写一篇介绍重庆十大文化符号的文章,若第一个介绍的是重庆火锅,且长江三峡、大足石刻、重庆人民大礼堂、合川钓鱼城、巫山人的介绍顺序必须相邻这五大文化符号的介绍顺序中间没有其他文化符号,则该文章关于重庆十大文化符号的介绍顺序共有( )
A. 种 B. 种 C. 种 D. 种
5.如图为某年月份北京空气质量指数历史数据折线图,以下结论不正确的是( )
指数数值与等级水平表:
指数
等级 一级优 二级良 三级轻度污染 四级中度污染 五级重度污染 六级严重污染
A. 月份空气质量为优的天数为天
B. 月份连续天出现中度污染的概率为
C. 月份北京空气质量指数历史数据的众数为
D. 北京月至日这天的空气质量逐渐变好
6.如图,,,表示个开关,若在某段时间内它们正常工作的概率分别为,,,那么系统的可靠性为( )
A. B. C. D.
7.已知三棱锥的三条侧棱两两互相垂直,且,,,则此三棱锥的外接球的体积为( )
A. B. C. D.
8.已知,,,,则下列大小关系正确的是( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.年月日,某市物价部门对家商场的某商品一天的销售量及其价格进行调查,家商场的售价元和销售量件之间的一组数据如表所示:
售价
销售量
根据表中数据得到关于的回归直线方程是,则下列说法正确的有 .
A. B. 回归直线过点
C. 当时,的估计值为 D. 点处的随机误差为
10.下列结论正确的是( )
A. 若随机变量的方差,则
B. 若随机变量服从正态分布,且,则
C. 从装有大小、形状都相同的个红球和个白球的袋中随机取出两球,取到白球的个数记为,则
D. 若随机变量服从二项分布,则的分布列可表示为,
11.设抛物线的焦点为,是上的一个动点,则下列结论正确的是( )
A. 点到的距离比到轴的距离大
B. 点到直线的最小距离为
C. 以为直径的圆与轴相切
D. 记点在的准线上的射影为,则不可能是正三角形
三、填空题:本题共3小题,每小题5分,共15分。
12.数列中,,时,,则的通项公式是
13.若的展开式中的系数为,则展开式中所有项的二项式系数之和为 以数字作答
14.作家马伯庸小说长安十二时辰中,靖安司通过长安城内的望楼传递信息同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色此处以阴影代表紫色之间变换,从而一共可以有种不同的颜色组合,即代表种不同的信息现要求每一行、每一列上都有且只有个紫色小方格如图所示即满足要求则一共可以传递 种信息用数字作答
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知数列的前项和为,.
求;
若,求数列的前项和.
16.本小题分
设函数.
若曲线在点处的切线方程是,求的值;
求函数的单调区间及极值.
17.本小题分
如图,在三棱柱中,是边长为的等边三角形,平面平面,,,为的中点,为的中点.
求证:平面;
求二面角的正弦值.
18.本小题分
已知抛物线上一点到焦点的距离为,点到轴的距离为.
求抛物线的方程;
过的直线交抛物线于,两点,过点作轴的垂线交直线是坐标原点于,过作直线的垂线与抛物线的另一交点为,直线与交于点求
19.本小题分
为进一步加强城市建设和产业集聚效应,某市通过“两化”中的信息化和工业化之间的完美交融结合,达到了经济效益的“倍增式”发展.该市某高科技企业对某核心技术加大研发投资力度,持续构建面向未来的竞争力.现得到一组在该技术研发投入单位:亿元与收益单位:亿元的数据如下表所示:
研发投入
收益
已知可用一元线性回归模型模型拟合与的关系,求此经验回归方程;附:对于一组数据,,,,其经验回归直线的斜率和截距的最小二乘法估计公式分别为,,,,结果保留两位小数
该企业主要生产、类产品,现随机抽取类产品件、类产品件进行质量检验,已知类、类产品独立检验为合格品的概率分别为,,求在恰有件产品为合格品的条件下,类产品为合格品的概率.
答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由题意,数列满足,
当时,可得,
两式相减,可得,整理得,即,
当时,可得,解得,
所以数列是首项为,公比为的等比数列,
所以,所以.
由知,则
设,数列的前项和分别为,
则
,
两式相减得,
所以,
又由,
所以数列的前项和.
16.解:曲线在点处的切线方程是,
,
所以,,
则,
解得.
因为,,
由,解得,
当时,,函数单调递增;
当时,,函数单调递减;
当时,,函数单调递增.
此时是的极大值点,是的极小值点,
的极大值为,
的极小值为.
函数单调递增区间为和;
函数单调递减区间为.
17.证明:取中点,连接,,
,, ,
三棱柱,为的中点,, ,
,四边形为平行四边形,
.
平面,平面,
平面
连接,,
,,,
平面平面,平面平面,
平面,平面,
,,
为等边三角形,
,,
两两垂直,
以为正交基底建立如图所示的空间直角坐标系,
,,,,.
,.
设平面的一个法向量为,
取,得.
平面的一个法向量为,
,.
设平面的一个法向量,
取,得.
平面的一个法向量为,
,
,即二面角的正弦值为.
18.解:不妨设,
因为抛物线上一点到焦点的距离为,点到轴的距离为,
所以
整理得,解得或舍去,
则抛物线的方程为;
由题意知直线的斜率必存在,,
不妨设直线的方程为,,
联立,消去并整理得,,
由韦达定理得,
易知直线的方程为,
因为轴,所以,即,
所以,
因为,所以,
则直线的方程为,
因为,所以,
此时,
因为,
所以,
由题意知,则,
所以.
故的取值范围为.
19.解:,
,
,
,
所以关于的经验回归方程为.
记“恰有件产品为合格品”为事件,“类产品为合格品”为事件,
则,
,
由条件概率的计算公式得,
故在恰有件产品为合格品的条件下,类产品为合格品的概率为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,集合,则( )
A. B.
C. D.
2.设复数满足为虚数单位,则复数( )
A. B. C. D.
3.已知向量,,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4.重庆火锅、朝天门、解放碑、长江三峡、大足石刻、重庆人民大礼堂、合川钓鱼城、巫山人、铜梁龙舞、红岩村为重庆十大文化符号甲计划按照一定的先后顺序写一篇介绍重庆十大文化符号的文章,若第一个介绍的是重庆火锅,且长江三峡、大足石刻、重庆人民大礼堂、合川钓鱼城、巫山人的介绍顺序必须相邻这五大文化符号的介绍顺序中间没有其他文化符号,则该文章关于重庆十大文化符号的介绍顺序共有( )
A. 种 B. 种 C. 种 D. 种
5.如图为某年月份北京空气质量指数历史数据折线图,以下结论不正确的是( )
指数数值与等级水平表:
指数
等级 一级优 二级良 三级轻度污染 四级中度污染 五级重度污染 六级严重污染
A. 月份空气质量为优的天数为天
B. 月份连续天出现中度污染的概率为
C. 月份北京空气质量指数历史数据的众数为
D. 北京月至日这天的空气质量逐渐变好
6.如图,,,表示个开关,若在某段时间内它们正常工作的概率分别为,,,那么系统的可靠性为( )
A. B. C. D.
7.已知三棱锥的三条侧棱两两互相垂直,且,,,则此三棱锥的外接球的体积为( )
A. B. C. D.
8.已知,,,,则下列大小关系正确的是( )
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.年月日,某市物价部门对家商场的某商品一天的销售量及其价格进行调查,家商场的售价元和销售量件之间的一组数据如表所示:
售价
销售量
根据表中数据得到关于的回归直线方程是,则下列说法正确的有 .
A. B. 回归直线过点
C. 当时,的估计值为 D. 点处的随机误差为
10.下列结论正确的是( )
A. 若随机变量的方差,则
B. 若随机变量服从正态分布,且,则
C. 从装有大小、形状都相同的个红球和个白球的袋中随机取出两球,取到白球的个数记为,则
D. 若随机变量服从二项分布,则的分布列可表示为,
11.设抛物线的焦点为,是上的一个动点,则下列结论正确的是( )
A. 点到的距离比到轴的距离大
B. 点到直线的最小距离为
C. 以为直径的圆与轴相切
D. 记点在的准线上的射影为,则不可能是正三角形
三、填空题:本题共3小题,每小题5分,共15分。
12.数列中,,时,,则的通项公式是
13.若的展开式中的系数为,则展开式中所有项的二项式系数之和为 以数字作答
14.作家马伯庸小说长安十二时辰中,靖安司通过长安城内的望楼传递信息同名改编电视剧中,望楼传递信息的方式有一种如下:如图所示,在九宫格中,每个小方格可以在白色和紫色此处以阴影代表紫色之间变换,从而一共可以有种不同的颜色组合,即代表种不同的信息现要求每一行、每一列上都有且只有个紫色小方格如图所示即满足要求则一共可以传递 种信息用数字作答
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知数列的前项和为,.
求;
若,求数列的前项和.
16.本小题分
设函数.
若曲线在点处的切线方程是,求的值;
求函数的单调区间及极值.
17.本小题分
如图,在三棱柱中,是边长为的等边三角形,平面平面,,,为的中点,为的中点.
求证:平面;
求二面角的正弦值.
18.本小题分
已知抛物线上一点到焦点的距离为,点到轴的距离为.
求抛物线的方程;
过的直线交抛物线于,两点,过点作轴的垂线交直线是坐标原点于,过作直线的垂线与抛物线的另一交点为,直线与交于点求
19.本小题分
为进一步加强城市建设和产业集聚效应,某市通过“两化”中的信息化和工业化之间的完美交融结合,达到了经济效益的“倍增式”发展.该市某高科技企业对某核心技术加大研发投资力度,持续构建面向未来的竞争力.现得到一组在该技术研发投入单位:亿元与收益单位:亿元的数据如下表所示:
研发投入
收益
已知可用一元线性回归模型模型拟合与的关系,求此经验回归方程;附:对于一组数据,,,,其经验回归直线的斜率和截距的最小二乘法估计公式分别为,,,,结果保留两位小数
该企业主要生产、类产品,现随机抽取类产品件、类产品件进行质量检验,已知类、类产品独立检验为合格品的概率分别为,,求在恰有件产品为合格品的条件下,类产品为合格品的概率.
答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由题意,数列满足,
当时,可得,
两式相减,可得,整理得,即,
当时,可得,解得,
所以数列是首项为,公比为的等比数列,
所以,所以.
由知,则
设,数列的前项和分别为,
则
,
两式相减得,
所以,
又由,
所以数列的前项和.
16.解:曲线在点处的切线方程是,
,
所以,,
则,
解得.
因为,,
由,解得,
当时,,函数单调递增;
当时,,函数单调递减;
当时,,函数单调递增.
此时是的极大值点,是的极小值点,
的极大值为,
的极小值为.
函数单调递增区间为和;
函数单调递减区间为.
17.证明:取中点,连接,,
,, ,
三棱柱,为的中点,, ,
,四边形为平行四边形,
.
平面,平面,
平面
连接,,
,,,
平面平面,平面平面,
平面,平面,
,,
为等边三角形,
,,
两两垂直,
以为正交基底建立如图所示的空间直角坐标系,
,,,,.
,.
设平面的一个法向量为,
取,得.
平面的一个法向量为,
,.
设平面的一个法向量,
取,得.
平面的一个法向量为,
,
,即二面角的正弦值为.
18.解:不妨设,
因为抛物线上一点到焦点的距离为,点到轴的距离为,
所以
整理得,解得或舍去,
则抛物线的方程为;
由题意知直线的斜率必存在,,
不妨设直线的方程为,,
联立,消去并整理得,,
由韦达定理得,
易知直线的方程为,
因为轴,所以,即,
所以,
因为,所以,
则直线的方程为,
因为,所以,
此时,
因为,
所以,
由题意知,则,
所以.
故的取值范围为.
19.解:,
,
,
,
所以关于的经验回归方程为.
记“恰有件产品为合格品”为事件,“类产品为合格品”为事件,
则,
,
由条件概率的计算公式得,
故在恰有件产品为合格品的条件下,类产品为合格品的概率为.
第1页,共1页
同课章节目录
