湘教版数学八年级下册(新) 校本应用课件:2.2《平行四边形及其性质》(共23张PPT)
文档属性
| 名称 | 湘教版数学八年级下册(新) 校本应用课件:2.2《平行四边形及其性质》(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-19 20:34:55 | ||
图片预览





文档简介
课件23张PPT。2.2平行四边形的性质2.2.1 平行四边形的性质定义和性质例题和练习观察并动手小结及作业观察生活中的图形观察生活中的图形将一张纸对折,剪下两张叠放的三角形纸片。拿起剪下的两张三角形纸片,使它们相等的一组边重合,得到一个四边形。动一动手Return定义和表示方法
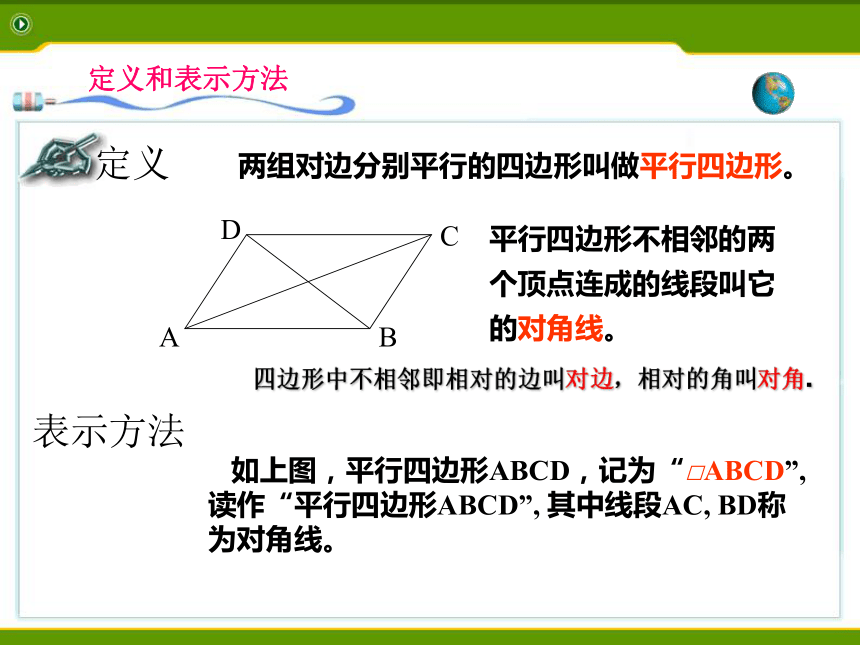
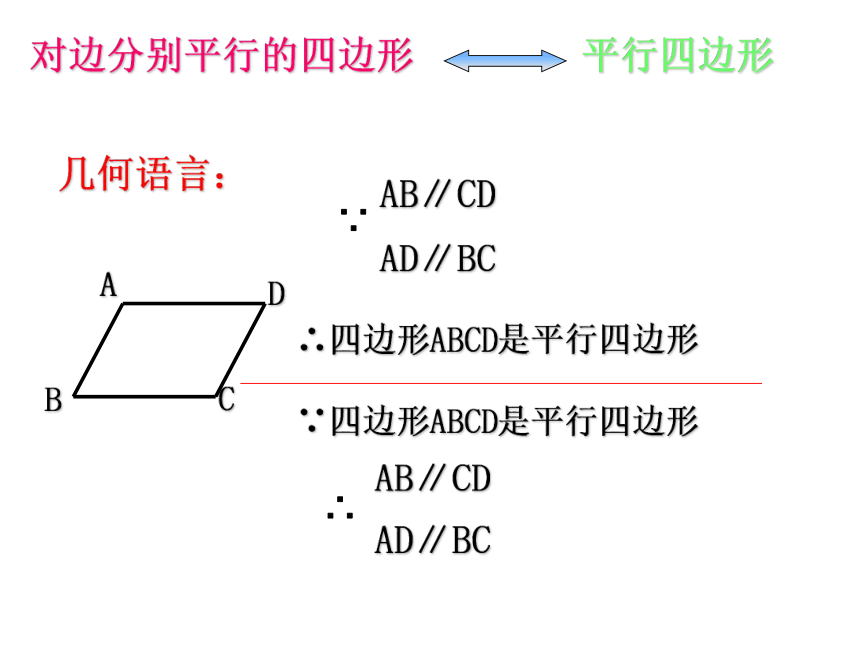
定义两组对边分别平行的四边形叫做平行四边形。 如上图,平行四边形ABCD,记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。表示方法平行四边形不相邻的两个顶点连成的线段叫它的对角线。四边形中不相邻即相对的边叫对边,相对的角叫对角.平行四边形对边分别平行的四边形几何语言:∵四边形ABCD是平行四边形∴四边形ABCD是平行四边形做一做将复制后的平行四边形绕一个顶点旋转180°,你能平移该纸片,使它与原来的四边形ABCD重合吗?对边之间、对角之间分别有什么关系?由此你能得到什么结论? 你能用别的方法验证这个结论吗?猜想平行四边形的性质平行四边形对边相等.平行四边形对角相等.证明:∵四边形ABCD是平行四边形∴AD∥BC ,AB∥CD(平行四边形定义)∴∠1=∠2, ∠3=∠4(两直线平行,内错角相等)∵BD=DB∴△ABD≌△CDB(ASA)∴∠A=∠C(全等三角形对应角相等)
AD=CB,AB=CD(全等三角形对应边相等)∵∠1=∠2, ∠3=∠4∴∠1+∠4=∠2+∠3(等式性质)即∠ABC=∠ADC∴ AD=CB,AB=CD,∠A=∠C,∠ABC=∠ADC4123DCBA证明猜想平行四边形对角相等.平行四边形对边相等.性质
用几何语言叙述性质平行四边形对边相等.平行四边形对边相等.∵四边形ABCD是平行四边形∴∵四边形ABCD是平行四边形∴Return例1.已知: 平行四边形ABCD,BD为对角线(如图) ∠A=70°, ∠BDC=30°, AD=15,
求: ∠C, ∠ADB的度数, 并求BC边的长. 解: ∵四边形ABCD 是平行四边形∴∠C=∠A=70°
∠ADC=180°-70°
= 110°又∵ ∠BDC=30°
∴ ∠ADB = 80°
而 BC = AD = 15
例2.如图,四边形ABCD是平行四边形,求:
(1)∠ADC,∠BCD的度数;
(2)边AB,BC的长度.解:(1)∵四边形ABCD是平行四边形∴∠B=∠ADC(平行四边形对角相等)
AB∥CD(平行四边形对边平行)∴∠B+∠BCD=180°
(两直线平行,同旁内角互补)∵∠B=56°∴∠ADC=∠B=56°∠BCD=180°-∠B=180°-56°=124°(2)∵四边形ABCD是平行四边形∴AD=BC,AB=CD(平行四边形对边相等)∵AD=30,CD=25 ∴BC=30,AB=25. 1. 在□ABCD中, ∠A=65°, 则∠B= °,
∠C= °, ∠D= °. 2. 在□ABCD中, AB+CD=28cm. □ABCD的周长
等于96cm, 则AB= , BC= , CD= ,
AD= . 1156511514cm34cm14cm34cm3.如下图中,EF∥BC, GH∥AB, EF与GH相交于点O,则图中共有___个平行四边形.9⒈平行四边形的两组对边分别平行。 ( )
⒉平行四边形的四个内角都相等。 ( )
⒊平行四边形的相邻两个内角的和等于180° ( )
⒋□ABCD中,如果∠A=30°,那么∠B=60° ( )√×√× 1. 已知平行四边形ABCD的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
解:∵在□ABCD中, 对边相等,
又∵□ABCD的周长为60cm.
∴AB + BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则 1.5BC + BC=30 , 解得 BC=12 (cm).
而 AB=1.5×12=18 (cm). 2.□ABCD中, ∠DAB:∠ABC=1:3 , ∠ACD= 25°,
求∠DAB, ∠DCB和∠ACB的度数 . 解:∵在□ABCD中, 相邻内角互补,
又∵ ∠DAB:∠ABC=1:3 ,
∴ ∠DAB= 45°, ∠ABC=135°.
又∵ □ABCD中,对角相等,
∴ ∠DCB =∠DAB=45°.
而∠ACB=∠DCB-∠ACD= 45°- 25°= 20°.Return课堂小结定 义表示方法性 质两组对边分别平行的四边形叫做 平 行 四边形。其不相邻的两个顶点连成的线段叫它的对角线。平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。1.平行四边形的两组对边分别平行;
2.平行四边形的对边相等,
3.平行四边形的对角相等, 相邻两角互补。今日作业:
教科书习题A组第1、2、3题.再见!
定义两组对边分别平行的四边形叫做平行四边形。 如上图,平行四边形ABCD,记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。表示方法平行四边形不相邻的两个顶点连成的线段叫它的对角线。四边形中不相邻即相对的边叫对边,相对的角叫对角.平行四边形对边分别平行的四边形几何语言:∵四边形ABCD是平行四边形∴四边形ABCD是平行四边形做一做将复制后的平行四边形绕一个顶点旋转180°,你能平移该纸片,使它与原来的四边形ABCD重合吗?对边之间、对角之间分别有什么关系?由此你能得到什么结论? 你能用别的方法验证这个结论吗?猜想平行四边形的性质平行四边形对边相等.平行四边形对角相等.证明:∵四边形ABCD是平行四边形∴AD∥BC ,AB∥CD(平行四边形定义)∴∠1=∠2, ∠3=∠4(两直线平行,内错角相等)∵BD=DB∴△ABD≌△CDB(ASA)∴∠A=∠C(全等三角形对应角相等)
AD=CB,AB=CD(全等三角形对应边相等)∵∠1=∠2, ∠3=∠4∴∠1+∠4=∠2+∠3(等式性质)即∠ABC=∠ADC∴ AD=CB,AB=CD,∠A=∠C,∠ABC=∠ADC4123DCBA证明猜想平行四边形对角相等.平行四边形对边相等.性质
用几何语言叙述性质平行四边形对边相等.平行四边形对边相等.∵四边形ABCD是平行四边形∴∵四边形ABCD是平行四边形∴Return例1.已知: 平行四边形ABCD,BD为对角线(如图) ∠A=70°, ∠BDC=30°, AD=15,
求: ∠C, ∠ADB的度数, 并求BC边的长. 解: ∵四边形ABCD 是平行四边形∴∠C=∠A=70°
∠ADC=180°-70°
= 110°又∵ ∠BDC=30°
∴ ∠ADB = 80°
而 BC = AD = 15
例2.如图,四边形ABCD是平行四边形,求:
(1)∠ADC,∠BCD的度数;
(2)边AB,BC的长度.解:(1)∵四边形ABCD是平行四边形∴∠B=∠ADC(平行四边形对角相等)
AB∥CD(平行四边形对边平行)∴∠B+∠BCD=180°
(两直线平行,同旁内角互补)∵∠B=56°∴∠ADC=∠B=56°∠BCD=180°-∠B=180°-56°=124°(2)∵四边形ABCD是平行四边形∴AD=BC,AB=CD(平行四边形对边相等)∵AD=30,CD=25 ∴BC=30,AB=25. 1. 在□ABCD中, ∠A=65°, 则∠B= °,
∠C= °, ∠D= °. 2. 在□ABCD中, AB+CD=28cm. □ABCD的周长
等于96cm, 则AB= , BC= , CD= ,
AD= . 1156511514cm34cm14cm34cm3.如下图中,EF∥BC, GH∥AB, EF与GH相交于点O,则图中共有___个平行四边形.9⒈平行四边形的两组对边分别平行。 ( )
⒉平行四边形的四个内角都相等。 ( )
⒊平行四边形的相邻两个内角的和等于180° ( )
⒋□ABCD中,如果∠A=30°,那么∠B=60° ( )√×√× 1. 已知平行四边形ABCD的周长为60cm,两邻边AB,BC长的比为3:2,求AB和BC的长度 .
解:∵在□ABCD中, 对边相等,
又∵□ABCD的周长为60cm.
∴AB + BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则 1.5BC + BC=30 , 解得 BC=12 (cm).
而 AB=1.5×12=18 (cm). 2.□ABCD中, ∠DAB:∠ABC=1:3 , ∠ACD= 25°,
求∠DAB, ∠DCB和∠ACB的度数 . 解:∵在□ABCD中, 相邻内角互补,
又∵ ∠DAB:∠ABC=1:3 ,
∴ ∠DAB= 45°, ∠ABC=135°.
又∵ □ABCD中,对角相等,
∴ ∠DCB =∠DAB=45°.
而∠ACB=∠DCB-∠ACD= 45°- 25°= 20°.Return课堂小结定 义表示方法性 质两组对边分别平行的四边形叫做 平 行 四边形。其不相邻的两个顶点连成的线段叫它的对角线。平行四边形ABCD, 记为“□ABCD”, 读作“平行四边形ABCD”, 其中线段AC, BD称为对角线。1.平行四边形的两组对边分别平行;
2.平行四边形的对边相等,
3.平行四边形的对角相等, 相邻两角互补。今日作业:
教科书习题A组第1、2、3题.再见!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
