沪科版八年级数学上册试题 期中综合复习卷(含解析)
文档属性
| 名称 | 沪科版八年级数学上册试题 期中综合复习卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 12:51:28 | ||
图片预览




文档简介
期中综合复习卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列命题是假命题的是( )
A.若,则 B.若,则
C.若,则 D.若两个角的和为90°,则这两个角互余
2.点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是( )
A.(4,﹣3) B.(4,3) C.(3,﹣4) D.(﹣3,4)
3.已知两点A(﹣1,3),B(2,﹣3),现将线段AB平移至,如果(a,1),B1(5,﹣b),那么的值是( )
A.16 B.25 C.32 D.49
4.如图,点A,B,C在一次函数的图象上,它们的横坐标依次为,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A.1 B.3 C. D.
5.有六根细木棒,它们的长度分别是1,2,3,4,5,6(单位:).若从中取出三根,首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为( )
A.1,2,3 B.2,3,4 C.3.4,5 D.4,5,6
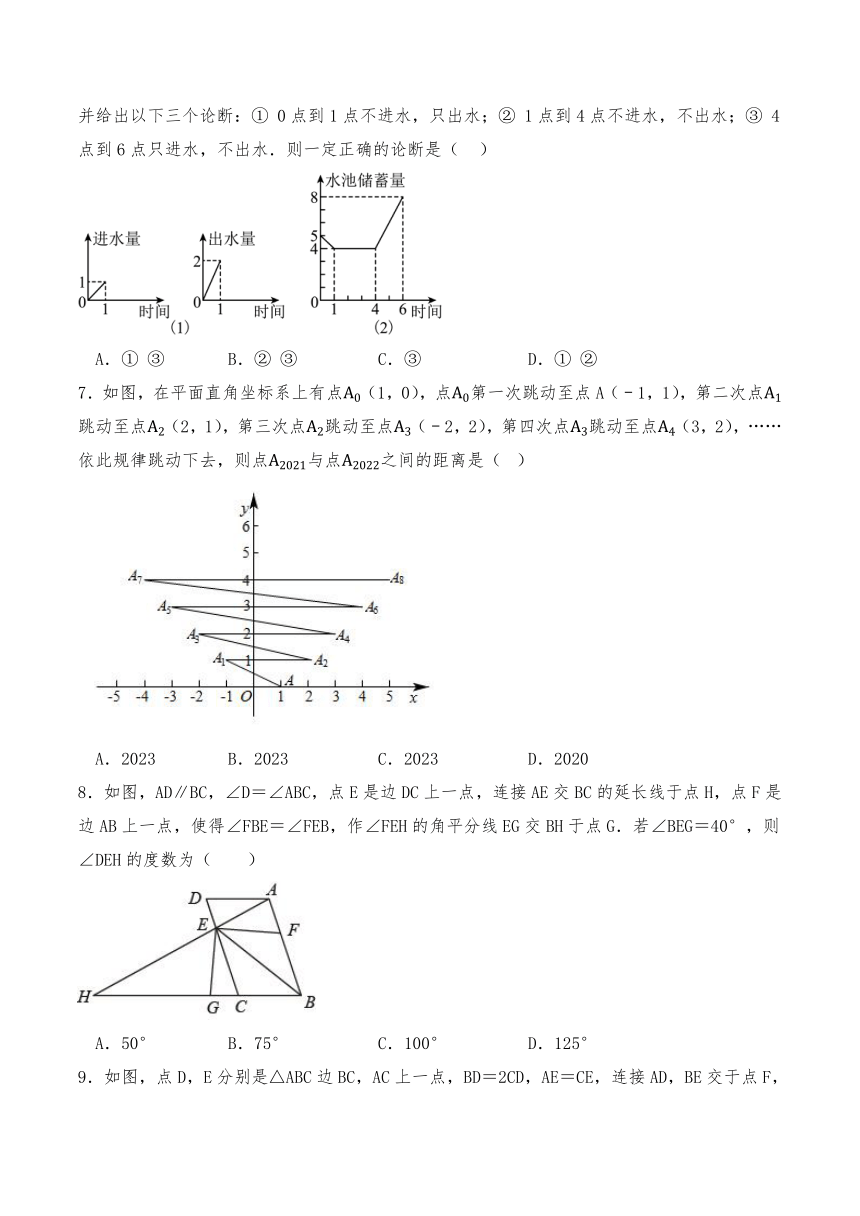
6.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同),一个进水管和一个出水管的进出水速度如图(1)所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图(2)所示,并给出以下三个论断:① 0点到1点不进水,只出水;② 1点到4点不进水,不出水;③ 4点到6点只进水,不出水.则一定正确的论断是( )
A.① ③ B.② ③ C.③ D.① ②
7.如图,在平面直角坐标系上有点(1,0),点第一次跳动至点A(﹣1,1),第二次点跳动至点(2,1),第三次点跳动至点(﹣2,2),第四次点跳动至点(3,2),……依此规律跳动下去,则点与点之间的距离是( )
A.2023 B.2023 C.2023 D.2020
8.如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G.若∠BEG=40°,则∠DEH的度数为( )
A.50° B.75° C.100° D.125°
9.如图,点D,E分别是△ABC边BC,AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为18,则△BDF与△AEF的面积之差S△BDF﹣S△AEF等于( )
A.3 B. C. D.6
10.甲、乙两人沿同一条笔直的公路相向而行,甲从地前往地,乙从地前往地.甲先出发3分钟后乙才出发.当甲行驶到6分钟时发现重要物品忘带,立刻以原速的掉头返回地.拿到物品后以提速后的速度继续前往地,二人相距的路程(米)与甲出发的时间(分钟)之间的关系如图所示,下列说法不正确的是( )
A.乙的速度为 B.两人第一次相遇的时间是分钟
C.点的坐标为 D.甲最终达到地的时间是分钟
二.填空题(共6小题,满分18分,每小题3分)
11.平面直角坐标系内轴,,点的坐标为,则点的坐标为______ .
12.在下列条件中:①;②;③,能确定为直角三角形的条件有_________个.
13.一次函数的图象与两坐标轴围成的三角形的面积等于5,则该直线的表达式为________.
14.如图,在平面直角坐标系中,直线,直线与正半轴交于点,与负半轴交于点,直线与正半轴交于点,若直线的函数表达式为,,,则的值为______.
15.在平面直角坐标系中,垂直x轴的直线l分别与函数的图像交于P、Q两点,若平移直线l,可以使P、Q都在x轴的下方,则实数a的取值范围是_________.
16.如图,在四边形ABCD中,的角平分线与的外角平分线相交于点P,且,则______.
三.解答题(共9小题,满分72分)
17.(6分)如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到.
(1)在图中画出;
(2)写出,的坐标;
(3)求的面积.
18.(6分)已知点请分别根据下列条件,求出点P的坐标,
(1)点P在第一,三象限的角平分线上;
(2)点P的纵坐标比横坐标大5;
(3)点P在过点且与y轴平行的直线上.
19.(6分)已知,在中.
(1)若,,求的各内角度数;
(2)若三边长分别为a、b、c,试化简代数式.
20.(8分)如图,直线:y=2x-2与x轴交于点D,直线:y=kx+b与x轴交于点A,且经过点,直线,交于点.
(1)求m的值;
(2)求直线的解析式;
(3)根据图象,直接写出1<kx+b<2x-2的解集
21.(8分)如图,在平面直角坐标系中,直线过点且与轴交于点,点关于轴的对称点为点,过点且与直线平行的直线交轴于点,连接.
(1)求的值及直线的解析式;
(2)在轴上是否存在点,使的面积是面积的?如果存在,求出点的坐标;如果不存在,请说明理由.
22.(9分)某区市政园林局为了绿化北井大道,要在思源实验学校至碧桂园天玺台小区之间的道路两旁,新栽一批成形大树,准备栽种黄葛树和梧桐树.若购买5棵黄葛树和3棵梧桐树,需要6600元;若购买2棵黄葛树和3棵梧桐树,需要3900元.
(1)求黄葛树和梧桐树每棵各是多少元?
(2)市政园林局计划购买黄葛树和梧桐树共84棵,且购买梧桐树的数量不超过黄葛树数量的一半.设购买梧桐树x棵,购买两种树苗所需要的费用为y元.
①求y与x之间的函数关系式;
②哪种采购方案费用最少?并求出最少的采购费用.
23.(9分)如图1,A、B两地之间有一C地,货车和客车分别从A、B两地同时出发,匀速行驶,相向而行,货车到达C地后继续行驶到B地,客车到达C地后停止,客车和货车到C地的距离分别为、(千米),与行驶时间x(小时)之间的函数关系如图2所示.
(1)A、B两地之间的距离是___________千米.
(2)求两小时后,货车到C地的距离与行驶时间x(小时)之间的函数关系.
(3)直接写出两车出发多长时间,它们与C地的距离相等.
24.(10分)如图①.已知,点B为平面内一点,于点B,过点B作于点D,设.
(1)若,求的度数;
(2)如图②,若点E、F在DM上,连接BE、BF、CF,使得BE平分∠ABD、BF平分∠DBC,求的度数;
(3)如图③,在(2)问的条件下,若CF平分,且,求的度数.
25.(10分)如图①,四边形ABCD中,,.
(1)动点M从A出发,以每秒1个单位的速度沿路线A→B→C→D运动到D停止.设运动时间为t,△AMD的面积为S,S关于t的函数图象如图②所示,则AD= ,CD= ;
(2)在(1)的条件下,当点M在线段BC上运动时,请写出S与t的关系式;
(3)在(1)的条件下,当S=52时,t等于多少?
(4)如图③,动点P从点A出发,以每秒2个单位的速度沿路线A→D→C运动到点C停止,同时,动点Q从点C出发,以每秒5个单位的速度沿路线C→D→A运动到点A停止.设运动时间为t,当Q点运动到AD边上时,连接CP、CQ、PQ,当△CPQ的面积为8时,直接写出t的值.
答案解析
一.选择题
1.B
【分析】根据等式的性质判断A正确;根据不等式的性质判断B错误;根据绝对值的定义及性质判断C正确;根据角互余的定义判断D正确.
【详解】解:A、根据等式的性质:等式两边加上同一个数等式依然成立可知若,则,该选项不符合题意;
B、根据不等式的性质:不等式两边同乘一个负数不等号方向改变可知若,则,该选项符合题意;
C、根据绝对值的定义与性质可知若,则,该选项不符合题意;
D、根据角互余的定义可知若两个角的和为90°,则这两个角互余,该选项不符合题意;
故选:B.
2.A
【分析】根据第四象限内点的符号特征:横坐标为正,纵坐标为负;以及点到坐标轴的距离的意义,即可进行解答.
【详解】解:令点M的坐标为(a,b)
∵点M到x轴的距离为3,到y轴的距离为4,
∴,
∵点M在第四象限,
∴a=4,b=﹣3,
∴M(4,﹣3),
故选:A.
3.C
【分析】根据平移的性质,结合已知点A,B的坐标,根据平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减,可得出a,b的值,即可得到答案.
【详解】解:∵A(-1,3)平移后对应点的坐标为(a,1),
∴线段向下平移了2个单位,
∵点B(2,-3)平移后对应的点(5,-b),
∴线段向右平移了3个单位,
∴a=2,b=5,
∴,
故选:C.
4.B
【分析】设AD⊥y轴于点D;BF⊥y轴于点F;BG⊥CG于点G,然后求出A、B、C、D、E、F、G各点的坐标,计算出长度,利用三角形面积公式即可计算出答案.
【详解】解:如图,
由题意可得:A点坐标为(-1,2+m),B点坐标为(1,-2+m),
C点坐标为(2,m-4),D点坐标为(0,2+m),
E点坐标为(0,m),F点坐标为(0,-2+m),G点坐标为(1,m-4).
所以,DE=EF=BG=2+m-m=m-(-2+m)=-2+m-(m-4)=2,
又因为AD=BF=GC=1,
所以图中阴影部分的面积和等于.
故选:B.
5.C
【分析】根据较小的两根木棒长的平方和是否等于最大的一根木棒长的平方,逐一判定.
【详解】A. 1,2,3;
∵1+2=3,
∴这三根木棒不能搭成一个直角三角形;
B. 2,3,4;
∵,,
∴,
∴这三根木棒不能搭成一个直角三角形;
C. 3.4,5;
∵,,
∴,
∵3+4>5,
∴这三根木棒能搭成一个直角三角形;
D. 4,5,6;
∵,,
∴,
∴这三根木棒不能搭成一个直角三角形.
故选C.
6.C
【分析】根据图像(1)可知进水速度小于出水速度,结合图(2)中特殊点的实际意义即可作出判断
【详解】解:由图(1)知:一个管子单位时间进水量为1,出水量为2
① 结合图(2)知:
0点到1点,储蓄量减少1,
即2-1×1=1
所以开了一个出水管,开了一个进水管,
所以0点到1点既进水,也出水
故① 的说法错误
② 由图(2)知:
水池的储水量1点到4点没有发生变化
即:3×(2-1×2)=0
所以开了一个出水管,两个进水管
故② 的说法错误
③ 由图(2)知:4点6点水池蓄水量增加了4
即1×2×2=4
所以打开了2个进水管,没有打开出水管
所以4点到6点只进水,不出水
故③ 对
故选:C
7.A
【分析】根据图形观察发现,第偶数次跳动至点的坐标,横坐标是次数的一半加上1,纵坐标是次数的一半,奇数次跳动与该偶数次跳动的横坐标的相反数加上1,纵坐标相同,可分别求出点与点的坐标,进而可求出点与点之间的距离.
【详解】解:观察发现,第2次跳动至点的坐标是(2,1),
第4次跳动至点的坐标是(3,2),
第6次跳动至点的坐标是(4,3),
第8次跳动至点的坐标是(5,4),
…
第2n次跳动至点的坐标是(n+1,n),
则第2023次跳动至点的坐标是(1012,1011),
第2023次跳动至点的坐标是(-1011,1011).
∵点与点的纵坐标相等,
∴点与点之间的距离=1012-(-1011)=2023,
故选:A.
8.C
【分析】∠BEG=∠FEG-∠FEB=,∠AEF=180°-∠FEG-∠HEG=180°-2β,在△AEF中,,AD∥BC,∠D=∠ABC,得到AB∥CD,由平行线的性质和邻补角的定义即可求解.
【详解】解:设∠FBE=∠FEB=α,则∠AFE=2α,
∠FEH的角平分线为EG,设∠GEH=∠GEF=β,
∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠D=∠ABC,
∴∠D+∠BAD=180°,
∴AB∥CD,
∵∠BEG=40°,
∴∠BEG=∠FEG-∠FEB=β-α=40°,
∵∠AEF=180°-∠FEG-∠HEG=180°-2β,
在△AEF中,180°-2β+2α+∠FAE=180°,
∴∠FAE=2β-2α=2(β-α)=80°,
∵AB∥CD,
∴∠CEH=∠FAE=80°,
∴∠DEH=180°-∠CEH=100°.
故选:C.
9.A
【分析】由△ABC的面积为18,根据三角形的面积公式和等积代换即可求得.
【详解】解:∵,
∴,
∵,,,
∴,
∴①,
同理,∵,,
∴,,
∴,
∴②,
由①-②得:.
故选:A.
10.D
【分析】甲出发3分钟后乙才出发,则AB段表示甲先出发3分钟内两人距离与甲出发时间的关系,故可得B点横坐标为3;BC段表示甲3分钟~6分钟内两人的距离与甲出发时间的关系,故可得点C横坐标为6;CD段两人距离不变,表示两人的速度相等,从而可得乙的速度为甲原来速度的,利用前6分钟的路程等于返回取物品的路程,可求得D点的横坐标,再利用相遇关系可求得第一次相遇的时间,从而也可求得甲最终达到B地的时间,从而确定答案.
【详解】由题意知:AB段表示甲先出发3分钟内两人距离与甲出发时间的关系,则;BC段表示甲3分钟~6分钟内两人的距离与甲出发时间的关系,故;CD段两人距离不变,表示两人的速度相等,从而可得乙的速度为甲原来速度的;设甲原来的速度为,提速后的速度为,则乙的速度为
甲行驶6分钟后,乙行驶3分钟,两人相距2320米,于是两人共行驶了4000 2320=1680()
则得方程:
解得:
则乙的速度为
故A正确
甲前3分钟的路程为:3×160=480(),3分钟时甲乙相距
故点B的坐标为
故C正确
设甲6分钟后返回的时间为
根据甲6分钟的路程=甲返回取回物品的路程,得方程:
解得:t=4
∴
即10后,甲乙均以速度相向而行,此时两人相距:,两人相遇的时间为:
所以甲出发到两人第一次相遇时间为:
故B正确
甲拿回物品后到达B地需要的时间为:,则甲最终达到B地所需的时间为:
故D错误
故选:D
二.填空题
11.(-3,-3)或(7,-3)##(7,-3)或(-3,-3)
【分析】根据平行于轴的直线是上的点的纵坐标相等求出点的纵坐标,再分点在点的左边与右边两种情况求出点的横坐标,即可得解.
【详解】解:∵轴轴,点的坐标为,
点的横坐标为,
,
点在点的左边时,横坐标为,
点在点的右边时,横坐标为,
点的坐标为或.
故答案为:或.
12.3
【分析】利用三角形的内角和定理,即可分别进行判断.
【详解】解:①∵,
又∵,
∴,
∴;故①符合题意;
②∵,
又;
∴,
∴;故②符合题意;
③∵,
又,
∴,
故③符合题意;
∴能确定为直角三角形的条件有3个;
故答案为:3.
13.或
【分析】先求出直线与坐标轴的交点坐标,再根据三角形的面积公式得到,求出k即可.
【详解】解:
当x=0时,y=10
∴与y轴交于点(0,10)
当y=0时,,
∴与x轴交于点,
∵围成的三角形的面积为5,
∴,
解得
∴该直线的表达式为或
故答案为:或.
14.1
【分析】根据题意求出的坐标,再根据,列出方程即可得出答案.
【详解】解:∵直线,直线的函数表达式为:,
∴设直线的函数表达式为:,
当时,,
∴,
∴,
∵,
∴,
∴,
把代入得:,
∴,
∴,
当时,,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵直线与正半轴交于点,
∴,
∴,
故答案为:.
15.
【分析】根据题意可知在时,有公共解,因此可以列出不等式,从而得到答案.
【详解】令,则,
令,则,
∵平移直线,可以使P、Q都在轴的下方,
∴可知在时,有公共解,
∴,解得:,
故填:.
16.
【分析】先根据角平分线的定义可得,,再根据四边形的内角和可得,然后根据三角形的外角性质即可得.
【详解】解:∵的角平分线与的外角平分线相交于点P,
∴,,
∵在四边形ABCD中,,
∴,
由三角形的外角性质得:,
.
故答案为:.
三.解答题
17.
(1)
如图所示:△A′B′C′即为所求;
(2)
由图可知,点,的坐标分别是:(0,4)(-1,1);
(3)
由图可知:,()
的面积为:.
18.
(1)
∵点P在一、三象限角平分线上,
∴.
∴,
∴,
∴点P的坐标;
(2)
∵点P的纵坐标比横坐标大5,
∴.
解得.
∴.
∴点P的坐标;
(3)
由题意知轴,
∴点A和点P的横坐标相同.
即,
解得.
∴.
∴点P的坐标为.
19.(1)解:,,
又,
,
,
,
.
,.
(2)解:∵三边长分别为a、b、c,
∴,,
∴|a+b﹣c|﹣|b﹣c﹣a|,
=a+b﹣c﹣(﹣b+c+a),
=a+b﹣c+b﹣a﹣c,
=2b﹣2c.
20.
(1)
把代入y=2x-2,
得2m-2=2,
解得m=2,
即m的值是2;
(2)
把,代入y=kx+b,
得,
解得,
∴直线的解析式为;
(3)
由图象可得,1<kx+b<2x-2的解集是2<x<3.
21.
(1)
解:直线过点,
,
,
点关于轴的对称点为点.
,
直线与直线平行,
设直线的解析式为,
代入得,,
解得,
直线的解析式为;
(2)
解:在直线中,令,则,
,
在直线中,令,则,
,
,,
,
设,
的面积是面积的,
,
,
,
或.
22.
(1)
解:设黄葛树的单价每棵a元,梧桐树的单价每棵b元,
由题意,得
,
解得:.
答:黄葛树的单价是每棵900元,梧桐树的单价是每棵700元.
(2)
解:①由题意,得
y=700x+900(84-x)
化简得y=-200x+75600
∴y与x之间的函数关系式为:y=-200x+75600;
②∵k=-200<0,
∴y随x的增大而减小.
∵x≤,
∴x≤28,
∴x=28时, =70000,
∴采购方案是:梧桐树采购28棵,黄葛树采购56棵,最少费用是70000元.
23.
(1)
解:根据题意得,AC=90km,BC=540km,
∴ km
故答案为:630;
(2)
解:∵货车从A地到C地行驶90km,用时2h,
∴货车的平均速度为: km/h,
∴行驶540km所用时间为:540÷45=12(h),
∴货车从A地出发到达B地所用时间为14h,
设货车从C到B的函数关系式为,
把(2,0)和(14,540)代入,得,
解得,
∴货车从C到B的函数关系式为;
(3)
解:设,
把(0,540)和(9,0)代入,得,
解得,
∴,
由题意可知:和的交点即为到C点距离相等,
联立方程组,
解得,
∴两车出发6小时,它们与C地的距离相等.
24.(1)
解:延长DB,交NC于点H,如图,
∵,,
∴,
∴.
∵,
∴.
∵,
∴.
∴;
(2)
解:延长DB,交NC于点H,如图,
∵,,
∴.∴.
∵,∴.
∵,∴,
∴.
∵BE平分,
∴.
∵,
∴.
∵BF平分,
∴.
∴;
(3)
解:∵,
∴.
∵CF平分,
∴.
∵,
∴.
∵,
∴.
∴.
由(2)知:.
∵,∴.
∴,
∴,
解得:.
∴,
∴.
25.
(1)
解:由函数图象可知,点M从A出发,从点C到D耗时秒,
,
此时,解得,
故答案为:12,16.
(2)
解:当点M在线段BC上运动时,,
设一次函数的解析式为,
将点代入得:,
解得,
∴.
(3)
解:当点M在BC上,即时,则,
解得,
当点M在CD上,即时,则,
解得,
∴,
∴在(1)的条件下,当时,等于10或.
(4)
解:由题意得,当Q运动到A停止的时间为,而点P运动到D的时间为,
(1)当点P、Q都在AD边上,此时有以PQ为底边,CD为高的三角形CPQ,
设运动的时间为t,则AP=2t,DQ=5t﹣16,
由得:,
,
①当点P在上方时,则PQ=AD﹣AP﹣QD=12﹣2t﹣5t+16=28﹣7t,
则△CPQ的面积为,解得,符合题意;
②当点P在点Q下方时,,
则△CPQ的面积为,解得,符合题意;
(2)当点P在CD上时,点Q运动到A时,则,
则△CPQ的面积为,解得,符合题意;
综上,的值为或或.
一.选择题(共10小题,满分30分,每小题3分)
1.下列命题是假命题的是( )
A.若,则 B.若,则
C.若,则 D.若两个角的和为90°,则这两个角互余
2.点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是( )
A.(4,﹣3) B.(4,3) C.(3,﹣4) D.(﹣3,4)
3.已知两点A(﹣1,3),B(2,﹣3),现将线段AB平移至,如果(a,1),B1(5,﹣b),那么的值是( )
A.16 B.25 C.32 D.49
4.如图,点A,B,C在一次函数的图象上,它们的横坐标依次为,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积之和是( )
A.1 B.3 C. D.
5.有六根细木棒,它们的长度分别是1,2,3,4,5,6(单位:).若从中取出三根,首尾顺次连接搭成一个直角三角形,则这三根木棒的长度分别为( )
A.1,2,3 B.2,3,4 C.3.4,5 D.4,5,6
6.为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同),一个进水管和一个出水管的进出水速度如图(1)所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图(2)所示,并给出以下三个论断:① 0点到1点不进水,只出水;② 1点到4点不进水,不出水;③ 4点到6点只进水,不出水.则一定正确的论断是( )
A.① ③ B.② ③ C.③ D.① ②
7.如图,在平面直角坐标系上有点(1,0),点第一次跳动至点A(﹣1,1),第二次点跳动至点(2,1),第三次点跳动至点(﹣2,2),第四次点跳动至点(3,2),……依此规律跳动下去,则点与点之间的距离是( )
A.2023 B.2023 C.2023 D.2020
8.如图,AD∥BC,∠D=∠ABC,点E是边DC上一点,连接AE交BC的延长线于点H,点F是边AB上一点,使得∠FBE=∠FEB,作∠FEH的角平分线EG交BH于点G.若∠BEG=40°,则∠DEH的度数为( )
A.50° B.75° C.100° D.125°
9.如图,点D,E分别是△ABC边BC,AC上一点,BD=2CD,AE=CE,连接AD,BE交于点F,若△ABC的面积为18,则△BDF与△AEF的面积之差S△BDF﹣S△AEF等于( )
A.3 B. C. D.6
10.甲、乙两人沿同一条笔直的公路相向而行,甲从地前往地,乙从地前往地.甲先出发3分钟后乙才出发.当甲行驶到6分钟时发现重要物品忘带,立刻以原速的掉头返回地.拿到物品后以提速后的速度继续前往地,二人相距的路程(米)与甲出发的时间(分钟)之间的关系如图所示,下列说法不正确的是( )
A.乙的速度为 B.两人第一次相遇的时间是分钟
C.点的坐标为 D.甲最终达到地的时间是分钟
二.填空题(共6小题,满分18分,每小题3分)
11.平面直角坐标系内轴,,点的坐标为,则点的坐标为______ .
12.在下列条件中:①;②;③,能确定为直角三角形的条件有_________个.
13.一次函数的图象与两坐标轴围成的三角形的面积等于5,则该直线的表达式为________.
14.如图,在平面直角坐标系中,直线,直线与正半轴交于点,与负半轴交于点,直线与正半轴交于点,若直线的函数表达式为,,,则的值为______.
15.在平面直角坐标系中,垂直x轴的直线l分别与函数的图像交于P、Q两点,若平移直线l,可以使P、Q都在x轴的下方,则实数a的取值范围是_________.
16.如图,在四边形ABCD中,的角平分线与的外角平分线相交于点P,且,则______.
三.解答题(共9小题,满分72分)
17.(6分)如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到.
(1)在图中画出;
(2)写出,的坐标;
(3)求的面积.
18.(6分)已知点请分别根据下列条件,求出点P的坐标,
(1)点P在第一,三象限的角平分线上;
(2)点P的纵坐标比横坐标大5;
(3)点P在过点且与y轴平行的直线上.
19.(6分)已知,在中.
(1)若,,求的各内角度数;
(2)若三边长分别为a、b、c,试化简代数式.
20.(8分)如图,直线:y=2x-2与x轴交于点D,直线:y=kx+b与x轴交于点A,且经过点,直线,交于点.
(1)求m的值;
(2)求直线的解析式;
(3)根据图象,直接写出1<kx+b<2x-2的解集
21.(8分)如图,在平面直角坐标系中,直线过点且与轴交于点,点关于轴的对称点为点,过点且与直线平行的直线交轴于点,连接.
(1)求的值及直线的解析式;
(2)在轴上是否存在点,使的面积是面积的?如果存在,求出点的坐标;如果不存在,请说明理由.
22.(9分)某区市政园林局为了绿化北井大道,要在思源实验学校至碧桂园天玺台小区之间的道路两旁,新栽一批成形大树,准备栽种黄葛树和梧桐树.若购买5棵黄葛树和3棵梧桐树,需要6600元;若购买2棵黄葛树和3棵梧桐树,需要3900元.
(1)求黄葛树和梧桐树每棵各是多少元?
(2)市政园林局计划购买黄葛树和梧桐树共84棵,且购买梧桐树的数量不超过黄葛树数量的一半.设购买梧桐树x棵,购买两种树苗所需要的费用为y元.
①求y与x之间的函数关系式;
②哪种采购方案费用最少?并求出最少的采购费用.
23.(9分)如图1,A、B两地之间有一C地,货车和客车分别从A、B两地同时出发,匀速行驶,相向而行,货车到达C地后继续行驶到B地,客车到达C地后停止,客车和货车到C地的距离分别为、(千米),与行驶时间x(小时)之间的函数关系如图2所示.
(1)A、B两地之间的距离是___________千米.
(2)求两小时后,货车到C地的距离与行驶时间x(小时)之间的函数关系.
(3)直接写出两车出发多长时间,它们与C地的距离相等.
24.(10分)如图①.已知,点B为平面内一点,于点B,过点B作于点D,设.
(1)若,求的度数;
(2)如图②,若点E、F在DM上,连接BE、BF、CF,使得BE平分∠ABD、BF平分∠DBC,求的度数;
(3)如图③,在(2)问的条件下,若CF平分,且,求的度数.
25.(10分)如图①,四边形ABCD中,,.
(1)动点M从A出发,以每秒1个单位的速度沿路线A→B→C→D运动到D停止.设运动时间为t,△AMD的面积为S,S关于t的函数图象如图②所示,则AD= ,CD= ;
(2)在(1)的条件下,当点M在线段BC上运动时,请写出S与t的关系式;
(3)在(1)的条件下,当S=52时,t等于多少?
(4)如图③,动点P从点A出发,以每秒2个单位的速度沿路线A→D→C运动到点C停止,同时,动点Q从点C出发,以每秒5个单位的速度沿路线C→D→A运动到点A停止.设运动时间为t,当Q点运动到AD边上时,连接CP、CQ、PQ,当△CPQ的面积为8时,直接写出t的值.
答案解析
一.选择题
1.B
【分析】根据等式的性质判断A正确;根据不等式的性质判断B错误;根据绝对值的定义及性质判断C正确;根据角互余的定义判断D正确.
【详解】解:A、根据等式的性质:等式两边加上同一个数等式依然成立可知若,则,该选项不符合题意;
B、根据不等式的性质:不等式两边同乘一个负数不等号方向改变可知若,则,该选项符合题意;
C、根据绝对值的定义与性质可知若,则,该选项不符合题意;
D、根据角互余的定义可知若两个角的和为90°,则这两个角互余,该选项不符合题意;
故选:B.
2.A
【分析】根据第四象限内点的符号特征:横坐标为正,纵坐标为负;以及点到坐标轴的距离的意义,即可进行解答.
【详解】解:令点M的坐标为(a,b)
∵点M到x轴的距离为3,到y轴的距离为4,
∴,
∵点M在第四象限,
∴a=4,b=﹣3,
∴M(4,﹣3),
故选:A.
3.C
【分析】根据平移的性质,结合已知点A,B的坐标,根据平移规律,左右移,纵不变,横减加,上下移,横不变,纵加减,可得出a,b的值,即可得到答案.
【详解】解:∵A(-1,3)平移后对应点的坐标为(a,1),
∴线段向下平移了2个单位,
∵点B(2,-3)平移后对应的点(5,-b),
∴线段向右平移了3个单位,
∴a=2,b=5,
∴,
故选:C.
4.B
【分析】设AD⊥y轴于点D;BF⊥y轴于点F;BG⊥CG于点G,然后求出A、B、C、D、E、F、G各点的坐标,计算出长度,利用三角形面积公式即可计算出答案.
【详解】解:如图,
由题意可得:A点坐标为(-1,2+m),B点坐标为(1,-2+m),
C点坐标为(2,m-4),D点坐标为(0,2+m),
E点坐标为(0,m),F点坐标为(0,-2+m),G点坐标为(1,m-4).
所以,DE=EF=BG=2+m-m=m-(-2+m)=-2+m-(m-4)=2,
又因为AD=BF=GC=1,
所以图中阴影部分的面积和等于.
故选:B.
5.C
【分析】根据较小的两根木棒长的平方和是否等于最大的一根木棒长的平方,逐一判定.
【详解】A. 1,2,3;
∵1+2=3,
∴这三根木棒不能搭成一个直角三角形;
B. 2,3,4;
∵,,
∴,
∴这三根木棒不能搭成一个直角三角形;
C. 3.4,5;
∵,,
∴,
∵3+4>5,
∴这三根木棒能搭成一个直角三角形;
D. 4,5,6;
∵,,
∴,
∴这三根木棒不能搭成一个直角三角形.
故选C.
6.C
【分析】根据图像(1)可知进水速度小于出水速度,结合图(2)中特殊点的实际意义即可作出判断
【详解】解:由图(1)知:一个管子单位时间进水量为1,出水量为2
① 结合图(2)知:
0点到1点,储蓄量减少1,
即2-1×1=1
所以开了一个出水管,开了一个进水管,
所以0点到1点既进水,也出水
故① 的说法错误
② 由图(2)知:
水池的储水量1点到4点没有发生变化
即:3×(2-1×2)=0
所以开了一个出水管,两个进水管
故② 的说法错误
③ 由图(2)知:4点6点水池蓄水量增加了4
即1×2×2=4
所以打开了2个进水管,没有打开出水管
所以4点到6点只进水,不出水
故③ 对
故选:C
7.A
【分析】根据图形观察发现,第偶数次跳动至点的坐标,横坐标是次数的一半加上1,纵坐标是次数的一半,奇数次跳动与该偶数次跳动的横坐标的相反数加上1,纵坐标相同,可分别求出点与点的坐标,进而可求出点与点之间的距离.
【详解】解:观察发现,第2次跳动至点的坐标是(2,1),
第4次跳动至点的坐标是(3,2),
第6次跳动至点的坐标是(4,3),
第8次跳动至点的坐标是(5,4),
…
第2n次跳动至点的坐标是(n+1,n),
则第2023次跳动至点的坐标是(1012,1011),
第2023次跳动至点的坐标是(-1011,1011).
∵点与点的纵坐标相等,
∴点与点之间的距离=1012-(-1011)=2023,
故选:A.
8.C
【分析】∠BEG=∠FEG-∠FEB=,∠AEF=180°-∠FEG-∠HEG=180°-2β,在△AEF中,,AD∥BC,∠D=∠ABC,得到AB∥CD,由平行线的性质和邻补角的定义即可求解.
【详解】解:设∠FBE=∠FEB=α,则∠AFE=2α,
∠FEH的角平分线为EG,设∠GEH=∠GEF=β,
∵AD∥BC,
∴∠ABC+∠BAD=180°,
∵∠D=∠ABC,
∴∠D+∠BAD=180°,
∴AB∥CD,
∵∠BEG=40°,
∴∠BEG=∠FEG-∠FEB=β-α=40°,
∵∠AEF=180°-∠FEG-∠HEG=180°-2β,
在△AEF中,180°-2β+2α+∠FAE=180°,
∴∠FAE=2β-2α=2(β-α)=80°,
∵AB∥CD,
∴∠CEH=∠FAE=80°,
∴∠DEH=180°-∠CEH=100°.
故选:C.
9.A
【分析】由△ABC的面积为18,根据三角形的面积公式和等积代换即可求得.
【详解】解:∵,
∴,
∵,,,
∴,
∴①,
同理,∵,,
∴,,
∴,
∴②,
由①-②得:.
故选:A.
10.D
【分析】甲出发3分钟后乙才出发,则AB段表示甲先出发3分钟内两人距离与甲出发时间的关系,故可得B点横坐标为3;BC段表示甲3分钟~6分钟内两人的距离与甲出发时间的关系,故可得点C横坐标为6;CD段两人距离不变,表示两人的速度相等,从而可得乙的速度为甲原来速度的,利用前6分钟的路程等于返回取物品的路程,可求得D点的横坐标,再利用相遇关系可求得第一次相遇的时间,从而也可求得甲最终达到B地的时间,从而确定答案.
【详解】由题意知:AB段表示甲先出发3分钟内两人距离与甲出发时间的关系,则;BC段表示甲3分钟~6分钟内两人的距离与甲出发时间的关系,故;CD段两人距离不变,表示两人的速度相等,从而可得乙的速度为甲原来速度的;设甲原来的速度为,提速后的速度为,则乙的速度为
甲行驶6分钟后,乙行驶3分钟,两人相距2320米,于是两人共行驶了4000 2320=1680()
则得方程:
解得:
则乙的速度为
故A正确
甲前3分钟的路程为:3×160=480(),3分钟时甲乙相距
故点B的坐标为
故C正确
设甲6分钟后返回的时间为
根据甲6分钟的路程=甲返回取回物品的路程,得方程:
解得:t=4
∴
即10后,甲乙均以速度相向而行,此时两人相距:,两人相遇的时间为:
所以甲出发到两人第一次相遇时间为:
故B正确
甲拿回物品后到达B地需要的时间为:,则甲最终达到B地所需的时间为:
故D错误
故选:D
二.填空题
11.(-3,-3)或(7,-3)##(7,-3)或(-3,-3)
【分析】根据平行于轴的直线是上的点的纵坐标相等求出点的纵坐标,再分点在点的左边与右边两种情况求出点的横坐标,即可得解.
【详解】解:∵轴轴,点的坐标为,
点的横坐标为,
,
点在点的左边时,横坐标为,
点在点的右边时,横坐标为,
点的坐标为或.
故答案为:或.
12.3
【分析】利用三角形的内角和定理,即可分别进行判断.
【详解】解:①∵,
又∵,
∴,
∴;故①符合题意;
②∵,
又;
∴,
∴;故②符合题意;
③∵,
又,
∴,
故③符合题意;
∴能确定为直角三角形的条件有3个;
故答案为:3.
13.或
【分析】先求出直线与坐标轴的交点坐标,再根据三角形的面积公式得到,求出k即可.
【详解】解:
当x=0时,y=10
∴与y轴交于点(0,10)
当y=0时,,
∴与x轴交于点,
∵围成的三角形的面积为5,
∴,
解得
∴该直线的表达式为或
故答案为:或.
14.1
【分析】根据题意求出的坐标,再根据,列出方程即可得出答案.
【详解】解:∵直线,直线的函数表达式为:,
∴设直线的函数表达式为:,
当时,,
∴,
∴,
∵,
∴,
∴,
把代入得:,
∴,
∴,
当时,,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵直线与正半轴交于点,
∴,
∴,
故答案为:.
15.
【分析】根据题意可知在时,有公共解,因此可以列出不等式,从而得到答案.
【详解】令,则,
令,则,
∵平移直线,可以使P、Q都在轴的下方,
∴可知在时,有公共解,
∴,解得:,
故填:.
16.
【分析】先根据角平分线的定义可得,,再根据四边形的内角和可得,然后根据三角形的外角性质即可得.
【详解】解:∵的角平分线与的外角平分线相交于点P,
∴,,
∵在四边形ABCD中,,
∴,
由三角形的外角性质得:,
.
故答案为:.
三.解答题
17.
(1)
如图所示:△A′B′C′即为所求;
(2)
由图可知,点,的坐标分别是:(0,4)(-1,1);
(3)
由图可知:,()
的面积为:.
18.
(1)
∵点P在一、三象限角平分线上,
∴.
∴,
∴,
∴点P的坐标;
(2)
∵点P的纵坐标比横坐标大5,
∴.
解得.
∴.
∴点P的坐标;
(3)
由题意知轴,
∴点A和点P的横坐标相同.
即,
解得.
∴.
∴点P的坐标为.
19.(1)解:,,
又,
,
,
,
.
,.
(2)解:∵三边长分别为a、b、c,
∴,,
∴|a+b﹣c|﹣|b﹣c﹣a|,
=a+b﹣c﹣(﹣b+c+a),
=a+b﹣c+b﹣a﹣c,
=2b﹣2c.
20.
(1)
把代入y=2x-2,
得2m-2=2,
解得m=2,
即m的值是2;
(2)
把,代入y=kx+b,
得,
解得,
∴直线的解析式为;
(3)
由图象可得,1<kx+b<2x-2的解集是2<x<3.
21.
(1)
解:直线过点,
,
,
点关于轴的对称点为点.
,
直线与直线平行,
设直线的解析式为,
代入得,,
解得,
直线的解析式为;
(2)
解:在直线中,令,则,
,
在直线中,令,则,
,
,,
,
设,
的面积是面积的,
,
,
,
或.
22.
(1)
解:设黄葛树的单价每棵a元,梧桐树的单价每棵b元,
由题意,得
,
解得:.
答:黄葛树的单价是每棵900元,梧桐树的单价是每棵700元.
(2)
解:①由题意,得
y=700x+900(84-x)
化简得y=-200x+75600
∴y与x之间的函数关系式为:y=-200x+75600;
②∵k=-200<0,
∴y随x的增大而减小.
∵x≤,
∴x≤28,
∴x=28时, =70000,
∴采购方案是:梧桐树采购28棵,黄葛树采购56棵,最少费用是70000元.
23.
(1)
解:根据题意得,AC=90km,BC=540km,
∴ km
故答案为:630;
(2)
解:∵货车从A地到C地行驶90km,用时2h,
∴货车的平均速度为: km/h,
∴行驶540km所用时间为:540÷45=12(h),
∴货车从A地出发到达B地所用时间为14h,
设货车从C到B的函数关系式为,
把(2,0)和(14,540)代入,得,
解得,
∴货车从C到B的函数关系式为;
(3)
解:设,
把(0,540)和(9,0)代入,得,
解得,
∴,
由题意可知:和的交点即为到C点距离相等,
联立方程组,
解得,
∴两车出发6小时,它们与C地的距离相等.
24.(1)
解:延长DB,交NC于点H,如图,
∵,,
∴,
∴.
∵,
∴.
∵,
∴.
∴;
(2)
解:延长DB,交NC于点H,如图,
∵,,
∴.∴.
∵,∴.
∵,∴,
∴.
∵BE平分,
∴.
∵,
∴.
∵BF平分,
∴.
∴;
(3)
解:∵,
∴.
∵CF平分,
∴.
∵,
∴.
∵,
∴.
∴.
由(2)知:.
∵,∴.
∴,
∴,
解得:.
∴,
∴.
25.
(1)
解:由函数图象可知,点M从A出发,从点C到D耗时秒,
,
此时,解得,
故答案为:12,16.
(2)
解:当点M在线段BC上运动时,,
设一次函数的解析式为,
将点代入得:,
解得,
∴.
(3)
解:当点M在BC上,即时,则,
解得,
当点M在CD上,即时,则,
解得,
∴,
∴在(1)的条件下,当时,等于10或.
(4)
解:由题意得,当Q运动到A停止的时间为,而点P运动到D的时间为,
(1)当点P、Q都在AD边上,此时有以PQ为底边,CD为高的三角形CPQ,
设运动的时间为t,则AP=2t,DQ=5t﹣16,
由得:,
,
①当点P在上方时,则PQ=AD﹣AP﹣QD=12﹣2t﹣5t+16=28﹣7t,
则△CPQ的面积为,解得,符合题意;
②当点P在点Q下方时,,
则△CPQ的面积为,解得,符合题意;
(2)当点P在CD上时,点Q运动到A时,则,
则△CPQ的面积为,解得,符合题意;
综上,的值为或或.
同课章节目录
