第十九章一次函数同步练习(含答案)2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 第十九章一次函数同步练习(含答案)2023-2024学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 477.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 14:41:48 | ||
图片预览



文档简介
第十九章一次函数同步练习 2023-2024学年 人教版数学八年级下册
一、单选题
1.甲以每小时20km的速度行驶时,他所走的路程S(km)与时间t(h)之间可用公式s=20t来表示,则下列说法正确的是( )
A.数20和s,t都是变量 B.s是常量,数20和t是变量
C.数20是常量,s和t是变量 D.t是常量,数20和s是变量
2.已知一次函数 的图象如图所示,则下列说法正确的是( )
A. , B. ,
C. , D. ,
3.下列各点在一次函数的图象上的是( )
A. B. C. D.
4.如图,函数和的图象相交于点,则关于x的不等式的解集是( )
A. B. C. D.
5.在函数中,自变量x的取值范围是( )
A.且 B.且
C. D.
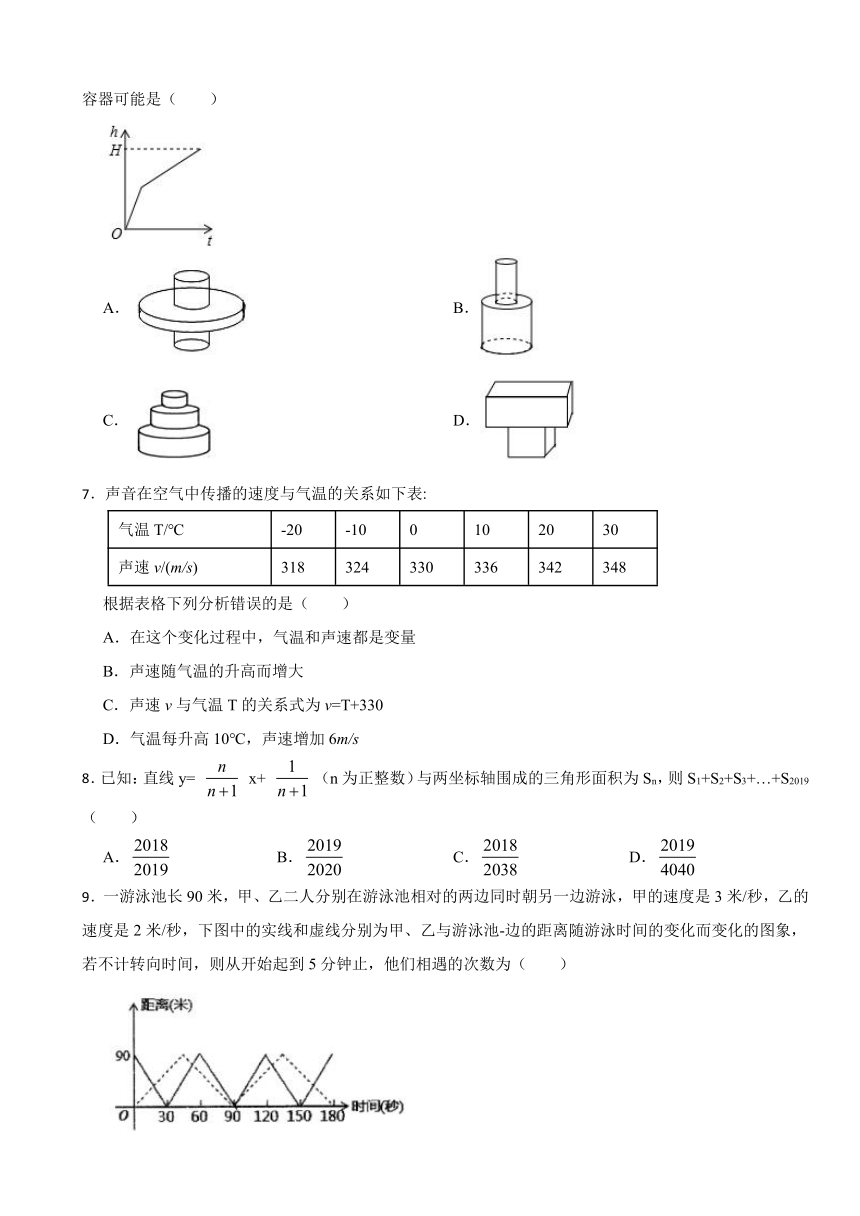
6.匀速地向一个容器内注水,在注满水的过程中,水面的高度h与时间t之间的函数关系如图所示,则该容器可能是( )
A. B.
C. D.
7.声音在空气中传播的速度与气温的关系如下表:
气温T/℃ -20 -10 0 10 20 30
声速v/(m/s) 318 324 330 336 342 348
根据表格下列分析错误的是( )
A.在这个变化过程中,气温和声速都是变量
B.声速随气温的升高而增大
C.声速v与气温T的关系式为v=T+330
D.气温每升高10℃,声速增加6m/s
8.已知:直线y= x+ (n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2019( )
A. B. C. D.
9.一游泳池长90米,甲、乙二人分别在游泳池相对的两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,下图中的实线和虚线分别为甲、乙与游泳池-边的距离随游泳时间的变化而变化的图象,若不计转向时间,则从开始起到5分钟止,他们相遇的次数为( )
A.8 B.7 C.6 D.5
10.如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )
A. B. +2 C. +2 D.
二、填空题
11.直线y=3x-6与x轴的交点坐标为 .
12.如图,直线y =x+b与y =kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是 .
13.如图,一次函数y=kx+b(k≠0)的图象如图所示,则关于x的不等式kx+b>2的解集应是 .
14.已知方程组 的解为 ,则一次函数y=2x+3与y=ax+c的图象的交点坐标是 .
15.小球从离地面为h(单位:m)的高处自由下落,落到地面所用时间为t(单位:s),经过实验,发现h与 成正比例关系,当 时, ,则当 时,t的值是 .
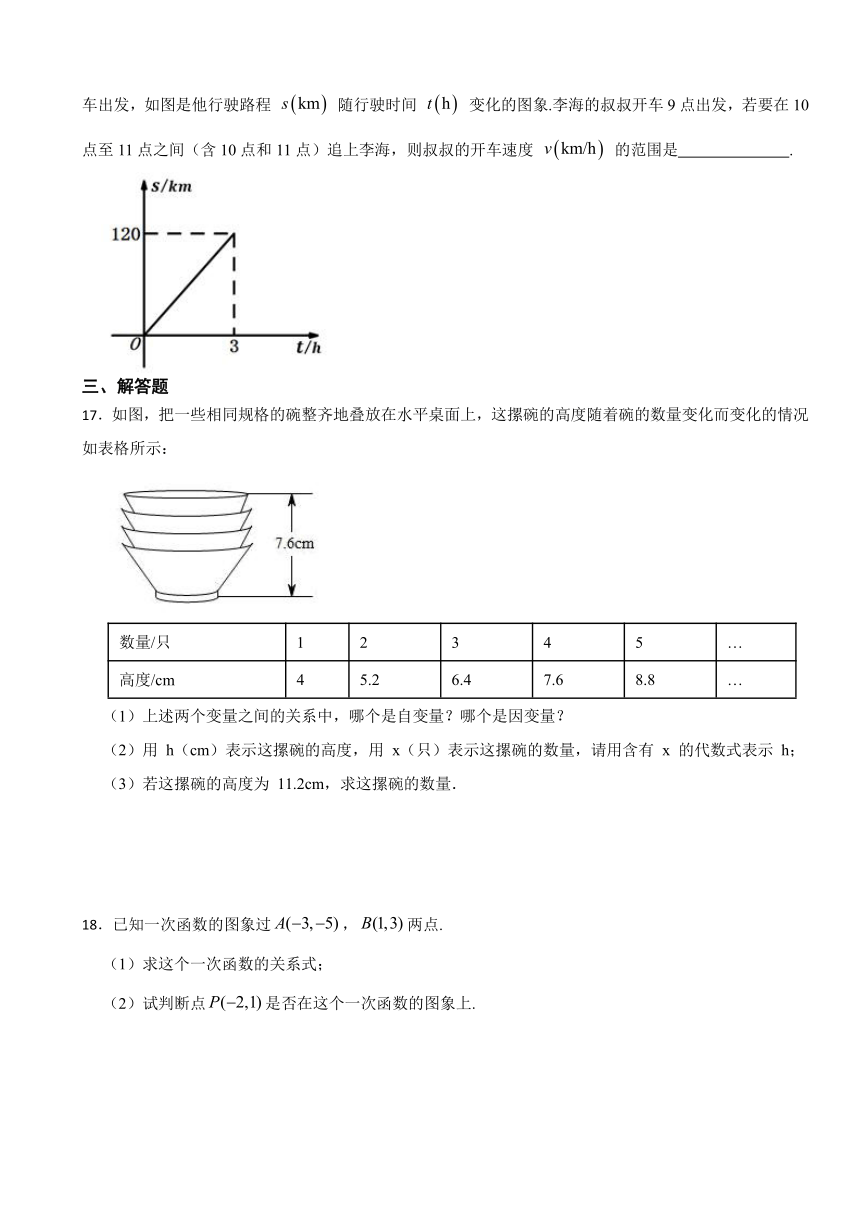
16.某个周末,李海和他的叔叔先后从家出发,他们沿着同一条公路匀速前往某景区,李海8点骑着电动车出发,如图是他行驶路程 随行驶时间 变化的图象.李海的叔叔开车9点出发,若要在10点至11点之间(含10点和11点)追上李海,则叔叔的开车速度 的范围是 .
三、解答题
17.如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
数量/只 1 2 3 4 5 …
高度/cm 4 5.2 6.4 7.6 8.8 …
(1)上述两个变量之间的关系中,哪个是自变量?哪个是因变量?
(2)用 h(cm)表示这摞碗的高度,用 x(只)表示这摞碗的数量,请用含有 x 的代数式表示 h;
(3)若这摞碗的高度为 11.2cm,求这摞碗的数量.
18.已知一次函数的图象过,两点.
(1)求这个一次函数的关系式;
(2)试判断点是否在这个一次函数的图象上.
19.如图,在平面直角坐标系中,一次函数的图象分别与轴交于两点,正比例函数的图象与交于点.
(1)求的值及的解析式;
(2)求的面积;
20.已知一次函数的图象经过点与.
(1)求这个一次函数的解析式;
(2)判断点是否在这个一次函数的图象上;
(3)直接写出关于的一元一次不等式的解.
21.如图,已知直线的图象经过点,,且与x轴交于点C.
(1)求直线的解析式;
(2)求的面积.
22.如图,直线 分别与x轴,y轴交于A B两点,A B的坐标分别为 、 ,过点B的直线 交x轴于点C,点 是直线l上的一点,连接 .
(Ⅰ)求 的解析式;
(Ⅱ)求C D的坐标;
(Ⅲ)求 的面积.
23.如图,在平面直角坐标系中,直线分别交x轴,y轴于点A、B.另一条直线与直线交于点,与x轴交于点,点P是直线上一点(不与点C重合).
(1)求a的值.
(2)当的面积为18时,求点P的坐标.
(3)若直线在平面直角坐标系内运动,且始终与平行,直线交直线于点M,交y轴于点N,当时,求的面积.
24.直线y=3x+3分别交x轴,y轴于点A,B,点D在x轴正半轴上,DC⊥AB于点C.
(1)直接写出点的坐标:A( ),B( );
(2)如图1,连接OC,若CO平分∠ACD,求直线CD的解析式;
(3)如图2,在(2)的条件下,点E在线段CD上运动,以OE为边作正方形OEFG(点O,E,F,G按逆时针排列)。
①求证:点G必在直线AB上;
②求证:点F在某条定直线上运动。
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】A
4.【答案】D
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】D
9.【答案】A
10.【答案】B
11.【答案】(2,0)
12.【答案】x>-1
13.【答案】x>2
14.【答案】
15.【答案】
16.【答案】
17.【答案】(1)碗的数量是自变量,高度是因变量;
(2)h=1.2x+2.8;
(3)7只;
18.【答案】(1).;(2)点不在这个一次函数图象上.
19.【答案】(1),直线的解析式为;
(2)20
20.【答案】(1)解:∵一次函数的图象经过点与,
∴,
解得,
∴这个一次函数的解析式为;
(2)解:当时,,
∴点在这个一次函数的图象上;
(3)解:∵,
∴函数中y随的增大而减小,
由(2)可得关于的一元一次不等式的解集为:.
21.【答案】(1)解:把点,分别代入直线的解析式,
得,,
解得,.
∴直线的解析式是.
(2)解:在直线中,令,得.
∴点C的坐标为.
∴.
22.【答案】解:(Ⅰ)设直线l1的解析式为y=kx+b,
把A(2,0)、B(0,3)代入得
,
解得 ,
∴直线l1的解析式为y=- x+3;
(Ⅱ)当y=0时, x+3=0,解得x=-6,
∴C点坐标为(-6,0),
把D(n,6)代入y=- x+3得- n+3=6,解得n=-2,
∴D点坐标为(-2,6);
(Ⅲ)S△BCD=S△DAC-S△BAC
= ×(2+6)×6- ×(2+6)×3
=12.
23.【答案】(1)5
(2)P的坐标为或
(3)
24.【答案】(1)-1,0;0,3
(2)解:设CD交y轴于点T,过点O分别作OM⊥AB于点M,ON⊥CD于点N,
证△BOM≌△DON,△AOB≌△TOD,
∴OD=OB=3,OT=OA=1,
∴T(0,1),D(3,0),
∴直线CD的解析式为
(3)解:如下图,过点E作EH⊥x轴于点H,过点G作GP⊥x轴于点P,过点F作FQ⊥EH交HE的延长线于点Q,证△OEH≌△GOP≌△EFQ,
设 ,则 .
①在y=3x+3中,令 ,则y=m-3+3=m,
∴点G在直线AB上;…12分
②令 ,消去参数m,得 ,
∴点F在定直线 上运动。……14分
一、单选题
1.甲以每小时20km的速度行驶时,他所走的路程S(km)与时间t(h)之间可用公式s=20t来表示,则下列说法正确的是( )
A.数20和s,t都是变量 B.s是常量,数20和t是变量
C.数20是常量,s和t是变量 D.t是常量,数20和s是变量
2.已知一次函数 的图象如图所示,则下列说法正确的是( )
A. , B. ,
C. , D. ,
3.下列各点在一次函数的图象上的是( )
A. B. C. D.
4.如图,函数和的图象相交于点,则关于x的不等式的解集是( )
A. B. C. D.
5.在函数中,自变量x的取值范围是( )
A.且 B.且
C. D.
6.匀速地向一个容器内注水,在注满水的过程中,水面的高度h与时间t之间的函数关系如图所示,则该容器可能是( )
A. B.
C. D.
7.声音在空气中传播的速度与气温的关系如下表:
气温T/℃ -20 -10 0 10 20 30
声速v/(m/s) 318 324 330 336 342 348
根据表格下列分析错误的是( )
A.在这个变化过程中,气温和声速都是变量
B.声速随气温的升高而增大
C.声速v与气温T的关系式为v=T+330
D.气温每升高10℃,声速增加6m/s
8.已知:直线y= x+ (n为正整数)与两坐标轴围成的三角形面积为Sn,则S1+S2+S3+…+S2019( )
A. B. C. D.
9.一游泳池长90米,甲、乙二人分别在游泳池相对的两边同时朝另一边游泳,甲的速度是3米/秒,乙的速度是2米/秒,下图中的实线和虚线分别为甲、乙与游泳池-边的距离随游泳时间的变化而变化的图象,若不计转向时间,则从开始起到5分钟止,他们相遇的次数为( )
A.8 B.7 C.6 D.5
10.如图,在平面直角坐标系中,点A在一次函数y= x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2 ,AD=1,则OD的最大值是( )
A. B. +2 C. +2 D.
二、填空题
11.直线y=3x-6与x轴的交点坐标为 .
12.如图,直线y =x+b与y =kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b>kx-1的解集是 .
13.如图,一次函数y=kx+b(k≠0)的图象如图所示,则关于x的不等式kx+b>2的解集应是 .
14.已知方程组 的解为 ,则一次函数y=2x+3与y=ax+c的图象的交点坐标是 .
15.小球从离地面为h(单位:m)的高处自由下落,落到地面所用时间为t(单位:s),经过实验,发现h与 成正比例关系,当 时, ,则当 时,t的值是 .
16.某个周末,李海和他的叔叔先后从家出发,他们沿着同一条公路匀速前往某景区,李海8点骑着电动车出发,如图是他行驶路程 随行驶时间 变化的图象.李海的叔叔开车9点出发,若要在10点至11点之间(含10点和11点)追上李海,则叔叔的开车速度 的范围是 .
三、解答题
17.如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
数量/只 1 2 3 4 5 …
高度/cm 4 5.2 6.4 7.6 8.8 …
(1)上述两个变量之间的关系中,哪个是自变量?哪个是因变量?
(2)用 h(cm)表示这摞碗的高度,用 x(只)表示这摞碗的数量,请用含有 x 的代数式表示 h;
(3)若这摞碗的高度为 11.2cm,求这摞碗的数量.
18.已知一次函数的图象过,两点.
(1)求这个一次函数的关系式;
(2)试判断点是否在这个一次函数的图象上.
19.如图,在平面直角坐标系中,一次函数的图象分别与轴交于两点,正比例函数的图象与交于点.
(1)求的值及的解析式;
(2)求的面积;
20.已知一次函数的图象经过点与.
(1)求这个一次函数的解析式;
(2)判断点是否在这个一次函数的图象上;
(3)直接写出关于的一元一次不等式的解.
21.如图,已知直线的图象经过点,,且与x轴交于点C.
(1)求直线的解析式;
(2)求的面积.
22.如图,直线 分别与x轴,y轴交于A B两点,A B的坐标分别为 、 ,过点B的直线 交x轴于点C,点 是直线l上的一点,连接 .
(Ⅰ)求 的解析式;
(Ⅱ)求C D的坐标;
(Ⅲ)求 的面积.
23.如图,在平面直角坐标系中,直线分别交x轴,y轴于点A、B.另一条直线与直线交于点,与x轴交于点,点P是直线上一点(不与点C重合).
(1)求a的值.
(2)当的面积为18时,求点P的坐标.
(3)若直线在平面直角坐标系内运动,且始终与平行,直线交直线于点M,交y轴于点N,当时,求的面积.
24.直线y=3x+3分别交x轴,y轴于点A,B,点D在x轴正半轴上,DC⊥AB于点C.
(1)直接写出点的坐标:A( ),B( );
(2)如图1,连接OC,若CO平分∠ACD,求直线CD的解析式;
(3)如图2,在(2)的条件下,点E在线段CD上运动,以OE为边作正方形OEFG(点O,E,F,G按逆时针排列)。
①求证:点G必在直线AB上;
②求证:点F在某条定直线上运动。
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】A
4.【答案】D
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】D
9.【答案】A
10.【答案】B
11.【答案】(2,0)
12.【答案】x>-1
13.【答案】x>2
14.【答案】
15.【答案】
16.【答案】
17.【答案】(1)碗的数量是自变量,高度是因变量;
(2)h=1.2x+2.8;
(3)7只;
18.【答案】(1).;(2)点不在这个一次函数图象上.
19.【答案】(1),直线的解析式为;
(2)20
20.【答案】(1)解:∵一次函数的图象经过点与,
∴,
解得,
∴这个一次函数的解析式为;
(2)解:当时,,
∴点在这个一次函数的图象上;
(3)解:∵,
∴函数中y随的增大而减小,
由(2)可得关于的一元一次不等式的解集为:.
21.【答案】(1)解:把点,分别代入直线的解析式,
得,,
解得,.
∴直线的解析式是.
(2)解:在直线中,令,得.
∴点C的坐标为.
∴.
22.【答案】解:(Ⅰ)设直线l1的解析式为y=kx+b,
把A(2,0)、B(0,3)代入得
,
解得 ,
∴直线l1的解析式为y=- x+3;
(Ⅱ)当y=0时, x+3=0,解得x=-6,
∴C点坐标为(-6,0),
把D(n,6)代入y=- x+3得- n+3=6,解得n=-2,
∴D点坐标为(-2,6);
(Ⅲ)S△BCD=S△DAC-S△BAC
= ×(2+6)×6- ×(2+6)×3
=12.
23.【答案】(1)5
(2)P的坐标为或
(3)
24.【答案】(1)-1,0;0,3
(2)解:设CD交y轴于点T,过点O分别作OM⊥AB于点M,ON⊥CD于点N,
证△BOM≌△DON,△AOB≌△TOD,
∴OD=OB=3,OT=OA=1,
∴T(0,1),D(3,0),
∴直线CD的解析式为
(3)解:如下图,过点E作EH⊥x轴于点H,过点G作GP⊥x轴于点P,过点F作FQ⊥EH交HE的延长线于点Q,证△OEH≌△GOP≌△EFQ,
设 ,则 .
①在y=3x+3中,令 ,则y=m-3+3=m,
∴点G在直线AB上;…12分
②令 ,消去参数m,得 ,
∴点F在定直线 上运动。……14分
