第十八章平行四边形同步练习(含答案)2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 第十八章平行四边形同步练习(含答案)2023-2024学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 596.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-26 14:42:24 | ||
图片预览

文档简介
第十八章平行四边形同步练习 2023-2024学年 人教版数学八年级下册
一、单选题
1.在中,,则的度数是( )
A. B. C. D.
2.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,长为半径画弧,两弧交于点D,分别连接,则四边形是平行四边形.其依据是( )
A.一组对边平行且相等的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.两组对边分别平行的四边形是平行四边形
D.一组对边平行,另一组对边相等的四边形是平行四边形
3.如图,在正方形中,点E,点F分别是对角线上的点,连接,,若,且,则的度数为( )
A.22.5° B.25° C.30° D.35°
4.如图,已知在 ABCD中,对角线AC,BD相交于点O,若AB=12,AC=16,BD=20,则△OCD的周长为( )
A.18 B.24 C.30 D.36
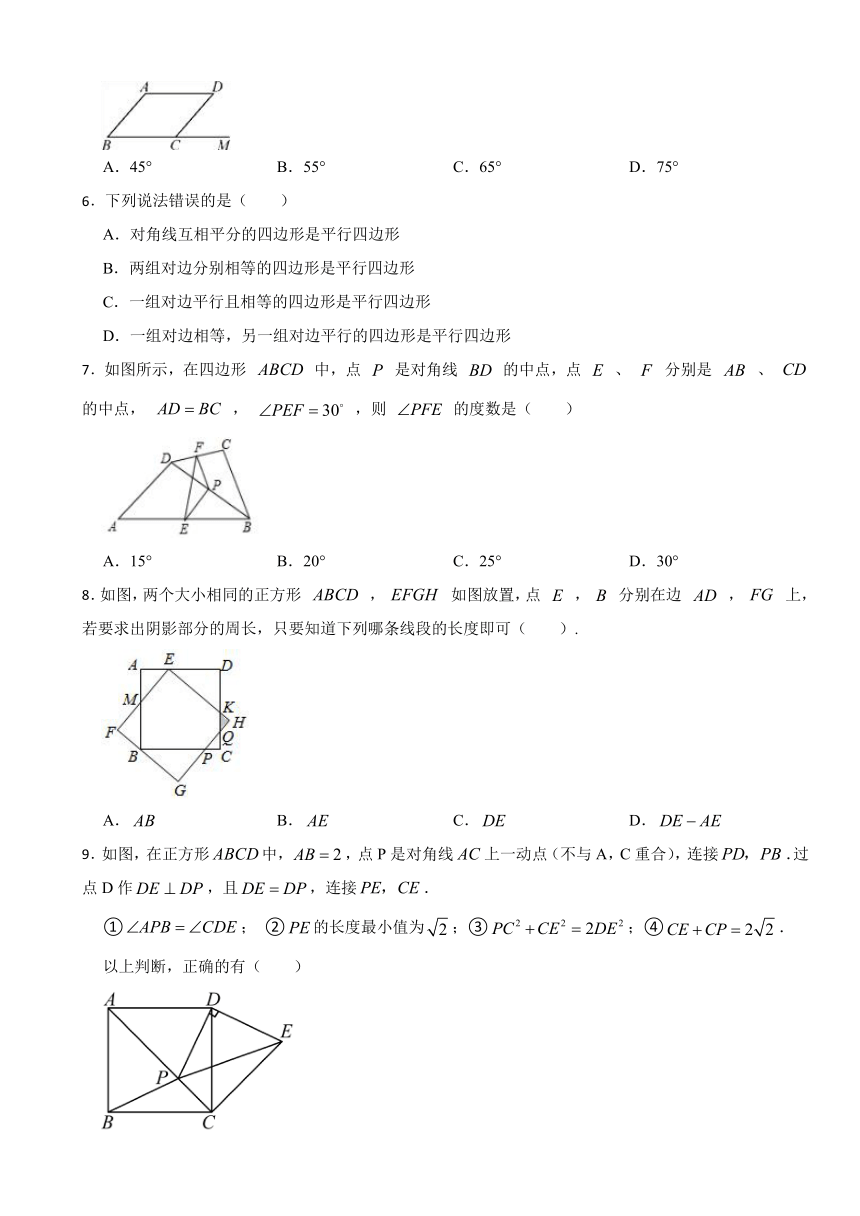
5.如图,在 ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A.45° B.55° C.65° D.75°
6.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
7.如图所示,在四边形 中,点 是对角线 的中点,点 、 分别是 、 的中点, , ,则 的度数是( )
A.15° B.20° C.25° D.30°
8.如图,两个大小相同的正方形 , 如图放置,点 , 分别在边 , 上,若要求出阴影部分的周长,只要知道下列哪条线段的长度即可( ).
A. B. C. D.
9.如图,在正方形中,,点P是对角线上一动点(不与A,C重合),连接.过点D作,且,连接.
①; ②的长度最小值为;③;④.
以上判断,正确的有( )
A.1个 B.2个 C.3个 D.4个
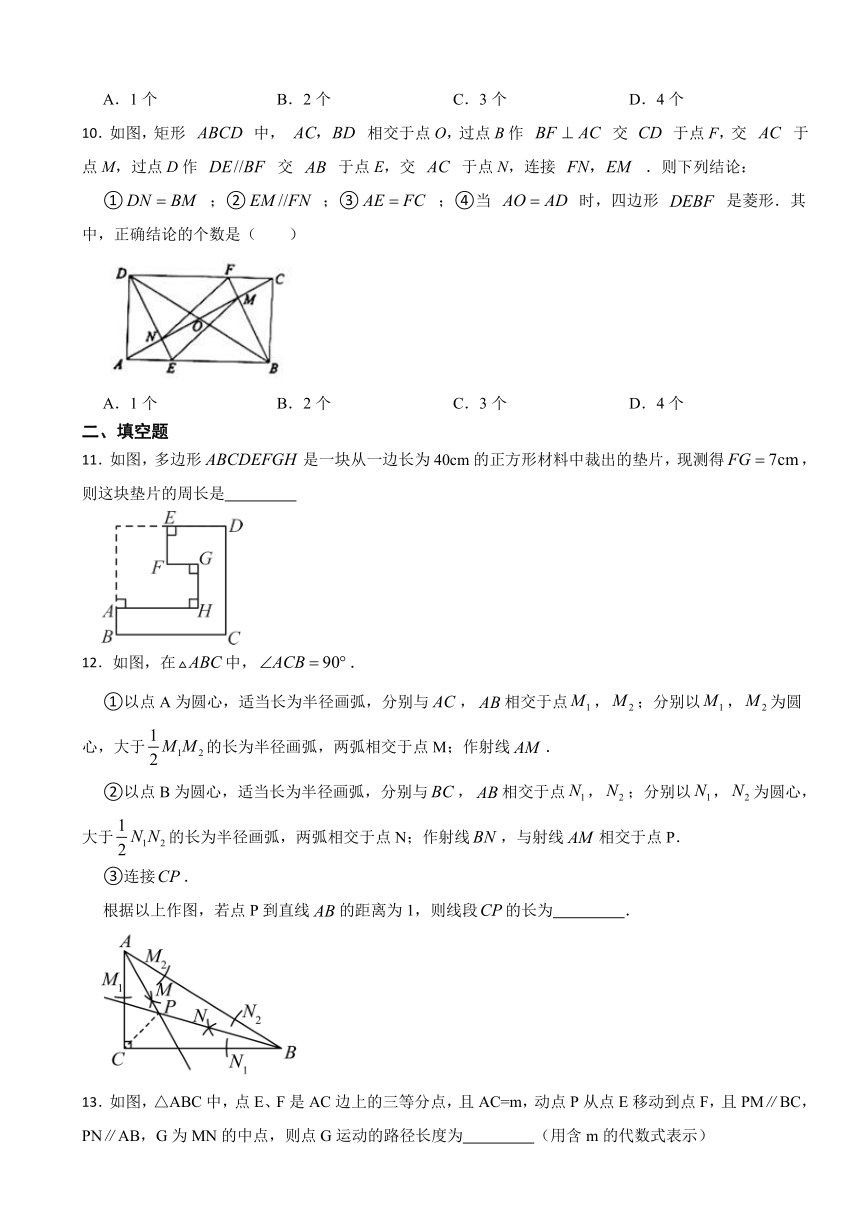
10.如图,矩形 中, 相交于点O,过点B作 交 于点F,交 于点M,过点D作 交 于点E,交 于点N,连接 .则下列结论:
① ;② ;③ ;④当 时,四边形 是菱形.其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,多边形是一块从一边长为40cm的正方形材料中裁出的垫片,现测得,则这块垫片的周长是
12.如图,在中,.
①以点A为圆心,适当长为半径画弧,分别与,相交于点,;分别以,为圆心,大于的长为半径画弧,两弧相交于点M;作射线.
②以点B为圆心,适当长为半径画弧,分别与,相交于点,;分别以,为圆心,大于的长为半径画弧,两弧相交于点N;作射线,与射线相交于点P.
③连接.
根据以上作图,若点P到直线的距离为1,则线段的长为 .
13.如图,△ABC中,点E、F是AC边上的三等分点,且AC=m,动点P从点E移动到点F,且PM∥BC,PN∥AB,G为MN的中点,则点G运动的路径长度为 (用含m的代数式表示)
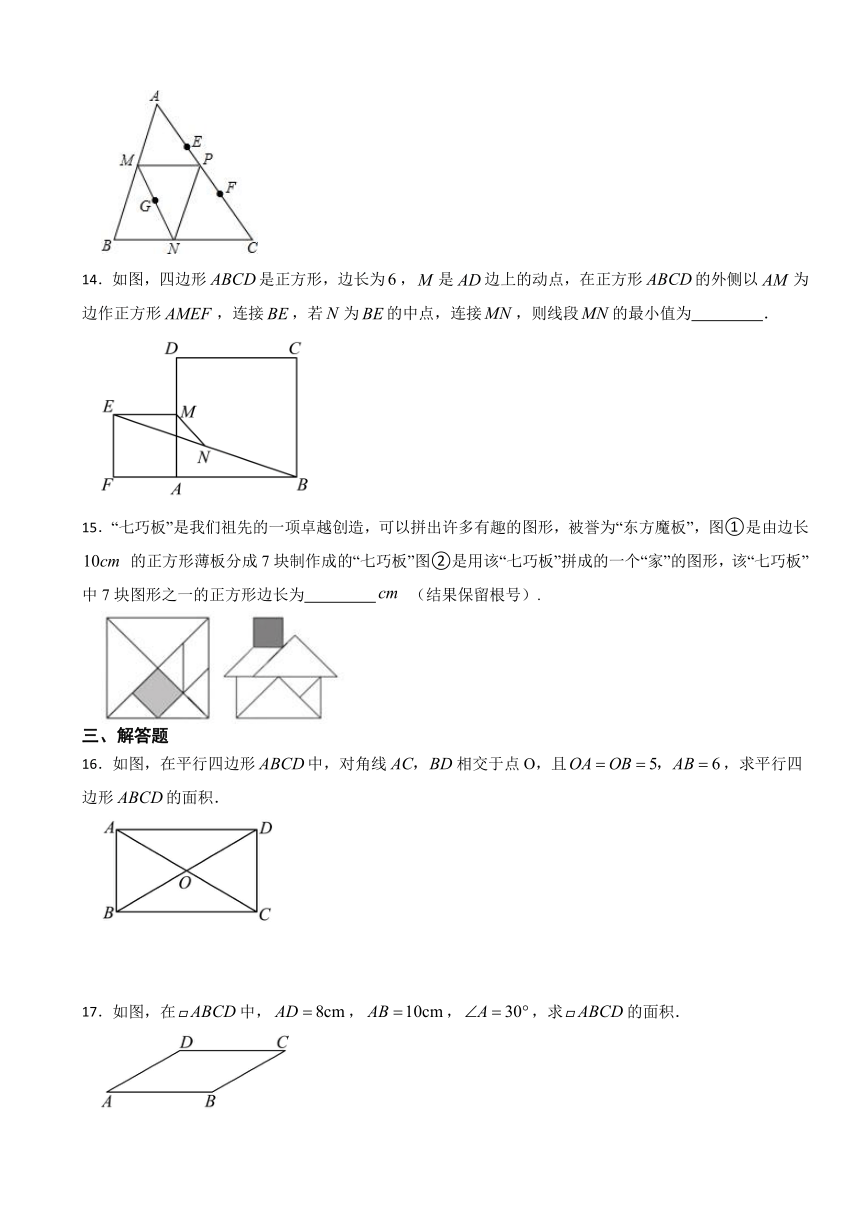
14.如图,四边形是正方形,边长为,是边上的动点,在正方形的外侧以为边作正方形,连接,若为的中点,连接,则线段的最小值为 .
15.“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”,图①是由边长 的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为 (结果保留根号).
三、解答题
16.如图,在平行四边形中,对角线相交于点O,且,求平行四边形的面积.
17.如图,在中,,,,求的面积.
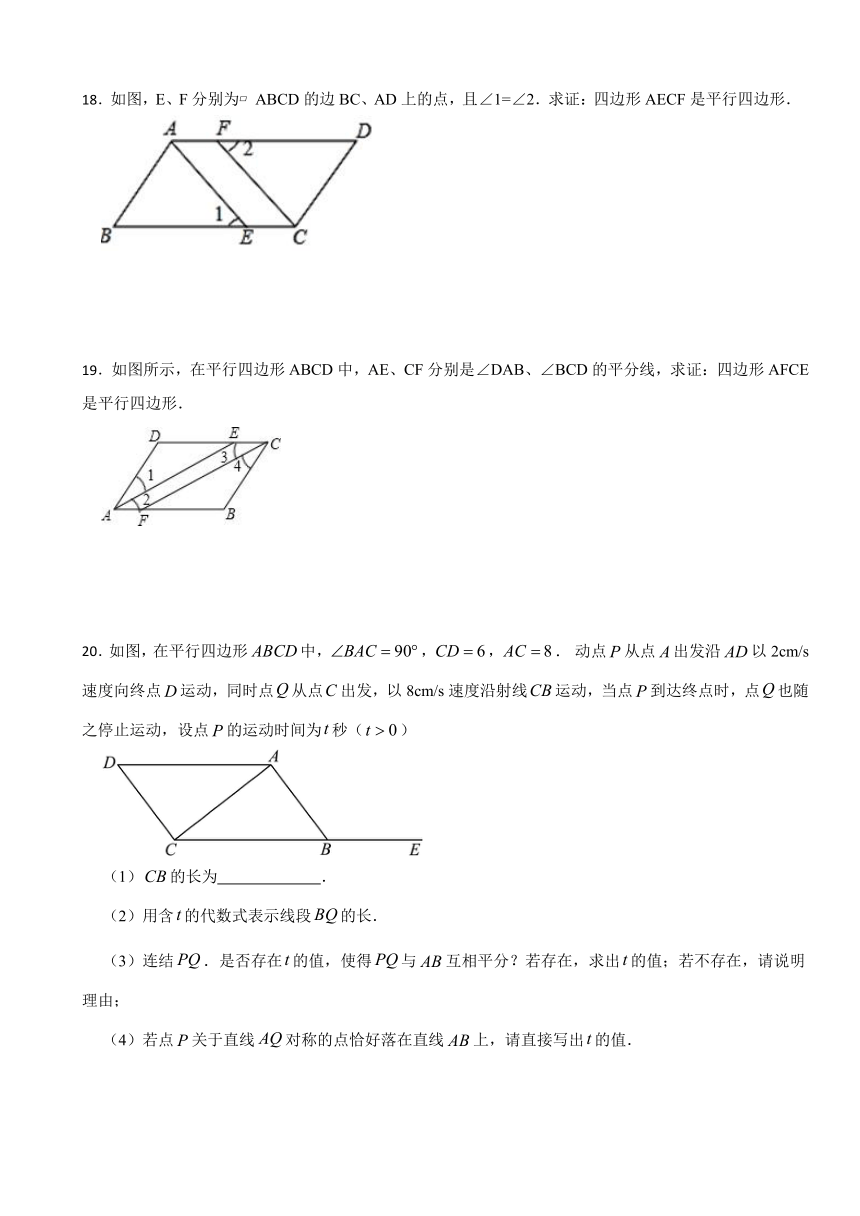
18.如图,E、F分别为 ABCD的边BC、AD上的点,且∠1=∠2.求证:四边形AECF是平行四边形.
19.如图所示,在平行四边形ABCD中,AE、CF分别是∠DAB、∠BCD的平分线,求证:四边形AFCE是平行四边形.
20.如图,在平行四边形中,,,. 动点从点出发沿以2cm/s速度向终点运动,同时点从点出发,以8cm/s速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒()
(1)的长为 .
(2)用含的代数式表示线段的长.
(3)连结.是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由;
(4)若点关于直线对称的点恰好落在直线上,请直接写出的值.
21.如图,菱形中,,E为边上一点,点F在的延长线上,,作点F关于直线的对称点G,连接.
(1)依题意补全图形,并证明;
(2)用等式表示之间的数量关系,并证明.
22.在中,,是BC的中点,是AD的中点,过点作交CE的延长线于点.
(1)求证:四边形ADBF是菱形;
(2)若,,求CF的长.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】A
6.【答案】D
7.【答案】D
8.【答案】C
9.【答案】C
10.【答案】D
11.【答案】174cm
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】48
17.【答案】的面积为
18.【答案】∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠1=∠EAF,
∵∠1=∠2,
∴∠EAF=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形.
19.【答案】证明:∵四边形ABCD是平行四边形,
∴CE∥AF,∠DAB=∠DCB,
∵AE、CF分别平分∠DAB、∠BCD,
∴∠2=∠3,
又∠3=∠CFB,
∴∠2=∠CFB,
∴AE∥CF,
又CE∥AF,
∴四边形AFCE是平行四边形.
20.【答案】(1)
(2)或
(3)存在,
(4)或
21.【答案】(1)解:补全的图形如图所示;
证明:∵菱形,
∴,
∴,
,
∴,
.
∵,
∴,
∴.
(2)解:之间的数量关系:.
证明:方法1
如图,连接.
∵菱形,,
∴,
∴为等边三角形,
∴,
点F关于的对称点G在线段上,
∴.
∵,
∴,
∴为等边三角形,
∴,
∴,
∴,
∴,
∴,
∴.
证明:方法2
如图,延长到H,使,
∴.
∵菱形,
∴.
又∵,
∴,
∴,
∴为等边三角形,
∴.
∵菱形,,点F关于直线的对称点为G,
∴点G在线段上,,
∴.
22.【答案】(1)证明:是BC的中点,是AD的中点,
,,
,,
在和中,
,,
,,四边形ADBF是平行四边形,
,D是BC的中点,,
四边形ADBF是菱形.
(2)解:作交CB的延长线于点,
则,
四边形ADBF是菱形,,
,,
和都是等边三角形,
,,
又,
,
,,
,
,
的长是.
一、单选题
1.在中,,则的度数是( )
A. B. C. D.
2.如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,长为半径画弧,两弧交于点D,分别连接,则四边形是平行四边形.其依据是( )
A.一组对边平行且相等的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.两组对边分别平行的四边形是平行四边形
D.一组对边平行,另一组对边相等的四边形是平行四边形
3.如图,在正方形中,点E,点F分别是对角线上的点,连接,,若,且,则的度数为( )
A.22.5° B.25° C.30° D.35°
4.如图,已知在 ABCD中,对角线AC,BD相交于点O,若AB=12,AC=16,BD=20,则△OCD的周长为( )
A.18 B.24 C.30 D.36
5.如图,在 ABCD中,M是BC延长线上的一点,若∠A=135°,则∠MCD的度数是( )
A.45° B.55° C.65° D.75°
6.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
7.如图所示,在四边形 中,点 是对角线 的中点,点 、 分别是 、 的中点, , ,则 的度数是( )
A.15° B.20° C.25° D.30°
8.如图,两个大小相同的正方形 , 如图放置,点 , 分别在边 , 上,若要求出阴影部分的周长,只要知道下列哪条线段的长度即可( ).
A. B. C. D.
9.如图,在正方形中,,点P是对角线上一动点(不与A,C重合),连接.过点D作,且,连接.
①; ②的长度最小值为;③;④.
以上判断,正确的有( )
A.1个 B.2个 C.3个 D.4个
10.如图,矩形 中, 相交于点O,过点B作 交 于点F,交 于点M,过点D作 交 于点E,交 于点N,连接 .则下列结论:
① ;② ;③ ;④当 时,四边形 是菱形.其中,正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,多边形是一块从一边长为40cm的正方形材料中裁出的垫片,现测得,则这块垫片的周长是
12.如图,在中,.
①以点A为圆心,适当长为半径画弧,分别与,相交于点,;分别以,为圆心,大于的长为半径画弧,两弧相交于点M;作射线.
②以点B为圆心,适当长为半径画弧,分别与,相交于点,;分别以,为圆心,大于的长为半径画弧,两弧相交于点N;作射线,与射线相交于点P.
③连接.
根据以上作图,若点P到直线的距离为1,则线段的长为 .
13.如图,△ABC中,点E、F是AC边上的三等分点,且AC=m,动点P从点E移动到点F,且PM∥BC,PN∥AB,G为MN的中点,则点G运动的路径长度为 (用含m的代数式表示)
14.如图,四边形是正方形,边长为,是边上的动点,在正方形的外侧以为边作正方形,连接,若为的中点,连接,则线段的最小值为 .
15.“七巧板”是我们祖先的一项卓越创造,可以拼出许多有趣的图形,被誉为“东方魔板”,图①是由边长 的正方形薄板分成7块制作成的“七巧板”图②是用该“七巧板”拼成的一个“家”的图形,该“七巧板”中7块图形之一的正方形边长为 (结果保留根号).
三、解答题
16.如图,在平行四边形中,对角线相交于点O,且,求平行四边形的面积.
17.如图,在中,,,,求的面积.
18.如图,E、F分别为 ABCD的边BC、AD上的点,且∠1=∠2.求证:四边形AECF是平行四边形.
19.如图所示,在平行四边形ABCD中,AE、CF分别是∠DAB、∠BCD的平分线,求证:四边形AFCE是平行四边形.
20.如图,在平行四边形中,,,. 动点从点出发沿以2cm/s速度向终点运动,同时点从点出发,以8cm/s速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒()
(1)的长为 .
(2)用含的代数式表示线段的长.
(3)连结.是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由;
(4)若点关于直线对称的点恰好落在直线上,请直接写出的值.
21.如图,菱形中,,E为边上一点,点F在的延长线上,,作点F关于直线的对称点G,连接.
(1)依题意补全图形,并证明;
(2)用等式表示之间的数量关系,并证明.
22.在中,,是BC的中点,是AD的中点,过点作交CE的延长线于点.
(1)求证:四边形ADBF是菱形;
(2)若,,求CF的长.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】C
5.【答案】A
6.【答案】D
7.【答案】D
8.【答案】C
9.【答案】C
10.【答案】D
11.【答案】174cm
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】48
17.【答案】的面积为
18.【答案】∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠1=∠EAF,
∵∠1=∠2,
∴∠EAF=∠2,
∴AE∥CF,
∴四边形AECF是平行四边形.
19.【答案】证明:∵四边形ABCD是平行四边形,
∴CE∥AF,∠DAB=∠DCB,
∵AE、CF分别平分∠DAB、∠BCD,
∴∠2=∠3,
又∠3=∠CFB,
∴∠2=∠CFB,
∴AE∥CF,
又CE∥AF,
∴四边形AFCE是平行四边形.
20.【答案】(1)
(2)或
(3)存在,
(4)或
21.【答案】(1)解:补全的图形如图所示;
证明:∵菱形,
∴,
∴,
,
∴,
.
∵,
∴,
∴.
(2)解:之间的数量关系:.
证明:方法1
如图,连接.
∵菱形,,
∴,
∴为等边三角形,
∴,
点F关于的对称点G在线段上,
∴.
∵,
∴,
∴为等边三角形,
∴,
∴,
∴,
∴,
∴,
∴.
证明:方法2
如图,延长到H,使,
∴.
∵菱形,
∴.
又∵,
∴,
∴,
∴为等边三角形,
∴.
∵菱形,,点F关于直线的对称点为G,
∴点G在线段上,,
∴.
22.【答案】(1)证明:是BC的中点,是AD的中点,
,,
,,
在和中,
,,
,,四边形ADBF是平行四边形,
,D是BC的中点,,
四边形ADBF是菱形.
(2)解:作交CB的延长线于点,
则,
四边形ADBF是菱形,,
,,
和都是等边三角形,
,,
又,
,
,,
,
,
的长是.
