6.1几何图形暑假预习练 人教版(2024)数学七年级上册
文档属性
| 名称 | 6.1几何图形暑假预习练 人教版(2024)数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 706.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-27 14:54:01 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
6.1几何图形
一、单选题
1.下列五种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;其中属于立体图形的是( )
A.①②③ B.③④⑤ C.③⑤ D.④⑤
2.将如图1所示的四棱锥沿着其中的四条棱剪开后,得到的展开图如图2所示,则剪开的四条棱可以为( )
A.,,, B.,,,
C.,,, D.,,,
3.下列图形是圆柱侧面展开图的是( )
A. B. C. D.
4.下列各图中,是正方体展开图的是( )
A. B. C. D.
5.下列说法不正确的是( )
A.长方体是四棱柱
B.八棱柱有8个面
C.六棱柱有12个顶点
D.经过棱柱的每个顶点有3条棱
6.如图,是一个几何体的主视图和左视图,则这个几何体可能为( )
A. B. C. D.
7.下列各组图形都是平面图形的一组是( )
A.线段、圆、圆锥、球 B.角、三角形、长方形、圆柱
C.长方体、圆柱、棱锥、球 D.圆、三角形、正方形、长方形
8.如下图所示将三角形绕直线l旋转一周,可以得到图(e)所示的立体图形的是( )
A.图(a) B.图(b) C.图(c) D.图(d)
9.用一个平面去截下列几何体,截得的平面图形可能是圆的有( )
A.0个 B.1个 C.2个 D.3个
10.下列说法正确的有( )
①五棱柱有10个顶点,10条棱,7个面;
②点动成线,线动成面,面动成体;
③圆锥的侧面展开图是一个圆;
④用平面去截一个正方体,截面的形状可以是三角形、四边形、五边形、六边形.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知圆柱的母线长是,侧面积是,则这个圆柱的底面半径是 .
12.在如图所示的展开图中,分别填上数字 1,2,3,4,5,6,使得折叠成正方体后,相对面上的 数字之和相等,则 a = b = , c = .
13.一个棱柱有6个面,则它的棱数是 .
14.如图是一个三棱柱的图形,它共有五个面,其中三个面是长方形,两个面是三角形,请写出符合下列条件的棱(说明:每个空只需写出一条即可).
(1)与棱BB1平行的棱: ;
(2)与棱BB1相交的棱: ;
(3)与棱BB1不在同一平面内的棱: .
15.四棱柱是由 个面围成的.
16.圆柱有 个面.
17.如图,下列几何体,是柱体的有 ,球体的有 .(填序号)
18.有一个正方体的六个面上分别标有数字,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字的面所对面上的数字记为, 的面所对面上数字记为,那么的值为 .
19.要做一个底面直径为acm,高为bcm的圆柱侧面模型,要剪裁的长方形纸片的面积为 .
20.下面有一张大图,这张大图的右下方有一块空白,是要填空的.填什么 ,请看大图右方若干个标有数码的小图.它们的大小、形状与右下角空白处一样.请将你要填的图的数码号写入空白处,使大图成为一张图形完整、协调一致的图.
三、解答题
21.某数学活动课上,进行制作长方体形状的包装盒子活动,现在利用边长为(cm)的正方形纸板制作出了两种方案的长方体盒子(图1是无盖的长方体纸盒,图2是有盖的长方体纸盒)
(1)先在正方形纸板的四个角处剪去四个边长为(cm)的小正方形,再沿虚线折合起来,得到无盖的长方形盒子,则
①长方体盒子的高为:________cm;
②盒子的底面面积为:________;
(2)先在正方形纸板的相邻两角剪去边长均为(cm)的两个小正方形,再在剩下的正方形两个角处剪去两个同样大小一边长为(cm)的小长方形,最后沿虚线折合起来,得到有盖的长方体盒子.若,,求长方体盒子的体积.
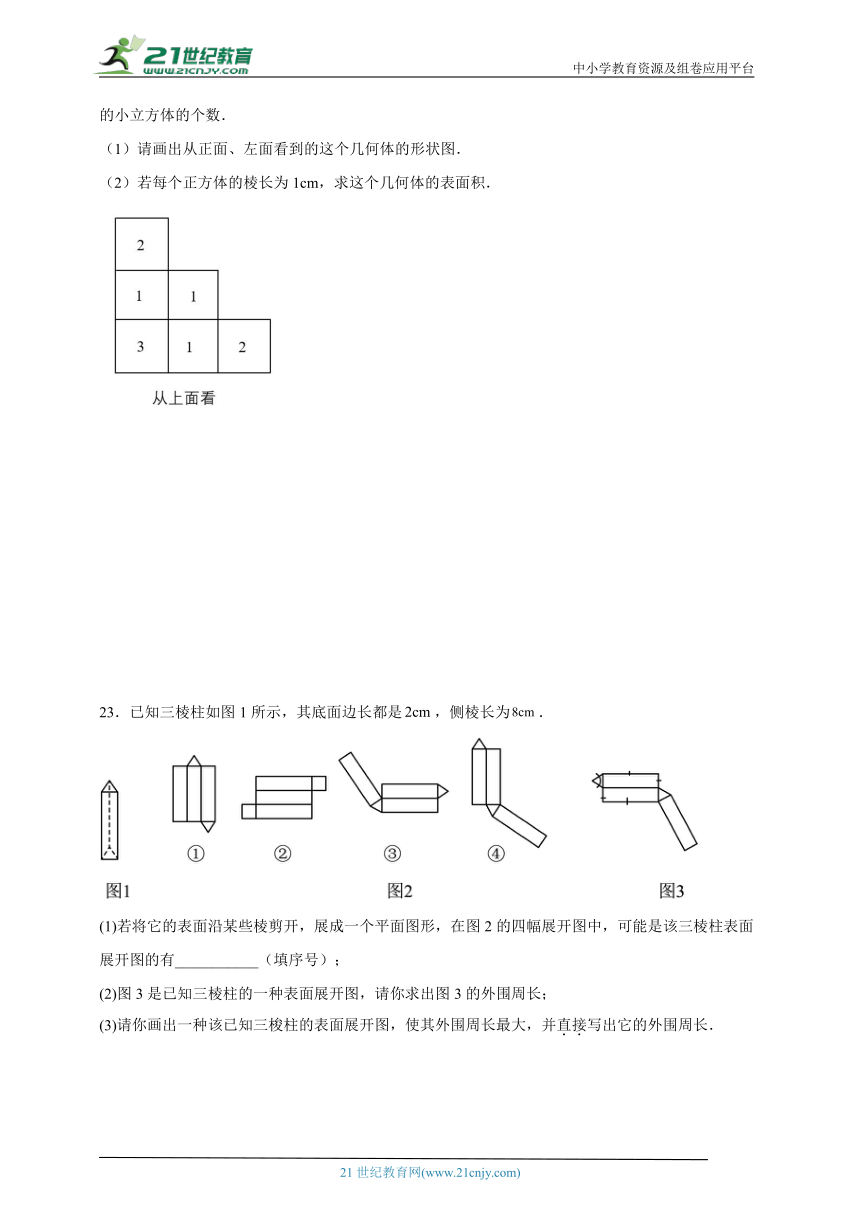
22.由几个小立方体搭成的几何体从上面看得到的形状图如图所示,小正方形中的数字表示在该位置的小立方体的个数.
(1)请画出从正面、左面看到的这个几何体的形状图.
(2)若每个正方体的棱长为1cm,求这个几何体的表面积.
23.已知三棱柱如图1所示,其底面边长都是,侧棱长为.
(1)若将它的表面沿某些棱剪开,展成一个平面图形,在图2的四幅展开图中,可能是该三棱柱表面展开图的有___________(填序号);
(2)图3是已知三棱柱的一种表面展开图,请你求出图3的外围周长;
(3)请你画出一种该已知三梭柱的表面展开图,使其外围周长最大,并直接写出它的外围周长.
24.左图是由6个大小相同的正方体组成的立体图形,图①、图②、图③均为3×3的正方形网格.在图①、图②、图③中分别画出左图所示立体图形的三视图.
25.如图所示的三个图形经过折叠都能围成棱柱吗?先想一想,再折一折.并说出能围成的棱柱的名称.
参考答案:
1.B
【分析】根据立体图形与平面图形的定义即可解答.
【详解】①长方形是平面图形,
②梯形是平面图形,
③正方体是立体图形,
④圆柱是立体图形,
⑤圆锥是立体图形,
所以,属于立体图形的是③④⑤.
故选:B.
本题考查平面图形与立体图形的认识,理解平面图形与立体图形的概念是解答本题的关键.
2.A
【分析】根据四棱锥的展开图特点即可判断.
【详解】由四棱锥的展开图可知,需剪开两条侧棱与两条底面的棱,
并且侧棱需剪掉共点顶点,底面为相对的棱,
故A正确;
此题主要考查四棱锥的展开图,解题的关键是熟知根据四棱锥的展开图的特点.
3.D
【分析】本题考查了几何体的展开图,对几何体的正确认识以及运用空间想象能力是解题的关键.
【详解】解:根据题意,把圆柱的侧面沿它的一条母线剪开展在一个平面上,
得到其侧面展开图是对边平行且相等的四边形;
又有母线垂直于上下底面,故可得是长方形.
故选:D.
4.C
【分析】根据正方体展开图的11种特征,图结构,是正方体的展开图;图B、图C和图D不符合正方体展开图的11种特征,不是正方体的展开图.
【详解】解:根据正方体展开图的11种特征,图结构,是正方体的展开图;
故选:C.
本题是考查正方体的展开图,正方体展开图有11种特征,分四种类型,即:第一种:结构,即第一行放1个,第二行放4个,第三行放1个;第二种:结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:结构,即每一行放3个正方形,只有一种展开图;第四种:结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.
5.B
【分析】根据四、六、八棱柱的特点可得答案.
【详解】解:A、长方体是四棱柱,选项说法正确,不符合题意;
B、八棱柱有8+2=10个面,选项说法错误,符合题意;
C、六棱柱有2×6=12个顶点,选项说法正确,不符合题意;
D、经过棱柱的每个顶点有3条棱,选项说法正确,不符合题意;
故选:B.
此题主要考查了认识立体图形,关键是认识常见的立体图形,掌握棱柱、棱锥、圆柱、圆锥的特点.
6.B
【分析】分别画出各个几何体的主视图和左视图,再判断即可.
【详解】解:分别画出各个几何体的主视图和左视图,
故选B.
本题主要考查了几何体的主视图和左视图,准确的画出各几何体的主视图和左视图是解决本题的关键.
7.D
【分析】根据平面图形定义:一个图形的各部分都在同一个平面内的图形是平面图形可得答案.
【详解】解:A.圆锥、球是立体图形,不是平面图形,故此选项错误;
B.圆柱是立体图形,不是平面图形,故此选项错误;
C.长方体、圆柱、棱锥、球都是立体图形,不是平面图形,故此选项错误;
D.圆、三角形、正方形、长方形都是平面图形,故此选项正确.
故选D.
此题主要考查了平面图形,关键是掌握平面图形的定义.
8.B
【分析】由题意根据一个平面图形围绕一条边为中心对称轴旋转一周根据面动成体的原理进行分析即可.
【详解】解:绕直角三角形一条直角边旋转可得到圆锥.
本题要求得到两个圆锥的组合体,那么一定是两个直角三角形的组合体:两条直角边相对,绕另一直角边旋转而成的.
故选:B.
本题考查面动成体,注意掌握可以把较复杂的体分解熟悉的立体图形来进行分析.
9.C
【分析】本题考查了截一个几何体,根据三棱柱,圆锥,圆柱,四棱柱的特点判断即可.
【详解】解:三棱柱,四棱柱的截面不可能是圆,圆锥,圆柱的截面可能是圆,
故选:C.
10.B
【分析】本题考查简单的几何图形具有的特点,根据立体图形的特征,点、线、面、体,圆锥的特征和截一个几何体的方法判断即可.
【详解】解:①五棱柱有10个顶点,15条棱,7个面,所以①错误,不符合题意.
②点动成线,线动成面,面动成体,所以②正确,符合题意.
③圆锥的侧面展开图是一个扇形,所以③错误,不符合题意.
④用平面去截一个正方体,截面的形状可以是三角形、四边形、五边形、六边形,所以④正确,符合题意.
综上所述,说法正确的有2个,
故选:B.
11.
【分析】∵圆柱侧面积=底面周长×高,∴底面半径=底面周长÷2π=圆柱侧面积÷高÷2π.
【详解】解:根据圆柱的侧面积公式可得这个圆柱的底面半径==2(cm).
故答案为2.
本题主要考查了圆柱的侧面积的计算方法.
12. 6 2 4
【详解】试题分析:首先找出正方体相对的面,然后进行计算.根据题意可得:5+b=1+a=3+c,则a=6,b=2,c=4.
考点:正方体的展开图
13.12
【分析】根据n棱柱的特点,由n个侧面和两个底面构成,可得该棱柱是四棱柱,由此即可解答.
【详解】解:由题意可知:6-2=4,
故该棱柱是四棱柱,它的棱数是12.
故答案为:12.
本题主要考查了棱柱的概念,根据棱柱的底面和侧面的关系求解是解题关键.
14. AA1; A1B1; AC;
【分析】在长方体中,棱与棱之间有平行,相交(垂直)和异面等关系,即可得出结果.
【详解】解:(1)与棱BB1 平行的棱是AA1,
故答案为:AA1;
(2)与棱BB1相交的棱是A1 B1,
故答案为:A1B1;
(3)与棱BB1不在同一平面内的棱是AC,
故答案为:AC.
本题考查了立体图形的有关概念;熟记棱与棱之间有平行,相交(垂直)和异面等关系是解决问题的关键.
15.6
【分析】根据四棱柱有两个底面,四个侧面,即可解答.
【详解】解:∵四棱柱有两个底面,四个侧面,,
∴四棱柱是由6个面围成.
故答案为:6.
16.3/三
【分析】根据圆柱的几何特征求解即可.
【详解】解:∵圆柱有上下两个底面,一个侧面,
∴圆柱有3个面,
故答案为:3.
本题考查圆柱,熟知常见几何体的几何特征是解答的关键.
17. ①②⑥ ⑤
【分析】根据立体图形的特征即可得到答案.
【详解】解:柱体的有①②⑥;球体有⑤.
故答案为:①②⑥,⑤
本题考查了认识立体图形,熟知立体图形的特征并知道他们的名称是解题关键.
18.
【分析】本题考查了运用正方体的相对面解答问题,根据与相邻的面的数字有判断出的对面数字是,与相邻的面的数字有判断出4的对面数字是,从而确定出的对面数字是,然后确定出的值,相加即可求解,正确判断对面和邻面是解题的关键.
【详解】解:由图可知,
∵与相邻的面的数字有,
∴的对面数字是,
∵与相邻的面的数字有,
∴的对面数字是,
∴的对面数字是,
∵标有数字的面所对面上的数字记为,的面所对面上数字记为,
∴,,
∴,
故答案为:.
19.πabcm2
【分析】长方形纸片的面积就是圆柱的侧面积,圆柱侧面积=底面周长×高.
【详解】长方形纸片的面积=π×ab=abπ.
则答案为abπcm2.
本题考查了圆柱的相关知识,解题的关键是熟练的掌握圆柱的侧面积公式与运算.
20.8
【分析】观察图形的特征,每一行的图案一样,即可得到答案.
【详解】观察得知,每一行的图形是一样的,第三行的图案均应该是三个圆圈,与8中的图案一样,
故答案为:8.
认识平面图形,找准图形中的规律是解题关键.
21.(1)①,②;
(2)长方体盒子的体积
【分析】本题考查了简单几何体的展开图,熟练根据简单几何的展开图得出长方体的长宽高是解题的关键.
(1)根据长方形面积公式得出答案即可;
(2)根据长方体公式得出答案即可.
【详解】(1)解:①由题意可知,盒子的高为.
②盒子的边长为,
∴盒子的底面面积为.
(2)解:由题意可知,该长方体的底面积为,
∴长方体的体积为,
把,代入可得,
.
22.(1)见解析;(2)
【分析】(1)由已知条件可知,从正面看有3列,每列小正方形的数目分别为;从左面看有3列,每列小正方形的数目分别为;据此画出图形;
(2)根据几何体三个方向看到的图形可求出几何体的表面积.
【详解】解:(1)如图所示:
;
(2),
答:该几何体的表面积为.
本题考查从不同方向看几何体.以及几何体的表面积,由几何体的从上面看到的形状及小正方形内的数字,可知左面的列数与上面的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左面的列数与上面的行数相同,且每列小正方形数目为上面看到的图中相应行中正方形数字中的最大数字.
23.(1)①④
(2)
(3),图见解析
【分析】(1)根据三棱柱的特点求解即可;
(2)结合图形利用棱长计算周长即可;
(3)要使得外围的周长最大,使得漏在外面的侧棱最多即可.
【详解】(1)解:根据三棱柱的特点可得①④为展开图,
故答案为:①④;
(2)图3的外围周长为
(3)图形不唯一,例如:
最大周长为:.
本题主要考查三棱柱的展开图及周长的计算,熟练掌握立体图形的展开图特点是解题关键.
24.见详解
【分析】本题考查了从不同方向看几何体;
从正面看有3列,左侧有3个正方形,中间有1个正方形,右侧有1个正方形;从左边看有2列,左侧有3个正方形,右侧有1个正方形;从上面看有3列,左侧有1个正方形,中间有2个正方形,右侧有1个正方形;
【详解】解:如图
25.都能围成棱柱,依次为四棱柱(长方体),五棱柱,三棱柱.
【分析】本题是操作问题,可以尝试操作,或想象操作.根据棱柱的特征,特别是侧面和上下两个底面的位置特征作答.
【详解】第一个图形可以围成直四棱柱;
第二个图折叠后可以围成五棱柱;
第三个图形,将两个长方形往中间的那个面折叠,即可得一三棱柱.可以折成三棱柱.
本题考查了展开图折叠成几何体,熟练掌握常见立体图形的平面展开图的特征,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.1几何图形
一、单选题
1.下列五种图形:①长方形;②梯形;③正方体;④圆柱;⑤圆锥;其中属于立体图形的是( )
A.①②③ B.③④⑤ C.③⑤ D.④⑤
2.将如图1所示的四棱锥沿着其中的四条棱剪开后,得到的展开图如图2所示,则剪开的四条棱可以为( )
A.,,, B.,,,
C.,,, D.,,,
3.下列图形是圆柱侧面展开图的是( )
A. B. C. D.
4.下列各图中,是正方体展开图的是( )
A. B. C. D.
5.下列说法不正确的是( )
A.长方体是四棱柱
B.八棱柱有8个面
C.六棱柱有12个顶点
D.经过棱柱的每个顶点有3条棱
6.如图,是一个几何体的主视图和左视图,则这个几何体可能为( )
A. B. C. D.
7.下列各组图形都是平面图形的一组是( )
A.线段、圆、圆锥、球 B.角、三角形、长方形、圆柱
C.长方体、圆柱、棱锥、球 D.圆、三角形、正方形、长方形
8.如下图所示将三角形绕直线l旋转一周,可以得到图(e)所示的立体图形的是( )
A.图(a) B.图(b) C.图(c) D.图(d)
9.用一个平面去截下列几何体,截得的平面图形可能是圆的有( )
A.0个 B.1个 C.2个 D.3个
10.下列说法正确的有( )
①五棱柱有10个顶点,10条棱,7个面;
②点动成线,线动成面,面动成体;
③圆锥的侧面展开图是一个圆;
④用平面去截一个正方体,截面的形状可以是三角形、四边形、五边形、六边形.
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知圆柱的母线长是,侧面积是,则这个圆柱的底面半径是 .
12.在如图所示的展开图中,分别填上数字 1,2,3,4,5,6,使得折叠成正方体后,相对面上的 数字之和相等,则 a = b = , c = .
13.一个棱柱有6个面,则它的棱数是 .
14.如图是一个三棱柱的图形,它共有五个面,其中三个面是长方形,两个面是三角形,请写出符合下列条件的棱(说明:每个空只需写出一条即可).
(1)与棱BB1平行的棱: ;
(2)与棱BB1相交的棱: ;
(3)与棱BB1不在同一平面内的棱: .
15.四棱柱是由 个面围成的.
16.圆柱有 个面.
17.如图,下列几何体,是柱体的有 ,球体的有 .(填序号)
18.有一个正方体的六个面上分别标有数字,从三个不同的角度观察这个正方体所得到的结果如图所示,如果标有数字的面所对面上的数字记为, 的面所对面上数字记为,那么的值为 .
19.要做一个底面直径为acm,高为bcm的圆柱侧面模型,要剪裁的长方形纸片的面积为 .
20.下面有一张大图,这张大图的右下方有一块空白,是要填空的.填什么 ,请看大图右方若干个标有数码的小图.它们的大小、形状与右下角空白处一样.请将你要填的图的数码号写入空白处,使大图成为一张图形完整、协调一致的图.
三、解答题
21.某数学活动课上,进行制作长方体形状的包装盒子活动,现在利用边长为(cm)的正方形纸板制作出了两种方案的长方体盒子(图1是无盖的长方体纸盒,图2是有盖的长方体纸盒)
(1)先在正方形纸板的四个角处剪去四个边长为(cm)的小正方形,再沿虚线折合起来,得到无盖的长方形盒子,则
①长方体盒子的高为:________cm;
②盒子的底面面积为:________;
(2)先在正方形纸板的相邻两角剪去边长均为(cm)的两个小正方形,再在剩下的正方形两个角处剪去两个同样大小一边长为(cm)的小长方形,最后沿虚线折合起来,得到有盖的长方体盒子.若,,求长方体盒子的体积.
22.由几个小立方体搭成的几何体从上面看得到的形状图如图所示,小正方形中的数字表示在该位置的小立方体的个数.
(1)请画出从正面、左面看到的这个几何体的形状图.
(2)若每个正方体的棱长为1cm,求这个几何体的表面积.
23.已知三棱柱如图1所示,其底面边长都是,侧棱长为.
(1)若将它的表面沿某些棱剪开,展成一个平面图形,在图2的四幅展开图中,可能是该三棱柱表面展开图的有___________(填序号);
(2)图3是已知三棱柱的一种表面展开图,请你求出图3的外围周长;
(3)请你画出一种该已知三梭柱的表面展开图,使其外围周长最大,并直接写出它的外围周长.
24.左图是由6个大小相同的正方体组成的立体图形,图①、图②、图③均为3×3的正方形网格.在图①、图②、图③中分别画出左图所示立体图形的三视图.
25.如图所示的三个图形经过折叠都能围成棱柱吗?先想一想,再折一折.并说出能围成的棱柱的名称.
参考答案:
1.B
【分析】根据立体图形与平面图形的定义即可解答.
【详解】①长方形是平面图形,
②梯形是平面图形,
③正方体是立体图形,
④圆柱是立体图形,
⑤圆锥是立体图形,
所以,属于立体图形的是③④⑤.
故选:B.
本题考查平面图形与立体图形的认识,理解平面图形与立体图形的概念是解答本题的关键.
2.A
【分析】根据四棱锥的展开图特点即可判断.
【详解】由四棱锥的展开图可知,需剪开两条侧棱与两条底面的棱,
并且侧棱需剪掉共点顶点,底面为相对的棱,
故A正确;
此题主要考查四棱锥的展开图,解题的关键是熟知根据四棱锥的展开图的特点.
3.D
【分析】本题考查了几何体的展开图,对几何体的正确认识以及运用空间想象能力是解题的关键.
【详解】解:根据题意,把圆柱的侧面沿它的一条母线剪开展在一个平面上,
得到其侧面展开图是对边平行且相等的四边形;
又有母线垂直于上下底面,故可得是长方形.
故选:D.
4.C
【分析】根据正方体展开图的11种特征,图结构,是正方体的展开图;图B、图C和图D不符合正方体展开图的11种特征,不是正方体的展开图.
【详解】解:根据正方体展开图的11种特征,图结构,是正方体的展开图;
故选:C.
本题是考查正方体的展开图,正方体展开图有11种特征,分四种类型,即:第一种:结构,即第一行放1个,第二行放4个,第三行放1个;第二种:结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:结构,即每一行放3个正方形,只有一种展开图;第四种:结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.
5.B
【分析】根据四、六、八棱柱的特点可得答案.
【详解】解:A、长方体是四棱柱,选项说法正确,不符合题意;
B、八棱柱有8+2=10个面,选项说法错误,符合题意;
C、六棱柱有2×6=12个顶点,选项说法正确,不符合题意;
D、经过棱柱的每个顶点有3条棱,选项说法正确,不符合题意;
故选:B.
此题主要考查了认识立体图形,关键是认识常见的立体图形,掌握棱柱、棱锥、圆柱、圆锥的特点.
6.B
【分析】分别画出各个几何体的主视图和左视图,再判断即可.
【详解】解:分别画出各个几何体的主视图和左视图,
故选B.
本题主要考查了几何体的主视图和左视图,准确的画出各几何体的主视图和左视图是解决本题的关键.
7.D
【分析】根据平面图形定义:一个图形的各部分都在同一个平面内的图形是平面图形可得答案.
【详解】解:A.圆锥、球是立体图形,不是平面图形,故此选项错误;
B.圆柱是立体图形,不是平面图形,故此选项错误;
C.长方体、圆柱、棱锥、球都是立体图形,不是平面图形,故此选项错误;
D.圆、三角形、正方形、长方形都是平面图形,故此选项正确.
故选D.
此题主要考查了平面图形,关键是掌握平面图形的定义.
8.B
【分析】由题意根据一个平面图形围绕一条边为中心对称轴旋转一周根据面动成体的原理进行分析即可.
【详解】解:绕直角三角形一条直角边旋转可得到圆锥.
本题要求得到两个圆锥的组合体,那么一定是两个直角三角形的组合体:两条直角边相对,绕另一直角边旋转而成的.
故选:B.
本题考查面动成体,注意掌握可以把较复杂的体分解熟悉的立体图形来进行分析.
9.C
【分析】本题考查了截一个几何体,根据三棱柱,圆锥,圆柱,四棱柱的特点判断即可.
【详解】解:三棱柱,四棱柱的截面不可能是圆,圆锥,圆柱的截面可能是圆,
故选:C.
10.B
【分析】本题考查简单的几何图形具有的特点,根据立体图形的特征,点、线、面、体,圆锥的特征和截一个几何体的方法判断即可.
【详解】解:①五棱柱有10个顶点,15条棱,7个面,所以①错误,不符合题意.
②点动成线,线动成面,面动成体,所以②正确,符合题意.
③圆锥的侧面展开图是一个扇形,所以③错误,不符合题意.
④用平面去截一个正方体,截面的形状可以是三角形、四边形、五边形、六边形,所以④正确,符合题意.
综上所述,说法正确的有2个,
故选:B.
11.
【分析】∵圆柱侧面积=底面周长×高,∴底面半径=底面周长÷2π=圆柱侧面积÷高÷2π.
【详解】解:根据圆柱的侧面积公式可得这个圆柱的底面半径==2(cm).
故答案为2.
本题主要考查了圆柱的侧面积的计算方法.
12. 6 2 4
【详解】试题分析:首先找出正方体相对的面,然后进行计算.根据题意可得:5+b=1+a=3+c,则a=6,b=2,c=4.
考点:正方体的展开图
13.12
【分析】根据n棱柱的特点,由n个侧面和两个底面构成,可得该棱柱是四棱柱,由此即可解答.
【详解】解:由题意可知:6-2=4,
故该棱柱是四棱柱,它的棱数是12.
故答案为:12.
本题主要考查了棱柱的概念,根据棱柱的底面和侧面的关系求解是解题关键.
14. AA1; A1B1; AC;
【分析】在长方体中,棱与棱之间有平行,相交(垂直)和异面等关系,即可得出结果.
【详解】解:(1)与棱BB1 平行的棱是AA1,
故答案为:AA1;
(2)与棱BB1相交的棱是A1 B1,
故答案为:A1B1;
(3)与棱BB1不在同一平面内的棱是AC,
故答案为:AC.
本题考查了立体图形的有关概念;熟记棱与棱之间有平行,相交(垂直)和异面等关系是解决问题的关键.
15.6
【分析】根据四棱柱有两个底面,四个侧面,即可解答.
【详解】解:∵四棱柱有两个底面,四个侧面,,
∴四棱柱是由6个面围成.
故答案为:6.
16.3/三
【分析】根据圆柱的几何特征求解即可.
【详解】解:∵圆柱有上下两个底面,一个侧面,
∴圆柱有3个面,
故答案为:3.
本题考查圆柱,熟知常见几何体的几何特征是解答的关键.
17. ①②⑥ ⑤
【分析】根据立体图形的特征即可得到答案.
【详解】解:柱体的有①②⑥;球体有⑤.
故答案为:①②⑥,⑤
本题考查了认识立体图形,熟知立体图形的特征并知道他们的名称是解题关键.
18.
【分析】本题考查了运用正方体的相对面解答问题,根据与相邻的面的数字有判断出的对面数字是,与相邻的面的数字有判断出4的对面数字是,从而确定出的对面数字是,然后确定出的值,相加即可求解,正确判断对面和邻面是解题的关键.
【详解】解:由图可知,
∵与相邻的面的数字有,
∴的对面数字是,
∵与相邻的面的数字有,
∴的对面数字是,
∴的对面数字是,
∵标有数字的面所对面上的数字记为,的面所对面上数字记为,
∴,,
∴,
故答案为:.
19.πabcm2
【分析】长方形纸片的面积就是圆柱的侧面积,圆柱侧面积=底面周长×高.
【详解】长方形纸片的面积=π×ab=abπ.
则答案为abπcm2.
本题考查了圆柱的相关知识,解题的关键是熟练的掌握圆柱的侧面积公式与运算.
20.8
【分析】观察图形的特征,每一行的图案一样,即可得到答案.
【详解】观察得知,每一行的图形是一样的,第三行的图案均应该是三个圆圈,与8中的图案一样,
故答案为:8.
认识平面图形,找准图形中的规律是解题关键.
21.(1)①,②;
(2)长方体盒子的体积
【分析】本题考查了简单几何体的展开图,熟练根据简单几何的展开图得出长方体的长宽高是解题的关键.
(1)根据长方形面积公式得出答案即可;
(2)根据长方体公式得出答案即可.
【详解】(1)解:①由题意可知,盒子的高为.
②盒子的边长为,
∴盒子的底面面积为.
(2)解:由题意可知,该长方体的底面积为,
∴长方体的体积为,
把,代入可得,
.
22.(1)见解析;(2)
【分析】(1)由已知条件可知,从正面看有3列,每列小正方形的数目分别为;从左面看有3列,每列小正方形的数目分别为;据此画出图形;
(2)根据几何体三个方向看到的图形可求出几何体的表面积.
【详解】解:(1)如图所示:
;
(2),
答:该几何体的表面积为.
本题考查从不同方向看几何体.以及几何体的表面积,由几何体的从上面看到的形状及小正方形内的数字,可知左面的列数与上面的列数相同,且每列小正方形数目为俯视图中该列小正方形数字中的最大数字.左面的列数与上面的行数相同,且每列小正方形数目为上面看到的图中相应行中正方形数字中的最大数字.
23.(1)①④
(2)
(3),图见解析
【分析】(1)根据三棱柱的特点求解即可;
(2)结合图形利用棱长计算周长即可;
(3)要使得外围的周长最大,使得漏在外面的侧棱最多即可.
【详解】(1)解:根据三棱柱的特点可得①④为展开图,
故答案为:①④;
(2)图3的外围周长为
(3)图形不唯一,例如:
最大周长为:.
本题主要考查三棱柱的展开图及周长的计算,熟练掌握立体图形的展开图特点是解题关键.
24.见详解
【分析】本题考查了从不同方向看几何体;
从正面看有3列,左侧有3个正方形,中间有1个正方形,右侧有1个正方形;从左边看有2列,左侧有3个正方形,右侧有1个正方形;从上面看有3列,左侧有1个正方形,中间有2个正方形,右侧有1个正方形;
【详解】解:如图
25.都能围成棱柱,依次为四棱柱(长方体),五棱柱,三棱柱.
【分析】本题是操作问题,可以尝试操作,或想象操作.根据棱柱的特征,特别是侧面和上下两个底面的位置特征作答.
【详解】第一个图形可以围成直四棱柱;
第二个图折叠后可以围成五棱柱;
第三个图形,将两个长方形往中间的那个面折叠,即可得一三棱柱.可以折成三棱柱.
本题考查了展开图折叠成几何体,熟练掌握常见立体图形的平面展开图的特征,是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
