全等三角形的判定(HL) 专项练习(含解析)
文档属性
| 名称 | 全等三角形的判定(HL) 专项练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-28 13:52:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
全等三角形的判定(HL) 专项练习
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级上·广东中山·期末)如图,于点 C,于点D,要根据“”直接证明 与全等, 则还需要添加一个条件是( )
A. B. C. D.
2.(23-24八年级下·湖南岳阳·期中)如图,于点D,于点F,.证明不是利用“”的条件是( )
A. B. C. D.
3.(2024七年级下·全国·专题练习)在中,,E是上的一点,且,过E作交于D,如果,则等于( )
A. B. C. D.
4.(23-24八年级下·安徽蚌埠·开学考试)如图所示,在中,,,于点,于点,,,则的长是( )
A. B. C. D.
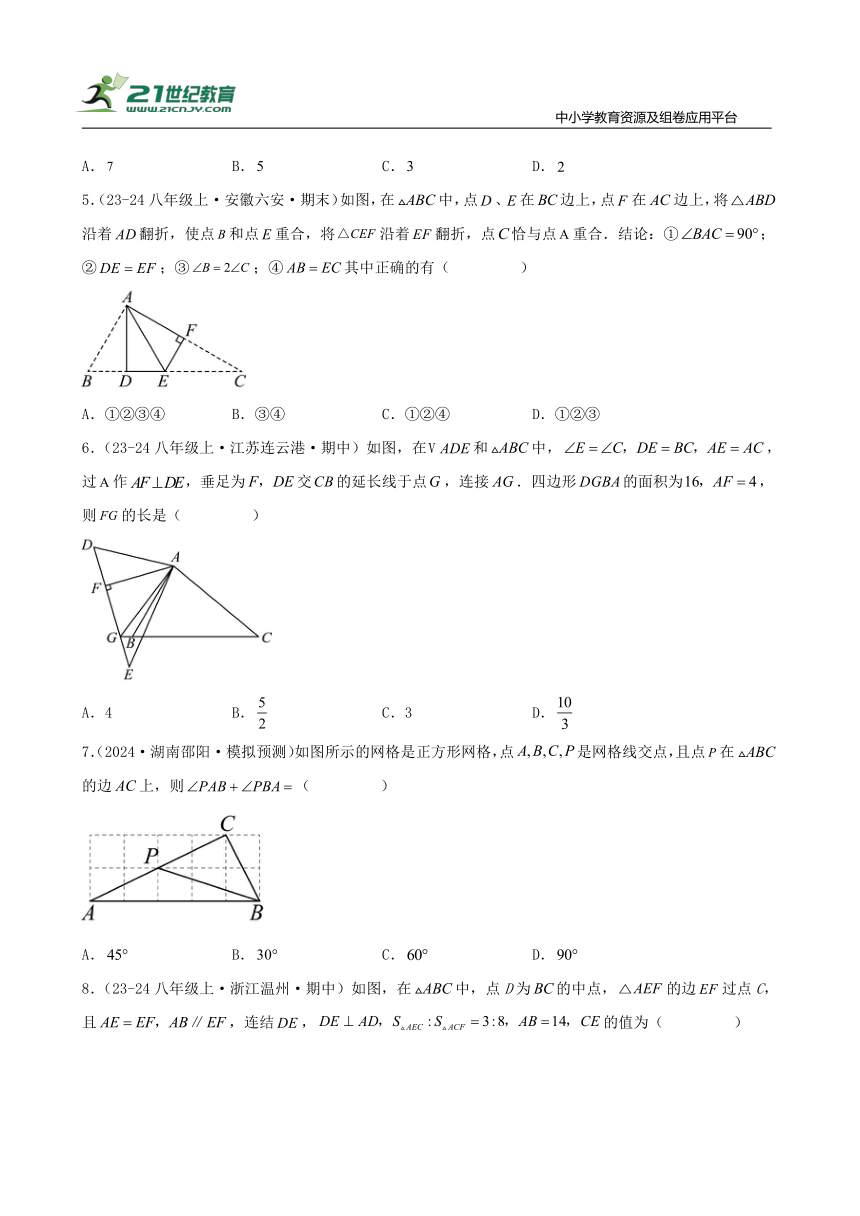
5.(23-24八年级上·安徽六安·期末)如图,在中,点、在边上,点在边上,将沿着翻折,使点和点重合,将沿着翻折,点恰与点重合.结论:①;②;③;④其中正确的有( )
A.①②③④ B.③④ C.①②④ D.①②③
6.(23-24八年级上·江苏连云港·期中)如图,在和中,,过作,垂足为交的延长线于点,连接.四边形的面积为,则的长是( )
A.4 B. C.3 D.
7.(2024·湖南邵阳·模拟预测)如图所示的网格是正方形网格,点是网格线交点,且点在的边上,则( )
A. B. C. D.
8.(23-24八年级上·浙江温州·期中)如图,在中,点D为的中点,的边过点C,且,连结,的值为( )
A. B.4 C. D.3
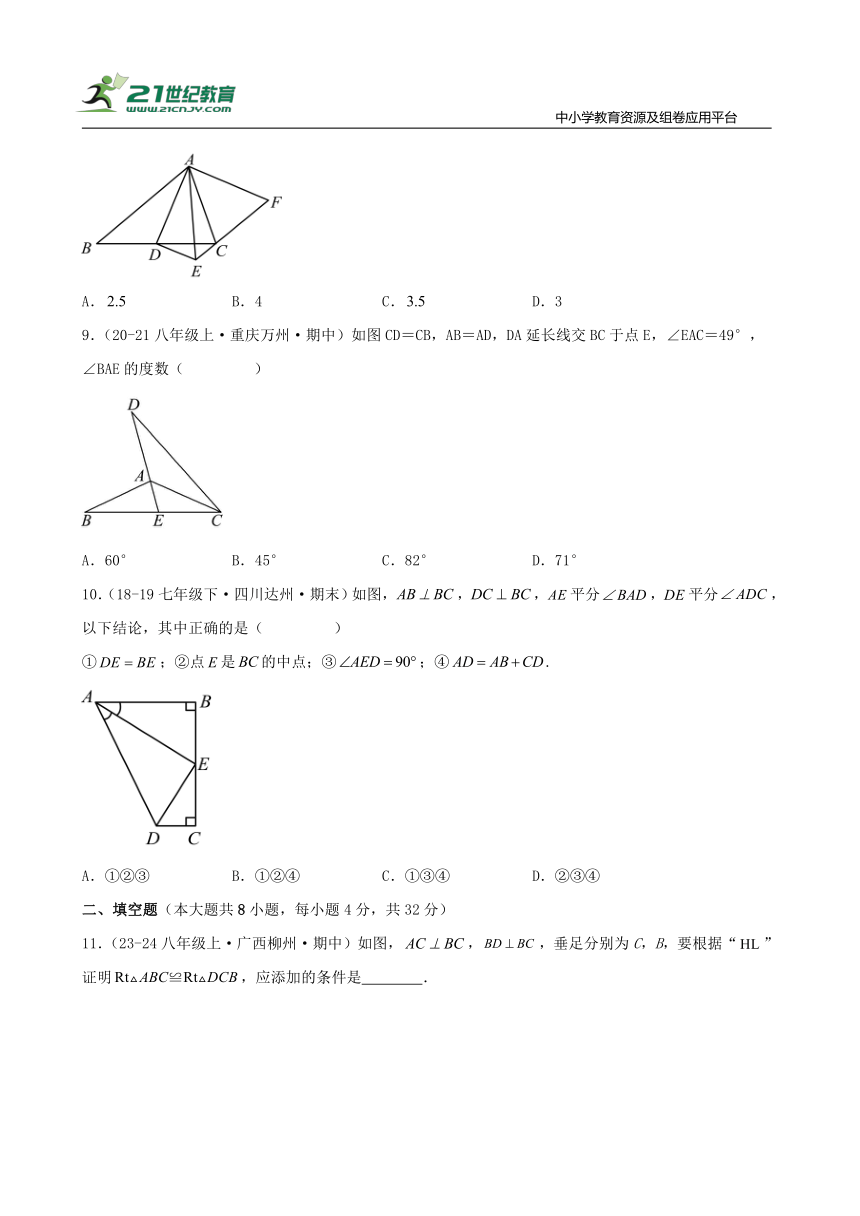
9.(20-21八年级上·重庆万州·期中)如图CD=CB,AB=AD,DA延长线交BC于点E,∠EAC=49°,∠BAE的度数( )
A.60° B.45° C.82° D.71°
10.(18-19七年级下·四川达州·期末)如图,,,平分,平分,以下结论,其中正确的是( )
①;②点是的中点;③;④.
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(本大题共8小题,每小题4分,共32分)
11.(23-24八年级上·广西柳州·期中)如图,,,垂足分别为C,B,要根据“”证明,应添加的条件是 .
12.(23-24八年级下·湖南郴州·阶段练习)如图,点D在上,.若,则 .
13.(23-24八年级上·广东中山·期中)如图,已知平分于点E,于点F,,cm,cm,则的长度为 cm.
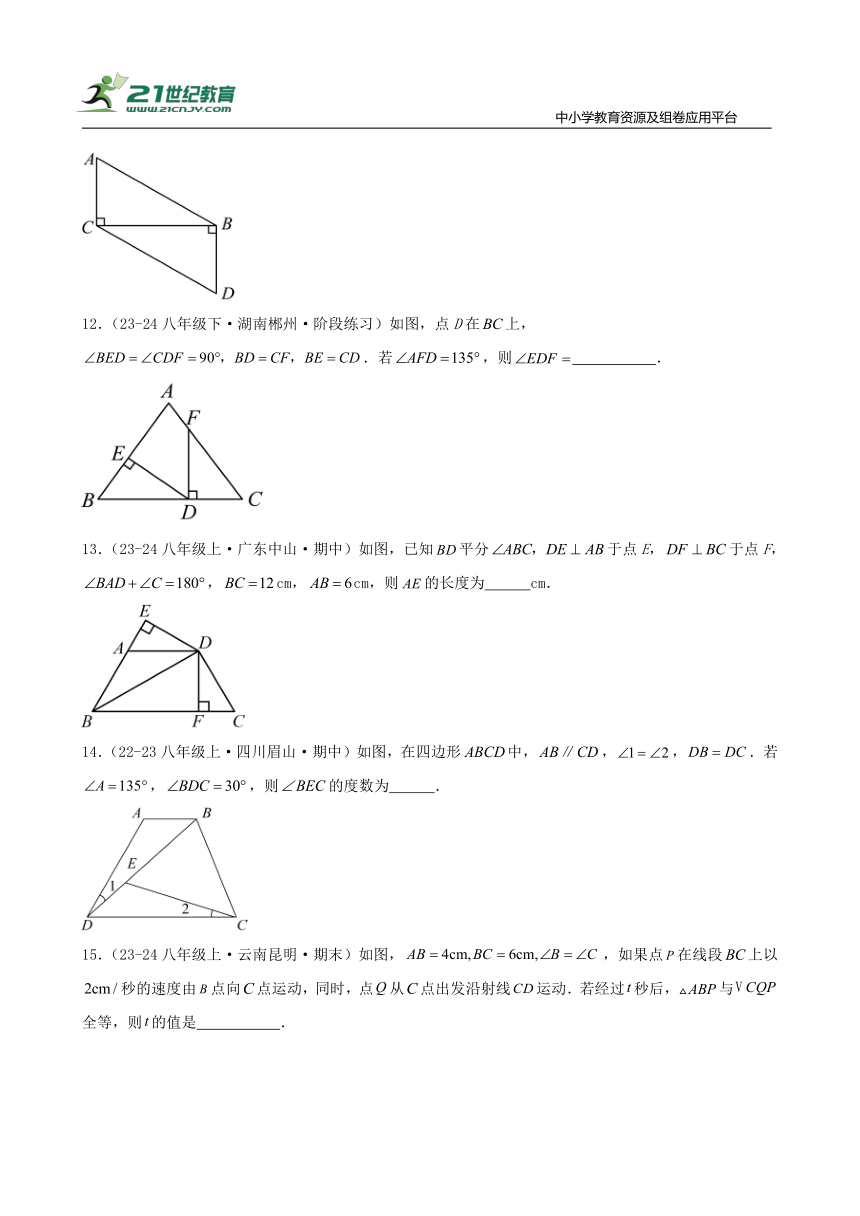
14.(22-23八年级上·四川眉山·期中)如图,在四边形中,,,.若,,则的度数为 .
15.(23-24八年级上·云南昆明·期末)如图,,如果点在线段上以秒的速度由点向点运动,同时,点从点出发沿射线运动.若经过秒后,与全等,则的值是 .
16.(23-24八年级上·安徽合肥·期末)如图,点是内一点,连接、、,其中,平分,若的面积为4,则的面积是 .
17.(23-24八年级上·浙江台州·期中)如图,在中,,是的平分线,于点,点在上,,若,,则的长为 .
18.(23-24八年级上·江苏常州·阶段练习)如图,在和中,,,,过A作,垂足为F,交的延长线于点G,连接.四边形的面积为12,,则的长是 .
三、解答题(本大题共6小题,共58分)
19.(8分)(2023八年级上·全国·专题练习)如图,在四边形中,于,,.
求证:;.
(8分)(22-23八年级上·河北张家口·期末)如图,在中,于点,点在上,,,点为的中点,连接并延长至点,使,连接.
求证:
(1);
(2).
21.(10分)(23-24八年级下·辽宁锦州·期中)已知:如图,在 中,的角平分线与的垂直平分线交于点D, 垂足分别为E,F.
(1)求证:;
(2)若 求 的周长.
22.(10分)(23-24八年级上·广西贵港·期末)小强在物理课上学习了发声物体的振动试验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,A表示小球静止时的位置,当小强用发声物体靠近小球时,小球从A摆到位置,此时过点作于点,当小球摆到位置时,过点作于点,测得(图中的点在同一平面内).
(1)猜想此时与的位置关系,并说明理由;
(2)求的长.
23.(10分)(23-24八年级上·安徽六安·期末)在中,,点分别在边上,
(1)如图(1),若,求证:.
(2)如图(2),若,则线段与线段相等吗?如果相等,请给出证明;如果不相等,请说明理由.
24.(12分)(23-24七年级下·江西吉安·阶段练习)综合与探究
问题背景
数学活动课上,“兴趣小组”将一副三角尺按不同的摆放位置来探究三条线段的数量关系.
特例探究
(1)“兴趣小组”的同学决定从特例人手探究,他们将含的三角尺按如图1所示的方式摆放在直线l上,,直线l经过点A,直线l,直线l,垂足分别为D,E,则之间的数量关系为__________.
类比探究
(2)“兴趣小组”的同学将一副三角尺按如图2所示的方式叠放在一起,当顶点B在线段上且顶点A在线段上时,过点C作,垂足为P,猜想之间的数量关系,并说明理由.
拓展应用
(3)“兴趣小组”的同学将一副三角尺按如图3所示的方式叠放在一起,当顶点A在线段上且顶点B在线段上时,连接,若,求的面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.D
【分析】本题主要考查了添加一个条件使得三角形全等,根据HL定理的条件进行判断即可;
【详解】解:∵,,
∴当时,.
当时,.
故选D.
2.B
【分析】本题主要考查了直角三角形全等的判定,掌握斜边和一条直角边对应相等的两个直角三角形全等是解答本题的关键.根据直角三角形全等的判定方法进行判断即可.
【详解】解:∵于点D,于点F,.
∴,
∵,
∴补充:或,
可得:,故A,C不符合题意;
补充,
∴,
∴,故D不符合题意;
补充,
∴,
∴,故B符合题意;
故选B
3.B
【分析】本题考查了全等三角形的判定及性质,判定三角形全等的方法有、、、、.
根据可判定,再根据全等三角形的性质得出,最后根据线段的和差即可得出答案.
【详解】解:∵,
∴,
在和中,
∴,
∴,
∴,
故选:B.
4.B
【分析】此题主要考查直角三角形的全等判定与性质,首先证明,又由,,得出,,进而得出答案.
【详解】解:∵,,,,
∴,
∴
又∵,,
∴,,
∴.
故选B
5.B
【分析】本题考查翻折变换,等边三角形的判定,全等三角形的判定和性质,三角形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题.将沿着翻折,可得,,将沿着翻折,可得,,进而得到,,从而判断①②正确,再假设③④成立,得到与题干条件矛盾,从而判断①②不一定正确.
【详解】解:∵将沿着翻折,使点B和点E重合,
∴,,
∵将沿着翻折,点C恰与点A重合,
∴,,
∴,∴④正确;
∵,
∴,故③正确;
当,则,
∴,,
∴为等边三角形,与题干条件矛盾,故①不准确,
同理:当,而,,
则,
∴,
结合三角形的内角和可得:,与题干条件矛盾,故②不准确,
故选:B.
6.A
【分析】本题考查了全等三角形的判定与性质以及三角形面积等知识.过点作于,证,得,再证,同理,得,进而得到的长.
【详解】解:过点作于,如图所示:
在和中,
,
∴,
,
又∵,
∴,
∴,
∵,
∴,
在和中,
,
∴,
同理:,
∴,
∵,
,
,
∴,
解得:;
故选:A.
7.A
【分析】根据全等三角形的判定与性质,,再根据直角三角形的判定及性质可知,最后利用三角形外角的性质即可解答.本题考查了全等三角形的判定与性质,直角三角形的判定与性质,三角形的外角的性质,掌握全等三角形的判定与性质是解题的关键,
【详解】解:∵ ,,,
∴,
∴,,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∴,
故选:.
8.D
【分析】本题主要考查了平行线的性质,三角形全等的判定和性质,熟练掌握以上知识点是解题的关键.由可得到,再由,D为的中点,得到和,根据线段比例关系得出结果即可.
【详解】解:延长,交于点,如图所示
,D为的中点,
,
又,
,
,
同理可证:,
,
,
,
∵,
∴.
故选:D.
9.C
【分析】证明△ABC≌△ADC得∠D+∠ACD=∠B+∠ACB=49°,进而根据三角形内角和定理得结果.
【详解】解:∵AC平分∠DCB,
∴∠BCA=∠DCA,
又∵CB=CD,AC=AC,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∴∠B+∠ACB=∠D+∠ACD,
∵∠CAE=∠D+∠ACD=49°,
∴∠B+∠ACB=49°,
∴∠BAE=180°-∠B-∠ACB-∠CAE=82°,
故选:C.
【点拨】本题主要考查了角平分线的定义,全等三角形的性质与判定,三角形的内角和定理,三角形的外角定理,关键是证明三角形全等,求得∠B+∠ACB=49°.
10.D
【分析】如图作EH⊥AD于H.利用角平分线的性质定理,证明三角形全等即可解决问题;
【详解】解:如图作EH⊥AD于H.
∵平分,,EH⊥AD,
∴EH=BE,
∵DE>EH,
∴DE>BE,故①错误,
∵EA平分∠BAD,EB⊥BA,EH⊥AD,
∴BE=EH,
同法可证:EH=EC,
∴EB=EC,故②正确,
∵∠B=∠EHA=90°,AE=AE,EB=EH,
∴Rt△EAB≌Rt△EAH(HL),
∴AH=AB,∠AEB=∠AEH,
同理可证:△EDH≌△EDC(HL),
∴DH=DC,∠DEH=∠DEC,
∴AD=AH+DH=AB+CD,∠AED=(∠BEH+∠CEH)=90°,故③④正确,
故选D.
【点拨】本题考查全等三角形的判定和性质、角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
11.
【分析】根据“”判定方法求解即可.此题考查了全等三角形的判定,熟记全等三角形的判定方法“”是解题的关键.
【详解】解:应添加的条件是,理由是:
∵,,
∴,
∵,,
∴,
即应添加的条件是,
故答案为:.
12./45度
【分析】本题考查了全等三角形的判定与性质.证明,可得,即可求解.
【详解】解:∵,
∴.
又∵,
在与中,
∵,
∴,
∴,
∴.
故答案为:
13.3
【分析】本题考查了角平分线的性质以及全等三角形的判定与性质,证、是解题关键.
【详解】解:∵平分于点E,于点F,
∴
∵
∴
∴
∵,
∴
∵
∴
∴
∵,cm,cm,
∴
故答案为:3
14./度
【分析】证可得,即可求解.
【详解】解:∵
∴
∵,
∴
∴
∴
故答案为:.
【点拨】本题考查了全等三角形的判定与性质.熟记相关内容是解题关键.
15.1或
【分析】本题主要考查了全等三角形的性质,利用全等三角形对应边相等,列出方程是解题的关键.利用分类讨论的思想方法分两种情况讨论解答:①当和②当时,设运动时间为秒,点的运动速度为秒,利用全等三角形对应边相等,列出方程即可求解.
【详解】解:设.两点的运动时间为秒,点的运动速度为秒,
则,,.
,
①当时,
,.
,
;
②当时,
,,
,
.
综上,当的值是1或时,能够使与全等.
故答案为:1或.
16.8
【分析】本题考查了三角形全等的判定及性质,三角形的面积公式,角平分的性质,证明 可得到,是解题关键.
【详解】解:延长交于点E如图:
,平分,
,
,
,
,,
,
的面积为4,
,
故答案为:8.
17.
【分析】此题考查了全等三角形的判定与性质,以及角平分线性质;由为角平分线,利用角平分线定理得到,再由,利用得到三角形与三角形全等,利用全等三角形对应边相等得出,利用得到三角形与三角形全等,利用全等三角形对应边相等得到,由,即可求解.
【详解】解:是的平分线,,,
,
在和中,
,
,
,
;
在和中,
,
,
,
,
故答案:.
18.3
【分析】过点作于,证,得,再证,同理,得6,进而得到的长.
【详解】解:过点作于,如图所示:
在和中,
,
∴
又∵,
∴,
∴,
∵,
∴,
在和中,
∴,
同理:,
∴,
∵,
∴,
解得:;
故答案为:3.
【点拨】本题考查了全等三角形的判定与性质以及三角形面积等知识,解决问题的关键是作辅助线构造全等三角形,解题时注意:全等三角形的面积相等.
19.详见解析
【分析】过点向作垂线,构建全等三角形,继而根据平角定义以及线段的和差即可证得结论.
【详解】如图,过点作与点,则,
,,
,
,,
,,
,
,,
∵,
,
.
【点拨】本题考查了全等三角形的判定与性质,正确添加辅助线构建全等三角形是解题的关键.
20.(1)见解析
(2)见解析
【分析】(1))先根据垂直的定义可得和都是直角三角形,再利用定理证明三角形全等即可;
(2)根据证明,得到再利用直角三角形的两锐角互余得出.
【详解】(1),
.
又,,
;
(2)为中点,
.
,,
,
.
由(1)得,
.
,
,
.
【点拨】本题考查了直角三角形全等的判定定理与性质、直角三角形的性质等知识点,熟练掌握三角形全等的判定方法是解题关键.
21.(1)详见解析
(2)17
【分析】此题考查了全等三角形的判定和性质、垂直平分线的性质等知识,熟练掌握全等三角形的判定和性质是解题的关键.
(1)证明,即可得到结论;
(2)证明,则,由(1)可知,即可得到答案.
【详解】(1)证明:连接.
∵D在的中垂线上
∴
∵.平分
∴
∴
∴
(2)∵平分
∴
∵
∴
又∵.
∴
∴
由 (1) 可知
∴的周长为:
22.(1);见解析
(2)
【分析】本题主要考查了三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定和性质.
(1)证明,得出,根据,求出,即可证明结论;
(2)根据,得出,根据,求出结果即可.
【详解】(1)解:,理由如下:
∵于D,于E,
∴,
又∵根据题意得:,,
∴,
∴,
又∵,
∴,
即,
∴;
(2)解:∵,
∴,
又∵,
∴,
答:的长为.
23.(1)证明详见解析;
(2)相等,理由详见解析.
【分析】本题考查了直角三角形的全等判定和性质,三角形全等的判定和性质.
(1)根据直角三角形的全等判定证明即可.
(2)过点作交的延长线于,过点作交的延长线于.仿照(1)证明直角三角形全等即可.
【详解】(1),
均为直角三角形,
又
.
(2)相等,理由如下:
如图所示,过点作交的延长线于,过点作交的延长线于.
,
,
,
,
,
.
24.(1);(2),理由见解析;(3)
【分析】本题考查了全等三角形的判定与性质,三角板中角度的计算,线段的和差计算,熟练掌握相关性质定理是解题关键
(1)根据题意可知两个三角板都是等腰直角三角形,可证,从而得出三边关系;
(2)通过角度之间的关系得出,从而证明,从而得出三边关系;
(3)先证明,得出,从而求出结果.
【详解】解:(1),理由如下:
由题意可知:,,,
所以,
所以,
所以.
(2).
理由:因为,
所以.
因为,
所以,
所以,
所以.
因为,
所以,
所以.
因为,
所以.
(3)如图,过点C作交的延长线于点P.
因为,
所以.
因为,
所以,
所以,
所以.
全等三角形的判定(HL) 专项练习
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级上·广东中山·期末)如图,于点 C,于点D,要根据“”直接证明 与全等, 则还需要添加一个条件是( )
A. B. C. D.
2.(23-24八年级下·湖南岳阳·期中)如图,于点D,于点F,.证明不是利用“”的条件是( )
A. B. C. D.
3.(2024七年级下·全国·专题练习)在中,,E是上的一点,且,过E作交于D,如果,则等于( )
A. B. C. D.
4.(23-24八年级下·安徽蚌埠·开学考试)如图所示,在中,,,于点,于点,,,则的长是( )
A. B. C. D.
5.(23-24八年级上·安徽六安·期末)如图,在中,点、在边上,点在边上,将沿着翻折,使点和点重合,将沿着翻折,点恰与点重合.结论:①;②;③;④其中正确的有( )
A.①②③④ B.③④ C.①②④ D.①②③
6.(23-24八年级上·江苏连云港·期中)如图,在和中,,过作,垂足为交的延长线于点,连接.四边形的面积为,则的长是( )
A.4 B. C.3 D.
7.(2024·湖南邵阳·模拟预测)如图所示的网格是正方形网格,点是网格线交点,且点在的边上,则( )
A. B. C. D.
8.(23-24八年级上·浙江温州·期中)如图,在中,点D为的中点,的边过点C,且,连结,的值为( )
A. B.4 C. D.3
9.(20-21八年级上·重庆万州·期中)如图CD=CB,AB=AD,DA延长线交BC于点E,∠EAC=49°,∠BAE的度数( )
A.60° B.45° C.82° D.71°
10.(18-19七年级下·四川达州·期末)如图,,,平分,平分,以下结论,其中正确的是( )
①;②点是的中点;③;④.
A.①②③ B.①②④ C.①③④ D.②③④
二、填空题(本大题共8小题,每小题4分,共32分)
11.(23-24八年级上·广西柳州·期中)如图,,,垂足分别为C,B,要根据“”证明,应添加的条件是 .
12.(23-24八年级下·湖南郴州·阶段练习)如图,点D在上,.若,则 .
13.(23-24八年级上·广东中山·期中)如图,已知平分于点E,于点F,,cm,cm,则的长度为 cm.
14.(22-23八年级上·四川眉山·期中)如图,在四边形中,,,.若,,则的度数为 .
15.(23-24八年级上·云南昆明·期末)如图,,如果点在线段上以秒的速度由点向点运动,同时,点从点出发沿射线运动.若经过秒后,与全等,则的值是 .
16.(23-24八年级上·安徽合肥·期末)如图,点是内一点,连接、、,其中,平分,若的面积为4,则的面积是 .
17.(23-24八年级上·浙江台州·期中)如图,在中,,是的平分线,于点,点在上,,若,,则的长为 .
18.(23-24八年级上·江苏常州·阶段练习)如图,在和中,,,,过A作,垂足为F,交的延长线于点G,连接.四边形的面积为12,,则的长是 .
三、解答题(本大题共6小题,共58分)
19.(8分)(2023八年级上·全国·专题练习)如图,在四边形中,于,,.
求证:;.
(8分)(22-23八年级上·河北张家口·期末)如图,在中,于点,点在上,,,点为的中点,连接并延长至点,使,连接.
求证:
(1);
(2).
21.(10分)(23-24八年级下·辽宁锦州·期中)已知:如图,在 中,的角平分线与的垂直平分线交于点D, 垂足分别为E,F.
(1)求证:;
(2)若 求 的周长.
22.(10分)(23-24八年级上·广西贵港·期末)小强在物理课上学习了发声物体的振动试验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,A表示小球静止时的位置,当小强用发声物体靠近小球时,小球从A摆到位置,此时过点作于点,当小球摆到位置时,过点作于点,测得(图中的点在同一平面内).
(1)猜想此时与的位置关系,并说明理由;
(2)求的长.
23.(10分)(23-24八年级上·安徽六安·期末)在中,,点分别在边上,
(1)如图(1),若,求证:.
(2)如图(2),若,则线段与线段相等吗?如果相等,请给出证明;如果不相等,请说明理由.
24.(12分)(23-24七年级下·江西吉安·阶段练习)综合与探究
问题背景
数学活动课上,“兴趣小组”将一副三角尺按不同的摆放位置来探究三条线段的数量关系.
特例探究
(1)“兴趣小组”的同学决定从特例人手探究,他们将含的三角尺按如图1所示的方式摆放在直线l上,,直线l经过点A,直线l,直线l,垂足分别为D,E,则之间的数量关系为__________.
类比探究
(2)“兴趣小组”的同学将一副三角尺按如图2所示的方式叠放在一起,当顶点B在线段上且顶点A在线段上时,过点C作,垂足为P,猜想之间的数量关系,并说明理由.
拓展应用
(3)“兴趣小组”的同学将一副三角尺按如图3所示的方式叠放在一起,当顶点A在线段上且顶点B在线段上时,连接,若,求的面积.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.D
【分析】本题主要考查了添加一个条件使得三角形全等,根据HL定理的条件进行判断即可;
【详解】解:∵,,
∴当时,.
当时,.
故选D.
2.B
【分析】本题主要考查了直角三角形全等的判定,掌握斜边和一条直角边对应相等的两个直角三角形全等是解答本题的关键.根据直角三角形全等的判定方法进行判断即可.
【详解】解:∵于点D,于点F,.
∴,
∵,
∴补充:或,
可得:,故A,C不符合题意;
补充,
∴,
∴,故D不符合题意;
补充,
∴,
∴,故B符合题意;
故选B
3.B
【分析】本题考查了全等三角形的判定及性质,判定三角形全等的方法有、、、、.
根据可判定,再根据全等三角形的性质得出,最后根据线段的和差即可得出答案.
【详解】解:∵,
∴,
在和中,
∴,
∴,
∴,
故选:B.
4.B
【分析】此题主要考查直角三角形的全等判定与性质,首先证明,又由,,得出,,进而得出答案.
【详解】解:∵,,,,
∴,
∴
又∵,,
∴,,
∴.
故选B
5.B
【分析】本题考查翻折变换,等边三角形的判定,全等三角形的判定和性质,三角形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题.将沿着翻折,可得,,将沿着翻折,可得,,进而得到,,从而判断①②正确,再假设③④成立,得到与题干条件矛盾,从而判断①②不一定正确.
【详解】解:∵将沿着翻折,使点B和点E重合,
∴,,
∵将沿着翻折,点C恰与点A重合,
∴,,
∴,∴④正确;
∵,
∴,故③正确;
当,则,
∴,,
∴为等边三角形,与题干条件矛盾,故①不准确,
同理:当,而,,
则,
∴,
结合三角形的内角和可得:,与题干条件矛盾,故②不准确,
故选:B.
6.A
【分析】本题考查了全等三角形的判定与性质以及三角形面积等知识.过点作于,证,得,再证,同理,得,进而得到的长.
【详解】解:过点作于,如图所示:
在和中,
,
∴,
,
又∵,
∴,
∴,
∵,
∴,
在和中,
,
∴,
同理:,
∴,
∵,
,
,
∴,
解得:;
故选:A.
7.A
【分析】根据全等三角形的判定与性质,,再根据直角三角形的判定及性质可知,最后利用三角形外角的性质即可解答.本题考查了全等三角形的判定与性质,直角三角形的判定与性质,三角形的外角的性质,掌握全等三角形的判定与性质是解题的关键,
【详解】解:∵ ,,,
∴,
∴,,
∵,
∴,
∴,
∴是等腰直角三角形,
∴,
∴,
故选:.
8.D
【分析】本题主要考查了平行线的性质,三角形全等的判定和性质,熟练掌握以上知识点是解题的关键.由可得到,再由,D为的中点,得到和,根据线段比例关系得出结果即可.
【详解】解:延长,交于点,如图所示
,D为的中点,
,
又,
,
,
同理可证:,
,
,
,
∵,
∴.
故选:D.
9.C
【分析】证明△ABC≌△ADC得∠D+∠ACD=∠B+∠ACB=49°,进而根据三角形内角和定理得结果.
【详解】解:∵AC平分∠DCB,
∴∠BCA=∠DCA,
又∵CB=CD,AC=AC,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∴∠B+∠ACB=∠D+∠ACD,
∵∠CAE=∠D+∠ACD=49°,
∴∠B+∠ACB=49°,
∴∠BAE=180°-∠B-∠ACB-∠CAE=82°,
故选:C.
【点拨】本题主要考查了角平分线的定义,全等三角形的性质与判定,三角形的内角和定理,三角形的外角定理,关键是证明三角形全等,求得∠B+∠ACB=49°.
10.D
【分析】如图作EH⊥AD于H.利用角平分线的性质定理,证明三角形全等即可解决问题;
【详解】解:如图作EH⊥AD于H.
∵平分,,EH⊥AD,
∴EH=BE,
∵DE>EH,
∴DE>BE,故①错误,
∵EA平分∠BAD,EB⊥BA,EH⊥AD,
∴BE=EH,
同法可证:EH=EC,
∴EB=EC,故②正确,
∵∠B=∠EHA=90°,AE=AE,EB=EH,
∴Rt△EAB≌Rt△EAH(HL),
∴AH=AB,∠AEB=∠AEH,
同理可证:△EDH≌△EDC(HL),
∴DH=DC,∠DEH=∠DEC,
∴AD=AH+DH=AB+CD,∠AED=(∠BEH+∠CEH)=90°,故③④正确,
故选D.
【点拨】本题考查全等三角形的判定和性质、角平分线的性质定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
11.
【分析】根据“”判定方法求解即可.此题考查了全等三角形的判定,熟记全等三角形的判定方法“”是解题的关键.
【详解】解:应添加的条件是,理由是:
∵,,
∴,
∵,,
∴,
即应添加的条件是,
故答案为:.
12./45度
【分析】本题考查了全等三角形的判定与性质.证明,可得,即可求解.
【详解】解:∵,
∴.
又∵,
在与中,
∵,
∴,
∴,
∴.
故答案为:
13.3
【分析】本题考查了角平分线的性质以及全等三角形的判定与性质,证、是解题关键.
【详解】解:∵平分于点E,于点F,
∴
∵
∴
∴
∵,
∴
∵
∴
∴
∵,cm,cm,
∴
故答案为:3
14./度
【分析】证可得,即可求解.
【详解】解:∵
∴
∵,
∴
∴
∴
故答案为:.
【点拨】本题考查了全等三角形的判定与性质.熟记相关内容是解题关键.
15.1或
【分析】本题主要考查了全等三角形的性质,利用全等三角形对应边相等,列出方程是解题的关键.利用分类讨论的思想方法分两种情况讨论解答:①当和②当时,设运动时间为秒,点的运动速度为秒,利用全等三角形对应边相等,列出方程即可求解.
【详解】解:设.两点的运动时间为秒,点的运动速度为秒,
则,,.
,
①当时,
,.
,
;
②当时,
,,
,
.
综上,当的值是1或时,能够使与全等.
故答案为:1或.
16.8
【分析】本题考查了三角形全等的判定及性质,三角形的面积公式,角平分的性质,证明 可得到,是解题关键.
【详解】解:延长交于点E如图:
,平分,
,
,
,
,,
,
的面积为4,
,
故答案为:8.
17.
【分析】此题考查了全等三角形的判定与性质,以及角平分线性质;由为角平分线,利用角平分线定理得到,再由,利用得到三角形与三角形全等,利用全等三角形对应边相等得出,利用得到三角形与三角形全等,利用全等三角形对应边相等得到,由,即可求解.
【详解】解:是的平分线,,,
,
在和中,
,
,
,
;
在和中,
,
,
,
,
故答案:.
18.3
【分析】过点作于,证,得,再证,同理,得6,进而得到的长.
【详解】解:过点作于,如图所示:
在和中,
,
∴
又∵,
∴,
∴,
∵,
∴,
在和中,
∴,
同理:,
∴,
∵,
∴,
解得:;
故答案为:3.
【点拨】本题考查了全等三角形的判定与性质以及三角形面积等知识,解决问题的关键是作辅助线构造全等三角形,解题时注意:全等三角形的面积相等.
19.详见解析
【分析】过点向作垂线,构建全等三角形,继而根据平角定义以及线段的和差即可证得结论.
【详解】如图,过点作与点,则,
,,
,
,,
,,
,
,,
∵,
,
.
【点拨】本题考查了全等三角形的判定与性质,正确添加辅助线构建全等三角形是解题的关键.
20.(1)见解析
(2)见解析
【分析】(1))先根据垂直的定义可得和都是直角三角形,再利用定理证明三角形全等即可;
(2)根据证明,得到再利用直角三角形的两锐角互余得出.
【详解】(1),
.
又,,
;
(2)为中点,
.
,,
,
.
由(1)得,
.
,
,
.
【点拨】本题考查了直角三角形全等的判定定理与性质、直角三角形的性质等知识点,熟练掌握三角形全等的判定方法是解题关键.
21.(1)详见解析
(2)17
【分析】此题考查了全等三角形的判定和性质、垂直平分线的性质等知识,熟练掌握全等三角形的判定和性质是解题的关键.
(1)证明,即可得到结论;
(2)证明,则,由(1)可知,即可得到答案.
【详解】(1)证明:连接.
∵D在的中垂线上
∴
∵.平分
∴
∴
∴
(2)∵平分
∴
∵
∴
又∵.
∴
∴
由 (1) 可知
∴的周长为:
22.(1);见解析
(2)
【分析】本题主要考查了三角形全等的判定和性质,解题的关键是熟练掌握三角形全等的判定和性质.
(1)证明,得出,根据,求出,即可证明结论;
(2)根据,得出,根据,求出结果即可.
【详解】(1)解:,理由如下:
∵于D,于E,
∴,
又∵根据题意得:,,
∴,
∴,
又∵,
∴,
即,
∴;
(2)解:∵,
∴,
又∵,
∴,
答:的长为.
23.(1)证明详见解析;
(2)相等,理由详见解析.
【分析】本题考查了直角三角形的全等判定和性质,三角形全等的判定和性质.
(1)根据直角三角形的全等判定证明即可.
(2)过点作交的延长线于,过点作交的延长线于.仿照(1)证明直角三角形全等即可.
【详解】(1),
均为直角三角形,
又
.
(2)相等,理由如下:
如图所示,过点作交的延长线于,过点作交的延长线于.
,
,
,
,
,
.
24.(1);(2),理由见解析;(3)
【分析】本题考查了全等三角形的判定与性质,三角板中角度的计算,线段的和差计算,熟练掌握相关性质定理是解题关键
(1)根据题意可知两个三角板都是等腰直角三角形,可证,从而得出三边关系;
(2)通过角度之间的关系得出,从而证明,从而得出三边关系;
(3)先证明,得出,从而求出结果.
【详解】解:(1),理由如下:
由题意可知:,,,
所以,
所以,
所以.
(2).
理由:因为,
所以.
因为,
所以,
所以,
所以.
因为,
所以,
所以.
因为,
所以.
(3)如图,过点C作交的延长线于点P.
因为,
所以.
因为,
所以,
所以,
所以.
