探索三角形全等的条件(HL) 专项练习(含解析)
文档属性
| 名称 | 探索三角形全等的条件(HL) 专项练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-28 13:53:57 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
探索三角形全等的条件(HL) 专项练习
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级下·山西晋中·期中)如图,已知,,若用“”判定和全等,则需要添加的条件是( )
A. B. C. D.
2.(23-24八年级上·湖北随州·期末)如图,于P,,添加下列一个条件,能利用“”判定的条件是( )
A. B.与互余 C. D.
3.(23-24八年级上·河南南阳·阶段练习)如图,在和中,,,,则下列结论不一定成立的是()
A. B. C. D.
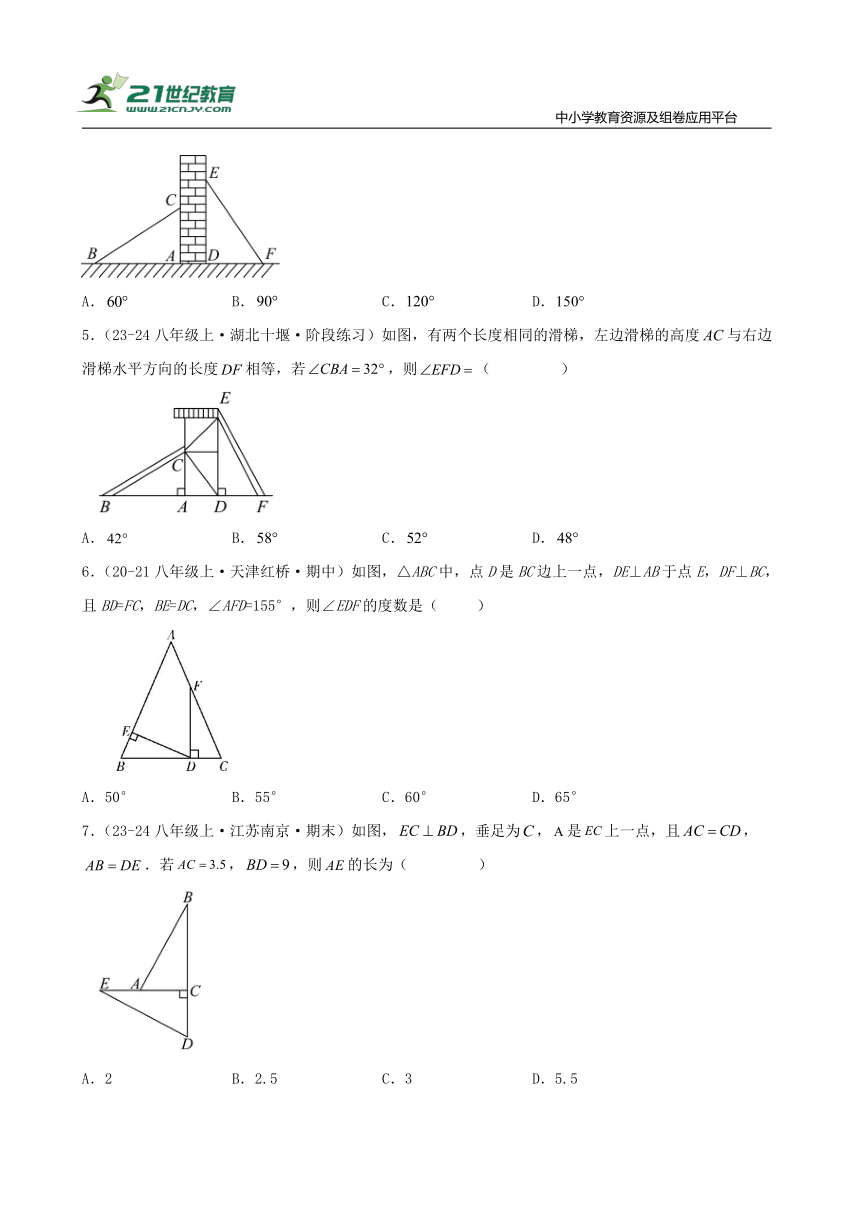
4.(22-23八年级上·江西抚州·期中)如图,有两个长度相同的滑梯靠在一面墙上.已知,则这两个滑梯与地面夹角与的度数和是( )
A. B. C. D.
5.(23-24八年级上·湖北十堰·阶段练习)如图,有两个长度相同的滑梯,左边滑梯的高度与右边滑梯水平方向的长度相等,若,则( )
A. B. C. D.
6.(20-21八年级上·天津红桥·期中)如图,△ABC中,点D是BC边上一点,DE⊥AB于点E,DF⊥BC,且BD=FC,BE=DC,∠AFD=155°,则∠EDF的度数是( )
A.50° B.55° C.60° D.65°
7.(23-24八年级上·江苏南京·期末)如图,,垂足为,是上一点,且,.若,,则的长为( )
A.2 B.2.5 C.3 D.5.5
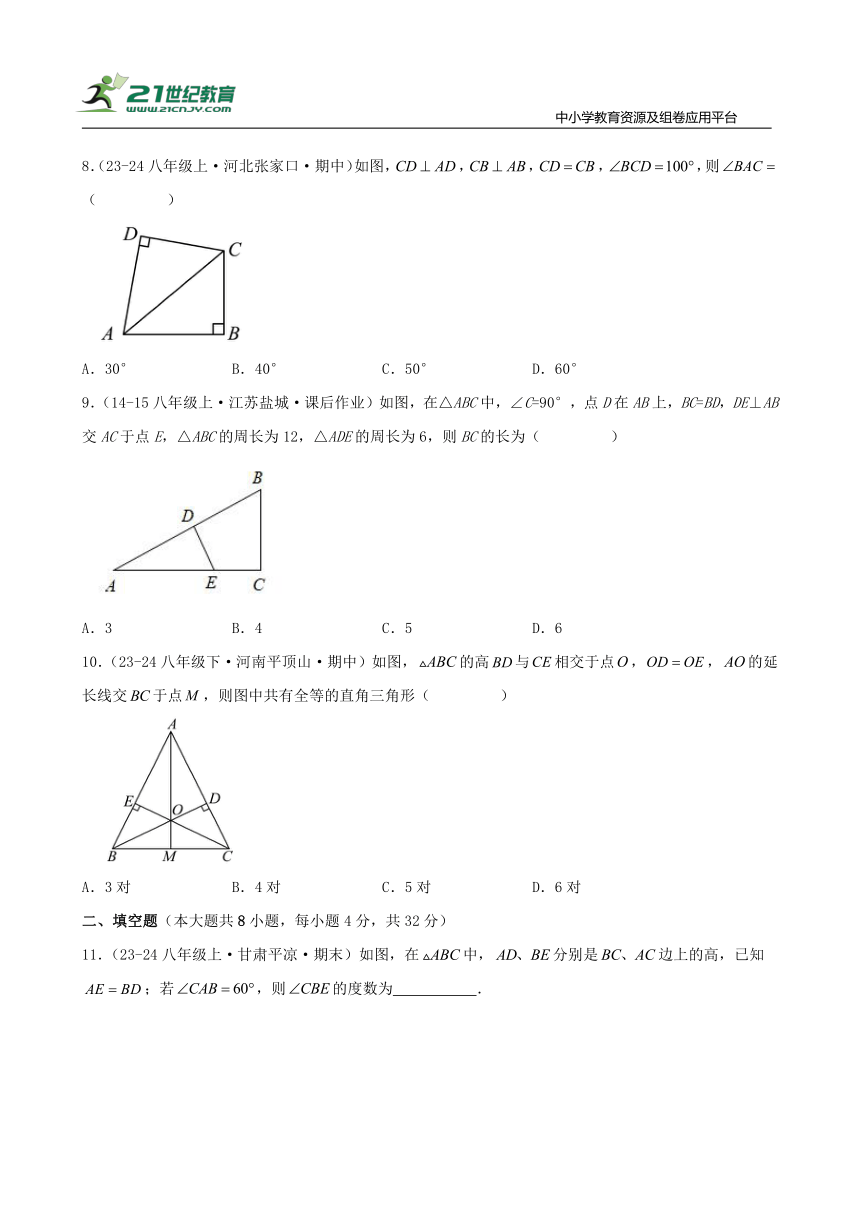
8.(23-24八年级上·河北张家口·期中)如图,,,,,则( )
A.30° B.40° C.50° D.60°
9.(14-15八年级上·江苏盐城·课后作业)如图,在△ABC中,∠C=90°,点D在AB上,BC=BD,DE⊥AB交AC于点E,△ABC的周长为12,△ADE的周长为6,则BC的长为( )
A.3 B.4 C.5 D.6
10.(23-24八年级下·河南平顶山·期中)如图,的高与相交于点,,的延长线交于点,则图中共有全等的直角三角形( )
A.3对 B.4对 C.5对 D.6对
二、填空题(本大题共8小题,每小题4分,共32分)
11.(23-24八年级上·甘肃平凉·期末)如图,在中,分别是边上的高,已知;若,则的度数为 .
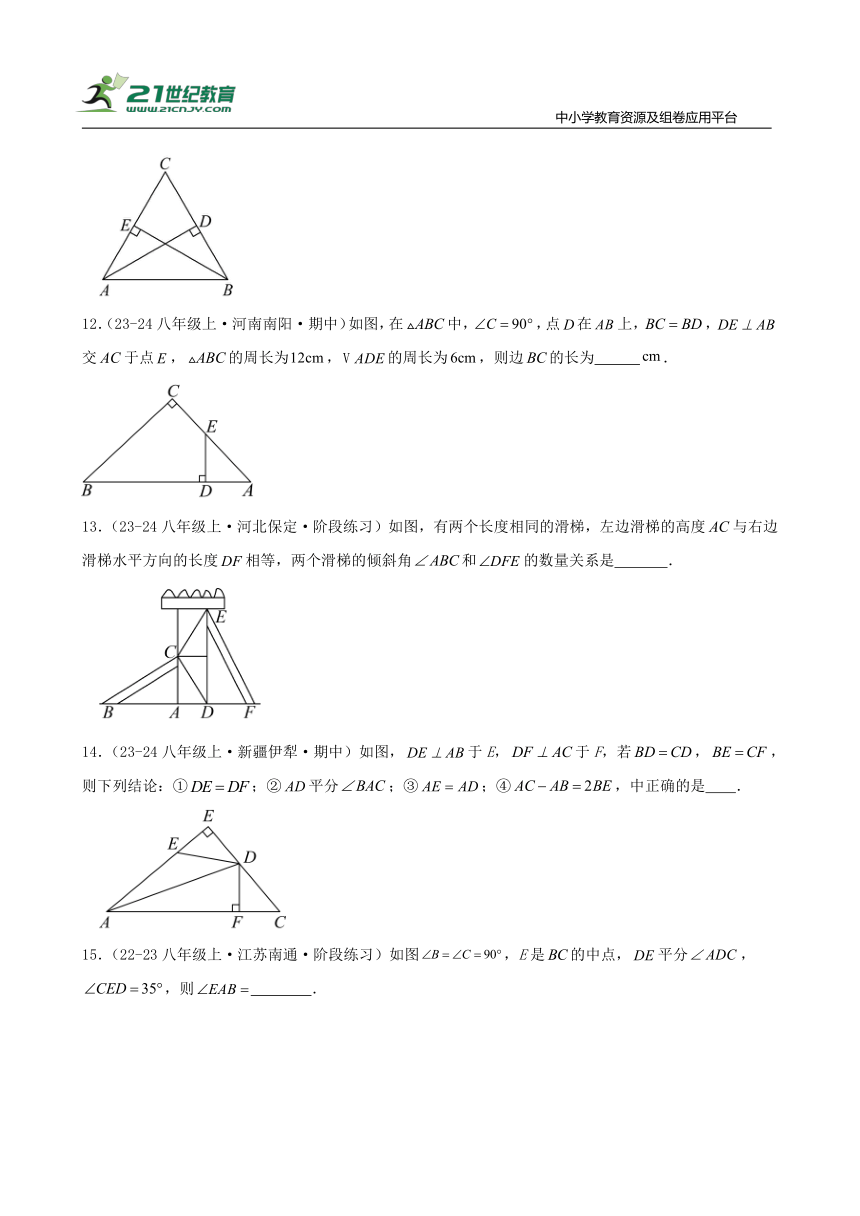
12.(23-24八年级上·河南南阳·期中)如图,在中,,点在上,,交于点,的周长为,的周长为,则边的长为 .
13.(23-24八年级上·河北保定·阶段练习)如图,有两个长度相同的滑梯,左边滑梯的高度与右边滑梯水平方向的长度相等,两个滑梯的倾斜角和的数量关系是 .
14.(23-24八年级上·新疆伊犁·期中)如图,于E,于F,若,,则下列结论:①;②平分;③;④,中正确的是 .
15.(22-23八年级上·江苏南通·阶段练习)如图,E是的中点,平分,,则 .
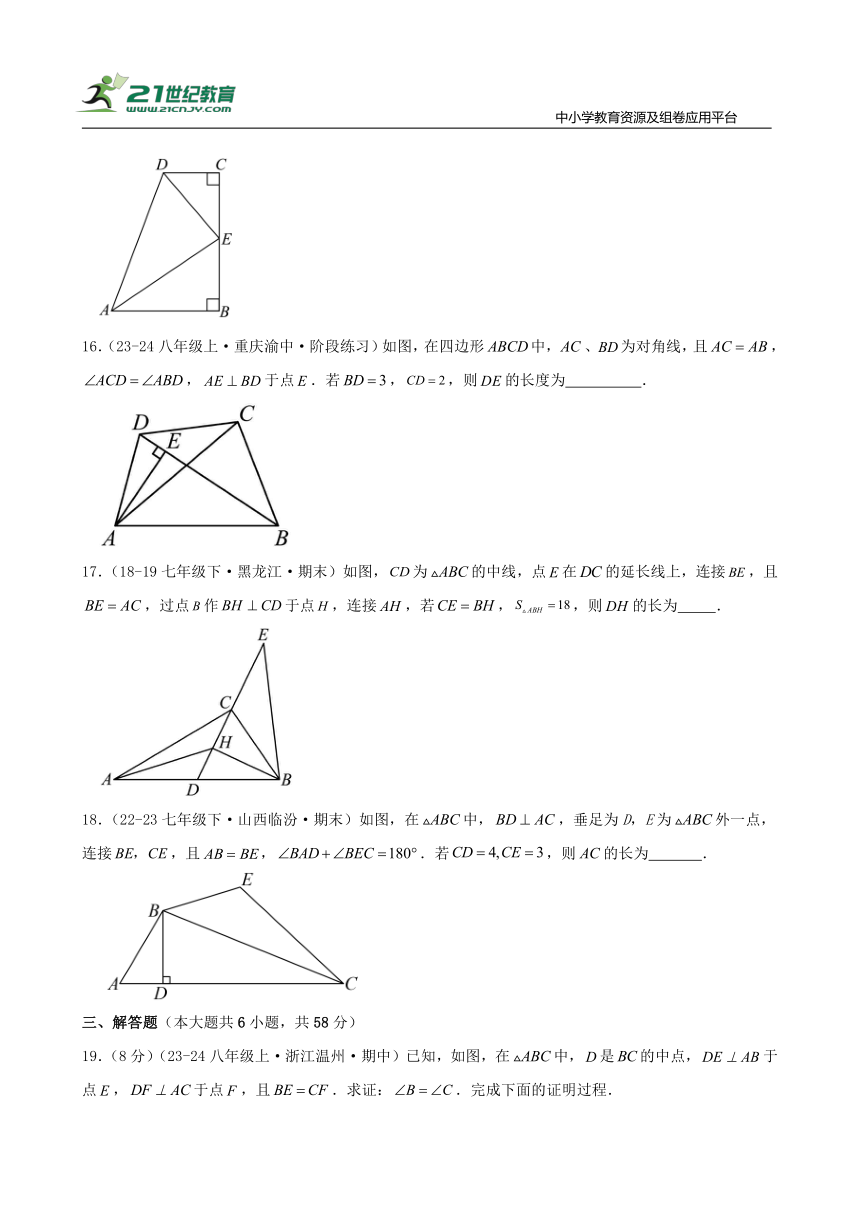
16.(23-24八年级上·重庆渝中·阶段练习)如图,在四边形中,、为对角线,且,,于点.若,,则的长度为 .
17.(18-19七年级下·黑龙江·期末)如图,为的中线,点在的延长线上,连接,且,过点作于点,连接,若,,则的长为 .
18.(22-23七年级下·山西临汾·期末)如图,在中,,垂足为D,E为外一点,连接,且,.若,则的长为 .
三、解答题(本大题共6小题,共58分)
19.(8分)(23-24八年级上·浙江温州·期中)已知,如图,在中,是的中点,于点,于点,且.求证:.完成下面的证明过程.
证明:
,,
__________.
是的中点,
__________,
又,
__________.
.
20.(8分)(23-24八年级上·内蒙古巴彦淖尔·阶段练习)如图,相交于点O,,.
(1)求证:;
(2)若,求的度数.
21.(10分)(23-24八年级下·陕西咸阳·阶段练习)如图,已知,,点在边的延长线上,连接,的平分线交于点,过点作,垂足为,且.
(1)求的度数;
(2)请判断是否平分,并说明理由.
22.(10分)(23-24八年级上·河北邢台·阶段练习)如图,在中,,在的上方作,使,且,与交于点,连接.
(1)若平分,求证:.
(2)求的度数.
23.(10分)(21-22八年级上·山东聊城·期末)如图,在△ABC中∠ABC=45°,AD⊥BC于点D,点E为AD上的一点,且BE=AC,延长BE交AC于点F,连接FD.
(1)求证:△BED≌△ACD;
(2)若FC=c,FB=b,求的值.(用含a,b的式子表示)
24.(12分)(20-21七年级下·辽宁朝阳·期末)已知:两个等腰直角三角板△ACB和△DCE(AC=BC,DC=CE,∠ACB=∠DCE=90°)如图所示摆放,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.
(1)如图1(两个等腰直角三角板大小不等),试判断AE与BD有何关系并说明理由;
(2)如图2(两个等腰直角三角板大小相等,即AC=DC),在不添加任何辅助线的情况,请直接写出图2中四对全等的直角三角形.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查了直角三角形全等的判定定理的应用,根据垂直定义得出,根据图形可知是公共直角边,根据直角三角形全等的判定得出需要添加的条件是斜边相等,能熟记全等三角形的判定定理是解题的关键.
【详解】解:∵,,
∴,
在和中,
,
∴,
故选:.
2.D
【分析】本题考查了全等三角形的判定与性质,熟练掌握“”是解答本题的关键.根据“”所需的条件分析即可.
【详解】解:∵,
∴,
∵,
∴要利用“”判定的条件是.
故选D.
3.B
【分析】本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形的判定和性质,属于基础题.
首先证明,推出,,由,推出,推出,即可一一判断.
【详解】解:在和中,
,
故A、C、D正确,
故选:B.
4.B
【分析】本题主要考查了全等三角形的性质与判定,三角形内角和定理,利用证明得到,由可得.
【详解】解:由题意得,,
∵,
∴,
∴,
∵,
∴,即.
故选:B.
5.B
【分析】先根据证明,再根据全等三角形的性质得出,最后根据直角三角形两锐角互余即可求解.
【详解】解:在和中,
,
∴,
∴,
∴,
故选:B.
【点拨】本题主要考查了用证明三角形全等,解题的关键掌握有一条直角和斜边相等的两个直角三角形全等.
6.D
【分析】证明Rt△FDC≌Rt△DEB(HL),由全等三角形的性质得出∠DFC=∠EDB=25°,即可得出答案.
【详解】解:∵∠AFD=155°,
∴∠DFC=25°,
∵DF⊥BC,DE⊥AB,
∴∠FDC=∠DEB=90°,
在Rt△FDC和Rt△DEB中,,
∴Rt△FDC≌Rt△DEB(HL),
∴∠DFC=∠EDB=25°,
∴∠EDF=180° ∠BDE ∠FDC=180° 25° 90°=65°.
故选:D.
【点拨】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理和性质定理是解题的关键.
7.A
【分析】本题考查全等三角形的判定与性质,根据题意,利用直角三角形全等的判定定理得到,求出相关线段长度,由图中线段关系表示出,代值求解即可得到答案,熟练掌握两个三角形全等的判定与性质是解决问题的关键.
【详解】解:,
,
,
,
在和中,
,
,
,
,
故选:A.
8.B
【分析】本题主要考查全等三角形的判定与性质,直角三角形中两个锐角互余,根据条件证明出两个直角三角形全等是解题的关键.
【详解】解:,,
,
在和中,
,
,
,
,
,
.
故选:B.
9.A
【分析】先根据角平分线的性质得到ED=EC,再证明Rt△BED≌Rt△BEC得到DE=CE,接着利用三角形周长和等线段代换得到AD+AC+2BC=12和AD+AC=6,所以6+2BC=12,从而得到BC的长.
【详解】解:连接BE,
∵DE⊥AB
∴∠BDE=90°,
在Rt△BED和Rt△BEC中,
,
∴Rt△BED≌Rt△BEC(HL),
∴DE=CE,
∵△ABC的周长为12,
∴AB+AC+BC=12,
即AD+AC+2BC=12,
∵△ADE的周长为6,
∴AD+DE+AE=6,
即AD+EC+AE=6,
∴AD+AC=6,
∴6+2BC=12,
∴BC=3.
故选:A.
【点拨】本题考查了全等三角形的判定和性质,掌握HL证明全等是解答此题的关键.
10.D
【分析】本题主要考查了直角三角形全等的判定方法,判定两个直角三角形全等的一般方法有:.熟练掌握运用全等三角形的判定方法是解题关键.
,,利用全等三角形的判定可证明,做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【详解】解:,.理由如下:
在与中,,
,
∴,
∴,
在与中,
∴,
∴,
∴,即,
∵,
∴.
在与中,,
,
∴.
在与中,,
,
∴.
在与中,
,
∴.
在与中,,
∴.
故选:D
11./度
【分析】本题考查了全等三角形的判定与性质,证即可求解.
【详解】解:∵分别是边上的高,
∴
∵,
∴
∵,
∴
∴,
∴
故答案为:
12.3
【分析】本题主要考查了全等三角形的性质与判定,如图所示,连接,利用证明得到,根据三角形周长公式推出,再由,可得.
【详解】解:如图所示,连接,
∵,,
∴,
在和中,
,
∴,
∴,
∵的周长为,的周长为,
∴,
∴,即,
∵,
∴,
∴,
故答案为:3.
13.
【分析】由条件信息可得,与均是直角三角形,由已知可根据判定两三角形全等,再根据全等三角形的对应角相等,不难求解.
【详解】解:,证明如下:
由题意可得:与均是直角三角形,且.
在和中,
,
∴,
∴,
∵,
∴.
故答案为:
【点拨】此题考查了全等三角形的应用.做题时要注意找已知条件,根据已知选择方法得出全等三角形是解题关键.
14.①②④
【分析】本题考查了全等三角形的判定与性质.利用证明全等,根据全等三角形对应边相等可得,再证明,判断出平分,可得,再根据图形即可得到.
【详解】解:∵,
∴,
又∵,,
∴,
∴,①正确,符合题意;
又∵,,
∴,
∴,,即平分,②正确,符合题意;
∴,④正确,符合题意;
在中,,∴,③错误,不符合题意;
综上所述,正确的是①②④.
故答案为:①②④.
15.
【分析】过点E作,垂足为F.由三角形的内角和定理求得,由角平分线的定义可知,由平行线的判定定理可知,由平行线的性质可求得,由角平分线的性质可知,则,根据可证明,从而得到.
【详解】解:过点E作,垂足为F.
∵,
∴.
∵平分,
∴.
∴.
∵,
∴.
∴.
∴.
∵平分,,
∴.
∵E是的中点,
∴.
在和中,
,
∴.
∴.
∴.
故选答案为.
【点拨】本题主要考查的是角平分线的性质、全等三角形的性质和判定、平行线的性质和判定、三角形的内角和定理等知识点,由角平分线的性质证得是解题的关键.
16.
【分析】过点A作交的延长线于点F,根据证明,得到,,再根据证明,得到,最后根据线段的和差即可求解.
【详解】解:过点A作交的延长线于点F,
,
,
,
在和中,
,
,
∴,,
在和中,
,
,
,
,,,
,
,
,,
,
,
故答案为:.
【点拨】此题主要考查了全等三角形的判定与性质,正确作出辅助线构造全等三角形是解答此题的关键.
17.
【分析】
过点作于点,证明,,得出,再由为的中线及,根据的面积列出关于的方程,求解即可.
【详解】
解:如图,过点作于点
为的中线,
,
又
,
在和中
,即
,,
为的中线,
又
解得:
故答案为:3.
【点拨】
本题考查了全等三角形的判定与性质、等底同高三角形的面积关系及直角三角形的面积公式,属于中档题.
18.5
【分析】如图,过作的延长线于,证明,则,,证明,则,,,根据,计算求解即可.
【详解】解:如图,过作的延长线于,
∵,,
∴,
∵,,,
∴,
∴,,
∵,,
∴,
∴,
∴,,
∴,
故答案为:5.
【点拨】本题考查了全等三角形的判定与性质.解题的关键在于明确线段之间的数量关系.
19.,,
【分析】本题考查了全等三角形的判定与性质知识;证明,得出即可.证明三角形全等是解题的关键.
【详解】解:,,
是的中点,
又,
.
20.(1)见详解
(2)
【分析】(1)由“”可证;
(2)由全等三角形的性质可得,即可求解.
【详解】(1)证明:∵,
∴和都是直角三角形,
在和中,
,
∴;
(2)在中,
∵,
由(1)可知,
【点拨】本题考查了全等三角形的判定和性质,证明是本题的关键.
21.(1)
(2)平分,理由见解析
【分析】(1)由平角的定义可求解的度数,再利用三角形的内角和定理可求解,进而可求解;(2)过点分别作于点,于点,根据角平分线的性质可证得,进而可证明结论.
【详解】(1),
.
,
.
,
,
;
(2)平分
理由:如图,过点分别作于点,于点
平分
在和中
(AAS)
同理可得:
在和中,
(HL)
平分.
【点拨】本题主要考查角平分线的判定与性质,三角形的内角和定理,掌握角平分线的判定与性质是解题的关键.
22.(1)见解析
(2)
【分析】本题主要考查全等三角形的判定和性质即角平分线性质,
(1)延长,交于点,由题意得,有,由垂直得,证得,有即可证明结论;
(2)过点分别作于点,于点,有,得到,可得,即可求得角度.
【详解】(1)证明:延长,交于点,如图,
,,,
,
,
.
,,
.
,,
,
,
.
(2)解:过点分别作于点,于点,如图,
.
,,
,
,
∵,
∴,
.
23.(1)见解析
(2)
【分析】(1)利用得,又BE=AC,,因此可以通过HL定理证明;
(2)作于点,作于点,由可得,利用即可求解.
【详解】(1)证明:在△ABC中∠ABC=45°,AD⊥BC,
,,
,
在和中,
,
,
即.
(2)解:如图所示,作DG⊥BE于点G,作DH⊥AC于点H,
由(1)知
,
,
,
,
.
【点拨】本题考查全等三角形的判定和性质,以及三角形的面积公式,解题的关键是正确作出辅助线,由可得.
24.(1)AE=BD且AE⊥BD.理由见解析;(2)△ACB≌△DCE,△EMC≌△BCN,△AON≌△DOM,△AOB≌△DOE
【分析】(1)证明△ACE≌△BCD,可得AE=BD,∠CEA=∠BDC,由∠CME=∠DMO,根据三角形内角和定理即可得∠DOM=∠ECM=90°,进而可证AE⊥BD.
(2)根据三角形全等的判定找出相等边和角,进而找出全等三角形.
【详解】解:(1)结论;AE=BD且AE⊥BD.理由如下:
∵∠ACB=∠DCE,
∴∠ACB+∠DCA=∠DCE+∠DCA,
即∠DCB=∠ACE,
∵AC=BC,CD=CE,
在△ACE与△BCD中,
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CEA=∠BDC,
∵∠CME=∠DMO,
,
即∠DOM=∠ECM=90°,
∴AE⊥BD,
∴AE=BD且AE⊥BD;
(2)∵AC=DC,
∴AC=CD=EC=CB,
在△ACB与△DCE中,
,
∴△ACB≌△DCE(SAS);
由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC,
∴∠DOM=90°,
∵∠AEC=∠CAE=∠CBD,
∴△EMC≌△BCN(ASA),
∴CM=CN,
∴DM=AN,
∴△AON≌△DOM(AAS),
∵DE=AB,AO=DO,
∴△AOB≌△DOE(HL).
【点拨】本题考查了三角形全等的性质与判定,掌握三角形全等的性质与判定是解题的关键.
探索三角形全等的条件(HL) 专项练习
一、单选题(本大题共10小题,每小题3分,共30分)
1.(23-24八年级下·山西晋中·期中)如图,已知,,若用“”判定和全等,则需要添加的条件是( )
A. B. C. D.
2.(23-24八年级上·湖北随州·期末)如图,于P,,添加下列一个条件,能利用“”判定的条件是( )
A. B.与互余 C. D.
3.(23-24八年级上·河南南阳·阶段练习)如图,在和中,,,,则下列结论不一定成立的是()
A. B. C. D.
4.(22-23八年级上·江西抚州·期中)如图,有两个长度相同的滑梯靠在一面墙上.已知,则这两个滑梯与地面夹角与的度数和是( )
A. B. C. D.
5.(23-24八年级上·湖北十堰·阶段练习)如图,有两个长度相同的滑梯,左边滑梯的高度与右边滑梯水平方向的长度相等,若,则( )
A. B. C. D.
6.(20-21八年级上·天津红桥·期中)如图,△ABC中,点D是BC边上一点,DE⊥AB于点E,DF⊥BC,且BD=FC,BE=DC,∠AFD=155°,则∠EDF的度数是( )
A.50° B.55° C.60° D.65°
7.(23-24八年级上·江苏南京·期末)如图,,垂足为,是上一点,且,.若,,则的长为( )
A.2 B.2.5 C.3 D.5.5
8.(23-24八年级上·河北张家口·期中)如图,,,,,则( )
A.30° B.40° C.50° D.60°
9.(14-15八年级上·江苏盐城·课后作业)如图,在△ABC中,∠C=90°,点D在AB上,BC=BD,DE⊥AB交AC于点E,△ABC的周长为12,△ADE的周长为6,则BC的长为( )
A.3 B.4 C.5 D.6
10.(23-24八年级下·河南平顶山·期中)如图,的高与相交于点,,的延长线交于点,则图中共有全等的直角三角形( )
A.3对 B.4对 C.5对 D.6对
二、填空题(本大题共8小题,每小题4分,共32分)
11.(23-24八年级上·甘肃平凉·期末)如图,在中,分别是边上的高,已知;若,则的度数为 .
12.(23-24八年级上·河南南阳·期中)如图,在中,,点在上,,交于点,的周长为,的周长为,则边的长为 .
13.(23-24八年级上·河北保定·阶段练习)如图,有两个长度相同的滑梯,左边滑梯的高度与右边滑梯水平方向的长度相等,两个滑梯的倾斜角和的数量关系是 .
14.(23-24八年级上·新疆伊犁·期中)如图,于E,于F,若,,则下列结论:①;②平分;③;④,中正确的是 .
15.(22-23八年级上·江苏南通·阶段练习)如图,E是的中点,平分,,则 .
16.(23-24八年级上·重庆渝中·阶段练习)如图,在四边形中,、为对角线,且,,于点.若,,则的长度为 .
17.(18-19七年级下·黑龙江·期末)如图,为的中线,点在的延长线上,连接,且,过点作于点,连接,若,,则的长为 .
18.(22-23七年级下·山西临汾·期末)如图,在中,,垂足为D,E为外一点,连接,且,.若,则的长为 .
三、解答题(本大题共6小题,共58分)
19.(8分)(23-24八年级上·浙江温州·期中)已知,如图,在中,是的中点,于点,于点,且.求证:.完成下面的证明过程.
证明:
,,
__________.
是的中点,
__________,
又,
__________.
.
20.(8分)(23-24八年级上·内蒙古巴彦淖尔·阶段练习)如图,相交于点O,,.
(1)求证:;
(2)若,求的度数.
21.(10分)(23-24八年级下·陕西咸阳·阶段练习)如图,已知,,点在边的延长线上,连接,的平分线交于点,过点作,垂足为,且.
(1)求的度数;
(2)请判断是否平分,并说明理由.
22.(10分)(23-24八年级上·河北邢台·阶段练习)如图,在中,,在的上方作,使,且,与交于点,连接.
(1)若平分,求证:.
(2)求的度数.
23.(10分)(21-22八年级上·山东聊城·期末)如图,在△ABC中∠ABC=45°,AD⊥BC于点D,点E为AD上的一点,且BE=AC,延长BE交AC于点F,连接FD.
(1)求证:△BED≌△ACD;
(2)若FC=c,FB=b,求的值.(用含a,b的式子表示)
24.(12分)(20-21七年级下·辽宁朝阳·期末)已知:两个等腰直角三角板△ACB和△DCE(AC=BC,DC=CE,∠ACB=∠DCE=90°)如图所示摆放,连接AE、BD交于点O.AE与DC交于点M,BD与AC交于点N.
(1)如图1(两个等腰直角三角板大小不等),试判断AE与BD有何关系并说明理由;
(2)如图2(两个等腰直角三角板大小相等,即AC=DC),在不添加任何辅助线的情况,请直接写出图2中四对全等的直角三角形.
中小学教育资源及组卷应用平台
试卷第1页,共3页
参考答案:
1.D
【分析】本题考查了直角三角形全等的判定定理的应用,根据垂直定义得出,根据图形可知是公共直角边,根据直角三角形全等的判定得出需要添加的条件是斜边相等,能熟记全等三角形的判定定理是解题的关键.
【详解】解:∵,,
∴,
在和中,
,
∴,
故选:.
2.D
【分析】本题考查了全等三角形的判定与性质,熟练掌握“”是解答本题的关键.根据“”所需的条件分析即可.
【详解】解:∵,
∴,
∵,
∴要利用“”判定的条件是.
故选D.
3.B
【分析】本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形的判定和性质,属于基础题.
首先证明,推出,,由,推出,推出,即可一一判断.
【详解】解:在和中,
,
故A、C、D正确,
故选:B.
4.B
【分析】本题主要考查了全等三角形的性质与判定,三角形内角和定理,利用证明得到,由可得.
【详解】解:由题意得,,
∵,
∴,
∴,
∵,
∴,即.
故选:B.
5.B
【分析】先根据证明,再根据全等三角形的性质得出,最后根据直角三角形两锐角互余即可求解.
【详解】解:在和中,
,
∴,
∴,
∴,
故选:B.
【点拨】本题主要考查了用证明三角形全等,解题的关键掌握有一条直角和斜边相等的两个直角三角形全等.
6.D
【分析】证明Rt△FDC≌Rt△DEB(HL),由全等三角形的性质得出∠DFC=∠EDB=25°,即可得出答案.
【详解】解:∵∠AFD=155°,
∴∠DFC=25°,
∵DF⊥BC,DE⊥AB,
∴∠FDC=∠DEB=90°,
在Rt△FDC和Rt△DEB中,,
∴Rt△FDC≌Rt△DEB(HL),
∴∠DFC=∠EDB=25°,
∴∠EDF=180° ∠BDE ∠FDC=180° 25° 90°=65°.
故选:D.
【点拨】本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定定理和性质定理是解题的关键.
7.A
【分析】本题考查全等三角形的判定与性质,根据题意,利用直角三角形全等的判定定理得到,求出相关线段长度,由图中线段关系表示出,代值求解即可得到答案,熟练掌握两个三角形全等的判定与性质是解决问题的关键.
【详解】解:,
,
,
,
在和中,
,
,
,
,
故选:A.
8.B
【分析】本题主要考查全等三角形的判定与性质,直角三角形中两个锐角互余,根据条件证明出两个直角三角形全等是解题的关键.
【详解】解:,,
,
在和中,
,
,
,
,
,
.
故选:B.
9.A
【分析】先根据角平分线的性质得到ED=EC,再证明Rt△BED≌Rt△BEC得到DE=CE,接着利用三角形周长和等线段代换得到AD+AC+2BC=12和AD+AC=6,所以6+2BC=12,从而得到BC的长.
【详解】解:连接BE,
∵DE⊥AB
∴∠BDE=90°,
在Rt△BED和Rt△BEC中,
,
∴Rt△BED≌Rt△BEC(HL),
∴DE=CE,
∵△ABC的周长为12,
∴AB+AC+BC=12,
即AD+AC+2BC=12,
∵△ADE的周长为6,
∴AD+DE+AE=6,
即AD+EC+AE=6,
∴AD+AC=6,
∴6+2BC=12,
∴BC=3.
故选:A.
【点拨】本题考查了全等三角形的判定和性质,掌握HL证明全等是解答此题的关键.
10.D
【分析】本题主要考查了直角三角形全等的判定方法,判定两个直角三角形全等的一般方法有:.熟练掌握运用全等三角形的判定方法是解题关键.
,,利用全等三角形的判定可证明,做题时,要结合已知条件与三角形全等的判定方法逐个验证.
【详解】解:,.理由如下:
在与中,,
,
∴,
∴,
在与中,
∴,
∴,
∴,即,
∵,
∴.
在与中,,
,
∴.
在与中,,
,
∴.
在与中,
,
∴.
在与中,,
∴.
故选:D
11./度
【分析】本题考查了全等三角形的判定与性质,证即可求解.
【详解】解:∵分别是边上的高,
∴
∵,
∴
∵,
∴
∴,
∴
故答案为:
12.3
【分析】本题主要考查了全等三角形的性质与判定,如图所示,连接,利用证明得到,根据三角形周长公式推出,再由,可得.
【详解】解:如图所示,连接,
∵,,
∴,
在和中,
,
∴,
∴,
∵的周长为,的周长为,
∴,
∴,即,
∵,
∴,
∴,
故答案为:3.
13.
【分析】由条件信息可得,与均是直角三角形,由已知可根据判定两三角形全等,再根据全等三角形的对应角相等,不难求解.
【详解】解:,证明如下:
由题意可得:与均是直角三角形,且.
在和中,
,
∴,
∴,
∵,
∴.
故答案为:
【点拨】此题考查了全等三角形的应用.做题时要注意找已知条件,根据已知选择方法得出全等三角形是解题关键.
14.①②④
【分析】本题考查了全等三角形的判定与性质.利用证明全等,根据全等三角形对应边相等可得,再证明,判断出平分,可得,再根据图形即可得到.
【详解】解:∵,
∴,
又∵,,
∴,
∴,①正确,符合题意;
又∵,,
∴,
∴,,即平分,②正确,符合题意;
∴,④正确,符合题意;
在中,,∴,③错误,不符合题意;
综上所述,正确的是①②④.
故答案为:①②④.
15.
【分析】过点E作,垂足为F.由三角形的内角和定理求得,由角平分线的定义可知,由平行线的判定定理可知,由平行线的性质可求得,由角平分线的性质可知,则,根据可证明,从而得到.
【详解】解:过点E作,垂足为F.
∵,
∴.
∵平分,
∴.
∴.
∵,
∴.
∴.
∴.
∵平分,,
∴.
∵E是的中点,
∴.
在和中,
,
∴.
∴.
∴.
故选答案为.
【点拨】本题主要考查的是角平分线的性质、全等三角形的性质和判定、平行线的性质和判定、三角形的内角和定理等知识点,由角平分线的性质证得是解题的关键.
16.
【分析】过点A作交的延长线于点F,根据证明,得到,,再根据证明,得到,最后根据线段的和差即可求解.
【详解】解:过点A作交的延长线于点F,
,
,
,
在和中,
,
,
∴,,
在和中,
,
,
,
,,,
,
,
,,
,
,
故答案为:.
【点拨】此题主要考查了全等三角形的判定与性质,正确作出辅助线构造全等三角形是解答此题的关键.
17.
【分析】
过点作于点,证明,,得出,再由为的中线及,根据的面积列出关于的方程,求解即可.
【详解】
解:如图,过点作于点
为的中线,
,
又
,
在和中
,即
,,
为的中线,
又
解得:
故答案为:3.
【点拨】
本题考查了全等三角形的判定与性质、等底同高三角形的面积关系及直角三角形的面积公式,属于中档题.
18.5
【分析】如图,过作的延长线于,证明,则,,证明,则,,,根据,计算求解即可.
【详解】解:如图,过作的延长线于,
∵,,
∴,
∵,,,
∴,
∴,,
∵,,
∴,
∴,
∴,,
∴,
故答案为:5.
【点拨】本题考查了全等三角形的判定与性质.解题的关键在于明确线段之间的数量关系.
19.,,
【分析】本题考查了全等三角形的判定与性质知识;证明,得出即可.证明三角形全等是解题的关键.
【详解】解:,,
是的中点,
又,
.
20.(1)见详解
(2)
【分析】(1)由“”可证;
(2)由全等三角形的性质可得,即可求解.
【详解】(1)证明:∵,
∴和都是直角三角形,
在和中,
,
∴;
(2)在中,
∵,
由(1)可知,
【点拨】本题考查了全等三角形的判定和性质,证明是本题的关键.
21.(1)
(2)平分,理由见解析
【分析】(1)由平角的定义可求解的度数,再利用三角形的内角和定理可求解,进而可求解;(2)过点分别作于点,于点,根据角平分线的性质可证得,进而可证明结论.
【详解】(1),
.
,
.
,
,
;
(2)平分
理由:如图,过点分别作于点,于点
平分
在和中
(AAS)
同理可得:
在和中,
(HL)
平分.
【点拨】本题主要考查角平分线的判定与性质,三角形的内角和定理,掌握角平分线的判定与性质是解题的关键.
22.(1)见解析
(2)
【分析】本题主要考查全等三角形的判定和性质即角平分线性质,
(1)延长,交于点,由题意得,有,由垂直得,证得,有即可证明结论;
(2)过点分别作于点,于点,有,得到,可得,即可求得角度.
【详解】(1)证明:延长,交于点,如图,
,,,
,
,
.
,,
.
,,
,
,
.
(2)解:过点分别作于点,于点,如图,
.
,,
,
,
∵,
∴,
.
23.(1)见解析
(2)
【分析】(1)利用得,又BE=AC,,因此可以通过HL定理证明;
(2)作于点,作于点,由可得,利用即可求解.
【详解】(1)证明:在△ABC中∠ABC=45°,AD⊥BC,
,,
,
在和中,
,
,
即.
(2)解:如图所示,作DG⊥BE于点G,作DH⊥AC于点H,
由(1)知
,
,
,
,
.
【点拨】本题考查全等三角形的判定和性质,以及三角形的面积公式,解题的关键是正确作出辅助线,由可得.
24.(1)AE=BD且AE⊥BD.理由见解析;(2)△ACB≌△DCE,△EMC≌△BCN,△AON≌△DOM,△AOB≌△DOE
【分析】(1)证明△ACE≌△BCD,可得AE=BD,∠CEA=∠BDC,由∠CME=∠DMO,根据三角形内角和定理即可得∠DOM=∠ECM=90°,进而可证AE⊥BD.
(2)根据三角形全等的判定找出相等边和角,进而找出全等三角形.
【详解】解:(1)结论;AE=BD且AE⊥BD.理由如下:
∵∠ACB=∠DCE,
∴∠ACB+∠DCA=∠DCE+∠DCA,
即∠DCB=∠ACE,
∵AC=BC,CD=CE,
在△ACE与△BCD中,
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CEA=∠BDC,
∵∠CME=∠DMO,
,
即∠DOM=∠ECM=90°,
∴AE⊥BD,
∴AE=BD且AE⊥BD;
(2)∵AC=DC,
∴AC=CD=EC=CB,
在△ACB与△DCE中,
,
∴△ACB≌△DCE(SAS);
由(1)可知:∠AEC=∠BDC,∠EAC=∠DBC,
∴∠DOM=90°,
∵∠AEC=∠CAE=∠CBD,
∴△EMC≌△BCN(ASA),
∴CM=CN,
∴DM=AN,
∴△AON≌△DOM(AAS),
∵DE=AB,AO=DO,
∴△AOB≌△DOE(HL).
【点拨】本题考查了三角形全等的性质与判定,掌握三角形全等的性质与判定是解题的关键.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
