长春市第八中学2023-2024学年高二下学期第一次月考数学试卷(含答案)
文档属性
| 名称 | 长春市第八中学2023-2024学年高二下学期第一次月考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 731.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-27 06:07:03 | ||
图片预览




文档简介
长春市第八中学2023-2024学年高二下学期第一次月考数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知等差数列的公差为4,且,,成等比数列,则( )
A.46 B.48 C.50 D.52
2.下列式子求导正确的是( )
A. B. C. D.
3.数列满足且,则( )
A. B. C. D.
4.意大利数学家斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,…即,(,),此数列在现代物理、化学等方面都有着广泛的应用,若此数列的每一项被2除后的余数构成一个新数列,则数列的前2020项的和为( )
A.1348 B.1358 C.1347 D.1357
5.设函数的导数为,且,则( )
A.-2 B.0 C.2 D.4
6.从非洲蔓延到东南亚蝗虫灾害严重威胁了国际农业生产,影响了人民生活.世界性与区域性温度的异常、旱涝频繁发生给蝗灾发生创造了机会.已知蝗虫的产卵量y与温度x的关系可以用模型(其中e为自然对数的底数)拟合,设,其变换后得到一组数据:
x 20 23 25 27 30
z 2 2.4 3 3 4.6
由上表可得经验回归方程,则当时,蝗虫的产卵量y的估计值为( )
A. B. C.8 D.
7.已知函数在区间上单调递增,则实数a的最小值为( )
A.1 B.2 C.3 D.4
8.拉格朗日中值定理是微分学的基本定理之一,定理内容如下:如果函数在闭区间上的图象连续不间断,在开区间内的导数为,那么在区间内至少存在一点c,使得成立,其中c叫做在上的“拉格朗日中值点”.根据这个定理,可得函数在上的“拉格朗日中值点”的个数为( )
A.0 B.1 C.2 D.3
二、多项选择题
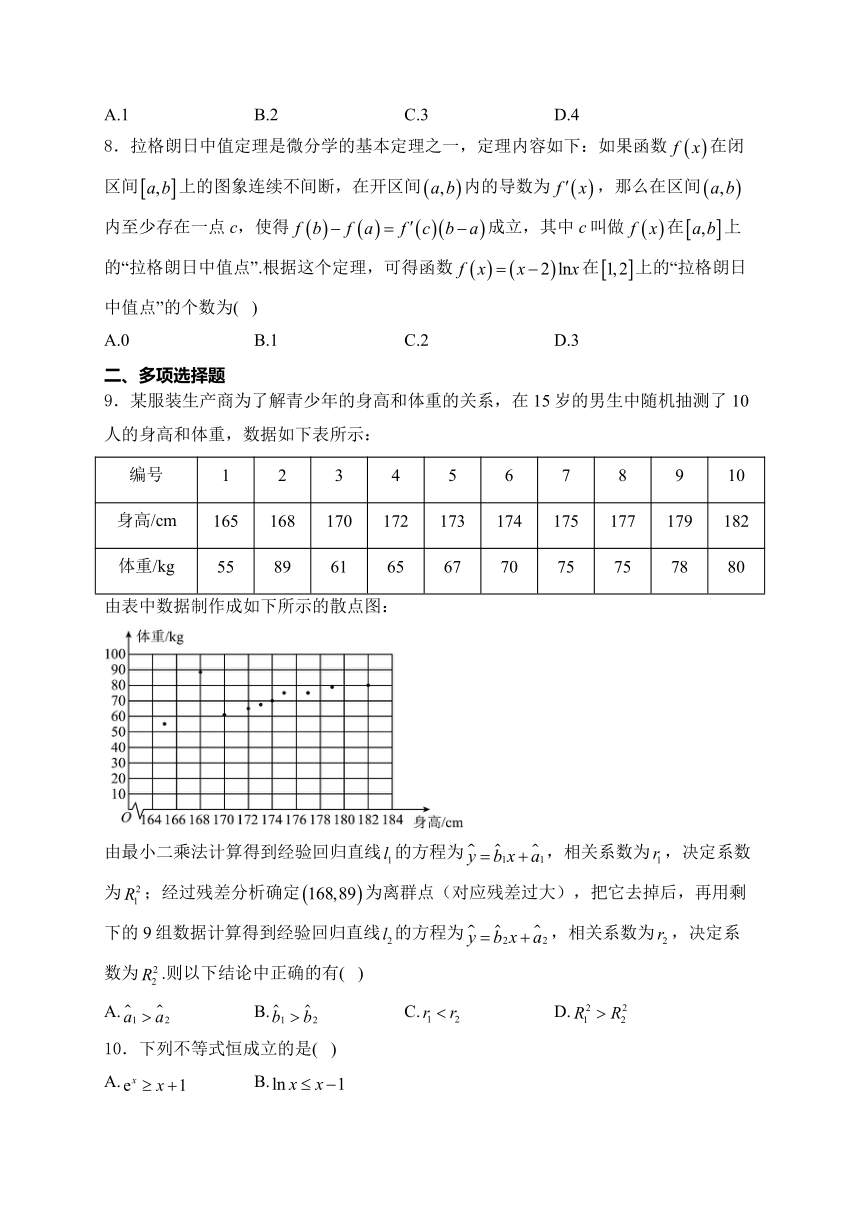
9.某服装生产商为了解青少年的身高和体重的关系,在15岁的男生中随机抽测了10人的身高和体重,数据如下表所示:
编号 1 2 3 4 5 6 7 8 9 10
身高/cm 165 168 170 172 173 174 175 177 179 182
体重/kg 55 89 61 65 67 70 75 75 78 80
由表中数据制作成如下所示的散点图:
由最小二乘法计算得到经验回归直线的方程为,相关系数为,决定系数为;经过残差分析确定为离群点(对应残差过大),把它去掉后,再用剩下的9组数据计算得到经验回归直线的方程为,相关系数为,决定系数为.则以下结论中正确的有( )
A. B. C. D.
10.下列不等式恒成立的是( )
A. B.
C. D.
11.已知数列的前n项和为,下列说法正确的是( )
A.若,则是等差数列
B.若,则是等比数列
C.若,,则数列为递增数列
D.若数列为等差数列,,则最小
三、填空题
12.已知数列的前n项和为,,,则___________.
13.若函数在上单调递减,则实数a的取值范围是________.
四、双空题
14.为各项非零的等差数列,其前n项和为,若对任意正整数n,均有,则的通项公式________;数列的前n项和________.
五、解答题
15.已知函数.
(1)求曲线与直线垂直的切线方程;
(2)若过点的直线l与曲线相切,求直线l的斜率.
16.已知等差数列前n项和为(),数列是等比数列,,,,.
(1)求数列和的通项公式;
(2)若,设数列的前n项和为,求.
17.某企业2015年的纯利润为500万元,因为企业的设备老化等原因,企业的生产能力将逐年下降.若不进行技术改造,预测从2015年开始,此后每年比上一年纯利润减少20万元.如果进行技术改造,2016年初该企业需一次性投入资金600万元,在未扣除技术改造资金的情况下,预计2016年的利润为750万元,此后每年的利润比前一年利润的一半还多250万元.
(1)设从2016年起的第n年(以2016年为第一年),该企业不进行技术改造的年纯利润为万元;进行技术改造后,在未扣除技术改造资金的情况下的年利润为万元,求和;
(2)设从2016年起的第n年(以2016年为第一年),该企业不进行技术改造的累计纯利润为万元,进行技术改造后的累计纯利润为万元,求和;
(3)依上述预测,从2016年起该企业至少经过多少年,进行技术改造的累计纯利润将超过不进行技术改造的累计纯利润
18.2024年1月4日,教育部在京召开全国“双减”工作视频调度会,会议要求进一步提高双减政治站位,将“双减”工作作为重中之重,坚定不移推进,成为受老师和家长关注的重要话题.某学校为了解家长对双减工作的满意程度进行问卷调查(评价结果仅有“满意”、“不满意”),从所有参与评价的对象中随机抽取120人进行调查,部分数据如表所示(单位:人):
满意 不满意 合计
男性 10 50
女性 60
合计 120
(1)请将列联表补充完整,试根据小概率值的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
(2)若将频率视为概率,从所有给出“满意”的家长中随机抽取3人,用随机变量X表示被抽到的男性家长的人数,求X的分布列;
(3)在抽出的120人中,从给出“满意”的家长中利用分层抽样的方法抽取10人,从给出“不满意”的对象中抽取人.现从这人中,随机抽出2人,用随机变量Y表示被抽到的给出“满意”的女性家长的人数.若随机变量Y的数学期望不小于1,求m的最大值.
参考公式:,其中.
参考数据:
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
19.已知函数.
(1)当时,讨论的单调性;
(2)若在点处的切线方程为,若对任意的
恒有,求t的取值范围(e是自然对数的底数).
参考答案
1.答案:C
解析:由题意:,
可得,
所以,
故选:C
2.答案:C
解析:,,
由,可得,
,
是常数,而常数的导数为0,,
故选:C
3.答案:B
解析:因为,可得,
又因为,可得,所以是以1为首项,4为公比的等比数列,
则,所以,所以.
故选:B.
4.答案:C
解析:由数列1,1,2,3,5,8,13,21,34,55,…,各项除以2的余数,可得数列为,1,1,0,1,1,0,1,1,0,
所以数列是周期为3的周期数列,前3项和为,
因为,
所以数列的前2020项的和为
故选:C
5.答案:B
解析:因为,所以,
所以,所以,
所以,所以.
故选:B
6.答案:A
解析:由表格数据知:,,
因为数对满足,得,
,即,,x=35时,.
故当时,蝗虫的产卵量y的估计值为.
故选:A.
7.答案:D
解析:因为在区间上单调递增,
所以在上恒成立,即,
又当时,函数,时取得最大值4,
所以,所以a的最小值为4.
故选:D.
8.答案:B
解析:,令为函数在上的“拉格朗日中值点”,
则,
令,则在上恒成立,
故在上单调递增,
又,,
由零点存在性定理可得:存在唯一的,使得.
故选:B
9.答案:AC
解析:身高的平均数为,
因为离群点的横坐标168小于平均值,纵坐标89相对过大,
所以去掉离群点后经验回归直线的截距变小而斜率变大,
所以,,所以A正确,B错误;
去掉离群点后成对样本数据的线性相关程度更强,拟合效果会更好,
所以,,所以C正确,D错误.
故选:AC.
10.答案:AB
解析:对选项A,设,,
当时,,为减函数,
当时,,为增函数,
所以,即,故A正确
对选项B,设,,
当时,,为增函数,
当时,,为减函数,
所以,即,故B正确.
对选项C,当时,,此时,故C错误.
对选项D,当时,,故D错误.
故选:AB
11.答案:BC
解析:对于选项A,,,,
,不满足是等差数列,故选项A错误;
对于选项B,当时,,
当时,,
因为时也满足上式,所以,则,
所以是等比数列,故选项B正确;
对于选项C,因为,所以,
因为,所以,
因此数列为以为首项,4为公差的等差数列,也是递增数列,故选项C正确;
对于选项D,设数列的公差为d,因为,所以,
即,当时,没有最小值,故选项D错误.
故选:BC.
12.答案:
解析:由题意得,又,则,
故数列是以6为首项,为公比的等比数列,则.
故答案为:.
13.答案:
解析:函数,求导得,由在上单调递减,
得,,而函数在上单调递减,
因此,恒成立,则,
所以实数a的取值范围是.
故答案为:
14.答案:①.;②.
解析:因为为等差数列且,
可得,
又因为,可得,所以,
所以,则,
两式相减得,
,
所以.
故答案为:;.
15.答案:(1)
(2)-3或5
解析:(1)因为斜率为,所以,
所以,又.
所以所求切线方程为,即.
(2),设切点的横坐标为m,直线l的斜率为k,直线l的方程:,
则
则,整理得,所以,
所以或5.
16.答案:(1),;
(2).
解析:(1)设等差数列的公差为d,等比数列的公比为q(),
由,,,,
得,解得,,
所以,.
(2)由(1)知,,
因此当n为奇数时,,当n为偶数时,,
所以
.
17.答案:(1),;
(2),;
(3)至少经过4年,进行技术改造的累计纯利润将超过不进行技术改造的累计纯利润.
解析:(1)由题意得是等差数列,,
所以
由题意得,
所以
所以是首项为250,公比为的等比数列
所以
所以
(2)是数列的前n项和
所以
是数列的前n项和减去600,所以
(3)
易得此函数当时单调递增
且时
时
所以至少经过4年,进行技术改造的累计纯利润
将超过不进行技术改造的累计纯利润.
18.答案:(1)列联表见解析,无关;
(2)分布列见解析;
(3)2
解析:(1)根据题意,得到列联表如下:
满意 不满意 合计
男性 40 10 50
女性 60 10 70
合计 100 20 120
零假设:“对双减工作满意程度的评价与性别无关”,所以没有充分证据证明零假设不成立,所以没有90%的把握认为“对双减工作满意程度的评价与性别有关”.
(2)从所有给出“满意”的家长中随机抽取1人为男性的概率为,
且各次抽取之间相互独立,所以随机变量,
所以,,,,
故随机变量X的分布列为:
X 0 1 2 3
P
(3)从给出“满意”的观众中利用分层抽样的方法抽取10人,
其中男性有人,女性有人,所以随机变量Y的取值为,
可得,,,
则随机变量Y的数学期望,
则,解得,又因为,故m的最大值为2.
19.答案:(1)当时,在R上单调递增;当时,在,上单调递增,在上单调递减;当时,在,上单调递增,在上单调递减;
(2)
解析:(1)当时,,
所以.
令,解得或,
①当时,,所以在R上单调递增;
②当时,,列表得:
x 0
+ 0 - 0 +
↗ ↘ ↗
所以在,上单调递增,在上单调递减;
③当时,,列表得:
x 0
+ 0 - 0 +
↗ ↘ ↗
所以,上单调递增,在上单调递减.
综上可得,当时,在R上单调递增;
当时,在,上单调递增,在上单调递减;
当时,在,上单调递增,在上单调递减.
(2)因为,
所以,
由题意得,
整理得,解得
所以,
因为对任意的恒成立,
所以对任意的恒成立,
设,
则,
所以当时,,单调递减,
当时,,单调递增.
因为,,
所以,
所以,
解得.
所以实数t的取值范围为.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.已知等差数列的公差为4,且,,成等比数列,则( )
A.46 B.48 C.50 D.52
2.下列式子求导正确的是( )
A. B. C. D.
3.数列满足且,则( )
A. B. C. D.
4.意大利数学家斐波那契以兔子繁殖为例,引入“兔子数列”:1,1,2,3,5,8,13,21,34,55,…即,(,),此数列在现代物理、化学等方面都有着广泛的应用,若此数列的每一项被2除后的余数构成一个新数列,则数列的前2020项的和为( )
A.1348 B.1358 C.1347 D.1357
5.设函数的导数为,且,则( )
A.-2 B.0 C.2 D.4
6.从非洲蔓延到东南亚蝗虫灾害严重威胁了国际农业生产,影响了人民生活.世界性与区域性温度的异常、旱涝频繁发生给蝗灾发生创造了机会.已知蝗虫的产卵量y与温度x的关系可以用模型(其中e为自然对数的底数)拟合,设,其变换后得到一组数据:
x 20 23 25 27 30
z 2 2.4 3 3 4.6
由上表可得经验回归方程,则当时,蝗虫的产卵量y的估计值为( )
A. B. C.8 D.
7.已知函数在区间上单调递增,则实数a的最小值为( )
A.1 B.2 C.3 D.4
8.拉格朗日中值定理是微分学的基本定理之一,定理内容如下:如果函数在闭区间上的图象连续不间断,在开区间内的导数为,那么在区间内至少存在一点c,使得成立,其中c叫做在上的“拉格朗日中值点”.根据这个定理,可得函数在上的“拉格朗日中值点”的个数为( )
A.0 B.1 C.2 D.3
二、多项选择题
9.某服装生产商为了解青少年的身高和体重的关系,在15岁的男生中随机抽测了10人的身高和体重,数据如下表所示:
编号 1 2 3 4 5 6 7 8 9 10
身高/cm 165 168 170 172 173 174 175 177 179 182
体重/kg 55 89 61 65 67 70 75 75 78 80
由表中数据制作成如下所示的散点图:
由最小二乘法计算得到经验回归直线的方程为,相关系数为,决定系数为;经过残差分析确定为离群点(对应残差过大),把它去掉后,再用剩下的9组数据计算得到经验回归直线的方程为,相关系数为,决定系数为.则以下结论中正确的有( )
A. B. C. D.
10.下列不等式恒成立的是( )
A. B.
C. D.
11.已知数列的前n项和为,下列说法正确的是( )
A.若,则是等差数列
B.若,则是等比数列
C.若,,则数列为递增数列
D.若数列为等差数列,,则最小
三、填空题
12.已知数列的前n项和为,,,则___________.
13.若函数在上单调递减,则实数a的取值范围是________.
四、双空题
14.为各项非零的等差数列,其前n项和为,若对任意正整数n,均有,则的通项公式________;数列的前n项和________.
五、解答题
15.已知函数.
(1)求曲线与直线垂直的切线方程;
(2)若过点的直线l与曲线相切,求直线l的斜率.
16.已知等差数列前n项和为(),数列是等比数列,,,,.
(1)求数列和的通项公式;
(2)若,设数列的前n项和为,求.
17.某企业2015年的纯利润为500万元,因为企业的设备老化等原因,企业的生产能力将逐年下降.若不进行技术改造,预测从2015年开始,此后每年比上一年纯利润减少20万元.如果进行技术改造,2016年初该企业需一次性投入资金600万元,在未扣除技术改造资金的情况下,预计2016年的利润为750万元,此后每年的利润比前一年利润的一半还多250万元.
(1)设从2016年起的第n年(以2016年为第一年),该企业不进行技术改造的年纯利润为万元;进行技术改造后,在未扣除技术改造资金的情况下的年利润为万元,求和;
(2)设从2016年起的第n年(以2016年为第一年),该企业不进行技术改造的累计纯利润为万元,进行技术改造后的累计纯利润为万元,求和;
(3)依上述预测,从2016年起该企业至少经过多少年,进行技术改造的累计纯利润将超过不进行技术改造的累计纯利润
18.2024年1月4日,教育部在京召开全国“双减”工作视频调度会,会议要求进一步提高双减政治站位,将“双减”工作作为重中之重,坚定不移推进,成为受老师和家长关注的重要话题.某学校为了解家长对双减工作的满意程度进行问卷调查(评价结果仅有“满意”、“不满意”),从所有参与评价的对象中随机抽取120人进行调查,部分数据如表所示(单位:人):
满意 不满意 合计
男性 10 50
女性 60
合计 120
(1)请将列联表补充完整,试根据小概率值的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
(2)若将频率视为概率,从所有给出“满意”的家长中随机抽取3人,用随机变量X表示被抽到的男性家长的人数,求X的分布列;
(3)在抽出的120人中,从给出“满意”的家长中利用分层抽样的方法抽取10人,从给出“不满意”的对象中抽取人.现从这人中,随机抽出2人,用随机变量Y表示被抽到的给出“满意”的女性家长的人数.若随机变量Y的数学期望不小于1,求m的最大值.
参考公式:,其中.
参考数据:
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
19.已知函数.
(1)当时,讨论的单调性;
(2)若在点处的切线方程为,若对任意的
恒有,求t的取值范围(e是自然对数的底数).
参考答案
1.答案:C
解析:由题意:,
可得,
所以,
故选:C
2.答案:C
解析:,,
由,可得,
,
是常数,而常数的导数为0,,
故选:C
3.答案:B
解析:因为,可得,
又因为,可得,所以是以1为首项,4为公比的等比数列,
则,所以,所以.
故选:B.
4.答案:C
解析:由数列1,1,2,3,5,8,13,21,34,55,…,各项除以2的余数,可得数列为,1,1,0,1,1,0,1,1,0,
所以数列是周期为3的周期数列,前3项和为,
因为,
所以数列的前2020项的和为
故选:C
5.答案:B
解析:因为,所以,
所以,所以,
所以,所以.
故选:B
6.答案:A
解析:由表格数据知:,,
因为数对满足,得,
,即,,x=35时,.
故当时,蝗虫的产卵量y的估计值为.
故选:A.
7.答案:D
解析:因为在区间上单调递增,
所以在上恒成立,即,
又当时,函数,时取得最大值4,
所以,所以a的最小值为4.
故选:D.
8.答案:B
解析:,令为函数在上的“拉格朗日中值点”,
则,
令,则在上恒成立,
故在上单调递增,
又,,
由零点存在性定理可得:存在唯一的,使得.
故选:B
9.答案:AC
解析:身高的平均数为,
因为离群点的横坐标168小于平均值,纵坐标89相对过大,
所以去掉离群点后经验回归直线的截距变小而斜率变大,
所以,,所以A正确,B错误;
去掉离群点后成对样本数据的线性相关程度更强,拟合效果会更好,
所以,,所以C正确,D错误.
故选:AC.
10.答案:AB
解析:对选项A,设,,
当时,,为减函数,
当时,,为增函数,
所以,即,故A正确
对选项B,设,,
当时,,为增函数,
当时,,为减函数,
所以,即,故B正确.
对选项C,当时,,此时,故C错误.
对选项D,当时,,故D错误.
故选:AB
11.答案:BC
解析:对于选项A,,,,
,不满足是等差数列,故选项A错误;
对于选项B,当时,,
当时,,
因为时也满足上式,所以,则,
所以是等比数列,故选项B正确;
对于选项C,因为,所以,
因为,所以,
因此数列为以为首项,4为公差的等差数列,也是递增数列,故选项C正确;
对于选项D,设数列的公差为d,因为,所以,
即,当时,没有最小值,故选项D错误.
故选:BC.
12.答案:
解析:由题意得,又,则,
故数列是以6为首项,为公比的等比数列,则.
故答案为:.
13.答案:
解析:函数,求导得,由在上单调递减,
得,,而函数在上单调递减,
因此,恒成立,则,
所以实数a的取值范围是.
故答案为:
14.答案:①.;②.
解析:因为为等差数列且,
可得,
又因为,可得,所以,
所以,则,
两式相减得,
,
所以.
故答案为:;.
15.答案:(1)
(2)-3或5
解析:(1)因为斜率为,所以,
所以,又.
所以所求切线方程为,即.
(2),设切点的横坐标为m,直线l的斜率为k,直线l的方程:,
则
则,整理得,所以,
所以或5.
16.答案:(1),;
(2).
解析:(1)设等差数列的公差为d,等比数列的公比为q(),
由,,,,
得,解得,,
所以,.
(2)由(1)知,,
因此当n为奇数时,,当n为偶数时,,
所以
.
17.答案:(1),;
(2),;
(3)至少经过4年,进行技术改造的累计纯利润将超过不进行技术改造的累计纯利润.
解析:(1)由题意得是等差数列,,
所以
由题意得,
所以
所以是首项为250,公比为的等比数列
所以
所以
(2)是数列的前n项和
所以
是数列的前n项和减去600,所以
(3)
易得此函数当时单调递增
且时
时
所以至少经过4年,进行技术改造的累计纯利润
将超过不进行技术改造的累计纯利润.
18.答案:(1)列联表见解析,无关;
(2)分布列见解析;
(3)2
解析:(1)根据题意,得到列联表如下:
满意 不满意 合计
男性 40 10 50
女性 60 10 70
合计 100 20 120
零假设:“对双减工作满意程度的评价与性别无关”,所以没有充分证据证明零假设不成立,所以没有90%的把握认为“对双减工作满意程度的评价与性别有关”.
(2)从所有给出“满意”的家长中随机抽取1人为男性的概率为,
且各次抽取之间相互独立,所以随机变量,
所以,,,,
故随机变量X的分布列为:
X 0 1 2 3
P
(3)从给出“满意”的观众中利用分层抽样的方法抽取10人,
其中男性有人,女性有人,所以随机变量Y的取值为,
可得,,,
则随机变量Y的数学期望,
则,解得,又因为,故m的最大值为2.
19.答案:(1)当时,在R上单调递增;当时,在,上单调递增,在上单调递减;当时,在,上单调递增,在上单调递减;
(2)
解析:(1)当时,,
所以.
令,解得或,
①当时,,所以在R上单调递增;
②当时,,列表得:
x 0
+ 0 - 0 +
↗ ↘ ↗
所以在,上单调递增,在上单调递减;
③当时,,列表得:
x 0
+ 0 - 0 +
↗ ↘ ↗
所以,上单调递增,在上单调递减.
综上可得,当时,在R上单调递增;
当时,在,上单调递增,在上单调递减;
当时,在,上单调递增,在上单调递减.
(2)因为,
所以,
由题意得,
整理得,解得
所以,
因为对任意的恒成立,
所以对任意的恒成立,
设,
则,
所以当时,,单调递减,
当时,,单调递增.
因为,,
所以,
所以,
解得.
所以实数t的取值范围为.
同课章节目录
