五年级下册数学苏教版第七单元用转化的策略解决问题课件(共26张PPT)
文档属性
| 名称 | 五年级下册数学苏教版第七单元用转化的策略解决问题课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-27 07:44:28 | ||
图片预览








文档简介
(共26张PPT)
7-1 用转化的策略解决问题(1)
3.14×8 =
3.14×0.3 =
3.14× 4 =
3.14× 5 =
3.14× 60 =
3.14× 7 =
3.14× 2.5 =
π× 0.32 =
π× 92 =
π× 302 =
π× 0.72 =
25.12
0.942
12.56
15.7
188.4
21.98
7.85
0.09π
π× 602 =
81π
900π
0.49π
3600π
学过哪些解决问题的策略?
从条件想起、从问题想起
列表整理
画图
一一列举
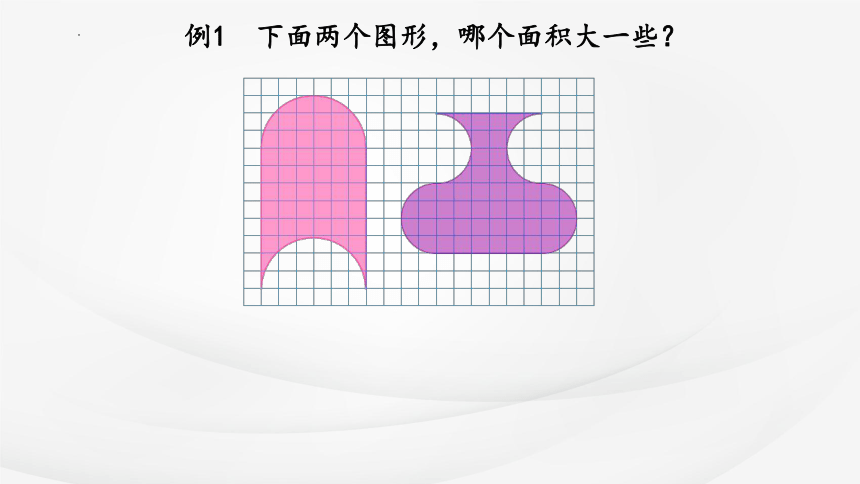
例1 下面两个图形,哪个面积大一些?
方法一:
运用了什么策略?
转化
规则
不规则
将什么转化成了什么?
运用了什么方法?
平移、旋转
转化前后的图形,什么变了什么没变?
形状变了,
大小没变。
回顾解决问题的过程,你有什么体会?
转化后的图形与转化前相比,形状变了,大小没有变。
图形转化时可以运用平移、旋转等方法。
有些不规则的图形可以转化成熟悉的简单的图形。
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
计算小数乘法时,把小数乘法转化成整数乘法。
推导圆面积公式时,把圆转化成长方形。
计算异分母分数加、减法时,把异分母分数转化成同分母分数。
推导平行四边形的面积公式时,把平行四边形转化成长方形。
推导三角形和梯形的面积公式时,把三角形或梯形转化成平行四边形。
计算异分母分数加减法时,把异分母分数转化成同分母分数。
小数乘法可以先转化成整数计算
转化
未知 →
→ 已知
转化
复杂 →
→ 简单
推导圆面积公式时, 把圆转化成长方形。
理一理:
1、平行四边形→长方形;
三角形、梯形→ 平行四边形;
圆→长方形;
2、异分母分数加减法→同分母分数加减法;
(化繁为简、化难为易,化未知为已知)
说一说:这样的转化有什么共同的地方?
形的转化
计算中
“数”的转化
小数乘法→整数乘法;
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
两个图案的面积相等。如上图。
P106 练一练
P109 练习十六
1.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
(5+3)×2
=8×2
=16(厘米)
2.用分数表示各图中的涂色部分。
( )
( )
( )
( )
( )
( )
1
4
1
2
5
8
3.一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米
1×2=2(米)
(45-2)×(27-2)
=43×25
=1075(平方米)
答:草坪的面积是1075平方米。
课堂小结
整体 →
→ 部分
复杂
↓
↓
简单
不规则
↓
↓
规则
↓
↓
未知
已知
转化
4.如图是一块长方形草地,它的长是 16 米,宽是 10 米,中间有两条道路,一条是长方形,另一条是平行四边形,草坪(涂色部分)的面积是多少平方米
(16 -2) ×(10 -2)
= 14×8
=112( 平方米)
答:草坪(涂色部分)的面积是 112 平方米。
***一个羊圈依墙而建,呈半圆形,半径是 5 米,把它的直径增加 2 米。羊圈的面积增加了多少平方米
r : 5+2÷2=6(米)
π×( 62-52)=11π(平方米)
11π÷2 = 5.5π(平方米)
7-1 用转化的策略解决问题(1)
3.14×8 =
3.14×0.3 =
3.14× 4 =
3.14× 5 =
3.14× 60 =
3.14× 7 =
3.14× 2.5 =
π× 0.32 =
π× 92 =
π× 302 =
π× 0.72 =
25.12
0.942
12.56
15.7
188.4
21.98
7.85
0.09π
π× 602 =
81π
900π
0.49π
3600π
学过哪些解决问题的策略?
从条件想起、从问题想起
列表整理
画图
一一列举
例1 下面两个图形,哪个面积大一些?
方法一:
运用了什么策略?
转化
规则
不规则
将什么转化成了什么?
运用了什么方法?
平移、旋转
转化前后的图形,什么变了什么没变?
形状变了,
大小没变。
回顾解决问题的过程,你有什么体会?
转化后的图形与转化前相比,形状变了,大小没有变。
图形转化时可以运用平移、旋转等方法。
有些不规则的图形可以转化成熟悉的简单的图形。
在以前的学习中,我们曾经运用转化的策略解决过哪些问题?
计算小数乘法时,把小数乘法转化成整数乘法。
推导圆面积公式时,把圆转化成长方形。
计算异分母分数加、减法时,把异分母分数转化成同分母分数。
推导平行四边形的面积公式时,把平行四边形转化成长方形。
推导三角形和梯形的面积公式时,把三角形或梯形转化成平行四边形。
计算异分母分数加减法时,把异分母分数转化成同分母分数。
小数乘法可以先转化成整数计算
转化
未知 →
→ 已知
转化
复杂 →
→ 简单
推导圆面积公式时, 把圆转化成长方形。
理一理:
1、平行四边形→长方形;
三角形、梯形→ 平行四边形;
圆→长方形;
2、异分母分数加减法→同分母分数加减法;
(化繁为简、化难为易,化未知为已知)
说一说:这样的转化有什么共同的地方?
形的转化
计算中
“数”的转化
小数乘法→整数乘法;
明明和冬冬在同样大小的长方形纸上分别画了一个图案(图中直条的宽度都相等)。这两个图案的面积相等吗?为什么?
两个图案的面积相等。如上图。
P106 练一练
P109 练习十六
1.观察下面两个图形,要求右边图形的周长,怎样计算比较简便?如果每个小方格的边长是1厘米,右边图形的周长是多少厘米?
(5+3)×2
=8×2
=16(厘米)
2.用分数表示各图中的涂色部分。
( )
( )
( )
( )
( )
( )
1
4
1
2
5
8
3.一块草坪被4条1米宽的小路平均分成了9小块。草坪的面积是多少平方米
1×2=2(米)
(45-2)×(27-2)
=43×25
=1075(平方米)
答:草坪的面积是1075平方米。
课堂小结
整体 →
→ 部分
复杂
↓
↓
简单
不规则
↓
↓
规则
↓
↓
未知
已知
转化
4.如图是一块长方形草地,它的长是 16 米,宽是 10 米,中间有两条道路,一条是长方形,另一条是平行四边形,草坪(涂色部分)的面积是多少平方米
(16 -2) ×(10 -2)
= 14×8
=112( 平方米)
答:草坪(涂色部分)的面积是 112 平方米。
***一个羊圈依墙而建,呈半圆形,半径是 5 米,把它的直径增加 2 米。羊圈的面积增加了多少平方米
r : 5+2÷2=6(米)
π×( 62-52)=11π(平方米)
11π÷2 = 5.5π(平方米)
