北师大版数学九年级下册第一章 直角三角形的边角关系 解答题(含答案)
文档属性
| 名称 | 北师大版数学九年级下册第一章 直角三角形的边角关系 解答题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-27 09:55:09 | ||
图片预览



文档简介
第一章 《直角三角形的边角关系》解答题
第一课时
一、解答题
1.(1);
(2).
2.已知△ABC中的∠A与∠B满足(1-tanA)2+=0.
(1)试判断△ABC的形状;
(2)求(1+sinA)2-2-(3+tanC)0的值.
3.在中,,求的长.
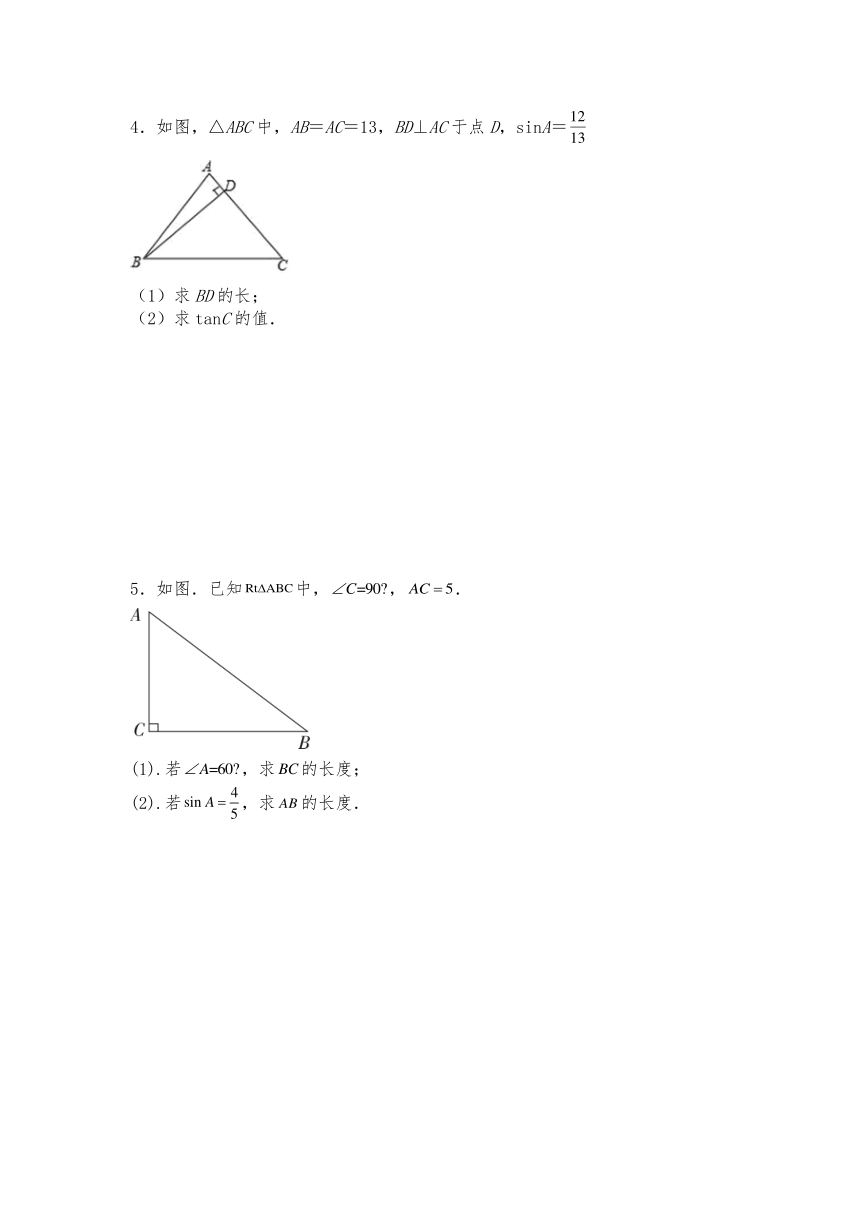
4.如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)求BD的长;
(2)求tanC的值.
5.如图.已知中,,.
(1).若,求的长度;
(2).若,求的长度.
6.如图,在中,已知,,.
(1)用没有刻度的直尺和圆规过点作交的延长线于点保留作图痕迹,不写作法
(2)求的面积.
7.在Rt△ABC中,∠C=90°,点D是BC边的中点,CD=2,tanB=
(1)求AD和AB的长;
(2)求∠B的正弦、余弦值.
8.如图,△ABC中,∠A=30°,∠B=45°,,求AC,BC的长.
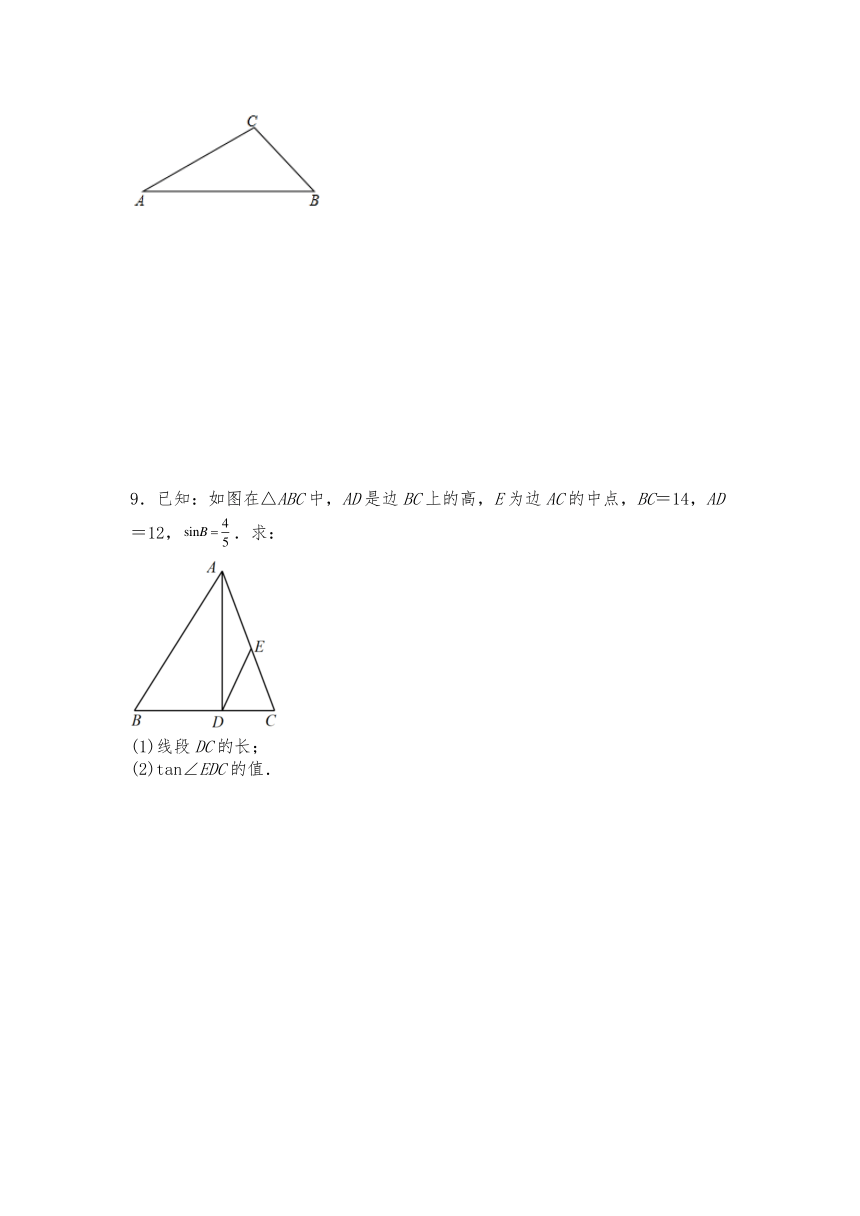
9.已知:如图在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,.求:
(1)线段DC的长;
(2)tan∠EDC的值.
10.如图,甲 乙两楼相距,甲楼高,自甲楼楼顶看乙楼楼顶,仰角为,乙楼有多高?(结果精确到)
11.每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20m),且可绕点B转动,其底部B离地面的距离BC为2m,当云梯顶端A在建筑物EF所在直线上时,底部B到EF的距离BD为9m.
(1)若∠ABD=53°,求此时云梯AB的长.
(2)如图2,若在建筑物底部E的正上方19m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处?请说明理由.
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
12.如图,为测量山高AB,一架无人机在山脚(C处)的正上方(D处),测得山顶(B处)的俯角为30°,若保持飞行高度不变继续行驶2km到达E处,此时测得B,C两处的俯角为45°,60°.
(1)求无人机的飞行高度;
(2)求山高AB.
13.如图,在中,,交于点,且.
(1)求证:四边形是矩形;
(2)的角平分线交于点,当,时,求的长.
14.如图,在对角线BD的延长线上取点E、F,使.连接AE、AF、CE、CF.
(1)求证:四边形AECF是平行四边形;
(2)若,,,,求:的面积.
15.已知点E在△ABC内,,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当时(如图1),
①判断△ABC的形状,并说明理由;
②求证:;
(2)当时(如图2),②的结论还成立吗?若成立,说明理由;若不成立,求出的比值.
第二课时
一、解答题
1.用计算器求下列各式的值(结果精确到0.01):
(1)cos63°17′; (2)tan27.35°;
(3)sin39°57′6″;(4)sin18°+cos55°-tan59°
2.如图1,2分别是某款篮球架的实物图与示意图,于点,底座米,底座与支架所成的角,点在支架上,篮板底部支架.于点,已知米,米,米.
(1)求篮板底部支架与支架所成的的度数.
(2)求篮板底部点到地面的距离,(精确到0.1米)(参考数据:,)
3.如图,已知在锐角三角形ABC中,.
(1)求点C到直线AB的距离;
(2)将绕点A旋转,点B落在点D处,点C落在点E处.
①当点D在边BC上时,联结CE,求的正弦值;
②当时,求点B与点E的距离.
4.某数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=,tanD=tan15°==.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)==.
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度.
5.在平面直角坐标系中,四边形是矩形,点,点,点.以点为旋转中心,逆时针旋转矩形,得到矩形,点,,的对应点分别为,,.记旋转角为.
(1)如图①,当时,求点的坐标;
(2)如图②,当点落在轴的正半轴上时,与交于点求点的坐标;
(3)将矩形旋转一周,求边扫过的面积S(直接写出结果即可).
6.在中,,,点D,E在线段上,点F在的延长线上,连接CD,EF,,.
(1)如图1,当时,线段的数量关系是________;
(2)如图2,当时,请写出线段的数量关系,并说明理由;
(3)在(2)的条件下,当,点E是中点时,请直接写出的面积.
7.如图1,和都是等腰三角形,.
(1)观察发现
请直接写出:的值是______,的值是______;
(2)问题探究
如图2,固定不动,将绕着点O自由旋转,旋转角为,连接BN和AM.的值改变吗?请说明理由;
8.综合与实践
问题情境:数学活动课上,老师出示了一个问题:如图1,在平行四边形ABCD中,,垂足为E,点F为边CD的中点,连接EF,BF,试猜想EF与BF的数量关系,并加以证明;
(1)独立思考:请解答老师提出的问题;
(2)实践探究:希望小组受此问题的启发,将平行四边形ABCD沿着BF(点F为CD的中点)所在直线折叠,如图2,点C的对应点为,连接并延长交AB于点G,请判断AG与BG的数量关系,并加以证明;
(3)问题解决:智慧小组突发奇想,将平行四边形ABCD沿过点B的直线折叠,如图3,点A的对应点为,使于点H,折痕交AD于点M,连接,交CD于点N.该小组提出一个问题:若此ABCD的面积为20,边长,,求图中阴影部分(四边形BHNM)的面积.
9.问题发现
(1)对于任意正实数a,b皆满足 2(请在横线上填写“>”或“<”,“≥”,“≤”,“=”
问题探索
(2)如图1,已知∠MAN=300,点P为内部一点,为等边三角形,点F落在上,点E落在上,过点P作于点C,于点D,设的长为x,的面积为y,若,求y与x之间的函数关系式;
问题解决
(3)如图2,在五边形中,∠B=∠C=90 ,∠MAD=300 ,BC=6,AM=AB=2,点E在边上,点F在边上,∠EDF=600,连接,请问的面积是否存在最小值?若存在,求这个最小值;若不存在,试说明理由.
第一课时答案
一、解答题
1.解:(1)
(2)
.
2.(1)∵|1-tanA)2+|sinB-|=0,
∴tanA=1,sinB=,
∴∠A=45°,∠B=60°,∠C=180°-45°-60°=75°,
∴△ABC是锐角三角形;
(2)∵∠A=45°,∠B=60°,∠C=180°-45°-60°=75°,
∴原式=(1+)2-2-1
=.
3.解: ,
4.解:(1)∵△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
∴
即
解得:BD=12;
(2)∵AC=AB=13,BD=12,BD⊥AC,
∴AD=5,
∴DC=8,
∴tan∠C=
5.(1)
解:中,,
,,
,
,
;
(2)
解:在中,,
,
,,
,
.
6.(1)
解:如图,即为所作的图形;
(2)
在中,,,
,
的面积.
7.(1)
解:∵点D是BC边的中点,CD=2,
∴BC=4.
在Rt△ABC中,
∵tanB=,
∴AC=3.
在Rt△ADC中,
AD=,
AB=.
(2)
解:在Rt△ABC中,
sinB=,cosB=.
8.解:过点C作CD⊥AB,垂足为D,
设CD=x,
在Rt△ACD中,∠A=30°,
,
在Rt△CDB中,∠B=45°,
,
∵AD+BD=AB,
,
∴x=2,
∴CD=2,
∴AC=2CD=4,,
∴AC的长为4,BC的长为.
9.(1)
解:在△ABC中,∵AD是边BC上的高,
∴AD⊥BC.
∴.
∵AD=12,
∴.
在Rt△ABD中,∵,
∴CD=BC﹣BD=14﹣9=5.
(2)
解:在Rt△ADC中,E是AC的中点,
∴DE=EC,
∴∠EDC=∠C.
∴==.
10.解:由题意得:
∠CAE=30°,AE=BD=30m,
在Rt△ACE中,CE=AE tan∠CAE=10m,
故可得乙楼的高度=CE+ED=CE+AB=(40+10)m≈.
11.(1)
解:在Rt△ABD中,∠ABD=53°,BD=9m,
∴AB==15(m),
∴此时云梯AB的长为15m;
(2)
解:在该消防车不移动位置的前提下,云梯能伸到险情处,
理由:由题意得:
DE=BC=2m,
∵AE=19m,
∴AD=AE-DE=19-2=17(m),
在Rt△ABD中,BD=9m,
∴AB= (m),
∵m<20m,
∴在该消防车不移动位置的前提下,云梯能伸到险情处.
12.(1)
在Rt△DCE中,∠DEC=60°,DE=2km,
∴DC=DEtan60°=22(km),
∴无人机的飞行高度为2km;
(2)
延长AB,DE,交于点F,
则AF⊥DF,DC=AF=2km,
设BF=xkm,
在Rt△DFB中,∠FDB=30°,
∴DFxkm,
在Rt△EFB中,∠FEB=45°,
∴EFxkm,
∵DF﹣EF=DE,
∴x﹣x=2,
∴x1,
∴BF=(1)km,
∴AB=AF﹣BF
=2(1)
=(1)km,
∴山高AB为(1)km.
13.(1)
证明:四边形是平行四边形,
,,
,
,
四边形为矩形;
(2)
解:过点作于点,如图所示:
四边形是矩形,
,
,
为的角平分线,
,
,
,
,,
,
,
,
∴,
设,则,
在中,,
,
,
解得:,
.
14.(1)
证明:四边形为平行四边形,
,,
,
,
在和中,
,
,
,,
,
四边形是平行四边形;
(2)
,
,
,
,
,
,
,,
,
,
解得或(舍去),
,
.
15.(1)
解:(1)①判断:△ABC是等边三角形.理由如下:
∵∠ABC=∠ACB=60°
∴∠BAC=180°-∠ABC-∠ACB=60°=∠ABC=∠ACB
∴△ABC是等边三角形.
②△EBD也是等边三角形,理由如下:
如图1,连接DC,
则AB=BC,BE=BD,∠ABE=60°-∠EBC=∠CBD
∴△ABE≌△CBD,
∴AE=CD,∠AEB=∠CDB=150°,
∴∠EDC=150°-∠BDE=90°,
∴在Rt△EDC中,.
(2)
解:如图2:连接DC,
∵∠ABC=∠EBD=90°,∠ACB=∠EDB=60°
∴△ABC∽△EBD
∴,即
又∵∠ABE=90°-∠EBC=∠CBD
∴△ABE∽△CBD,
∴∠AEB=∠CDB=150°,
∴∠EDC=150°-∠BDE=90°,∠CED=∠BEC-∠BED=90°-(90°-∠BDE)=60°
设BD=x在Rt△EBD中DE=2x,BE=
在Rt△EDC中CD=DE×tan60°=2
∴,即.
第二课时答案
一、解答题
1.(1)cos63°17′≈cos63.28°≈0.45;
(2)tan27.35°≈0.52;
(3)sin39°57′≈sin39.95°≈0.64.
(4)sin18°+cos55°-tan59°≈0.3090+0.5736-1.6643≈-0.78.
2..
(1)
∵EF⊥EH,
∴∠HEF=90°,
在Rt△HEF中,HF=米,HE=米,
∴
∴∠FHE=45°,
∴篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)
延长FE交直线BC与点M,过点A作AG⊥FM,垂足为G,
∴∠AGM=∠AGF=90°,
∵ ,
∴FM⊥BC,
∴∠BMG=90°,
∵AB⊥BC,
∴∠ABC=90°,
∴四边形ABMG是矩形,
∴AB=GM,
∵,
∴∠FHE=∠FAG=45°,
∴(米),(米),
∴EG=FG-EF=(米),
在Rt△ABC中,(米),
∴GM=AB=(米),
∴EM=EG+GM=(米),
∴篮板底部点E到地面的距离为2.2米.
3.(1)
解:过点A作AM⊥BC于点M,如图1,
∴ ∠AMB=∠AMC=90°,
在Rt△ABM中,∠B=60°,AB=5,
∴ AM=,,
在Rt△ACM中,AC=7,由勾股定理得,
CM=,
∴,
设点C到直线AB的距离为h,
由,得
,
即点C到直线AB的距离为4;
(2)
解:①将△ABC绕点A旋转,点B落在点D处,点C落在点E处,如图2,
由旋转的性质可知:△ADE≌△ABC,
∴AD=AB=5,∠ADE=∠B=60°,DE=BC=8,
当点D落在边BC上时,∠ADB=∠B=60°,
∴∠CDE=180°-∠ADE-∠ADB=60°,
∵AM⊥BD,
∴DM=BM=,
∴CD=BC-BM-DM=3,
过点C作CN⊥DE于点N,
则∠CND=∠CNE=90°,
在Rt△CDN中,
CN=,,
∴ ,
在Rt△CEN中,由勾股定理得,
,
∴,
即∠CED的正弦值为;
②当ADBC时,过点E作EP⊥BC于点P,交AD于点Q,则∠EQD=∠EPC=∠EPB=90°=∠AMP,
∴四边形AMPQ是矩形,
∴PQ=AM=,PM=AQ,
在Rt△DEQ中,
,,
∴PM=AQ=AD-DQ=1,
若点D在点A的右侧,如图3,
则EP=EQ+PQ=,
∴ BP=BM+PM=,
在Rt△BPE中,由勾股定理得,
BE=;
若点D在点A的左侧,如图4,
则EP=EQ-PQ=,
∴ BP=BM-PM=,
在Rt△BPE中,由勾股定理得,
BE=,
综上所述,点B到点E的距离为或3.
4.(1)
解:方法一:如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=,tan∠DAC=tan75°=.
方法二:根据tan(α±β)=.假设α=30°,β=45°代入差角正切公式:tan75°=tan(30°+45°)=.
(2)
解:在Rt△ABC中,BC=30,AC=60,
∴
∴∠CAB=30°
∵∠CAD=45°
∴∠DAB=75°
在Rt△ABD中,
∴
∴
∴CD的高度为.
5.(1)
∵点A(,0),点C(0,1),
∴OA=,OC=1,
∵四边形OABC是矩形,
∴B(,1),
过D作DG⊥轴于G,
在Rt△ODG中,∠DOG=30,
∴,,
∵,
∴,,
∴点D的坐标为:;
(2)
在Rt△EDO中,ED=1,OD=,
∴OE==2,
∴∠EOD=30,
在Rt△CMO中,∠COM=30,CO=1,
∴,
∴点M的坐标为:;
(3)
根据题意知,边AB扫过的面是一个同心圆环,
,,
.
6.(1)
解:过点F作交AB的延长线于点T.
∵,,,
∴,
∴.
∵,
∴.
∵,
∴.
∵,
∴,
∴.
在和中,
,
∴,
∴;
(2)
解:AC-BE=2BF.
过点D作DG⊥AB交AC于点G,如下图.
∵∠ACB=90°,∠A=30 ,
∴∠ABC=∠AGD=60 , ∠CGD=∠EBF=120 ,
∴.
∵,
∴,
∴GD=BF.
∵∠ACD=∠BEF,∠CGD=∠EBF,
∴△CGD≌△EBF,
∴BE=CG,
∴AC-CG=AG,
∴AC-BE=AG.
∵∠A=30 ,∠GDA=90 ,
∴AG=2GD,
∴AC-BE=2GD,
∴AC-BE=2BF;
(3)
解:作交AB的延长线于点K,过点C作于点H.
∵,,,
∴,
∴,
∴.
∵,
∴,
∴,
∴.
7.(1)
如图1中,过点A作AH⊥OB于H,过点M作MT垂直ON于T.
∵AO=AB,AH⊥OB,
∴OH=HB,
∵∠O=30°,
∴,
∴,
同法可证,,
∴,
故答案为:
(2)
的值不变,理由如下:
由(1)可知:,
∵∠AOB=∠NOM=30°,
∴∠AOB+∠AON=∠NOM+∠AON,
∴∠BON=∠AOM,
∴△BON∽△AOM,
∴.
8.(1)
解:如图,分别延长AD,BF相交于点P,
四边形ABCD是平行四边形,则,
∴,,
点F为边CD的中点,则,
在△PDF和△BCF中,
∴,
∴,
∴,
∴EF为直角三角形BEP斜边中线,则,
∴;
(2)
解:由折叠的性质可得:,,
点F为边CD的中点,则,
∴,
∴,
∵,
∴,
∴,
∴,
四边形ABCD为平行四边形,则,,
∴四边形DGBF为平行四边形,
∴,
∴,
∴;
(3)
解:如图,过点M作ME⊥AB于E,
由折叠性质可得A′B=AB=5,∠A′=∠A,∠ABM=∠A′BM,
ABCD的面积为20,AB=5,则BH=4,
BC=,∠BHC=90°,则CH=,
∴tan∠C=2,
ABCD是平行四边形,则∠A=∠A′=∠C,
Rt△A′HN中,A′H=A′B-BH=AB-BH=1,NH=A′H tan∠A′=2,
△A′HN面积=A′H HN=1,
CD∥AB,A′B⊥CD,则A′B⊥AB,
∵∠ABM=∠A′BM,∠ABM+∠A′BM=90°,
∴∠ABM=45°,
∴△MEB是等腰直角三角形,
设AE=x,则ME=AEtan∠A=2x,BE=ME=2x,
∴AB=AE+BE=3x=5,x=,
∴ME=,
∴△A′BM面积=△ABM面积=AB ME=,
∴四边形MBHN面积=△A′BM面积-△A′HN面积=.
9.(1)
解:∵,
∴,
∴.
故答案为:.
(2)
如图1,设交于点,过点作于点,
∵,
∴,
∵,
∴,
∵,
∴,
∵设的长为,的面积为,
∴,
∵,
∴,
∴,
∴.
∵,
∴,
∵为等边三角形,
∴,
∴,
∴,
∴,
∴,
在中,,
在中,,
∵,
∴.
∴y与x之间的函数关系式为.
(3)
的面积存在最小值,最小值是6,理由如下:
如图2,过点作于,过点作交延长线于,过点作于点,
在中,,
∴,
∴,
∴四边形是矩形,
∴,
∵,
∴,
∴,
∴,
即垂直平分,
∴,
∴,
∵,
∴,
.
设,则
∴
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴.
在中,,
∴,
∴
.
当时,,
由(1)得,
所以当且仅当时,,
∴的面积存在最小值6.
第一课时
一、解答题
1.(1);
(2).
2.已知△ABC中的∠A与∠B满足(1-tanA)2+=0.
(1)试判断△ABC的形状;
(2)求(1+sinA)2-2-(3+tanC)0的值.
3.在中,,求的长.
4.如图,△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
(1)求BD的长;
(2)求tanC的值.
5.如图.已知中,,.
(1).若,求的长度;
(2).若,求的长度.
6.如图,在中,已知,,.
(1)用没有刻度的直尺和圆规过点作交的延长线于点保留作图痕迹,不写作法
(2)求的面积.
7.在Rt△ABC中,∠C=90°,点D是BC边的中点,CD=2,tanB=
(1)求AD和AB的长;
(2)求∠B的正弦、余弦值.
8.如图,△ABC中,∠A=30°,∠B=45°,,求AC,BC的长.
9.已知:如图在△ABC中,AD是边BC上的高,E为边AC的中点,BC=14,AD=12,.求:
(1)线段DC的长;
(2)tan∠EDC的值.
10.如图,甲 乙两楼相距,甲楼高,自甲楼楼顶看乙楼楼顶,仰角为,乙楼有多高?(结果精确到)
11.每年的11月9日是我国的“全国消防安全教育宣传日”,为了提升全民防灾减灾意识,某消防大队进行了消防演习.如图1,架在消防车上的云梯AB可伸缩(最长可伸至20m),且可绕点B转动,其底部B离地面的距离BC为2m,当云梯顶端A在建筑物EF所在直线上时,底部B到EF的距离BD为9m.
(1)若∠ABD=53°,求此时云梯AB的长.
(2)如图2,若在建筑物底部E的正上方19m处突发险情,请问在该消防车不移动位置的前提下,云梯能否伸到险情处?请说明理由.
(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.3)
12.如图,为测量山高AB,一架无人机在山脚(C处)的正上方(D处),测得山顶(B处)的俯角为30°,若保持飞行高度不变继续行驶2km到达E处,此时测得B,C两处的俯角为45°,60°.
(1)求无人机的飞行高度;
(2)求山高AB.
13.如图,在中,,交于点,且.
(1)求证:四边形是矩形;
(2)的角平分线交于点,当,时,求的长.
14.如图,在对角线BD的延长线上取点E、F,使.连接AE、AF、CE、CF.
(1)求证:四边形AECF是平行四边形;
(2)若,,,,求:的面积.
15.已知点E在△ABC内,,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当时(如图1),
①判断△ABC的形状,并说明理由;
②求证:;
(2)当时(如图2),②的结论还成立吗?若成立,说明理由;若不成立,求出的比值.
第二课时
一、解答题
1.用计算器求下列各式的值(结果精确到0.01):
(1)cos63°17′; (2)tan27.35°;
(3)sin39°57′6″;(4)sin18°+cos55°-tan59°
2.如图1,2分别是某款篮球架的实物图与示意图,于点,底座米,底座与支架所成的角,点在支架上,篮板底部支架.于点,已知米,米,米.
(1)求篮板底部支架与支架所成的的度数.
(2)求篮板底部点到地面的距离,(精确到0.1米)(参考数据:,)
3.如图,已知在锐角三角形ABC中,.
(1)求点C到直线AB的距离;
(2)将绕点A旋转,点B落在点D处,点C落在点E处.
①当点D在边BC上时,联结CE,求的正弦值;
②当时,求点B与点E的距离.
4.某数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=,tanD=tan15°==.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)==.
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度.
5.在平面直角坐标系中,四边形是矩形,点,点,点.以点为旋转中心,逆时针旋转矩形,得到矩形,点,,的对应点分别为,,.记旋转角为.
(1)如图①,当时,求点的坐标;
(2)如图②,当点落在轴的正半轴上时,与交于点求点的坐标;
(3)将矩形旋转一周,求边扫过的面积S(直接写出结果即可).
6.在中,,,点D,E在线段上,点F在的延长线上,连接CD,EF,,.
(1)如图1,当时,线段的数量关系是________;
(2)如图2,当时,请写出线段的数量关系,并说明理由;
(3)在(2)的条件下,当,点E是中点时,请直接写出的面积.
7.如图1,和都是等腰三角形,.
(1)观察发现
请直接写出:的值是______,的值是______;
(2)问题探究
如图2,固定不动,将绕着点O自由旋转,旋转角为,连接BN和AM.的值改变吗?请说明理由;
8.综合与实践
问题情境:数学活动课上,老师出示了一个问题:如图1,在平行四边形ABCD中,,垂足为E,点F为边CD的中点,连接EF,BF,试猜想EF与BF的数量关系,并加以证明;
(1)独立思考:请解答老师提出的问题;
(2)实践探究:希望小组受此问题的启发,将平行四边形ABCD沿着BF(点F为CD的中点)所在直线折叠,如图2,点C的对应点为,连接并延长交AB于点G,请判断AG与BG的数量关系,并加以证明;
(3)问题解决:智慧小组突发奇想,将平行四边形ABCD沿过点B的直线折叠,如图3,点A的对应点为,使于点H,折痕交AD于点M,连接,交CD于点N.该小组提出一个问题:若此ABCD的面积为20,边长,,求图中阴影部分(四边形BHNM)的面积.
9.问题发现
(1)对于任意正实数a,b皆满足 2(请在横线上填写“>”或“<”,“≥”,“≤”,“=”
问题探索
(2)如图1,已知∠MAN=300,点P为内部一点,为等边三角形,点F落在上,点E落在上,过点P作于点C,于点D,设的长为x,的面积为y,若,求y与x之间的函数关系式;
问题解决
(3)如图2,在五边形中,∠B=∠C=90 ,∠MAD=300 ,BC=6,AM=AB=2,点E在边上,点F在边上,∠EDF=600,连接,请问的面积是否存在最小值?若存在,求这个最小值;若不存在,试说明理由.
第一课时答案
一、解答题
1.解:(1)
(2)
.
2.(1)∵|1-tanA)2+|sinB-|=0,
∴tanA=1,sinB=,
∴∠A=45°,∠B=60°,∠C=180°-45°-60°=75°,
∴△ABC是锐角三角形;
(2)∵∠A=45°,∠B=60°,∠C=180°-45°-60°=75°,
∴原式=(1+)2-2-1
=.
3.解: ,
4.解:(1)∵△ABC中,AB=AC=13,BD⊥AC于点D,sinA=
∴
即
解得:BD=12;
(2)∵AC=AB=13,BD=12,BD⊥AC,
∴AD=5,
∴DC=8,
∴tan∠C=
5.(1)
解:中,,
,,
,
,
;
(2)
解:在中,,
,
,,
,
.
6.(1)
解:如图,即为所作的图形;
(2)
在中,,,
,
的面积.
7.(1)
解:∵点D是BC边的中点,CD=2,
∴BC=4.
在Rt△ABC中,
∵tanB=,
∴AC=3.
在Rt△ADC中,
AD=,
AB=.
(2)
解:在Rt△ABC中,
sinB=,cosB=.
8.解:过点C作CD⊥AB,垂足为D,
设CD=x,
在Rt△ACD中,∠A=30°,
,
在Rt△CDB中,∠B=45°,
,
∵AD+BD=AB,
,
∴x=2,
∴CD=2,
∴AC=2CD=4,,
∴AC的长为4,BC的长为.
9.(1)
解:在△ABC中,∵AD是边BC上的高,
∴AD⊥BC.
∴.
∵AD=12,
∴.
在Rt△ABD中,∵,
∴CD=BC﹣BD=14﹣9=5.
(2)
解:在Rt△ADC中,E是AC的中点,
∴DE=EC,
∴∠EDC=∠C.
∴==.
10.解:由题意得:
∠CAE=30°,AE=BD=30m,
在Rt△ACE中,CE=AE tan∠CAE=10m,
故可得乙楼的高度=CE+ED=CE+AB=(40+10)m≈.
11.(1)
解:在Rt△ABD中,∠ABD=53°,BD=9m,
∴AB==15(m),
∴此时云梯AB的长为15m;
(2)
解:在该消防车不移动位置的前提下,云梯能伸到险情处,
理由:由题意得:
DE=BC=2m,
∵AE=19m,
∴AD=AE-DE=19-2=17(m),
在Rt△ABD中,BD=9m,
∴AB= (m),
∵m<20m,
∴在该消防车不移动位置的前提下,云梯能伸到险情处.
12.(1)
在Rt△DCE中,∠DEC=60°,DE=2km,
∴DC=DEtan60°=22(km),
∴无人机的飞行高度为2km;
(2)
延长AB,DE,交于点F,
则AF⊥DF,DC=AF=2km,
设BF=xkm,
在Rt△DFB中,∠FDB=30°,
∴DFxkm,
在Rt△EFB中,∠FEB=45°,
∴EFxkm,
∵DF﹣EF=DE,
∴x﹣x=2,
∴x1,
∴BF=(1)km,
∴AB=AF﹣BF
=2(1)
=(1)km,
∴山高AB为(1)km.
13.(1)
证明:四边形是平行四边形,
,,
,
,
四边形为矩形;
(2)
解:过点作于点,如图所示:
四边形是矩形,
,
,
为的角平分线,
,
,
,
,,
,
,
,
∴,
设,则,
在中,,
,
,
解得:,
.
14.(1)
证明:四边形为平行四边形,
,,
,
,
在和中,
,
,
,,
,
四边形是平行四边形;
(2)
,
,
,
,
,
,
,,
,
,
解得或(舍去),
,
.
15.(1)
解:(1)①判断:△ABC是等边三角形.理由如下:
∵∠ABC=∠ACB=60°
∴∠BAC=180°-∠ABC-∠ACB=60°=∠ABC=∠ACB
∴△ABC是等边三角形.
②△EBD也是等边三角形,理由如下:
如图1,连接DC,
则AB=BC,BE=BD,∠ABE=60°-∠EBC=∠CBD
∴△ABE≌△CBD,
∴AE=CD,∠AEB=∠CDB=150°,
∴∠EDC=150°-∠BDE=90°,
∴在Rt△EDC中,.
(2)
解:如图2:连接DC,
∵∠ABC=∠EBD=90°,∠ACB=∠EDB=60°
∴△ABC∽△EBD
∴,即
又∵∠ABE=90°-∠EBC=∠CBD
∴△ABE∽△CBD,
∴∠AEB=∠CDB=150°,
∴∠EDC=150°-∠BDE=90°,∠CED=∠BEC-∠BED=90°-(90°-∠BDE)=60°
设BD=x在Rt△EBD中DE=2x,BE=
在Rt△EDC中CD=DE×tan60°=2
∴,即.
第二课时答案
一、解答题
1.(1)cos63°17′≈cos63.28°≈0.45;
(2)tan27.35°≈0.52;
(3)sin39°57′≈sin39.95°≈0.64.
(4)sin18°+cos55°-tan59°≈0.3090+0.5736-1.6643≈-0.78.
2..
(1)
∵EF⊥EH,
∴∠HEF=90°,
在Rt△HEF中,HF=米,HE=米,
∴
∴∠FHE=45°,
∴篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)
延长FE交直线BC与点M,过点A作AG⊥FM,垂足为G,
∴∠AGM=∠AGF=90°,
∵ ,
∴FM⊥BC,
∴∠BMG=90°,
∵AB⊥BC,
∴∠ABC=90°,
∴四边形ABMG是矩形,
∴AB=GM,
∵,
∴∠FHE=∠FAG=45°,
∴(米),(米),
∴EG=FG-EF=(米),
在Rt△ABC中,(米),
∴GM=AB=(米),
∴EM=EG+GM=(米),
∴篮板底部点E到地面的距离为2.2米.
3.(1)
解:过点A作AM⊥BC于点M,如图1,
∴ ∠AMB=∠AMC=90°,
在Rt△ABM中,∠B=60°,AB=5,
∴ AM=,,
在Rt△ACM中,AC=7,由勾股定理得,
CM=,
∴,
设点C到直线AB的距离为h,
由,得
,
即点C到直线AB的距离为4;
(2)
解:①将△ABC绕点A旋转,点B落在点D处,点C落在点E处,如图2,
由旋转的性质可知:△ADE≌△ABC,
∴AD=AB=5,∠ADE=∠B=60°,DE=BC=8,
当点D落在边BC上时,∠ADB=∠B=60°,
∴∠CDE=180°-∠ADE-∠ADB=60°,
∵AM⊥BD,
∴DM=BM=,
∴CD=BC-BM-DM=3,
过点C作CN⊥DE于点N,
则∠CND=∠CNE=90°,
在Rt△CDN中,
CN=,,
∴ ,
在Rt△CEN中,由勾股定理得,
,
∴,
即∠CED的正弦值为;
②当ADBC时,过点E作EP⊥BC于点P,交AD于点Q,则∠EQD=∠EPC=∠EPB=90°=∠AMP,
∴四边形AMPQ是矩形,
∴PQ=AM=,PM=AQ,
在Rt△DEQ中,
,,
∴PM=AQ=AD-DQ=1,
若点D在点A的右侧,如图3,
则EP=EQ+PQ=,
∴ BP=BM+PM=,
在Rt△BPE中,由勾股定理得,
BE=;
若点D在点A的左侧,如图4,
则EP=EQ-PQ=,
∴ BP=BM-PM=,
在Rt△BPE中,由勾股定理得,
BE=,
综上所述,点B到点E的距离为或3.
4.(1)
解:方法一:如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=,tan∠DAC=tan75°=.
方法二:根据tan(α±β)=.假设α=30°,β=45°代入差角正切公式:tan75°=tan(30°+45°)=.
(2)
解:在Rt△ABC中,BC=30,AC=60,
∴
∴∠CAB=30°
∵∠CAD=45°
∴∠DAB=75°
在Rt△ABD中,
∴
∴
∴CD的高度为.
5.(1)
∵点A(,0),点C(0,1),
∴OA=,OC=1,
∵四边形OABC是矩形,
∴B(,1),
过D作DG⊥轴于G,
在Rt△ODG中,∠DOG=30,
∴,,
∵,
∴,,
∴点D的坐标为:;
(2)
在Rt△EDO中,ED=1,OD=,
∴OE==2,
∴∠EOD=30,
在Rt△CMO中,∠COM=30,CO=1,
∴,
∴点M的坐标为:;
(3)
根据题意知,边AB扫过的面是一个同心圆环,
,,
.
6.(1)
解:过点F作交AB的延长线于点T.
∵,,,
∴,
∴.
∵,
∴.
∵,
∴.
∵,
∴,
∴.
在和中,
,
∴,
∴;
(2)
解:AC-BE=2BF.
过点D作DG⊥AB交AC于点G,如下图.
∵∠ACB=90°,∠A=30 ,
∴∠ABC=∠AGD=60 , ∠CGD=∠EBF=120 ,
∴.
∵,
∴,
∴GD=BF.
∵∠ACD=∠BEF,∠CGD=∠EBF,
∴△CGD≌△EBF,
∴BE=CG,
∴AC-CG=AG,
∴AC-BE=AG.
∵∠A=30 ,∠GDA=90 ,
∴AG=2GD,
∴AC-BE=2GD,
∴AC-BE=2BF;
(3)
解:作交AB的延长线于点K,过点C作于点H.
∵,,,
∴,
∴,
∴.
∵,
∴,
∴,
∴.
7.(1)
如图1中,过点A作AH⊥OB于H,过点M作MT垂直ON于T.
∵AO=AB,AH⊥OB,
∴OH=HB,
∵∠O=30°,
∴,
∴,
同法可证,,
∴,
故答案为:
(2)
的值不变,理由如下:
由(1)可知:,
∵∠AOB=∠NOM=30°,
∴∠AOB+∠AON=∠NOM+∠AON,
∴∠BON=∠AOM,
∴△BON∽△AOM,
∴.
8.(1)
解:如图,分别延长AD,BF相交于点P,
四边形ABCD是平行四边形,则,
∴,,
点F为边CD的中点,则,
在△PDF和△BCF中,
∴,
∴,
∴,
∴EF为直角三角形BEP斜边中线,则,
∴;
(2)
解:由折叠的性质可得:,,
点F为边CD的中点,则,
∴,
∴,
∵,
∴,
∴,
∴,
四边形ABCD为平行四边形,则,,
∴四边形DGBF为平行四边形,
∴,
∴,
∴;
(3)
解:如图,过点M作ME⊥AB于E,
由折叠性质可得A′B=AB=5,∠A′=∠A,∠ABM=∠A′BM,
ABCD的面积为20,AB=5,则BH=4,
BC=,∠BHC=90°,则CH=,
∴tan∠C=2,
ABCD是平行四边形,则∠A=∠A′=∠C,
Rt△A′HN中,A′H=A′B-BH=AB-BH=1,NH=A′H tan∠A′=2,
△A′HN面积=A′H HN=1,
CD∥AB,A′B⊥CD,则A′B⊥AB,
∵∠ABM=∠A′BM,∠ABM+∠A′BM=90°,
∴∠ABM=45°,
∴△MEB是等腰直角三角形,
设AE=x,则ME=AEtan∠A=2x,BE=ME=2x,
∴AB=AE+BE=3x=5,x=,
∴ME=,
∴△A′BM面积=△ABM面积=AB ME=,
∴四边形MBHN面积=△A′BM面积-△A′HN面积=.
9.(1)
解:∵,
∴,
∴.
故答案为:.
(2)
如图1,设交于点,过点作于点,
∵,
∴,
∵,
∴,
∵,
∴,
∵设的长为,的面积为,
∴,
∵,
∴,
∴,
∴.
∵,
∴,
∵为等边三角形,
∴,
∴,
∴,
∴,
∴,
在中,,
在中,,
∵,
∴.
∴y与x之间的函数关系式为.
(3)
的面积存在最小值,最小值是6,理由如下:
如图2,过点作于,过点作交延长线于,过点作于点,
在中,,
∴,
∴,
∴四边形是矩形,
∴,
∵,
∴,
∴,
∴,
即垂直平分,
∴,
∴,
∵,
∴,
.
设,则
∴
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴.
在中,,
∴,
∴
.
当时,,
由(1)得,
所以当且仅当时,,
∴的面积存在最小值6.
