人教版八年级下册数学第18章平行四边形动点问题专题练习(含答案)
文档属性
| 名称 | 人教版八年级下册数学第18章平行四边形动点问题专题练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-27 00:00:00 | ||
图片预览



文档简介
人教版八年级下册数学第18章平行四边形期末动点问题压轴题
1.如图,在四边形中, ,, ,,.点从点出发,以1cm/s的速度向点D运动,点Q从点C出发,以3cm/s的速度向点B同时运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设P,Q运动的时间为ts.
(1)若点P和点Q同时运动了6秒,与有什么数量关系?并说明理由;
(2)在整个运动过程中是否存在t值,使得四边形是矩形?若存在,请求出t值;若不存在,请说明理由;
(3)在整个运动过程中,是否存在一个时间,使得四边形是菱形?如果存在,求出时间t的值,如果不存在,请说明理由.
2.【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形中,是的中点,,与正方形的外角的平分线交于点.试猜想与的数量关系,并加以证明;
(1)【思考尝试】:有同学发现,取的中点,连接可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
(2)【实践探究】:有同学受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形中,为边上一动点(点与不重合),当是等腰直角三角形,,连接可以求出的大小,请你思考并解答这个问题.
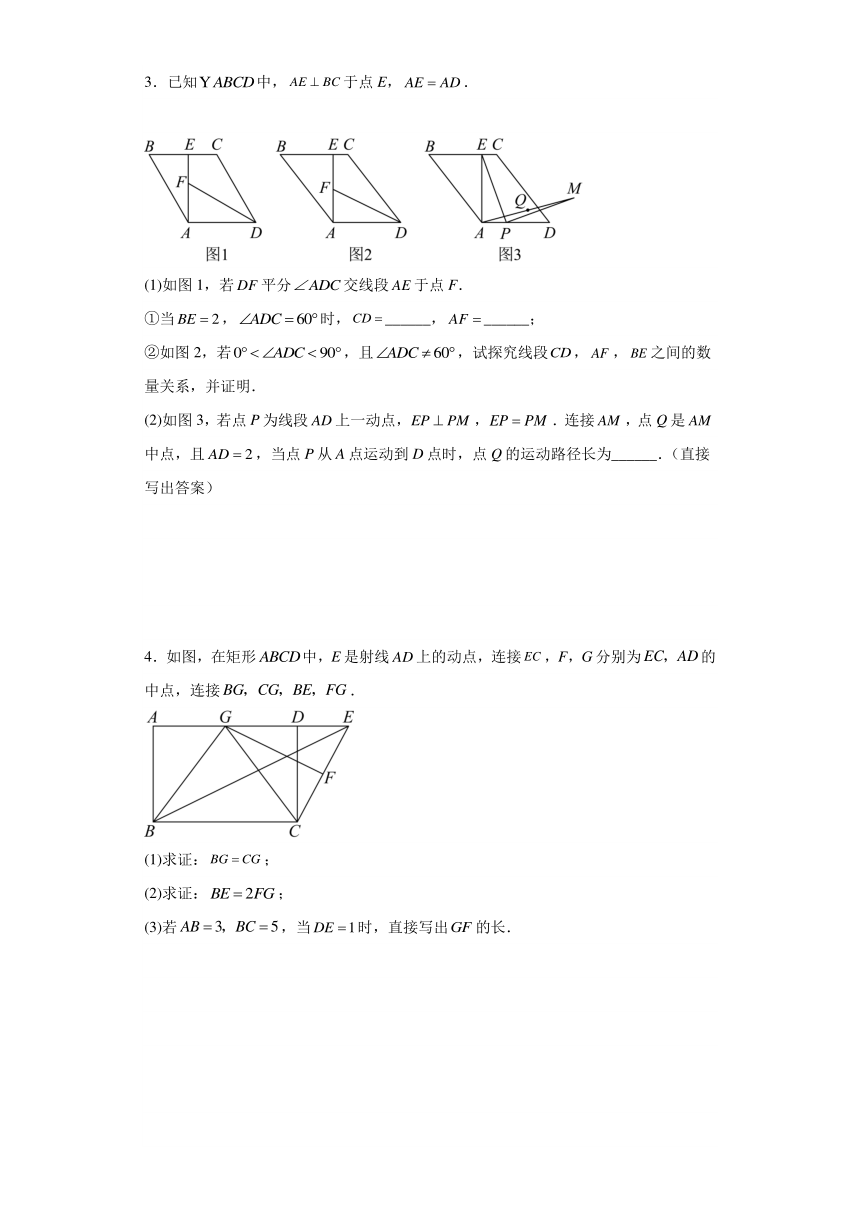
3.已知中,于点E,.
(1)如图1,若平分交线段于点F.
①当,时,______,______;
②如图2,若,且,试探究线段,,之间的数量关系,并证明.
(2)如图3,若点P为线段上一动点,,.连接,点Q是中点,且,当点P从A点运动到D点时,点Q的运动路径长为______.(直接写出答案)
4.如图,在矩形中,E是射线上的动点,连接,F,G分别为的中点,连接.
(1)求证:;
(2)求证:;
(3)若,当时,直接写出的长.
5.如图在中,,是边上的高,且的面积为24.动点P、Q分别从点A、C同时出发,均以每秒1个单位长度的速度分别沿、向终点B、D运动,设点P运动的时间为t秒.
(1)求的长;
(2)求证:四边形是平行四边形;
(3)当四边形是矩形时,求t的值;
(4)当以点A、B、C、D、P、Q中的四个点为顶点的四边形是菱形时,直接写出t的值.
6.点P是平行四边形的对角线所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线作垂线,垂足分别为点E、F.点O为的中点.
(1)如图1,当点P与点O重合时,线段和的数量关系是 ;
(2)当点P运动到如图2所示的位置时,请通过证明判断(1)中的结论是否仍然成立?如果成立请给予证明,如果不成立请说明理由;
(3)如图3,点P在线段的延长线上运动,当时,试探究线段之间的关系.
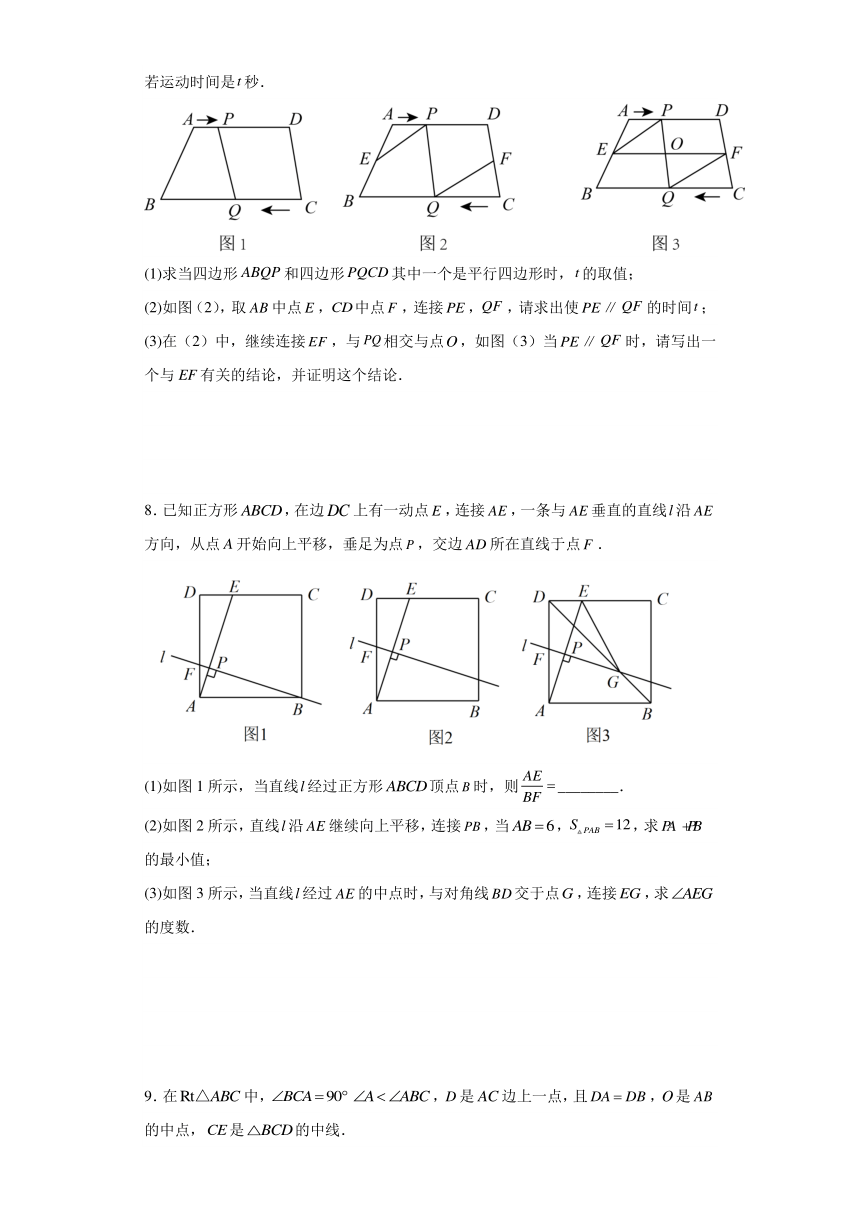
7.如图(1),在四边形中,,,,有动点从点出发,在线段上以的速度向点运动,有动点同时从点出发,在线段上以的速度向点运动,当其中一点到达时,另一点也随之停止运动.连接,若运动时间是秒.
(1)求当四边形和四边形其中一个是平行四边形时,的取值;
(2)如图(2),取中点,中点,连接,,请求出使的时间;
(3)在(2)中,继续连接,与相交与点,如图(3)当时,请写出一个与EF有关的结论,并证明这个结论.
8.已知正方形,在边上有一动点,连接,一条与垂直的直线沿方向,从点A开始向上平移,垂足为点,交边所在直线于点.
(1)如图1所示,当直线经过正方形顶点时,则________.
(2)如图2所示,直线沿继续向上平移,连接,当,,求的最小值;
(3)如图3所示,当直线经过的中点时,与对角线交于点,连接,求的度数.
9.在中,,是边上一点,且,是的中点,是的中线.
(1)如图,连接,证明;
(2)如图,点是射线上的一个动点,将射线绕点逆时针旋转得射线,使,与射线交于点.
猜想并证明线段和线段之间的数量关系;
若,,当时,请直接写出线段的长度(用含的式子表示).
10.如图1,将矩形放置于第一象限,使其顶点O位于原点,且点B,C分别位于x轴,y轴上.若满足.
(1)求点A的坐标;
(2)取中点M,连接,与关于所在直线对称,连接并延长,交x轴于点P.
①求的长;
②如图2,点D位于线段上,且.点E为平面内一动点,满足,连接.请你求出线段长度的最大值.
11.已知在平行四边形中,是边的中点,是边上一动点.
(1)如图1,连接并延长交的延长线于点,求证:是的中点;
(2)如图2,若,,求证:;
(3)如图3,若,,时,是射线上一个动点,将逆时针旋转得到,连接,求的最小值.
12.如图1,中,,,,点P、Q是边,上两个动点,且,以,为邻边作平行四边形,,分别交于点E,F,设.
(1)直接写出 ; .(用含m的代数式表示)
(2)当平行四边形的面积为时,求m的值;
(3)求证:;
(4)如图2,连接,,,当与的一边平行时,求的面积.
13.点是正方形对角线上一动点,点在射线上,且,连接,为中点.
(1)如图1,当点在线段上时,连接交于点,
①试判断的形状,并说明理由;
②若正方形边长为,当点为的中点,则的长为 .
(2)如图2,当点在线段上时,试探究线段,,的等量关系,并说明理由.
(3)若,连接,取的中点,则当点从点运动到点时,点所经过的路径长为 .
14.如图,中,,O为上一动点(不与A、C重合),以每秒2个单位的速度从A向C运动,过点O作直线,直线l与的平分线相交于点E,与的平分线相交于点F.
(1)求证:;
(2)t为何值时,四边形是矩形?请说明理由;
(3)当满足条件______时,(2)中的四边形是正方形.
15.【探究与证明】
在正方形中,G是射线上一动点(不与点A,C重合),连接,作,且使,连接、.
(1)如图1,若点G在上,则:
①图中与全等的三角形是 ;
②线段,,之间的数量关系是 ;
(2)如图2,若G在的延长线上,那么线段,,之间有怎样的数量关系?写出结论,并给出证明.
16.在正方形中,E为射线上一动点(点E不与A,B重合),作,交直线于点F,连接.
(1)如图1,当点E在线段上时,用等式表示线段,,的数量关系;
(2)如图2,当点E在线段的延长线上时,
①依题意补全图2;
②用等式表示线段,,的数量关系,并证明.
17.在矩形中,,,点是边上一动点(不与点B、C重合),将沿直线折叠得到,直线交直线于点.
(1)如图1,当点是的中点时,求的值;
(2)如图1,连接,求周长的最小值;
(3)如图2,延长,交的延长线于点,连接,若点,分别为,的中点,连接交于点,求证;.
18.数学活动课上,老师给出如下定义:如果一个矩形的其中一边是另一边的倍,那么称这个矩形为“和谐矩形”.如图,在矩形中,,则矩形是“和谐矩形”.是边上任意一点,连接,作的垂直平分线分别交于点与的交点为,连接和.
(1)试判断四边形的形状,并说明理由;
(2)如图,在“和谐矩形”中,若AB=4,且是边上一个动点,把沿折叠.点A落在点处,若恰在矩形的对称轴上,则的长为______;
(3)如图,记四边形的面积为,“和谐矩形”的面积为,且 ,若(a为常数),且,求的长.(用含有的代数式表示)
参考答案:
1.(1),
(2)存在,当时,四边形是矩形,
(3)不存在,
2.(1) ,
(2)
3.(1)①4,2;②,
(2)
4.(3)
5.(1)
(3)3
(4)
6.(1)
(2)仍然成立,
(3)
7.(1)或
(2)
(3)和互相平分,
8.(1)1
(2)10
(3)
9.(2)①②或
10.(1)
(2)①;②
11.(3)
12.(1);
(2)
(4)或
13.(1)①是等腰直角三角形,②
(2)
(3)
14.(2),
(3)
15.(1)①;②
(2),
16.(1)
(2)②;
17.(1)
(2)12
18.(1)四边形是菱形,
(2)或
(3)
1.如图,在四边形中, ,, ,,.点从点出发,以1cm/s的速度向点D运动,点Q从点C出发,以3cm/s的速度向点B同时运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设P,Q运动的时间为ts.
(1)若点P和点Q同时运动了6秒,与有什么数量关系?并说明理由;
(2)在整个运动过程中是否存在t值,使得四边形是矩形?若存在,请求出t值;若不存在,请说明理由;
(3)在整个运动过程中,是否存在一个时间,使得四边形是菱形?如果存在,求出时间t的值,如果不存在,请说明理由.
2.【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形中,是的中点,,与正方形的外角的平分线交于点.试猜想与的数量关系,并加以证明;
(1)【思考尝试】:有同学发现,取的中点,连接可以解决这个问题.请在图1中补全图形,解答老师提出的问题.
(2)【实践探究】:有同学受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形中,为边上一动点(点与不重合),当是等腰直角三角形,,连接可以求出的大小,请你思考并解答这个问题.
3.已知中,于点E,.
(1)如图1,若平分交线段于点F.
①当,时,______,______;
②如图2,若,且,试探究线段,,之间的数量关系,并证明.
(2)如图3,若点P为线段上一动点,,.连接,点Q是中点,且,当点P从A点运动到D点时,点Q的运动路径长为______.(直接写出答案)
4.如图,在矩形中,E是射线上的动点,连接,F,G分别为的中点,连接.
(1)求证:;
(2)求证:;
(3)若,当时,直接写出的长.
5.如图在中,,是边上的高,且的面积为24.动点P、Q分别从点A、C同时出发,均以每秒1个单位长度的速度分别沿、向终点B、D运动,设点P运动的时间为t秒.
(1)求的长;
(2)求证:四边形是平行四边形;
(3)当四边形是矩形时,求t的值;
(4)当以点A、B、C、D、P、Q中的四个点为顶点的四边形是菱形时,直接写出t的值.
6.点P是平行四边形的对角线所在直线上的一个动点(点P不与点A、C重合),分别过点A、C向直线作垂线,垂足分别为点E、F.点O为的中点.
(1)如图1,当点P与点O重合时,线段和的数量关系是 ;
(2)当点P运动到如图2所示的位置时,请通过证明判断(1)中的结论是否仍然成立?如果成立请给予证明,如果不成立请说明理由;
(3)如图3,点P在线段的延长线上运动,当时,试探究线段之间的关系.
7.如图(1),在四边形中,,,,有动点从点出发,在线段上以的速度向点运动,有动点同时从点出发,在线段上以的速度向点运动,当其中一点到达时,另一点也随之停止运动.连接,若运动时间是秒.
(1)求当四边形和四边形其中一个是平行四边形时,的取值;
(2)如图(2),取中点,中点,连接,,请求出使的时间;
(3)在(2)中,继续连接,与相交与点,如图(3)当时,请写出一个与EF有关的结论,并证明这个结论.
8.已知正方形,在边上有一动点,连接,一条与垂直的直线沿方向,从点A开始向上平移,垂足为点,交边所在直线于点.
(1)如图1所示,当直线经过正方形顶点时,则________.
(2)如图2所示,直线沿继续向上平移,连接,当,,求的最小值;
(3)如图3所示,当直线经过的中点时,与对角线交于点,连接,求的度数.
9.在中,,是边上一点,且,是的中点,是的中线.
(1)如图,连接,证明;
(2)如图,点是射线上的一个动点,将射线绕点逆时针旋转得射线,使,与射线交于点.
猜想并证明线段和线段之间的数量关系;
若,,当时,请直接写出线段的长度(用含的式子表示).
10.如图1,将矩形放置于第一象限,使其顶点O位于原点,且点B,C分别位于x轴,y轴上.若满足.
(1)求点A的坐标;
(2)取中点M,连接,与关于所在直线对称,连接并延长,交x轴于点P.
①求的长;
②如图2,点D位于线段上,且.点E为平面内一动点,满足,连接.请你求出线段长度的最大值.
11.已知在平行四边形中,是边的中点,是边上一动点.
(1)如图1,连接并延长交的延长线于点,求证:是的中点;
(2)如图2,若,,求证:;
(3)如图3,若,,时,是射线上一个动点,将逆时针旋转得到,连接,求的最小值.
12.如图1,中,,,,点P、Q是边,上两个动点,且,以,为邻边作平行四边形,,分别交于点E,F,设.
(1)直接写出 ; .(用含m的代数式表示)
(2)当平行四边形的面积为时,求m的值;
(3)求证:;
(4)如图2,连接,,,当与的一边平行时,求的面积.
13.点是正方形对角线上一动点,点在射线上,且,连接,为中点.
(1)如图1,当点在线段上时,连接交于点,
①试判断的形状,并说明理由;
②若正方形边长为,当点为的中点,则的长为 .
(2)如图2,当点在线段上时,试探究线段,,的等量关系,并说明理由.
(3)若,连接,取的中点,则当点从点运动到点时,点所经过的路径长为 .
14.如图,中,,O为上一动点(不与A、C重合),以每秒2个单位的速度从A向C运动,过点O作直线,直线l与的平分线相交于点E,与的平分线相交于点F.
(1)求证:;
(2)t为何值时,四边形是矩形?请说明理由;
(3)当满足条件______时,(2)中的四边形是正方形.
15.【探究与证明】
在正方形中,G是射线上一动点(不与点A,C重合),连接,作,且使,连接、.
(1)如图1,若点G在上,则:
①图中与全等的三角形是 ;
②线段,,之间的数量关系是 ;
(2)如图2,若G在的延长线上,那么线段,,之间有怎样的数量关系?写出结论,并给出证明.
16.在正方形中,E为射线上一动点(点E不与A,B重合),作,交直线于点F,连接.
(1)如图1,当点E在线段上时,用等式表示线段,,的数量关系;
(2)如图2,当点E在线段的延长线上时,
①依题意补全图2;
②用等式表示线段,,的数量关系,并证明.
17.在矩形中,,,点是边上一动点(不与点B、C重合),将沿直线折叠得到,直线交直线于点.
(1)如图1,当点是的中点时,求的值;
(2)如图1,连接,求周长的最小值;
(3)如图2,延长,交的延长线于点,连接,若点,分别为,的中点,连接交于点,求证;.
18.数学活动课上,老师给出如下定义:如果一个矩形的其中一边是另一边的倍,那么称这个矩形为“和谐矩形”.如图,在矩形中,,则矩形是“和谐矩形”.是边上任意一点,连接,作的垂直平分线分别交于点与的交点为,连接和.
(1)试判断四边形的形状,并说明理由;
(2)如图,在“和谐矩形”中,若AB=4,且是边上一个动点,把沿折叠.点A落在点处,若恰在矩形的对称轴上,则的长为______;
(3)如图,记四边形的面积为,“和谐矩形”的面积为,且 ,若(a为常数),且,求的长.(用含有的代数式表示)
参考答案:
1.(1),
(2)存在,当时,四边形是矩形,
(3)不存在,
2.(1) ,
(2)
3.(1)①4,2;②,
(2)
4.(3)
5.(1)
(3)3
(4)
6.(1)
(2)仍然成立,
(3)
7.(1)或
(2)
(3)和互相平分,
8.(1)1
(2)10
(3)
9.(2)①②或
10.(1)
(2)①;②
11.(3)
12.(1);
(2)
(4)或
13.(1)①是等腰直角三角形,②
(2)
(3)
14.(2),
(3)
15.(1)①;②
(2),
16.(1)
(2)②;
17.(1)
(2)12
18.(1)四边形是菱形,
(2)或
(3)
