第八单元数学广角——数与形同步练习 人教版数学六年级上册(含答案)
文档属性
| 名称 | 第八单元数学广角——数与形同步练习 人教版数学六年级上册(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 924.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-28 08:40:29 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八单元数学广角——数与形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
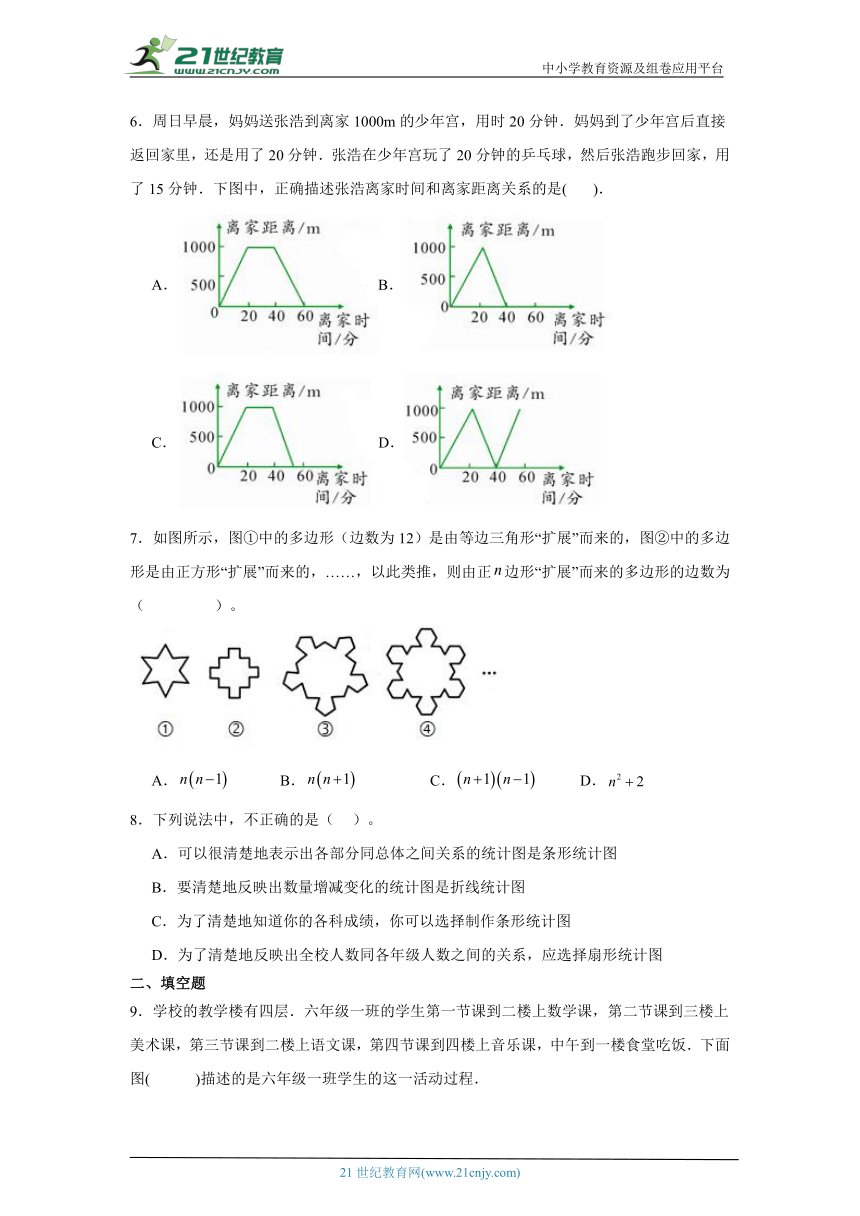
1., , , ,…,这一列数中的第10个数应该是( )。
A. B. C. D.
2.一个数值转换器原理如图所示,若输入x的值是13,为奇数,则第一次输出的结果是16,第二次输出的结果是8,……则第2015次输出的结果是( )。21*cnjy*com
A.1 B.2 C.4 D.8
3.一串数:2、3、6、11、18…是按某种规律排列的,这串数左起第112个是( )。
A.10100 B.12321 C.12323 D.1321
4.一组图形有规律的排列着。○△□☆○△□☆○△□☆○△□☆…第79个是( )。
A.○ B.△ C.□ D.☆
5.“龟兔赛跑”是我们非常熟悉的故事。兔子跑得快,但太骄傲,在途中睡了一觉。 乌龟跑得慢,但一直不停地跑。结果乌龟先抵达终点,赢得胜利。下图中,( )基本反映了该比赛的过程。
A. B.
C. D.
6.周日早晨,妈妈送张浩到离家1000m的少年宫,用时20分钟.妈妈到了少年宫后直接返回家里,还是用了20分钟.张浩在少年宫玩了20分钟的乒乓球,然后张浩跑步回家,用了15分钟.下图中,正确描述张浩离家时间和离家距离关系的是( ).
A.B.
C.D.
7.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,……,以此类推,则由正边形“扩展”而来的多边形的边数为( )。
A. B. C. D.
8.下列说法中,不正确的是( )。
A.可以很清楚地表示出各部分同总体之间关系的统计图是条形统计图
B.要清楚地反映出数量增减变化的统计图是折线统计图
C.为了清楚地知道你的各科成绩,你可以选择制作条形统计图
D.为了清楚地反映出全校人数同各年级人数之间的关系,应选择扇形统计图
二、填空题
9.学校的教学楼有四层.六年级一班的学生第一节课到二楼上数学课,第二节课到三楼上美术课,第三节课到二楼上语文课,第四节课到四楼上音乐课,中午到一楼食堂吃饭.下面图( )描述的是六年级一班学生的这一活动过程.
10.学校开展课外体育活动,下面是两位同学对参加各类运动的情况统计,请认真进行对比,进行相关计算,把统计表填写完整。
项目 足球 篮球 乒乓球 其他
人数 100 ( ) ( ) ( )
11.按规律填数。
2、7、12、17、( )。
2、8、32、128、( )。
12.用小棒按如图所示方式摆图形:摆50个八边形需要( )小棒,771根小棒可以摆( )个这样的八边形。
13.有5个黑色和白色棋子围成一圈,规定:将同色且相邻的两个棋子之间放入一个白色棋子,在异色且相邻的两个棋子之间放入一个黑色棋子,然后将原来的5个棋子拿掉.如果第一幅图的初始状态开始依照上述规定操作下去,对于圆圈上呈现5个棋子的情况,圆圈上黑子最多能有 个.
14.如图,用完全一样的小棒拼四边形,按这样的方法摆下去,第5个图形需要( )根小棒,第n(n是大于0的自然数)个图形需要( )根小棒。
三、判断题
15.。( )
16.1除以111的商的小数部分第15位数字是0。 ( )
17.按规律往下画,第19个图形是。( )
四、解答题
18.观察下图,想一想。
(1)依次排下去,第7幅图有多少个棋子?第15幅图呢?
(2)第n幅图有多少个棋子?
19.在一个圆周上有10个点,以这些点为端点或顶点,可以画出多少不同的(1)直线段(2)三角形(3)四边形?21·cn·jy·com
20.已知一列数按294736294736294……排列,那么前40个数字之和是多少?
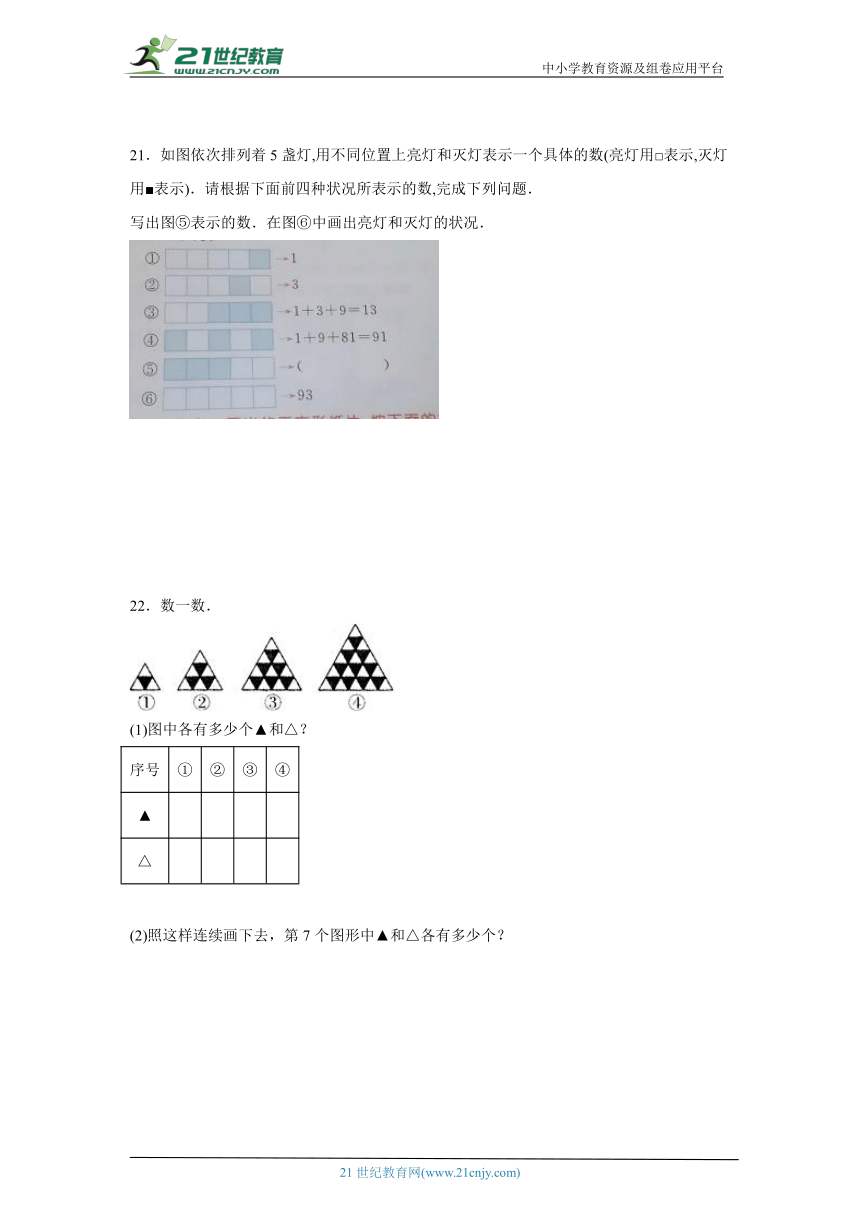
21.如图依次排列着5盏灯,用不同位置上亮灯和灭灯表示一个具体的数(亮灯用□表示,灭灯用■表示).请根据下面前四种状况所表示的数,完成下列问题.
写出图⑤表示的数.在图⑥中画出亮灯和灭灯的状况.
22.数一数.
(1)图中各有多少个▲和△?
序号 ① ② ③ ④
▲
△
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
参考答案:
1.B
【详解】从这列数中可以看出每一个数的分母就是这个数在这列数中的顺序×2,每一个数的分子就是分母-1。21教育网
故答案为:B
2.A
【分析】根据数值转换器依次求出前几次的输出的数值,再根据数值的变化,找出规律,然后利用规律进行求解。21cnjy.com
【详解】第1次输出的结果是16,
第2次输出的结果是8,
第3次输出的结果是×8=4,
第4次输出的结果是×4=2,
第5次输出的结果是×2=1,
第6次输出的结果是1+3=4,
第7次输出的结果是×4=2,
第8次输出的结果是×2=1,
……
所以,从第3次开始,每3次输出为一个循环组依次循环,
(2015-2)÷3=671,
所以,第2015次输出的结果是1。
故选:A
【点睛】本题考查了代数式求值,根据数值转换器求出从第3次开始,每3次输出为一个循环组依次循环是解题的关键。www.21-cn-jy.com
3.C
【分析】根据题意:从前面的几个数可以得出:相邻的两个数的差依次是1,3,5,7,……,所以得到第1个数:2;第2个数:2+1=3;第3个数:2+1+3=6;第4个数:2+1+3+5=11;第5个数:2+1+3+5+7=18;可得出第n个数:2+(n-1)2,题目中要求第112个数,即把n=112代入式子即可。【来源:21cnj*y.co*m】
【详解】第1个数:2;第2个数:2+1=3;第3个数:2+1+3=6;第4个数:2+1+3+5=11;第5个数:2+1+3+5+7=1821教育名师原创作品
2,3,6,11,18,……的差为1,3,5,7,……,可得当第n个数是:2+(n-1)2
当n=112时
2+(112-1)2
=2+111×111
=2+12321
=12323
故答案为:C。
【点睛】通过观察,分析,归纳并发现其中的规律,并应用发现的规律解决问题。
4.C
【分析】观察图形可知,这组图形的排列规律是:4个图形一个循环周期,分别按照○△□☆的顺序依次循环排列,据此求出第79个图形是第几个循环周期的第几个图形即可解答。
【详解】79÷4=19……3
所以第79个图形是第19循环周期的第3个图形是□;
故答案为:C。
【点睛】根据题干得出这组图形的排列规律是解决此类问题的关键。
5.B
【分析】根据题意可知:由于乌龟有耐心, -直往目的地奔跑,可知表示乌龟赛跑的图像应该是一条一直上升的直线,且比兔子早到达终点;由于兔子没有耐心,一开始表示兔子的赛跑的图像应该是一条上升的直线,到中途睡 了一觉,由于路程不改变,所以图像变为水平直线,睡了一觉起来再跑,图像又变为上升;据此分析B与C符合,由于兔子的速度比乌龟快,也就是开始时同一时间内兔子比乌龟跑的路程多,由此可得B符合,C不符合,据此解答。21世纪教育网版权所有
【详解】乌龟赛跑的图像应该是一条一直上升的直线,且比兔子早到达终点;兔子赛跑的图象应该是开始时是一条上升的直线,中途变为水平直线,然后又变为上升,且比乌龟晚到达终点;而且开始时,同一时间内兔子比乌龟跑的路程多,由此可得B符合。
故答案为:A。
【点睛】此题主要考查的是如何观察折线统计图并从图中获取信息。
6.C
【详解】略
7.B
【分析】由题意可知:等边三角形“扩展”而来的多边形的边数为12=3×(3+1),正方形“扩展”而来的多边形的边数为20=4×(4+1),正五边形“扩展”而来的多边形的边数为30=5×(5+1),正六边形“扩展”而来的多边形的边数为42=6×(6+1),…所以正n边形“扩展”而来的多边形的边数为n(n+1),据此解答即可。2·1·c·n·j·y
【详解】根据分析可知,正n边形“扩展”而来的多边形的边数为:n(n+1)。
故正确答案为:B
【点睛】本题主要考查了图形的变化规律,注意观察总结出规律,并能正确应用,解答此题的关键是判断出正n边形“扩展”而来的多边形的边数与n的关系。21·世纪*教育网
8.A
【分析】条形统计图能直观地表示出每个项目的具体数目;折线统计图能直观地反映事物变化情况;扇形统计图能直观地表示出各部分在总体中所占的百分比。
【详解】可以很清楚地表示出各部分同总体之间关系的统计图是扇形统计图,而不是条形统计图。
故答案为:A。
【点睛】明确各种统计图的特点是解答本题的关键。
9.③
【解析】略
10. 200 50 150
【分析】根据足球的数量和所占的百分率求出参加各类运动的总数量:100÷20%=500人,然后再根据“求一个数的百分之几是多少,用乘法计算”求出参加各类运动的数量,据此解答。
【详解】100÷20%=500(人)
参加篮球的人数:500×40%=200(人)
参加其他运动的人数:500×30%=150(人)
参加乒乓球的人数:500-200-150-100=50(人)
【点睛】本题关键是读懂图,找出单位“1”,然后根据它们各占总数量的百分之几进行求解。
11. 22 512
【分析】(1)观察给出的数列知道:奇数项上的数是它前面的奇数项上的数加10所得,偶数项上的数是它前面的偶数项上的数加10所得,由此得出答案;www-2-1-cnjy-com
(2)根据题干可知,第一个数乘4得第二个数,第三个数乘4得第四个数,依此乘4。
【详解】由分析得,
2、7、12、17、22。
2、8、32、128、512。
【点睛】此题考查的是找规律,解答此题关键是根据给出的数列中数与数的关系,找出其变化的规律,再由规律解决问题。21*cnjy*com
12. 351根 110
【分析】根据题图,可知一个八边形需要8根小棒,此后每增加一个八边形就增加7根小棒,以此类推,当有n个八边形时,需要8+7(n-1)=7n+1根小棒,据此解答即可。
【详解】当有n个八边形时,需要(7n+1)根小棒;
摆50个八边形时:
7×50+1
=350+1
=351(根);
当有771根小棒时:
7n+1=771
7n=770
n=110
【点睛】解答本题的关键是根据题图找到规律,再根据规律解决实际问题。
13.4个
【详解】5个棋子2种颜色,至少有2个相同颜色的棋子相邻,所以无论操作多少次,5个棋子中至少有1个是白子,所以黑子最多有4个。实际操作得到:所以最多有4个。
14. 16 3n+1
【分析】根据观察可知:第一个平行四边形需要4根小棒以后每增加一个平行四边形,增加3根小棒,则小棒的根数与摆成第几个平行四边形的规律是4+(n-1)×3=3n+1,据此解答。【版权所有:21教育】
【详解】第1个图形需要小棒:4根
第2个图形需要小棒:(根)
第3个图形需要小棒:(根)
第5个图形需要小棒:
4+(5-1)×3
=4+4×3
=4+12
=16(根)
第n个图形需要小棒:4+(n-1)×3=(3n+1)根。
第5个图形需要16根小棒,第n(n是大于0的自然数)个图形需要(3n+1)根小棒。
【点睛】本题考查数与形问题,找出小棒根数与平行四边形个数之间的关系是解题的关键。
15.√
【分析】从1开始的连续奇数相加,和等于奇数个数的平方,据此解答即可。
【详解】
故答案为:√。
【点睛】本题考查数与形,解答本题的关键是掌握题中相加数字的和的规律。
16.×
【详解】1÷111=0.009009…,循环节是009,三位,15÷3=5,所以商的小数部分第15位数字是9。【出处:21教育名师】
故答案为:×。
17.√
【分析】观察这组图形可得3个图形是一个周期,求第n个图形是什么,则用n÷3,得出的余数是1时则与第一个图形相同;得出的余数是2时则与第二个图形相同;没有余数时即与第三个图形相同。
【详解】19÷3=6……1,
所以第19个图形与第一个图形相同,是,即正确。
故答案为:√
【点睛】此题考查是的找规律,正确找出规律并用规律解决问题是解题关键。
18.(1)49个;225个(2)(n2)个
【分析】观察棋子的数目与图的序数之间的关系,发现:第1幅图:1=12个棋子;第2幅图:1+3=4=22个棋子;第3幅图:1+3+5=9=32个棋子;第4幅图:1+3+5+7=16=42个棋子,……,据此总结出一般规律,解答即可。【来源:21·世纪·教育·网】
【详解】第1幅图:1=12个棋子
第2幅图:1+3=4=22个棋子
第3幅图:1+3+5=9=32个棋子
第4幅图:1+3+5+7=16=42个棋子
……
所以第7幅图有72=49个棋子
第15幅图有152=225个棋子
第n幅图:(n2)个棋子
【点睛】本题考查数与形,解答本题的关键是找到棋子的数目与图的序数之间的关系。
19.线段:45条 三角形:120个 四边形:210个
【分析】首先观察是组合问题还是排列问题,那就要看你取的点是否与顺序有关?
很明显,你要画的三个图形都与取出点的顺序无关,所以三个问题都应该是组合问题。由于10个点都在圆周上,因此任意三点都不共线,故只要在10个点中任取2点,就可画出一条线段;在10个点中任取3个点,就可画出一个三角形;在10个点中任取4个点就可画出一个四边形。
【详解】(1),可画出45条线段;
(2),可画120个三角形;
(3),画210个四边形。
答:可以画出45条线段,120个三角形,210个四边形。
【点睛】本题的关键是在掌握线段、三角形、四边形的特征的基础上,合理的运用排列组合,选出合适的情况。
20.208
【分析】294736294736294……这一列数字是按照2、9、4、7、3、6这6个数字为一组进行循环出现的,求出40里面有多少个这样的一组,还余几;求出每组和,进而求出前40个数字的和。
【详解】2、9、4、7、3、6这6个数字为一组进行循环出现
2+9+4+7+3+6=31
40÷6=6(组)…4(个)
6组还余4个数字,余下的4个是2,9,4,7
2+9+4+7=22
31×6+22=208
答:前40个数字之和是208。
【点睛】解决这类问题往往是把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解。
21.由前四幅图可知:当灯灭时(■):从右边向左,第一个灯表示1;第二个灯表示3;第三个灯表示9;第五个灯表示81;1×3=3,3×3=9,后一个数是前一个的3倍,那么第四个灯表示9×3=27;当灯亮时□所表示的数不显示.那么,⑤中灭的灯是从右边数的第三、四、五这三个,就表示9+27+81=117.2-1-c-n-j-y
⑥93=81+9+3,应是从右边数的第二、三、五这三个灯熄灭:
【详解】略
22.(1)1,3,6,10
3,6,10,15
(2)▲有28个,△有36个
【详解】(1)填表如下:
序号 ① ② ③ ④
▲ 1 3 6 10
△ 3 6 10 15
(2)1+2+3+4+…+7=28(个)
1+2+3+4+…+8=36(个)
答:第7个图形中▲有28个,△有36个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第八单元数学广角——数与形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1., , , ,…,这一列数中的第10个数应该是( )。
A. B. C. D.
2.一个数值转换器原理如图所示,若输入x的值是13,为奇数,则第一次输出的结果是16,第二次输出的结果是8,……则第2015次输出的结果是( )。21*cnjy*com
A.1 B.2 C.4 D.8
3.一串数:2、3、6、11、18…是按某种规律排列的,这串数左起第112个是( )。
A.10100 B.12321 C.12323 D.1321
4.一组图形有规律的排列着。○△□☆○△□☆○△□☆○△□☆…第79个是( )。
A.○ B.△ C.□ D.☆
5.“龟兔赛跑”是我们非常熟悉的故事。兔子跑得快,但太骄傲,在途中睡了一觉。 乌龟跑得慢,但一直不停地跑。结果乌龟先抵达终点,赢得胜利。下图中,( )基本反映了该比赛的过程。
A. B.
C. D.
6.周日早晨,妈妈送张浩到离家1000m的少年宫,用时20分钟.妈妈到了少年宫后直接返回家里,还是用了20分钟.张浩在少年宫玩了20分钟的乒乓球,然后张浩跑步回家,用了15分钟.下图中,正确描述张浩离家时间和离家距离关系的是( ).
A.B.
C.D.
7.如图所示,图①中的多边形(边数为12)是由等边三角形“扩展”而来的,图②中的多边形是由正方形“扩展”而来的,……,以此类推,则由正边形“扩展”而来的多边形的边数为( )。
A. B. C. D.
8.下列说法中,不正确的是( )。
A.可以很清楚地表示出各部分同总体之间关系的统计图是条形统计图
B.要清楚地反映出数量增减变化的统计图是折线统计图
C.为了清楚地知道你的各科成绩,你可以选择制作条形统计图
D.为了清楚地反映出全校人数同各年级人数之间的关系,应选择扇形统计图
二、填空题
9.学校的教学楼有四层.六年级一班的学生第一节课到二楼上数学课,第二节课到三楼上美术课,第三节课到二楼上语文课,第四节课到四楼上音乐课,中午到一楼食堂吃饭.下面图( )描述的是六年级一班学生的这一活动过程.
10.学校开展课外体育活动,下面是两位同学对参加各类运动的情况统计,请认真进行对比,进行相关计算,把统计表填写完整。
项目 足球 篮球 乒乓球 其他
人数 100 ( ) ( ) ( )
11.按规律填数。
2、7、12、17、( )。
2、8、32、128、( )。
12.用小棒按如图所示方式摆图形:摆50个八边形需要( )小棒,771根小棒可以摆( )个这样的八边形。
13.有5个黑色和白色棋子围成一圈,规定:将同色且相邻的两个棋子之间放入一个白色棋子,在异色且相邻的两个棋子之间放入一个黑色棋子,然后将原来的5个棋子拿掉.如果第一幅图的初始状态开始依照上述规定操作下去,对于圆圈上呈现5个棋子的情况,圆圈上黑子最多能有 个.
14.如图,用完全一样的小棒拼四边形,按这样的方法摆下去,第5个图形需要( )根小棒,第n(n是大于0的自然数)个图形需要( )根小棒。
三、判断题
15.。( )
16.1除以111的商的小数部分第15位数字是0。 ( )
17.按规律往下画,第19个图形是。( )
四、解答题
18.观察下图,想一想。
(1)依次排下去,第7幅图有多少个棋子?第15幅图呢?
(2)第n幅图有多少个棋子?
19.在一个圆周上有10个点,以这些点为端点或顶点,可以画出多少不同的(1)直线段(2)三角形(3)四边形?21·cn·jy·com
20.已知一列数按294736294736294……排列,那么前40个数字之和是多少?
21.如图依次排列着5盏灯,用不同位置上亮灯和灭灯表示一个具体的数(亮灯用□表示,灭灯用■表示).请根据下面前四种状况所表示的数,完成下列问题.
写出图⑤表示的数.在图⑥中画出亮灯和灭灯的状况.
22.数一数.
(1)图中各有多少个▲和△?
序号 ① ② ③ ④
▲
△
(2)照这样连续画下去,第7个图形中▲和△各有多少个?
参考答案:
1.B
【详解】从这列数中可以看出每一个数的分母就是这个数在这列数中的顺序×2,每一个数的分子就是分母-1。21教育网
故答案为:B
2.A
【分析】根据数值转换器依次求出前几次的输出的数值,再根据数值的变化,找出规律,然后利用规律进行求解。21cnjy.com
【详解】第1次输出的结果是16,
第2次输出的结果是8,
第3次输出的结果是×8=4,
第4次输出的结果是×4=2,
第5次输出的结果是×2=1,
第6次输出的结果是1+3=4,
第7次输出的结果是×4=2,
第8次输出的结果是×2=1,
……
所以,从第3次开始,每3次输出为一个循环组依次循环,
(2015-2)÷3=671,
所以,第2015次输出的结果是1。
故选:A
【点睛】本题考查了代数式求值,根据数值转换器求出从第3次开始,每3次输出为一个循环组依次循环是解题的关键。www.21-cn-jy.com
3.C
【分析】根据题意:从前面的几个数可以得出:相邻的两个数的差依次是1,3,5,7,……,所以得到第1个数:2;第2个数:2+1=3;第3个数:2+1+3=6;第4个数:2+1+3+5=11;第5个数:2+1+3+5+7=18;可得出第n个数:2+(n-1)2,题目中要求第112个数,即把n=112代入式子即可。【来源:21cnj*y.co*m】
【详解】第1个数:2;第2个数:2+1=3;第3个数:2+1+3=6;第4个数:2+1+3+5=11;第5个数:2+1+3+5+7=1821教育名师原创作品
2,3,6,11,18,……的差为1,3,5,7,……,可得当第n个数是:2+(n-1)2
当n=112时
2+(112-1)2
=2+111×111
=2+12321
=12323
故答案为:C。
【点睛】通过观察,分析,归纳并发现其中的规律,并应用发现的规律解决问题。
4.C
【分析】观察图形可知,这组图形的排列规律是:4个图形一个循环周期,分别按照○△□☆的顺序依次循环排列,据此求出第79个图形是第几个循环周期的第几个图形即可解答。
【详解】79÷4=19……3
所以第79个图形是第19循环周期的第3个图形是□;
故答案为:C。
【点睛】根据题干得出这组图形的排列规律是解决此类问题的关键。
5.B
【分析】根据题意可知:由于乌龟有耐心, -直往目的地奔跑,可知表示乌龟赛跑的图像应该是一条一直上升的直线,且比兔子早到达终点;由于兔子没有耐心,一开始表示兔子的赛跑的图像应该是一条上升的直线,到中途睡 了一觉,由于路程不改变,所以图像变为水平直线,睡了一觉起来再跑,图像又变为上升;据此分析B与C符合,由于兔子的速度比乌龟快,也就是开始时同一时间内兔子比乌龟跑的路程多,由此可得B符合,C不符合,据此解答。21世纪教育网版权所有
【详解】乌龟赛跑的图像应该是一条一直上升的直线,且比兔子早到达终点;兔子赛跑的图象应该是开始时是一条上升的直线,中途变为水平直线,然后又变为上升,且比乌龟晚到达终点;而且开始时,同一时间内兔子比乌龟跑的路程多,由此可得B符合。
故答案为:A。
【点睛】此题主要考查的是如何观察折线统计图并从图中获取信息。
6.C
【详解】略
7.B
【分析】由题意可知:等边三角形“扩展”而来的多边形的边数为12=3×(3+1),正方形“扩展”而来的多边形的边数为20=4×(4+1),正五边形“扩展”而来的多边形的边数为30=5×(5+1),正六边形“扩展”而来的多边形的边数为42=6×(6+1),…所以正n边形“扩展”而来的多边形的边数为n(n+1),据此解答即可。2·1·c·n·j·y
【详解】根据分析可知,正n边形“扩展”而来的多边形的边数为:n(n+1)。
故正确答案为:B
【点睛】本题主要考查了图形的变化规律,注意观察总结出规律,并能正确应用,解答此题的关键是判断出正n边形“扩展”而来的多边形的边数与n的关系。21·世纪*教育网
8.A
【分析】条形统计图能直观地表示出每个项目的具体数目;折线统计图能直观地反映事物变化情况;扇形统计图能直观地表示出各部分在总体中所占的百分比。
【详解】可以很清楚地表示出各部分同总体之间关系的统计图是扇形统计图,而不是条形统计图。
故答案为:A。
【点睛】明确各种统计图的特点是解答本题的关键。
9.③
【解析】略
10. 200 50 150
【分析】根据足球的数量和所占的百分率求出参加各类运动的总数量:100÷20%=500人,然后再根据“求一个数的百分之几是多少,用乘法计算”求出参加各类运动的数量,据此解答。
【详解】100÷20%=500(人)
参加篮球的人数:500×40%=200(人)
参加其他运动的人数:500×30%=150(人)
参加乒乓球的人数:500-200-150-100=50(人)
【点睛】本题关键是读懂图,找出单位“1”,然后根据它们各占总数量的百分之几进行求解。
11. 22 512
【分析】(1)观察给出的数列知道:奇数项上的数是它前面的奇数项上的数加10所得,偶数项上的数是它前面的偶数项上的数加10所得,由此得出答案;www-2-1-cnjy-com
(2)根据题干可知,第一个数乘4得第二个数,第三个数乘4得第四个数,依此乘4。
【详解】由分析得,
2、7、12、17、22。
2、8、32、128、512。
【点睛】此题考查的是找规律,解答此题关键是根据给出的数列中数与数的关系,找出其变化的规律,再由规律解决问题。21*cnjy*com
12. 351根 110
【分析】根据题图,可知一个八边形需要8根小棒,此后每增加一个八边形就增加7根小棒,以此类推,当有n个八边形时,需要8+7(n-1)=7n+1根小棒,据此解答即可。
【详解】当有n个八边形时,需要(7n+1)根小棒;
摆50个八边形时:
7×50+1
=350+1
=351(根);
当有771根小棒时:
7n+1=771
7n=770
n=110
【点睛】解答本题的关键是根据题图找到规律,再根据规律解决实际问题。
13.4个
【详解】5个棋子2种颜色,至少有2个相同颜色的棋子相邻,所以无论操作多少次,5个棋子中至少有1个是白子,所以黑子最多有4个。实际操作得到:所以最多有4个。
14. 16 3n+1
【分析】根据观察可知:第一个平行四边形需要4根小棒以后每增加一个平行四边形,增加3根小棒,则小棒的根数与摆成第几个平行四边形的规律是4+(n-1)×3=3n+1,据此解答。【版权所有:21教育】
【详解】第1个图形需要小棒:4根
第2个图形需要小棒:(根)
第3个图形需要小棒:(根)
第5个图形需要小棒:
4+(5-1)×3
=4+4×3
=4+12
=16(根)
第n个图形需要小棒:4+(n-1)×3=(3n+1)根。
第5个图形需要16根小棒,第n(n是大于0的自然数)个图形需要(3n+1)根小棒。
【点睛】本题考查数与形问题,找出小棒根数与平行四边形个数之间的关系是解题的关键。
15.√
【分析】从1开始的连续奇数相加,和等于奇数个数的平方,据此解答即可。
【详解】
故答案为:√。
【点睛】本题考查数与形,解答本题的关键是掌握题中相加数字的和的规律。
16.×
【详解】1÷111=0.009009…,循环节是009,三位,15÷3=5,所以商的小数部分第15位数字是9。【出处:21教育名师】
故答案为:×。
17.√
【分析】观察这组图形可得3个图形是一个周期,求第n个图形是什么,则用n÷3,得出的余数是1时则与第一个图形相同;得出的余数是2时则与第二个图形相同;没有余数时即与第三个图形相同。
【详解】19÷3=6……1,
所以第19个图形与第一个图形相同,是,即正确。
故答案为:√
【点睛】此题考查是的找规律,正确找出规律并用规律解决问题是解题关键。
18.(1)49个;225个(2)(n2)个
【分析】观察棋子的数目与图的序数之间的关系,发现:第1幅图:1=12个棋子;第2幅图:1+3=4=22个棋子;第3幅图:1+3+5=9=32个棋子;第4幅图:1+3+5+7=16=42个棋子,……,据此总结出一般规律,解答即可。【来源:21·世纪·教育·网】
【详解】第1幅图:1=12个棋子
第2幅图:1+3=4=22个棋子
第3幅图:1+3+5=9=32个棋子
第4幅图:1+3+5+7=16=42个棋子
……
所以第7幅图有72=49个棋子
第15幅图有152=225个棋子
第n幅图:(n2)个棋子
【点睛】本题考查数与形,解答本题的关键是找到棋子的数目与图的序数之间的关系。
19.线段:45条 三角形:120个 四边形:210个
【分析】首先观察是组合问题还是排列问题,那就要看你取的点是否与顺序有关?
很明显,你要画的三个图形都与取出点的顺序无关,所以三个问题都应该是组合问题。由于10个点都在圆周上,因此任意三点都不共线,故只要在10个点中任取2点,就可画出一条线段;在10个点中任取3个点,就可画出一个三角形;在10个点中任取4个点就可画出一个四边形。
【详解】(1),可画出45条线段;
(2),可画120个三角形;
(3),画210个四边形。
答:可以画出45条线段,120个三角形,210个四边形。
【点睛】本题的关键是在掌握线段、三角形、四边形的特征的基础上,合理的运用排列组合,选出合适的情况。
20.208
【分析】294736294736294……这一列数字是按照2、9、4、7、3、6这6个数字为一组进行循环出现的,求出40里面有多少个这样的一组,还余几;求出每组和,进而求出前40个数字的和。
【详解】2、9、4、7、3、6这6个数字为一组进行循环出现
2+9+4+7+3+6=31
40÷6=6(组)…4(个)
6组还余4个数字,余下的4个是2,9,4,7
2+9+4+7=22
31×6+22=208
答:前40个数字之和是208。
【点睛】解决这类问题往往是把重复出现的部分看成一组,先找出排列的周期性规律,再根据规律求解。
21.由前四幅图可知:当灯灭时(■):从右边向左,第一个灯表示1;第二个灯表示3;第三个灯表示9;第五个灯表示81;1×3=3,3×3=9,后一个数是前一个的3倍,那么第四个灯表示9×3=27;当灯亮时□所表示的数不显示.那么,⑤中灭的灯是从右边数的第三、四、五这三个,就表示9+27+81=117.2-1-c-n-j-y
⑥93=81+9+3,应是从右边数的第二、三、五这三个灯熄灭:
【详解】略
22.(1)1,3,6,10
3,6,10,15
(2)▲有28个,△有36个
【详解】(1)填表如下:
序号 ① ② ③ ④
▲ 1 3 6 10
△ 3 6 10 15
(2)1+2+3+4+…+7=28(个)
1+2+3+4+…+8=36(个)
答:第7个图形中▲有28个,△有36个.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
