北师大版七年级下册 1.4 整式的乘法 课件(23张PPT)
文档属性
| 名称 | 北师大版七年级下册 1.4 整式的乘法 课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 751.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-27 00:00:00 | ||
图片预览


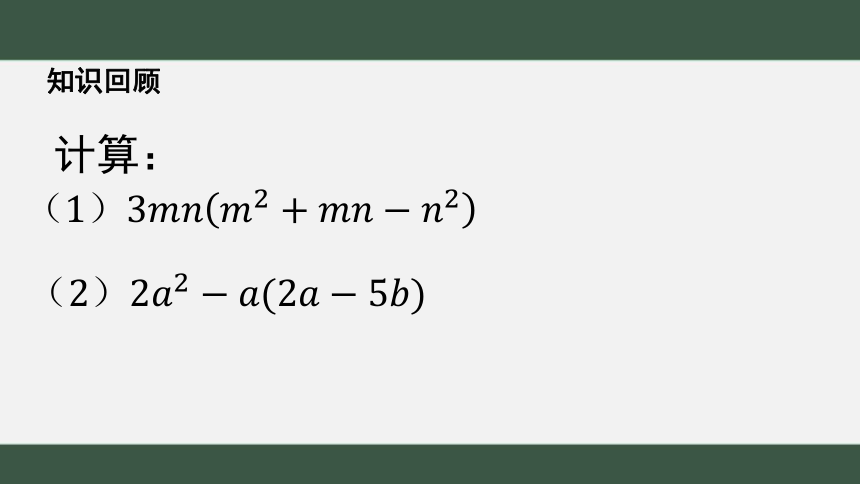




文档简介
(共23张PPT)
1.4 整式的乘法
知识回顾
单项式乘法的法则:
单项式与多项式相乘的法则:
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式。
单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加。
计算:
(2)
知识回顾
3mn· ·
= ·
=
= 5
温馨提示:
1.相乘时要带上每一项的符号
2.展开式中有同类项要合并
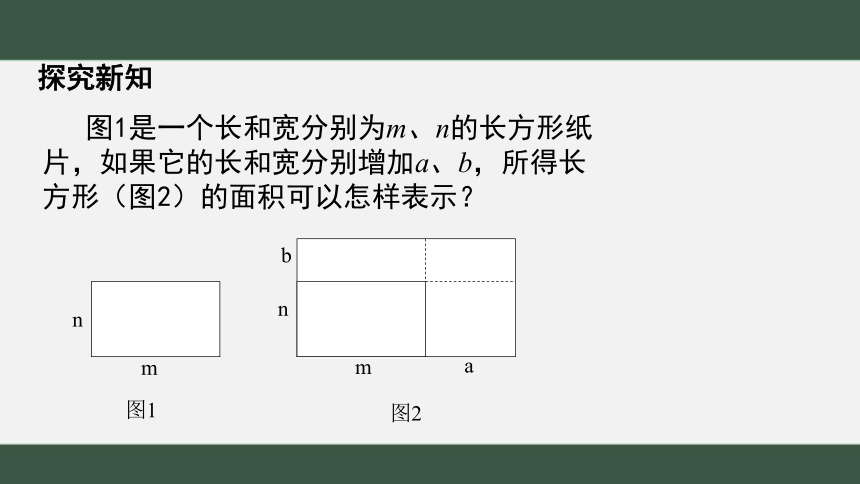
探究新知
图1是一个长和宽分别为m、n的长方形纸片,如果它的长和宽分别增加a、b,所得长方形(图2)的面积可以怎样表示?
m
m
n
a
b
n
图1
图2
方法一:所得长方形的长为(m+a),
宽为(n+b),所以面积可以表示为:
n+b
m
n
b
m+a
m
n
b
方法二:所得长方形可以看做是由上下两个长方形组成的,上面的长方形面积为b(m+a),下面的长方形面积为n(m+a),这样长方形的面积就可以表示为
b(m+a)+ n(m+a)
方法三:所得长方形可以看做是由左右两个长方形组成的,左边的长方形面积为m(b+n),右边的长方形面积为
a(b+n),这样长方形的面积就可以表示为
m(b+n)+ a(b+n)
b(m+a)
n(m+a)
a(b+n)
m(b+n)
m
n
b
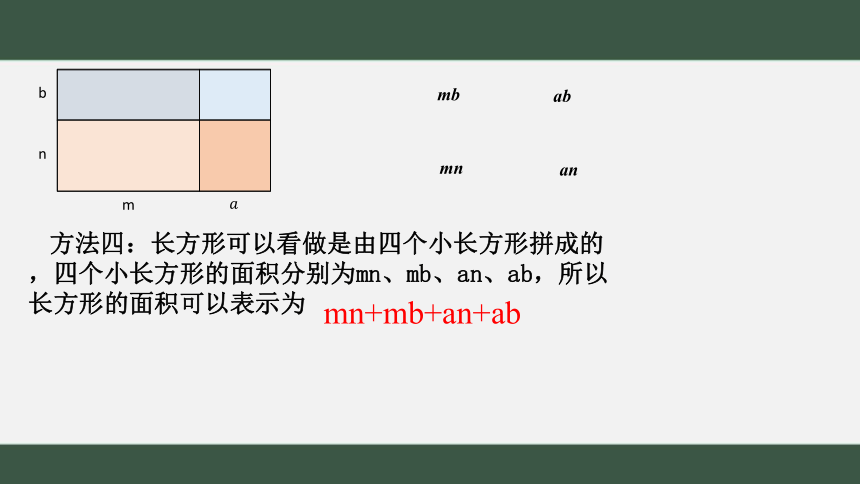
方法四:长方形可以看做是由四个小长方形拼成的,四个小长方形的面积分别为mn、mb、an、ab,所以长方形的面积可以表示为
ab
an
mn
mb
mn+mb+an+ab
方法三
方法二
(a+m)(b+n)
=a(b+n)+m(b+n)
=ab+an+bm+mn
(a+m)(b+n)
= b(a+m)+n(a+m)
=ab+bm+an+mn
或
探究尝试
1、你能说出
这一步运算的道理吗?
同理可得:
=
=
转化思想
总结归纳
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加。
(m+a)(n+b)=mn+mb +an+ab
如何进行多项式与多项式相乘的运算?
结合这个算式
例1 计算:
典型例题
(1)
(2)
(3)
例题解析
1·+·
0.6 0.6 +
0.6 1.6 +
=····
=
=
题后思:
1.不要漏乘;
2.相乘时一定要带上每一项符号;
3.展开式中有同类项要合并.
小试牛刀
(1)(m+2n)(m 2n)
(2)(x+2y)2
(3)
(1) (m+2n)(m 2n)
=
=
= (x+2y) (x+2y)
= xy xy +4
= xy +4
(2)(
解析
= m· m m·2n+2n·m 2n·2n
= x· x+ x· 2y + 2y ·x+ 2y · 2y
(3)
=-2m·3m 2m·2 3m
= -6 4m m 1
=-6 m 1
变式训练
解析
= · +·+·1 1 · ·
= + +
=
=+3+2+6 +2
=+3+2+6 2
=5++8
温馨提示:
1、注意运算顺序
2、减号后面的整体要加括号
不要漏乘
加括号
原式=(2x2-x+2x-1)-(x-3)(x-3)
=2x2-x+2x-1-(x2 -3x -3x+9)
=2x2-x+2x-1-x2+6x-9
=x2+7x-10.
当x=-2时,
原式=(-2)2+7×(-2)-10=-20.
及时巩固
1.先化简,再求值:
(x+1)(2x-1)-(x-3)2,其中x=-2.
解析
解析: (a-2)(b-2)
=ab-2a-2b+4
=ab-2(a+b)+4
=2-2×3+4
=0.
拓展提高
1、已知a+b=3,ab=2,则代数式(a-2)(b-2)的值是__.
0
a
b
a-2b
a-b
2.某校有一块边长为a的正方形花圃,它有两横一纵宽度均为b的3条人行道把花圃分隔成6块,该花圃的实际种花面积是多少?
解:该花圃的实际种花面积是(a-b)(a-2b)=a2-3ab+2b2.
拓展提高
收获感悟
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加。
(m+a)(n+b)=mn+mb+an+ab
温馨提示:
1、不要漏乘;
2、相乘时一定要带上每一项符号;
3、展开式中有同类项要合并.
同学们,再见!
1.4 整式的乘法
知识回顾
单项式乘法的法则:
单项式与多项式相乘的法则:
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余字母连同它的指数不变,作为积的因式。
单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加。
计算:
(2)
知识回顾
3mn· ·
= ·
=
= 5
温馨提示:
1.相乘时要带上每一项的符号
2.展开式中有同类项要合并
探究新知
图1是一个长和宽分别为m、n的长方形纸片,如果它的长和宽分别增加a、b,所得长方形(图2)的面积可以怎样表示?
m
m
n
a
b
n
图1
图2
方法一:所得长方形的长为(m+a),
宽为(n+b),所以面积可以表示为:
n+b
m
n
b
m+a
m
n
b
方法二:所得长方形可以看做是由上下两个长方形组成的,上面的长方形面积为b(m+a),下面的长方形面积为n(m+a),这样长方形的面积就可以表示为
b(m+a)+ n(m+a)
方法三:所得长方形可以看做是由左右两个长方形组成的,左边的长方形面积为m(b+n),右边的长方形面积为
a(b+n),这样长方形的面积就可以表示为
m(b+n)+ a(b+n)
b(m+a)
n(m+a)
a(b+n)
m(b+n)
m
n
b
方法四:长方形可以看做是由四个小长方形拼成的,四个小长方形的面积分别为mn、mb、an、ab,所以长方形的面积可以表示为
ab
an
mn
mb
mn+mb+an+ab
方法三
方法二
(a+m)(b+n)
=a(b+n)+m(b+n)
=ab+an+bm+mn
(a+m)(b+n)
= b(a+m)+n(a+m)
=ab+bm+an+mn
或
探究尝试
1、你能说出
这一步运算的道理吗?
同理可得:
=
=
转化思想
总结归纳
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加。
(m+a)(n+b)=mn+mb +an+ab
如何进行多项式与多项式相乘的运算?
结合这个算式
例1 计算:
典型例题
(1)
(2)
(3)
例题解析
1·+·
0.6 0.6 +
0.6 1.6 +
=····
=
=
题后思:
1.不要漏乘;
2.相乘时一定要带上每一项符号;
3.展开式中有同类项要合并.
小试牛刀
(1)(m+2n)(m 2n)
(2)(x+2y)2
(3)
(1) (m+2n)(m 2n)
=
=
= (x+2y) (x+2y)
= xy xy +4
= xy +4
(2)(
解析
= m· m m·2n+2n·m 2n·2n
= x· x+ x· 2y + 2y ·x+ 2y · 2y
(3)
=-2m·3m 2m·2 3m
= -6 4m m 1
=-6 m 1
变式训练
解析
= · +·+·1 1 · ·
= + +
=
=+3+2+6 +2
=+3+2+6 2
=5++8
温馨提示:
1、注意运算顺序
2、减号后面的整体要加括号
不要漏乘
加括号
原式=(2x2-x+2x-1)-(x-3)(x-3)
=2x2-x+2x-1-(x2 -3x -3x+9)
=2x2-x+2x-1-x2+6x-9
=x2+7x-10.
当x=-2时,
原式=(-2)2+7×(-2)-10=-20.
及时巩固
1.先化简,再求值:
(x+1)(2x-1)-(x-3)2,其中x=-2.
解析
解析: (a-2)(b-2)
=ab-2a-2b+4
=ab-2(a+b)+4
=2-2×3+4
=0.
拓展提高
1、已知a+b=3,ab=2,则代数式(a-2)(b-2)的值是__.
0
a
b
a-2b
a-b
2.某校有一块边长为a的正方形花圃,它有两横一纵宽度均为b的3条人行道把花圃分隔成6块,该花圃的实际种花面积是多少?
解:该花圃的实际种花面积是(a-b)(a-2b)=a2-3ab+2b2.
拓展提高
收获感悟
多项式与多项式相乘的法则:
多项式与多项式相乘,先用一个多项式的每一项去乘另一个多项式的每一项,再把所得的积相加。
(m+a)(n+b)=mn+mb+an+ab
温馨提示:
1、不要漏乘;
2、相乘时一定要带上每一项符号;
3、展开式中有同类项要合并.
同学们,再见!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
