北师大版七年级下册 1.5 平方差公式的应用 课件(共16张PPT)
文档属性
| 名称 | 北师大版七年级下册 1.5 平方差公式的应用 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 457.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-27 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
平方差公式的应用
导入新课
( a + b )( a b ) = a 2 b 2 两数和与这两数差的积,等于它们的平方差
1.问:请用符号语言和文字语言表示平方差公式
2.利用平方差公式计算:
(1)(2 x + 7 b )(2 x – 7 b );
A.2x2-7b2 B.4x2-9b2 C.4x2+49b2
( 2 )(- m + 3 n )( m + 3 n ) .
A.-m2+3n2 B.m2-9n2 C.9n2-m2
3.平方差公式中的字母可以表示什么?
公式中a、b可以表示 数 或 代数式
B
C
新课讲授
b
b
a2-b2
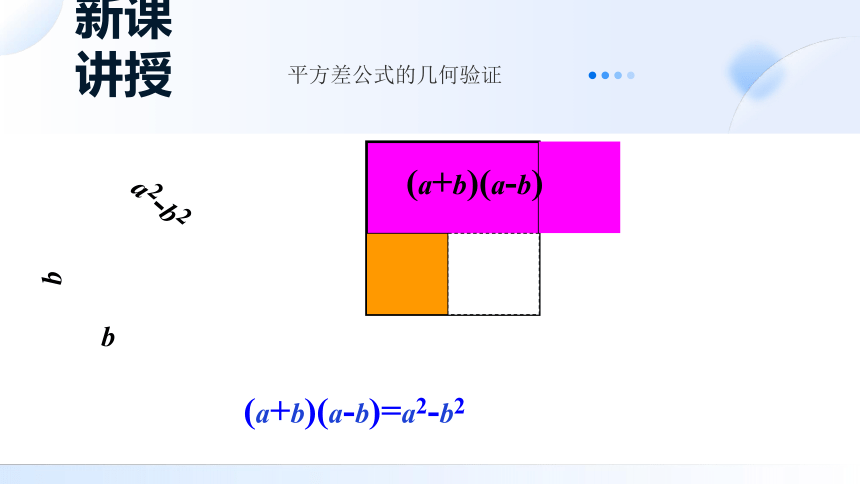
(a+b)(a-b)
(a+b)(a-b)=a2-b2
平方差公式的几何验证
公元 3 世纪中国古代数学家赵爽的“面积割补法”来证明平方差公式。赵爽在注释《周髀算经》中的“勾股圆方图”时说: “勾实之矩以股弦差为广,股弦并为袤,而股实方其里。……股实之矩以勾弦差为广,勾弦并为袤,而勾实方其里。” 对赵爽的生平人们知之甚少,在《〈周髀算经〉注》的前言里,赵爽说自己“负薪余日,聊观《周髀》”,意思是说,在打柴的空余时间里,钻研古代天文学著作《周髀算经》。迫于生计辛苦劳作,却不忘做学问,古人的勤奋感人至深。
数学小史
做一做:
你还有其他的证明方法吗?发挥你的聪明才智,动手操作一下吧!
步骤一:在边长为a的大正方形卡纸中,剪去一个边长为b的小正方形;
步骤二:再把剩余的图形剪开拼接成新的图形,用含a、b的代数式分别表示步骤一和步骤二中得到的图形的面积。
方案一
方案二
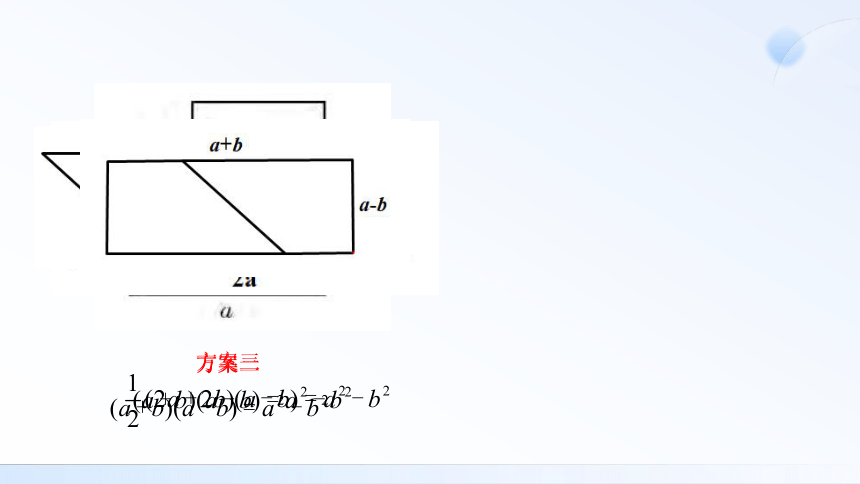
方案三
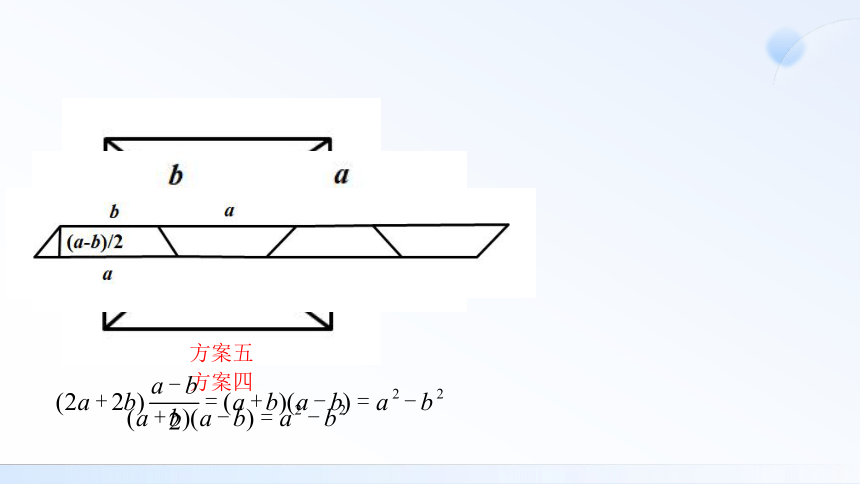
方案四
方案五
事实上,在我们国家的少数民族水族里,他们使用的鞋垫的纹理、马尾绣背带心、吃饭的桌子、服饰绣片纹理中都蕴含有平方差公式.
自主探究
7×9= 11×13= 79×81=
8×8= 12×12= 80×80=
(a+1)(a 1)=a2 12
(1)计算下列各式,并观察他们的共同特点:
(2)从以上的过程中,你发现了什么规律?请用字母表示这一规律?
63
143
144
6399
6400
64
两个连续奇数的积等于中间所夹偶数平方减1.
例1 计算:
(1) 103×97
解:
原式=(100+3)(100-3)
= 1002-32
=10000 – 9
=9991;
解:
原式=20162-(2016+1)(2016-1)
=20162-(20162-1)
=20162-20162+1=1;
注意:不能直接应用公式的,要经过变形才可以应用
(2)20162 -2017×2015
例2 计算:
(1)a2(a+b)(a-b)+a2b2
解:
原式= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y + 1.
解:
原式= a2(a2-b2)+a2b2
= a4-a2b2+a2b2
= a4.
(2) (y+2) (y-2) – (y-1) (y+5) .
1.(x-y)(x+y)(x2+y2);
解:
原式= (x2-y2)(x2+y2)
= x4 -y4
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
先化简,再求值:(a+b)(a-b)+b(a+2b)-b2,其中a=1,b=-2.
能力提升:
2.计算:(1)1007×993; (2)118×122.
当堂检测
拓展延伸:
3.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖的部分的面积是 (用含a,b的代数式表示).
课堂小结
“9对3说,我除了你,还是你;
4对2说,我除了2还是2;
1对0说,我除了你,一切都没有意义;
0对1说,我除了你,就是孤独的自己”。
我想数学是浪漫的,它比任何东西都完美,
因为它推理考证,真实严谨,从不说谎……
希望同学们
让数学“冰冷的美丽”焕发出“火热的思考”!
同学们,再见!
平方差公式的应用
导入新课
( a + b )( a b ) = a 2 b 2 两数和与这两数差的积,等于它们的平方差
1.问:请用符号语言和文字语言表示平方差公式
2.利用平方差公式计算:
(1)(2 x + 7 b )(2 x – 7 b );
A.2x2-7b2 B.4x2-9b2 C.4x2+49b2
( 2 )(- m + 3 n )( m + 3 n ) .
A.-m2+3n2 B.m2-9n2 C.9n2-m2
3.平方差公式中的字母可以表示什么?
公式中a、b可以表示 数 或 代数式
B
C
新课讲授
b
b
a2-b2
(a+b)(a-b)
(a+b)(a-b)=a2-b2
平方差公式的几何验证
公元 3 世纪中国古代数学家赵爽的“面积割补法”来证明平方差公式。赵爽在注释《周髀算经》中的“勾股圆方图”时说: “勾实之矩以股弦差为广,股弦并为袤,而股实方其里。……股实之矩以勾弦差为广,勾弦并为袤,而勾实方其里。” 对赵爽的生平人们知之甚少,在《〈周髀算经〉注》的前言里,赵爽说自己“负薪余日,聊观《周髀》”,意思是说,在打柴的空余时间里,钻研古代天文学著作《周髀算经》。迫于生计辛苦劳作,却不忘做学问,古人的勤奋感人至深。
数学小史
做一做:
你还有其他的证明方法吗?发挥你的聪明才智,动手操作一下吧!
步骤一:在边长为a的大正方形卡纸中,剪去一个边长为b的小正方形;
步骤二:再把剩余的图形剪开拼接成新的图形,用含a、b的代数式分别表示步骤一和步骤二中得到的图形的面积。
方案一
方案二
方案三
方案四
方案五
事实上,在我们国家的少数民族水族里,他们使用的鞋垫的纹理、马尾绣背带心、吃饭的桌子、服饰绣片纹理中都蕴含有平方差公式.
自主探究
7×9= 11×13= 79×81=
8×8= 12×12= 80×80=
(a+1)(a 1)=a2 12
(1)计算下列各式,并观察他们的共同特点:
(2)从以上的过程中,你发现了什么规律?请用字母表示这一规律?
63
143
144
6399
6400
64
两个连续奇数的积等于中间所夹偶数平方减1.
例1 计算:
(1) 103×97
解:
原式=(100+3)(100-3)
= 1002-32
=10000 – 9
=9991;
解:
原式=20162-(2016+1)(2016-1)
=20162-(20162-1)
=20162-20162+1=1;
注意:不能直接应用公式的,要经过变形才可以应用
(2)20162 -2017×2015
例2 计算:
(1)a2(a+b)(a-b)+a2b2
解:
原式= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= -4y + 1.
解:
原式= a2(a2-b2)+a2b2
= a4-a2b2+a2b2
= a4.
(2) (y+2) (y-2) – (y-1) (y+5) .
1.(x-y)(x+y)(x2+y2);
解:
原式= (x2-y2)(x2+y2)
= x4 -y4
2.若A=(2+1)(22+1)(24+1),则A的值是______.
解析:A=(2+1)(22+1)(24+1)
=[(2-1)(2+1)(22+1)(24+1)]÷(2-1)
=[(22-1)(22+1)(24+1)]÷(2-1)
=[(24-1)(24+1)]÷(2-1)
=(28-1)÷(2-1)
=28-1.
28-1
先化简,再求值:(a+b)(a-b)+b(a+2b)-b2,其中a=1,b=-2.
能力提升:
2.计算:(1)1007×993; (2)118×122.
当堂检测
拓展延伸:
3.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖的部分的面积是 (用含a,b的代数式表示).
课堂小结
“9对3说,我除了你,还是你;
4对2说,我除了2还是2;
1对0说,我除了你,一切都没有意义;
0对1说,我除了你,就是孤独的自己”。
我想数学是浪漫的,它比任何东西都完美,
因为它推理考证,真实严谨,从不说谎……
希望同学们
让数学“冰冷的美丽”焕发出“火热的思考”!
同学们,再见!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
