2.2方差与标准差课件(苏科版九年级上)
文档属性
| 名称 | 2.2方差与标准差课件(苏科版九年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 116.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-26 00:00:00 | ||
图片预览



文档简介
课件9张PPT。复习题:1.平均数、众数、中位数的意义?哪个应用最广泛?
2.求下列数据的平均数、众数和中位数
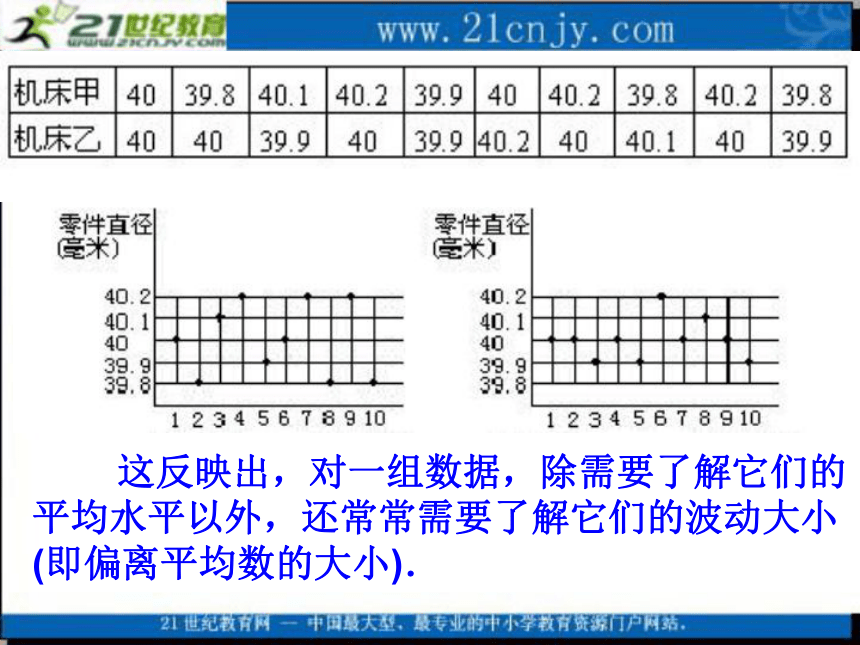
450,420,500,450,500,600,500,480,480,500。3.数据9,9,x,7的众数与平均数若恰好相等,则这组数据的中位数为_______. 引例 两台机床同时生产直径是40毫米的零件.为了检验产品质量,从产品中抽出10件进行测量,结果如下(单位:毫米):分别计算这两组数据的平均数 甲、乙两机床性能是否都一样好? 这反映出,对一组数据,除需要了解它们的平均水平以外,还常常需要了解它们的波动大小(即偏离平均数的大小). 描述一组数据的波动大小,可以采用不止一种办法.本课介绍“方差”即是一种方法. 2.2方差和标准差
来衡量这组数据的波动大小,并把它叫做这组数据的方差.一组数据方差越大,说明这组数据波动越大 请计算引例中机床甲、乙两组数据的方差 从0.026>0.008可以比较出,机床甲生产的10个零件直径比机床乙生产的10个零件直径波动要大 例1 已知两组数据:
分别计算这两组数据的方差. (1)求平均数 分析(2)求方差 (3)比较方差得出结论 用来衡量一组数据的波动的方法还可用一组
数据的标准差,即 公式④(即标准差)也是用来衡量一组数据波动
大小的重要的量.如
2.求下列数据的平均数、众数和中位数
450,420,500,450,500,600,500,480,480,500。3.数据9,9,x,7的众数与平均数若恰好相等,则这组数据的中位数为_______. 引例 两台机床同时生产直径是40毫米的零件.为了检验产品质量,从产品中抽出10件进行测量,结果如下(单位:毫米):分别计算这两组数据的平均数 甲、乙两机床性能是否都一样好? 这反映出,对一组数据,除需要了解它们的平均水平以外,还常常需要了解它们的波动大小(即偏离平均数的大小). 描述一组数据的波动大小,可以采用不止一种办法.本课介绍“方差”即是一种方法. 2.2方差和标准差
来衡量这组数据的波动大小,并把它叫做这组数据的方差.一组数据方差越大,说明这组数据波动越大 请计算引例中机床甲、乙两组数据的方差 从0.026>0.008可以比较出,机床甲生产的10个零件直径比机床乙生产的10个零件直径波动要大 例1 已知两组数据:
分别计算这两组数据的方差. (1)求平均数 分析(2)求方差 (3)比较方差得出结论 用来衡量一组数据的波动的方法还可用一组
数据的标准差,即 公式④(即标准差)也是用来衡量一组数据波动
大小的重要的量.如
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
