小升初分班考重点专题:立体图形-2023-2024学年数学六年级下册北师大版(含答案)
文档属性
| 名称 | 小升初分班考重点专题:立体图形-2023-2024学年数学六年级下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 499.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-28 09:52:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考重点专题:立体图形-2023-2024学年数学六年级下册北师大版
一、选择题
1.一个长方体水缸,长20厘米,宽15厘米,将一块石头投入水中(石头全部浸没)水面上升2厘米,这块石头体积的计算算式是( )。
A. B.
C. D.
2.用8个棱长1厘米的正方体拼成一个长方体,拼成的长方体表面积最大为( )平方厘米。
A.24 B.34 C.48 D.28
3.一个底面是正方形的长方体纸盒,将它的侧面展开正好是一个边长为12厘米的正方形(如图)。这个纸盒的表面积是( )平方厘米。
A.144 B.153 C.162 D.108
4.如图,小丽将装有水的密闭圆柱形玻璃杯水平放置,此时水面的形状是( )。
A.平行四边形 B.圆形 C.长方形 D.半个圆柱
5.一个圆柱和一个圆锥等底等高,它们体积和是60立方厘米,圆柱的体积是( )立方厘米。
A.15 B.20 C.40 D.45
6.“等积变形”的数学思想方法是指图形或物体的形状改变,但是面积或体积不变。下面运用了“等积变形”这一思想方法的有( )。
A.①③ B.①②③ C.①②③④ D.④
二、填空题
7.如图,一块长方体木料的长是8分米,横截面是边长2分米的正方形,它的体积是( )立方分米。
8.将5个棱长为1分米的小正方体排成一排,排成的长方体表面积是( )平方分米,体积是( )立方分米。
9.等底等高的圆柱和圆锥,圆柱的体积比圆锥大42dm3,圆柱的体积是( )dm3,圆锥的体积是( )dm3。
10.一个长方体、一个圆柱和一个圆锥,它们的底面积和体积分别相等,如果长方体的高是6厘米,那么圆锥的高是( )厘米。
11.一个圆柱体的侧面展开图是一个正方形,这个正方形的边长是6.28厘米,那么这个圆柱体的底面半径是( )厘米,体积是( )立方厘米。(结果保留整数)
12.节约用水是我们每个小学生的义务。学校用的自来水管内直径为0.2分米,自来水的流速一般为每秒5分米,如果你忘记关上水龙头,一分你将浪费( )升水。
三、判断题
13.棱长是2厘米的正方体,它的表面积和体积相等。( )
14.如果一个长方体有两个相邻的面是正方形,那么这个长方体就是正方体。( )
15.把一块圆柱形橡皮泥揉成一个与它等底等体积的圆锥,高将缩小到原来的。( )
16.一个圆柱与圆锥等底等高,圆柱的体积比圆锥多18m3,圆锥的体积是9m3。( )
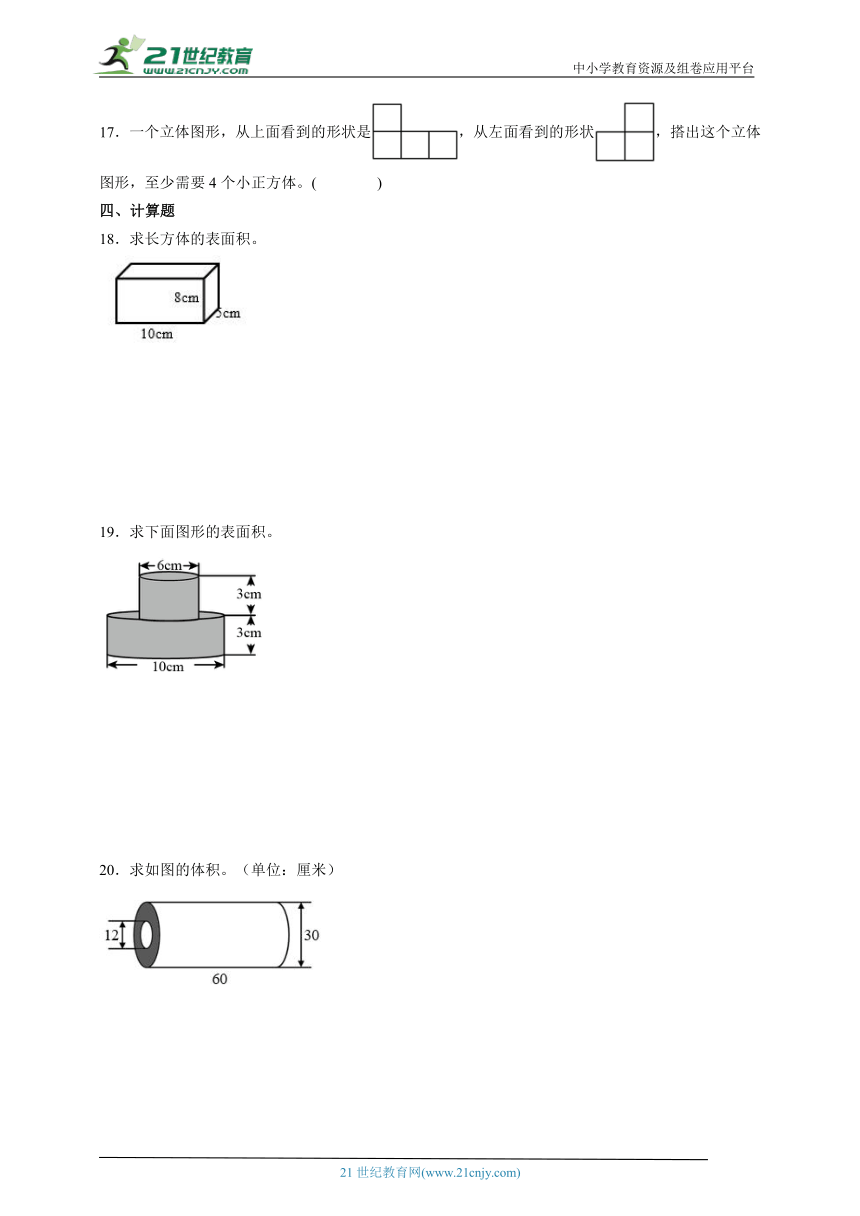
17.一个立体图形,从上面看到的形状是,从左面看到的形状,搭出这个立体图形,至少需要4个小正方体。( )
四、计算题
18.求长方体的表面积。
19.求下面图形的表面积。
20.求如图的体积。(单位:厘米)
五、解答题
21.有一个三层生日蛋糕,每一层都是长方体,最上层的长、宽、高是中间层的长、宽、高的,而中间层的长、宽、高是最下层长、宽、高的,已知最下层的长、宽、高分别是30厘米、24厘米、12厘米,则这个三层生日蛋糕的表面积是多少?
22.在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?
23.课堂上,贝贝在课桌上摆了一个高15厘米的圆柱,再在这个圆柱的上面摆一个与原来圆柱底面积相同的圆柱,此时摆成的大圆柱的高比原来圆柱的高增加了1厘米,它的侧面积增加了100.48平方厘米。原来圆柱的表面积是多少平方厘米?
24.一个铜零件的形状如图所示。每立方厘米的铜的质量约9克,制作这样一个零件大约需要多少千克铜?(结果保留整数,单位:厘米)
25.单板U形池比赛在一个形状类似U形的槽子里进行,结构由宽阔平坦的底部和两侧的四分之一的圆管组成(如图),请计算出U形池池面的面积。
26.在数学实践课上,张老师和4名同学在测量一些螺丝钉的体积,他们合作进行如下的测量与操作。乐乐准备一个圆柱形玻璃杯,从里面测量,得到底面半径为5厘米,高为20厘米;欢欢往玻璃杯里注入一些水,水的高度与水面到杯口的距离之比为1∶1;丁丁把200枚螺丝钉放入(螺丝钉完全浸没水中);宁宁测量了此时水的高度与水面到杯口的距离之比是5∶3。根据上面的信息,你能计算出一枚螺丝钉的体积大约是多少吗?(结果保留两位小数)。
参考答案:
1.A
【分析】因为石头完全浸没在水中,所以石头的体积等于上升的水的体积,上升的水的体积等于长是20厘米,宽15厘米,高是2厘米的长方体的体积,根据长方体体积长×宽×高,计算即可。
【详解】20×15×2
=300×2
=600(立方厘米)
这块石头体积的计算算式是20×15×2。
故答案为:A
2.B
【分析】正方体拼成的长方体,正方体被遮的面越少,拼成的长方体表面积就越大。展开空间想象可知:拼成的表面积最大的长方体的长为8厘米,宽为1厘米,高为1厘米。据此,结合长方体表面积公式求出它的表面积即可。
【详解】(8×1+8×1+1×1)×2
=17×2
=34(平方厘米)
故答案为:B
【点睛】本题考查了长方体的表面积,灵活运用长方体的表面积公式是解题的关键。
3.C
【分析】看图可知,侧面展开的正方形边长÷4=底面正方形的边长,这个纸盒的表面积=侧面展开的正方形边长×边长+底面正方形的边长×边长×2,据此列式计算。
【详解】12÷4=3(厘米)
12×12+3×3×2
=144+18
=162(平方厘米)
这个纸盒的表面积是162平方厘米。
故答案为:C
4.C
【分析】沿着圆柱的底面垂直切开,得到的面是长方形,观察图形可知,由于水平面与圆柱的底面垂直,水面形状是长方形,据此解答。
【详解】根据分析可知,如图,小丽将装有水的密闭圆柱形玻璃杯水平放置,此时水面的形状是长方形。
故答案为:C
5.D
【分析】等底等高的圆锥的体积是圆柱,设圆柱的体积为V立方厘米,则圆锥的体积为V,再根据等量关系:圆柱的体积+圆锥的体积=60,据此列方程解答即可。
【详解】解:设圆柱的体积为V立方厘米,则圆锥的体积为V。
V+V=60
V=60
V÷=60÷
V=60×
V=45
则圆柱的体积是45立方厘米。
故答案为:D
6.B
【分析】①观察图形可知,利用排水法求正方体木块的体积,即将正方体木块的体积转化为圆柱的体积,形状改变,但体积不变,符合等积变形这一思想方法;
②将两个不规则图形合并长方形,进而根据长方形的面积的计算方法求得两个不规则图形的面积之和,形状改变,但面积不变,符合等积变形这一思想方法;
③将圆锥沙堆转化为长方体沙堆,形状虽改变,但体积不变,符合等积变形这一思想方法;
④求阴影部分的面积,用圆的面积减去中间正方形的面积即可,阴影部分的形状没有发生变化,不符合等积变形这一思想方法。
【详解】由分析可知:
运用了“等积变形”这一思想方法的有①②③。
故答案为:B
7.32
【分析】先根据正方形面积公式:S=a2,求出底面面积,再用长方体体积公式:V=Sh,代入数据求出该长方体的体积即可。
【详解】由分析可得:
2×2×8
=4×8
=32(立方分米)
综上所述:一块长方体木料的长是8分米,横截面是边长2分米的正方形,它的体积是32立方分米。
8. 22 5
【详解】略
9. 63 21
【分析】等底等高的圆柱和圆锥,圆柱体积是圆锥体积的3倍,用体积差除以倍数差,即可求出一倍数,即圆锥体积。再用圆锥体积×3=圆柱体积,据此解题即可。
【详解】圆锥的体积:
=
=21(dm3)
圆柱的体积:
(dm3)
等底等高的圆柱和圆锥,圆柱的体积比圆锥大42dm3,圆柱的体积是(63)dm3,圆锥的体积是(21)dm3。
10.18
【分析】根据长方体体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×,它们的底面积和体积分别相等,由此可知,长方体的高=圆锥的高×;圆锥的高=长方体的高×3,据此解答。
【详解】6×3=18(厘米)
一个长方体、一个圆柱和一个圆锥,它们的底面积和体积分别相等,如果长方体的高是6厘米,那么圆锥的高是18厘米。
11. 1 20
【分析】根据题意,圆柱体的侧面展开图是一个正方形,这个正方形的边长是6.28厘米,也就是圆柱的底面周长是6.28厘米,根据周长公式:C=2πr,可推出r=C÷2π,将数据代入可求出该圆柱底面的半径;
根据圆的面积公式:S=πr2,代入数值求出底面面积,侧面展开图正方形的边长就是该圆柱的高,最后根据圆柱体积公式:V=Sh,求出该圆柱体积即可。
取一个小数的近似数用四舍五入法:在取小数近似数的时候,如果尾数的最高位数字是4或者比4小,就把尾数去掉,如果尾数的最高位是5或者比5大,就把尾数舍去并且在它的前一位进“1”。
【详解】由分析可得:
6.28÷2÷3.14
=3.14÷3.14
=1(厘米)
3.14×12=3.14(平方厘米)
3.14×6.28=19.7192(立方厘米)≈20(立方厘米)
综上所述:一个圆柱体的侧面展开图是一个正方形,这个正方形的边长是6.28厘米,那么这个圆柱体的底面半径是1厘米,体积是20立方厘米。
12.9.42
【分析】可将每秒钟流水的量看作底面直径为0.2分米,高为5分米的圆柱体体积,根据圆柱的体积公式求出每秒浪费水的体积,再乘60即为一分钟浪费水的量,结果为立方分米,再将单位换算为升即可。1立方分米=1升。
【详解】1分=60秒
(立方分米)
9.42立方分米=9.42升
即如果忘记关上水龙头,一分将浪费9.42升水。
13.×
【分析】正方体的表面积是指正方体6个面的面积之和,而正方体的体积是指它所占空间的大小,二者不是同类量,无法进行比较,据此判断。
【详解】因为表面积和体积不是同类量,所以无法进行比较,因此题干中的说法是错误的。
故答案为:×
【点睛】解答本题的关键是明确只有同类量,才能比较大小。
14.√
【分析】根据长方体的特征,当一个长方体有两个相邻的面是正方形,则这个长方体的长、宽、高是相等的,那么这个长方体也就是正方体。
【详解】据分析可知,如果一个长方体有两个相邻的面是正方形,那么这个长方体就是正方体;说法正确。
故答案为:√
【点睛】此题考查了长方体与正方体的区别与联系,关键熟悉图形特征。
15.×
【分析】根据等底等体积的圆锥的高是圆柱高的3倍,据此判断即可。
【详解】把一块圆柱形橡皮泥揉成与它等底等体积的圆锥,高将扩大到原来的3倍;所以题干说法错误。
故答案为:×
【点睛】解答此题的关键是,结合等底等高的圆锥形的体积是圆柱形体积的。
16.√
【分析】把圆柱的体积看作单位“1”,圆柱与圆锥等底等高时,圆锥的体积是圆柱体积的,根据“量÷对应的分率”求出圆柱的体积,圆锥的体积=圆柱的体积×。
【详解】圆柱的体积:18÷(1-)
=18÷
=27(m3)
圆锥的体积:27×=9(m3)
故答案为:√
【点睛】掌握圆柱与圆锥的体积关系是解答题目的关键。
17.×
【分析】从上面看到的形状是,说明这个立体图形有4列,每列至少1个小正方体;从左面看到的形状是,说明这个立体图形有两层,最底层一定有4个小正方体,上面一层至少1个小正方体,据此解答。
【详解】根据题意可得,这个立体图形有两层,最底层一定有4个小正方体,上面一层至少1个小正方体,4+1=5(个),所以搭出这个立体图形,至少需要5个小正方体。
故答案为:×
【点睛】解答本题的关键是要根据从不同方向看到的块数进行分析解答。
18.340平方厘米
【分析】把长方体的长、宽、高的数据代入长方体的表面积公式:S=(a×b+a×h+b×h)×2中,计算出长方体的表面积即可。
【详解】(10×5+10×8+5×8)×2
=(50+80+40)×2
=170×2
=340(平方厘米)
即长方体的表面积是340平方厘米。
19.307.72cm2
【分析】观察图形可知,小圆柱和大圆柱有重合的部分,把小圆柱的上底面向下平移,补给大圆柱的上底面;这样大圆柱的表面积是侧面积和2个底面积之和,而小圆柱只需计算侧面积即可;所以组合图形的表面积=大圆柱的侧面积+大圆柱的2个底面积+小圆柱的侧面积;根据公式S侧=πdh,S底=πr2,代入数据计算求解。
【详解】3.14×10×3+3.14×(10÷2)2×2+3.14×6×3
=3.14×30+3.14×25×2+3.14×18
=94.2+157+56.52
=307.72(cm2)
图形的表面积是307.72cm2。
20.35607.6立方厘米
【分析】观察图形可知,立体图形的体积=底面积×高,底面积是一个内圆直径是12厘米、外面直径是30厘米的圆环面积,高是60厘米,根据圆环的面积:S=π(R2-r2),用3.14×[(30÷2)2-(12÷2)2]×60即可求出图形的体积。
【详解】3.14×[(30÷2)2-(12÷2)2]×60
=3.14×[152-62]×60
=3.14×[225-36]×60
=3.14×189×60
=35607.6(立方厘米)
立体图形的体积是35607.6立方厘米。
21.3096平方厘米
【详解】中间层:长=15厘米,宽=12厘米,高=6厘米
上层:长=5厘米,宽=4厘米,高=2厘米
(30×24+30×12+12×24+15×12+15×6+12×6+5×4+5×2+4×2)×2-15×12×2-5×4×2=3096(平方厘米)
22.15000平方厘米
【分析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑,变化前后的表面积不变,由此解答即可。
【详解】50×50×6
=2500×6
=15000(平方厘米)
答:剩下的立体图形的表面积是15000平方厘米。
【点睛】明确变化前后的表面积不变是解答本题的关键。
23.3114.88平方厘米
【分析】
根据题意,增加的圆柱和原来圆柱的底面积相同,那么增加的圆柱的底面周长、底面半径与原来圆柱的底面周长、底面半径相等。
已知摆成的大圆柱的高比原来圆柱的高增加了1厘米,那么增加的表面积即是高为1厘米的圆柱侧面积,根据S侧=Ch可知,C=S侧÷h,由此求出增加的圆柱的底面周长。
再根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆柱的底面半径。
最后根据圆柱的表面积公式S表=S侧+2S底,其中S侧=Ch,S底=πr2,代入数据计算求出原来圆柱的表面积。
【详解】圆柱的底面周长:100.48÷1=100.48(厘米)
圆柱的底面半径:
100.48÷3.14÷2
=32÷2
=16(厘米)
圆柱的表面积:
100.48×15+3.14×162×2
=1507.2+3.14×256×2
=1507.2+1607.68
=3114.88(平方厘米)
答:原来圆柱的表面积是3114.88平方厘米。
24.54千克
【分析】
根据圆柱的体积公式V=πr h,圆锥的体积公式V=πr h,代入数据求出这个零件的体积,再用零件的体积乘每立方厘米铜的质量,最后根据1千克=1000克把结果换算成以千克为单位。
【详解】
(20÷2)2×3.14×15
=100×3.14×15
=314×15
=4710(立方厘米)
(20÷2)2×3.14×12×
=100×3.14×12×
=(100×3.14)×(12×)
=314×4
=1256(立方厘米)
4710+1256=5966(立方厘米)
5966×9=53694(克)
53694克≈54千克
答:制作这样一个零件大约需要54千克铜。
25.368.4平方米
【分析】
U型池池面的面积=圆柱侧面积的一半+底面长方形的面积。圆柱的侧面积S=2πrh,长方形的面积公式为:S=ab,据此解答即可。
【详解】20×9+×3.14×3×2×20
=180+×3.14×3×40
=180+3.14×3×20
=180+9.42×20
=180+188.4
=368.4(平方米)
答:U形池池面的面积为368.4平方米。
26.0.98立方厘米
【分析】
根据题意可知,未放入螺丝钉时,水的高度与水面到杯口的距离之比为1∶1,则水的高度占玻璃杯高度的=,放入螺丝钉后,水的高度与水面到杯口的距离之比是5∶3,则水的高度占玻璃高度的=,玻璃杯高20厘米,求出上升部分水的高度,已知底面半径为5厘米,根据圆柱的体积公式V=πr2h求出上升部分水的体积200枚螺丝钉的体积,把数据代入公式求出200枚螺丝钉的体积,然后除以200即可求出1枚螺丝钉的体积。据此解答。
【详解】20×
=20×
=10(厘米)
20×
=20×
=
=12.5(厘米)
12.5-10=2.5(厘米)
3.14×52×2.5
=3.14×25×2.5
=78.5×2.5
=196.25(立方厘米)
196.25÷200=0.98125≈0.98(立方厘米)
答:一枚螺丝钉的体积大约是0.98立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考重点专题:立体图形-2023-2024学年数学六年级下册北师大版
一、选择题
1.一个长方体水缸,长20厘米,宽15厘米,将一块石头投入水中(石头全部浸没)水面上升2厘米,这块石头体积的计算算式是( )。
A. B.
C. D.
2.用8个棱长1厘米的正方体拼成一个长方体,拼成的长方体表面积最大为( )平方厘米。
A.24 B.34 C.48 D.28
3.一个底面是正方形的长方体纸盒,将它的侧面展开正好是一个边长为12厘米的正方形(如图)。这个纸盒的表面积是( )平方厘米。
A.144 B.153 C.162 D.108
4.如图,小丽将装有水的密闭圆柱形玻璃杯水平放置,此时水面的形状是( )。
A.平行四边形 B.圆形 C.长方形 D.半个圆柱
5.一个圆柱和一个圆锥等底等高,它们体积和是60立方厘米,圆柱的体积是( )立方厘米。
A.15 B.20 C.40 D.45
6.“等积变形”的数学思想方法是指图形或物体的形状改变,但是面积或体积不变。下面运用了“等积变形”这一思想方法的有( )。
A.①③ B.①②③ C.①②③④ D.④
二、填空题
7.如图,一块长方体木料的长是8分米,横截面是边长2分米的正方形,它的体积是( )立方分米。
8.将5个棱长为1分米的小正方体排成一排,排成的长方体表面积是( )平方分米,体积是( )立方分米。
9.等底等高的圆柱和圆锥,圆柱的体积比圆锥大42dm3,圆柱的体积是( )dm3,圆锥的体积是( )dm3。
10.一个长方体、一个圆柱和一个圆锥,它们的底面积和体积分别相等,如果长方体的高是6厘米,那么圆锥的高是( )厘米。
11.一个圆柱体的侧面展开图是一个正方形,这个正方形的边长是6.28厘米,那么这个圆柱体的底面半径是( )厘米,体积是( )立方厘米。(结果保留整数)
12.节约用水是我们每个小学生的义务。学校用的自来水管内直径为0.2分米,自来水的流速一般为每秒5分米,如果你忘记关上水龙头,一分你将浪费( )升水。
三、判断题
13.棱长是2厘米的正方体,它的表面积和体积相等。( )
14.如果一个长方体有两个相邻的面是正方形,那么这个长方体就是正方体。( )
15.把一块圆柱形橡皮泥揉成一个与它等底等体积的圆锥,高将缩小到原来的。( )
16.一个圆柱与圆锥等底等高,圆柱的体积比圆锥多18m3,圆锥的体积是9m3。( )
17.一个立体图形,从上面看到的形状是,从左面看到的形状,搭出这个立体图形,至少需要4个小正方体。( )
四、计算题
18.求长方体的表面积。
19.求下面图形的表面积。
20.求如图的体积。(单位:厘米)
五、解答题
21.有一个三层生日蛋糕,每一层都是长方体,最上层的长、宽、高是中间层的长、宽、高的,而中间层的长、宽、高是最下层长、宽、高的,已知最下层的长、宽、高分别是30厘米、24厘米、12厘米,则这个三层生日蛋糕的表面积是多少?
22.在一个棱长为50厘米的正方体木块,在它的八个角上各挖去一个棱长为5厘米的小正方体,问剩下的立体图形的表面积是多少?
23.课堂上,贝贝在课桌上摆了一个高15厘米的圆柱,再在这个圆柱的上面摆一个与原来圆柱底面积相同的圆柱,此时摆成的大圆柱的高比原来圆柱的高增加了1厘米,它的侧面积增加了100.48平方厘米。原来圆柱的表面积是多少平方厘米?
24.一个铜零件的形状如图所示。每立方厘米的铜的质量约9克,制作这样一个零件大约需要多少千克铜?(结果保留整数,单位:厘米)
25.单板U形池比赛在一个形状类似U形的槽子里进行,结构由宽阔平坦的底部和两侧的四分之一的圆管组成(如图),请计算出U形池池面的面积。
26.在数学实践课上,张老师和4名同学在测量一些螺丝钉的体积,他们合作进行如下的测量与操作。乐乐准备一个圆柱形玻璃杯,从里面测量,得到底面半径为5厘米,高为20厘米;欢欢往玻璃杯里注入一些水,水的高度与水面到杯口的距离之比为1∶1;丁丁把200枚螺丝钉放入(螺丝钉完全浸没水中);宁宁测量了此时水的高度与水面到杯口的距离之比是5∶3。根据上面的信息,你能计算出一枚螺丝钉的体积大约是多少吗?(结果保留两位小数)。
参考答案:
1.A
【分析】因为石头完全浸没在水中,所以石头的体积等于上升的水的体积,上升的水的体积等于长是20厘米,宽15厘米,高是2厘米的长方体的体积,根据长方体体积长×宽×高,计算即可。
【详解】20×15×2
=300×2
=600(立方厘米)
这块石头体积的计算算式是20×15×2。
故答案为:A
2.B
【分析】正方体拼成的长方体,正方体被遮的面越少,拼成的长方体表面积就越大。展开空间想象可知:拼成的表面积最大的长方体的长为8厘米,宽为1厘米,高为1厘米。据此,结合长方体表面积公式求出它的表面积即可。
【详解】(8×1+8×1+1×1)×2
=17×2
=34(平方厘米)
故答案为:B
【点睛】本题考查了长方体的表面积,灵活运用长方体的表面积公式是解题的关键。
3.C
【分析】看图可知,侧面展开的正方形边长÷4=底面正方形的边长,这个纸盒的表面积=侧面展开的正方形边长×边长+底面正方形的边长×边长×2,据此列式计算。
【详解】12÷4=3(厘米)
12×12+3×3×2
=144+18
=162(平方厘米)
这个纸盒的表面积是162平方厘米。
故答案为:C
4.C
【分析】沿着圆柱的底面垂直切开,得到的面是长方形,观察图形可知,由于水平面与圆柱的底面垂直,水面形状是长方形,据此解答。
【详解】根据分析可知,如图,小丽将装有水的密闭圆柱形玻璃杯水平放置,此时水面的形状是长方形。
故答案为:C
5.D
【分析】等底等高的圆锥的体积是圆柱,设圆柱的体积为V立方厘米,则圆锥的体积为V,再根据等量关系:圆柱的体积+圆锥的体积=60,据此列方程解答即可。
【详解】解:设圆柱的体积为V立方厘米,则圆锥的体积为V。
V+V=60
V=60
V÷=60÷
V=60×
V=45
则圆柱的体积是45立方厘米。
故答案为:D
6.B
【分析】①观察图形可知,利用排水法求正方体木块的体积,即将正方体木块的体积转化为圆柱的体积,形状改变,但体积不变,符合等积变形这一思想方法;
②将两个不规则图形合并长方形,进而根据长方形的面积的计算方法求得两个不规则图形的面积之和,形状改变,但面积不变,符合等积变形这一思想方法;
③将圆锥沙堆转化为长方体沙堆,形状虽改变,但体积不变,符合等积变形这一思想方法;
④求阴影部分的面积,用圆的面积减去中间正方形的面积即可,阴影部分的形状没有发生变化,不符合等积变形这一思想方法。
【详解】由分析可知:
运用了“等积变形”这一思想方法的有①②③。
故答案为:B
7.32
【分析】先根据正方形面积公式:S=a2,求出底面面积,再用长方体体积公式:V=Sh,代入数据求出该长方体的体积即可。
【详解】由分析可得:
2×2×8
=4×8
=32(立方分米)
综上所述:一块长方体木料的长是8分米,横截面是边长2分米的正方形,它的体积是32立方分米。
8. 22 5
【详解】略
9. 63 21
【分析】等底等高的圆柱和圆锥,圆柱体积是圆锥体积的3倍,用体积差除以倍数差,即可求出一倍数,即圆锥体积。再用圆锥体积×3=圆柱体积,据此解题即可。
【详解】圆锥的体积:
=
=21(dm3)
圆柱的体积:
(dm3)
等底等高的圆柱和圆锥,圆柱的体积比圆锥大42dm3,圆柱的体积是(63)dm3,圆锥的体积是(21)dm3。
10.18
【分析】根据长方体体积公式:体积=底面积×高;圆锥的体积公式:体积=底面积×高×,它们的底面积和体积分别相等,由此可知,长方体的高=圆锥的高×;圆锥的高=长方体的高×3,据此解答。
【详解】6×3=18(厘米)
一个长方体、一个圆柱和一个圆锥,它们的底面积和体积分别相等,如果长方体的高是6厘米,那么圆锥的高是18厘米。
11. 1 20
【分析】根据题意,圆柱体的侧面展开图是一个正方形,这个正方形的边长是6.28厘米,也就是圆柱的底面周长是6.28厘米,根据周长公式:C=2πr,可推出r=C÷2π,将数据代入可求出该圆柱底面的半径;
根据圆的面积公式:S=πr2,代入数值求出底面面积,侧面展开图正方形的边长就是该圆柱的高,最后根据圆柱体积公式:V=Sh,求出该圆柱体积即可。
取一个小数的近似数用四舍五入法:在取小数近似数的时候,如果尾数的最高位数字是4或者比4小,就把尾数去掉,如果尾数的最高位是5或者比5大,就把尾数舍去并且在它的前一位进“1”。
【详解】由分析可得:
6.28÷2÷3.14
=3.14÷3.14
=1(厘米)
3.14×12=3.14(平方厘米)
3.14×6.28=19.7192(立方厘米)≈20(立方厘米)
综上所述:一个圆柱体的侧面展开图是一个正方形,这个正方形的边长是6.28厘米,那么这个圆柱体的底面半径是1厘米,体积是20立方厘米。
12.9.42
【分析】可将每秒钟流水的量看作底面直径为0.2分米,高为5分米的圆柱体体积,根据圆柱的体积公式求出每秒浪费水的体积,再乘60即为一分钟浪费水的量,结果为立方分米,再将单位换算为升即可。1立方分米=1升。
【详解】1分=60秒
(立方分米)
9.42立方分米=9.42升
即如果忘记关上水龙头,一分将浪费9.42升水。
13.×
【分析】正方体的表面积是指正方体6个面的面积之和,而正方体的体积是指它所占空间的大小,二者不是同类量,无法进行比较,据此判断。
【详解】因为表面积和体积不是同类量,所以无法进行比较,因此题干中的说法是错误的。
故答案为:×
【点睛】解答本题的关键是明确只有同类量,才能比较大小。
14.√
【分析】根据长方体的特征,当一个长方体有两个相邻的面是正方形,则这个长方体的长、宽、高是相等的,那么这个长方体也就是正方体。
【详解】据分析可知,如果一个长方体有两个相邻的面是正方形,那么这个长方体就是正方体;说法正确。
故答案为:√
【点睛】此题考查了长方体与正方体的区别与联系,关键熟悉图形特征。
15.×
【分析】根据等底等体积的圆锥的高是圆柱高的3倍,据此判断即可。
【详解】把一块圆柱形橡皮泥揉成与它等底等体积的圆锥,高将扩大到原来的3倍;所以题干说法错误。
故答案为:×
【点睛】解答此题的关键是,结合等底等高的圆锥形的体积是圆柱形体积的。
16.√
【分析】把圆柱的体积看作单位“1”,圆柱与圆锥等底等高时,圆锥的体积是圆柱体积的,根据“量÷对应的分率”求出圆柱的体积,圆锥的体积=圆柱的体积×。
【详解】圆柱的体积:18÷(1-)
=18÷
=27(m3)
圆锥的体积:27×=9(m3)
故答案为:√
【点睛】掌握圆柱与圆锥的体积关系是解答题目的关键。
17.×
【分析】从上面看到的形状是,说明这个立体图形有4列,每列至少1个小正方体;从左面看到的形状是,说明这个立体图形有两层,最底层一定有4个小正方体,上面一层至少1个小正方体,据此解答。
【详解】根据题意可得,这个立体图形有两层,最底层一定有4个小正方体,上面一层至少1个小正方体,4+1=5(个),所以搭出这个立体图形,至少需要5个小正方体。
故答案为:×
【点睛】解答本题的关键是要根据从不同方向看到的块数进行分析解答。
18.340平方厘米
【分析】把长方体的长、宽、高的数据代入长方体的表面积公式:S=(a×b+a×h+b×h)×2中,计算出长方体的表面积即可。
【详解】(10×5+10×8+5×8)×2
=(50+80+40)×2
=170×2
=340(平方厘米)
即长方体的表面积是340平方厘米。
19.307.72cm2
【分析】观察图形可知,小圆柱和大圆柱有重合的部分,把小圆柱的上底面向下平移,补给大圆柱的上底面;这样大圆柱的表面积是侧面积和2个底面积之和,而小圆柱只需计算侧面积即可;所以组合图形的表面积=大圆柱的侧面积+大圆柱的2个底面积+小圆柱的侧面积;根据公式S侧=πdh,S底=πr2,代入数据计算求解。
【详解】3.14×10×3+3.14×(10÷2)2×2+3.14×6×3
=3.14×30+3.14×25×2+3.14×18
=94.2+157+56.52
=307.72(cm2)
图形的表面积是307.72cm2。
20.35607.6立方厘米
【分析】观察图形可知,立体图形的体积=底面积×高,底面积是一个内圆直径是12厘米、外面直径是30厘米的圆环面积,高是60厘米,根据圆环的面积:S=π(R2-r2),用3.14×[(30÷2)2-(12÷2)2]×60即可求出图形的体积。
【详解】3.14×[(30÷2)2-(12÷2)2]×60
=3.14×[152-62]×60
=3.14×[225-36]×60
=3.14×189×60
=35607.6(立方厘米)
立体图形的体积是35607.6立方厘米。
21.3096平方厘米
【详解】中间层:长=15厘米,宽=12厘米,高=6厘米
上层:长=5厘米,宽=4厘米,高=2厘米
(30×24+30×12+12×24+15×12+15×6+12×6+5×4+5×2+4×2)×2-15×12×2-5×4×2=3096(平方厘米)
22.15000平方厘米
【分析】对于和长方体相关的立体图形表面积,一般从上下、左右、前后3个方向考虑,变化前后的表面积不变,由此解答即可。
【详解】50×50×6
=2500×6
=15000(平方厘米)
答:剩下的立体图形的表面积是15000平方厘米。
【点睛】明确变化前后的表面积不变是解答本题的关键。
23.3114.88平方厘米
【分析】
根据题意,增加的圆柱和原来圆柱的底面积相同,那么增加的圆柱的底面周长、底面半径与原来圆柱的底面周长、底面半径相等。
已知摆成的大圆柱的高比原来圆柱的高增加了1厘米,那么增加的表面积即是高为1厘米的圆柱侧面积,根据S侧=Ch可知,C=S侧÷h,由此求出增加的圆柱的底面周长。
再根据圆的周长公式C=2πr可知,r=C÷π÷2,由此求出圆柱的底面半径。
最后根据圆柱的表面积公式S表=S侧+2S底,其中S侧=Ch,S底=πr2,代入数据计算求出原来圆柱的表面积。
【详解】圆柱的底面周长:100.48÷1=100.48(厘米)
圆柱的底面半径:
100.48÷3.14÷2
=32÷2
=16(厘米)
圆柱的表面积:
100.48×15+3.14×162×2
=1507.2+3.14×256×2
=1507.2+1607.68
=3114.88(平方厘米)
答:原来圆柱的表面积是3114.88平方厘米。
24.54千克
【分析】
根据圆柱的体积公式V=πr h,圆锥的体积公式V=πr h,代入数据求出这个零件的体积,再用零件的体积乘每立方厘米铜的质量,最后根据1千克=1000克把结果换算成以千克为单位。
【详解】
(20÷2)2×3.14×15
=100×3.14×15
=314×15
=4710(立方厘米)
(20÷2)2×3.14×12×
=100×3.14×12×
=(100×3.14)×(12×)
=314×4
=1256(立方厘米)
4710+1256=5966(立方厘米)
5966×9=53694(克)
53694克≈54千克
答:制作这样一个零件大约需要54千克铜。
25.368.4平方米
【分析】
U型池池面的面积=圆柱侧面积的一半+底面长方形的面积。圆柱的侧面积S=2πrh,长方形的面积公式为:S=ab,据此解答即可。
【详解】20×9+×3.14×3×2×20
=180+×3.14×3×40
=180+3.14×3×20
=180+9.42×20
=180+188.4
=368.4(平方米)
答:U形池池面的面积为368.4平方米。
26.0.98立方厘米
【分析】
根据题意可知,未放入螺丝钉时,水的高度与水面到杯口的距离之比为1∶1,则水的高度占玻璃杯高度的=,放入螺丝钉后,水的高度与水面到杯口的距离之比是5∶3,则水的高度占玻璃高度的=,玻璃杯高20厘米,求出上升部分水的高度,已知底面半径为5厘米,根据圆柱的体积公式V=πr2h求出上升部分水的体积200枚螺丝钉的体积,把数据代入公式求出200枚螺丝钉的体积,然后除以200即可求出1枚螺丝钉的体积。据此解答。
【详解】20×
=20×
=10(厘米)
20×
=20×
=
=12.5(厘米)
12.5-10=2.5(厘米)
3.14×52×2.5
=3.14×25×2.5
=78.5×2.5
=196.25(立方厘米)
196.25÷200=0.98125≈0.98(立方厘米)
答:一枚螺丝钉的体积大约是0.98立方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
