小升初分班考重点专题:平面图形-2023-2024学年数学六年级下册北师大版(含解析)
文档属性
| 名称 | 小升初分班考重点专题:平面图形-2023-2024学年数学六年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 581.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-28 10:07:42 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初分班考重点专题:平面图形-2023-2024学年数学六年级下册北师大版
一、选择题
1.下面几幅图中,三角形被遮住了一部分,不能直接确定三角形种类的是( )。
A. B.
C. D.
2.某市计划扩建一个长方形绿化带,若长增加12米,宽不变,面积就增加144平方米;若宽增加8米,长不变,面积也增加144平方米。这个绿化带原来的面积是( )平方米。
A.96 B.104 C.124 D.216
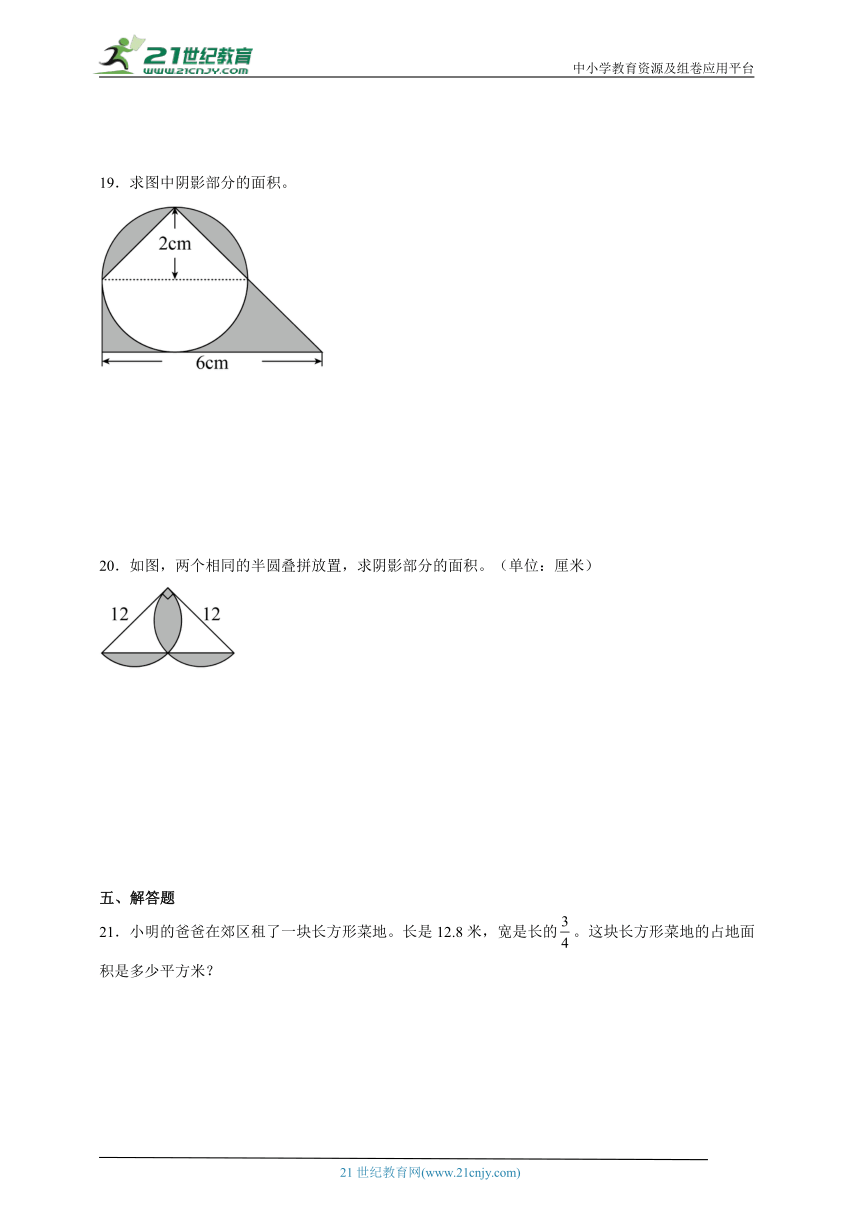
3.如图,用两个完全一样的等腰梯形拼成一个平行四边形,每个梯形的周长是( )厘米。
A.35 B.50 C.55 D.70
4.一个圆柱的高与底面直径相等,将圆柱的侧面沿高剪开,得到的长方形的长和宽的比是( )。
A.1∶1 B.π∶1 C.1∶π D.1∶2
5.长方形的长和宽都扩大2倍,它的面积扩大( )倍。
A.2 B.4 C.8 D.10
6.一个钟表的分钟长10厘米,从3时走到5时,分针尖端走过来( )厘米。
A.31.4 B.62.8 C.125.6 D.50.24
二、填空题
7.王师傅想要加工一个三角形自行车支架,两根钢管的长度分别是6分米和5分米,第三根最短( )分米,最长( )分米(取整分米数)。支架做成三角形的依据是( )。
8.一个平行四边形相邻两边的长度是5厘米和8厘米,平行四边形的周长是( )厘米。
9.一个等腰梯形周长是60厘米,上底是7厘米,下底是9厘米,腰长是( )厘米。
10.一块长方形绿地宽9米,面积是450平方米,如果宽增加到36米,而长不变,扩大后的长方形绿地的面积是( )平方米。
11.甲圆的半径等于乙圆的直径,则甲圆和乙圆面积的比是( )∶( )。
12.一个圆形花坛的半径是12米,将它改造成一个正方形花坛,但不改变花坛的周长,则正方形花坛的边长是( )米。
三、判断题
13.下图中,a∥b,三个图形的面积相等。( )
14.如图平行四边形的面积一定小于50平方厘米。( )
15.一个梯形的高不变,上底增加4cm,下底减少4cm,它的面积与原来的面积相等。( )
16.在同一个圆中,扇形的大小与圆心角的度数无关。( )
17.一个圆的半径扩大到原来的2倍,周长也扩大到原来的2倍。( )
四、计算题
18.分别求出阴影部分的周长和面积。(单位:cm)
19.求图中阴影部分的面积。
20.如图,两个相同的半圆叠拼放置,求阴影部分的面积。(单位:厘米)
五、解答题
21.小明的爸爸在郊区租了一块长方形菜地。长是12.8米,宽是长的。这块长方形菜地的占地面积是多少平方米?
22.如图,王爷爷准备在这块地中圈出一个最大的正方形种植韭菜,其余的地方种植菠菜。请在图上画出你的设计方案,并算出韭菜地和菠菜地的面积。
23.在比例尺为1∶200的地图上,小明家的客厅长为3厘米,宽为2厘米,爸爸在装修时想用一种浅白色的方砖铺地面,经询问商店,这种方砖铺18平方米需要618块,那么请你计算一下,在不浪费的情况下,爸爸买多少块这种方砖正好够用?
24.如图,一个正六边形的边长和一个小圆的周长相等。如果这个小圆按箭头方向从某一位置沿着正六边形的周边做无滑动滚动,直至回到原出发位置。那么
(1)这个小圆滚动了多少圈?
(2)这个小圆回到原出发位置经过部分的面积是多少平方厘米?(小圆的半径为1厘米,π取3.14,结果保留两位小数。)
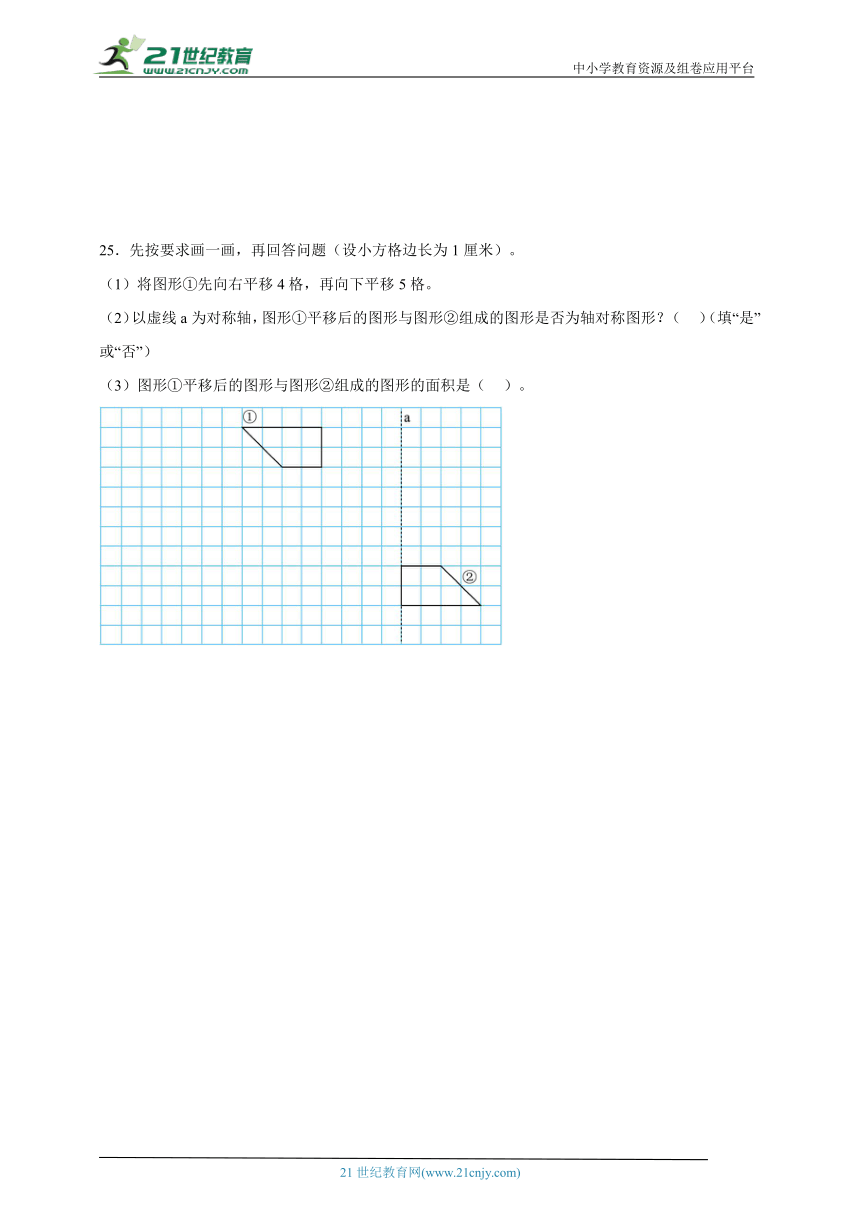
25.先按要求画一画,再回答问题(设小方格边长为1厘米)。
(1)将图形①先向右平移4格,再向下平移5格。
(2)以虚线a为对称轴,图形①平移后的图形与图形②组成的图形是否为轴对称图形?( )(填“是”或“否”)
(3)图形①平移后的图形与图形②组成的图形的面积是( )。
参考答案:
1.B
【分析】有一个角是钝角的三角形是钝角三角形,三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形;依此即可选择。
【详解】
A.此三角形漏出的角为钝角,因此这是一个钝角三角形。
B.、、此幅图中的三角形可能是直角三角形,也可能是锐角三角形,还可能是钝角三角形。
C.此三角形漏出的角为直角,因此这是一个直角三角形。
D.此三角形是一个锐角三角形。
由此可知,不能直接确定三角形种类的是。
故答案为:B
2.D
【分析】根据长方形的面积=长×宽,用增加的面积除以增加的宽求出原来的长,用增加的面积除以增加的长求出原来的宽,然后把数据代入公式即可;据此解答。
【详解】根据分析:
(144÷8)×(144÷12)
=18×12
=216(平方米)
所以这个绿化带原来的面积是216平方米。
故答案为:D
3.B
【分析】观察上图可知,等腰梯形的腰长为15厘米,梯形的上底加下底的和为20厘米,等腰梯形的周长=上底+下底+腰长×2,把数据代入计算即可解答。
【详解】20+15×2
=20+30
=50(厘米)
每个梯形的周长是50厘米。
故答案为:B
4.B
【分析】已知圆柱的侧面展开图一般是长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高;
根据比的意义写出长方形的长和宽的比,即圆柱的底面周长与高的比,已知圆柱的高与底面直径相等,据此化简比即可。
【详解】圆柱的高与底面直径相等,即h=d。
长方形的长∶宽
=圆柱的底面周长∶高
=πd∶h
=πd∶d
=π∶1
得到的长方形的长和宽的比是π∶1。
故答案为:B
5.B
【分析】长方形的面积=长×宽,积的变化规律:一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)几;那么长方形的长和宽都扩大2倍,它的面积会扩大(2×2)倍;据此解答。
【详解】根据分析:2×2=4,所以长方形的长和宽都扩大2倍,它的面积扩大4倍。
故答案为:B
6.C
【分析】1小时分针绕钟面旋转一周,分针从3时走到5时,分针绕钟面旋转两周,分钟长10厘米作圆的半径,根据圆的周长:C=2πr,求出分针绕钟面旋转一周分针尖端走过的路程,最后乘2即可。
【详解】10×2×3.14×2
=62.8×2
=125.6(厘米)
从3时走到5时,分针尖端走过来125.6厘米。
故答案为:C
7. 2 10 三角形具有稳定性
【分析】三角形具有稳定性,三角形的稳定性在实际生活中有很多应用,如相机三脚架。任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边。第三根钢管最短是(6-5+1)分米,最长是(6+5-1)分米。
【详解】6+5-1
=11-1
=10(分米)
6-5+1
=1+1
=2(分米)
王师傅想要加工一个三角形自行车支架,两根钢管的长度分别是6分米和5分米,第三根最短2分米,最长10分米,分米(取整分米数)。支架做成三角形的依据是三角形具有稳定性。
8.26
【分析】两组对边分别平行且相等的四边形,叫做平行四边形;根据平行四边形相邻两边的长度是5厘米和8厘米可知,另外两条边的长度也是5厘米和8厘米,把平行四边形4条边长度相加,即可求出平行四边形周长。
【详解】5+8+5+8=26(厘米)
即一个平行四边形相邻两边的长度是5厘米和8厘米,平行四边形的周长是26厘米。
9.22
【分析】结合等腰梯形的特征可知,等腰梯形的两腰相等。根据梯形的周长可知,用梯形周长减去其上下底之和,再除以2就是其腰长。
【详解】(60-7-9)÷2
=44÷2
=22(厘米)
其腰长为22厘米。
10.1800
【分析】先根据长方形的长=面积÷宽,求出绿地的长。再根据长方形的面积=长×宽,求出扩大后的绿地面积。
【详解】450÷9×36
=50×36
=1800(平方米)
扩大后的长方形绿地的面积是1800平方米。
11. 4 1
【分析】假设甲圆的半径是2,那么乙圆的直径是2,半径是1。根据圆的面积公式S=πr2先分别求出两个圆的面积,再求出甲圆和乙圆面积的比即可。
【详解】令甲圆半径是2,则乙圆直径是2,
2÷2=1
3.14×22
=3.14×4
=12.56
3.14×12
=3.14×1
=3.14
12.56∶3.14=(12.56÷3.14)∶(3.14÷3.14)=4∶1
所以,甲圆和乙圆面积的比是4∶1。
12.18.84
【分析】已知圆形花坛的半径是12米,根据圆的周长公式C=2πr,求出圆形花坛的周长;
将它改造成一个正方形花坛,但不改变花坛的周长,即正方形的周长等于圆的周长;根据正方形的边长=周长÷4,即可求出正方形花坛的边长。
【详解】圆的周长:
2×3.14×12=75.36(米)
正方形的边长:
75.36÷4=18.84(米)
则正方形花坛的边长是18.84米。
13.×
【分析】平行线间的距离处处相等,也就是三个图形的高都是相等的,平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,假设高是1,代入数据计算出三个图形的面积作对比即可求解。
【详解】平行四边形面积=4×1=4(cm2)
三角形面积=4×1÷2=2(cm2)
梯形的面积=(3+1)×1÷2=4×1÷2=2(cm2)
三个图形的面积不相等,原题说法错误。
故答案为:×
14.√
【分析】如下图,作出平行四边形的底10厘米对应的高h,由“直角三角形中斜边最长”可知,h小于5厘米;根据平行四边形的面积=底×高,得出平行四边形的面积与50平方厘米的大小关系。
【详解】如图:
h<5
10×h<10×5,即10h<50;
所以,平行四边形的面积一定小于50平方厘米。
原题说法正确。
故答案为:√
15.√
【分析】根据梯形的面积=(上底+下底)×高÷2可知,梯形的高不变,上底增加4cm,下底减少4cm,则上底与下底之和不变,所以梯形的面积不变。
【详解】原来梯形的面积=(上底+下底)×高÷2
现在梯形的高不变,上底增加4cm,下底减少4cm,则梯形的面积是:
(上底+4+下底-4)×高÷2=(上底+下底)×高÷2
它的面积与原来的面积相等。
原题说法正确。
故答案为:√
16.×
【分析】在同一个圆中,扇形的与扇形对应的圆心角度数密切相关,根据圆心角与扇形面积的关系,可以做出判断。
【详解】在同一个圆中,扇形的大小与这个扇形的圆心角大小有关,圆心角越大扇形越大,圆心角越小扇形越小,所以原题说法错误。
故答案为:×
17.√
【分析】圆周长=2πr,据此通过举例子的方式来判断题干的正误。
【详解】例:一个圆的半径是1,周长为2×π×1=2π。当半径扩大到原来的2倍,变成2,此时周长为2×π×2=4π。4π÷2π=2,所以周长也扩大到原来的2倍。
所以,一个圆的半径扩大到原来的2倍,周长也扩大到原来的2倍。
故答案为:√
18.周长:23.98cm;面积:10.99cm2
【分析】阴影部分周长等于半径是4cm圆的周长的一半+半径是(4-1)cm圆的周长的一半+1×2,根据圆的周长公式:周长=π×半径×2,代入数据,求出阴影部分周长;
阴影部分面积=圆环面积的一半,根据圆环面积公式:面积=π×(大圆半径2-小圆半径2),代入数据,求出圆环面积,再除以2,即可解答。
【详解】3.14×4×2÷2+3.14×(4-1)×2÷2+1×2
=12.56×2÷2+3.14×3×2÷2+2
=12.56+9.42+2
=23.98(cm)
3.14×(42-32)÷2
=3.14×(16-9)÷2
=3.14×7÷2
=21.98÷2
=10.99(cm2)
阴影周长是23.98cm,面积是10.99cm2。
19.6cm2
【分析】阴影部分面积=半径是2cm的圆的半圆面积+上底是4cm,下底是6cm,高是2cm的梯形面积-底是4cm,高是2cm的三角形面积-半径是2cm半圆的面积,由此可知,阴影部分面积=梯形面积-三角形面积,根据梯形面积公式:面积=(上底+下底)×高÷2,三角形面积公式:面积=底×高÷2,代入数据,即可解答。
【详解】(4+6)×2÷2-4×2÷2
=10×2÷2-8÷2
=20÷2-4
=10-4
=6(cm2)
20.41.04平方厘米
【分析】
如图:,4个阴影部分的面积相等,2个阴影部分面积等于半径是(12÷2)厘米的半圆面积减去底是12厘米,高是(12÷2)厘米的三角形面积,根据圆的面积公式:面积=π×半径×半径,三角形面积公式:面积=底×高÷2,代入数据,求出2个阴影部分面积,再乘2,即可解答。
【详解】3.14×(12÷2)2÷2-12×(12÷2)÷2
=3.14×62÷2-12×6÷2
=3.14×36÷2-72÷2
=113.04÷2-36
=56.52-36
=20.52(平方厘米)
20.52×2=41.04(平方厘米)
阴影部分面积是41.04平方厘米。
21.122.88平方米
【分析】先把长方形的长看作单位“1”,已知宽是长的,根据求一个数的几分之几是多少,用乘法计算,求出长方形的宽;
再根据长方形的面积=长×宽,求出这块长方形菜地的面积。
【详解】宽:12.8×=9.6(米)
面积:12.8×9.6=122.88(平方米)
答:这块长方形菜地的占地面积是122.88平方米。
22.设计方案见详解;韭菜地面积:3600平方米;菠菜地面积:1800平方米
【分析】正方形四条边相等,要将长方形围成一个最大的正方形,那么以长方形的宽作为正方形的边长,从长方形的长上取60米的长度,与宽围成一个边长为60米的正方形,这个正方形最大;然后根据正方形的面积=边长×边长,长方形的面积=长×宽;据此计算各自的面积。
【详解】设计方案如下:
韭菜地面积:60×60=3600(平方米)
菠菜地面积:(90-60)×60
=30×60
=1800(平方米)
答:韭菜地的面积为3600平方米,菠菜地的面积为1800平方米。
23.824块
【分析】根据实际距离=图上距离÷比例尺,换算出客厅实际长和宽,长方形面积=长×宽,据此求出客厅面积,铺的面积÷用的方砖块数=每块方砖面积,客厅面积÷每块方砖面积=方砖块数,据此列式解答。
【详解】3÷=3×200=600(厘米)=6(米)
2÷=2×200=400(厘米)=4(米)
6×4÷(18÷618)
=24÷
=24×
=824(块)
答:爸爸买824块这种方砖正好够用。
24.(1)7圈;
(2)87.92平方厘米
【分析】(1)小圆在滚动的过程中,除了要滚正六边形的边,还要滚动正六边形的六个角。因为正六边形的边长和一个小圆的周长相等,则小圆滚动六条边正好是六圈。滚动整个六边形是360°,则每个顶点是滚动60°,即每个顶点滚动了圈,6个顶点就是1个圈。加上滚动边的6圈,合在一起是7圈。
(2)每个顶点滚动了圈,是以顶点为圆心,小圆的直径为半径的的圆,则每个顶点经过的面积=,且半径是小圆的直径。小圆滚过每条边形成了一个长方形,这个长方形的长是小圆的周长,宽是小圆的直径。再根据长方形的面积=长×宽得出小圆的经过每条边的面积,再乘6就是6条边经过的面积。最后相加即可。
【详解】(1)360°÷6=60°
(圈)
=
(圈)
答:这个小圆滚动了7圈。
(2)
=
(平方厘米)
(平方厘米)
=
(平方厘米)
(平方厘米)
(平方厘米)
28×3.14=87.92(平方厘米)
答:这个小圆回到原出发位置经过部分的面积是87.92平方厘米。
25.(1)画一画见详解;(2)否;(3)12平方厘米
【分析】(1)平移图形的画法:首先在原图形上选择几个关键点,例如此题中的顶点;然后按照要求将这些点向规定的方向平移指定的格数,保持这些点的相对位置不变是很重要的。接下来连接对应的点,形成平移后的图形;据此可解此题。
(2)根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此可解此题。
(3)根据小方格边长为1厘米,则1个小方格的面积为1平方厘米,数一数,可以发现组成后图形是由10个完整的小方格以及4个一半的方格组成,4个一半的方格也就是2个完整的小方格,所以围成的总面积为12平方厘米,据此可解此题。
【详解】(1)画一画如图:
(2)观察图形可知,以a为对称轴,图形①平移后的图形与图形②组成的图形不是轴对称图形。
(3)根据分析可知,图形①平移后的图形与图形②组成的图形的面积是12平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考重点专题:平面图形-2023-2024学年数学六年级下册北师大版
一、选择题
1.下面几幅图中,三角形被遮住了一部分,不能直接确定三角形种类的是( )。
A. B.
C. D.
2.某市计划扩建一个长方形绿化带,若长增加12米,宽不变,面积就增加144平方米;若宽增加8米,长不变,面积也增加144平方米。这个绿化带原来的面积是( )平方米。
A.96 B.104 C.124 D.216
3.如图,用两个完全一样的等腰梯形拼成一个平行四边形,每个梯形的周长是( )厘米。
A.35 B.50 C.55 D.70
4.一个圆柱的高与底面直径相等,将圆柱的侧面沿高剪开,得到的长方形的长和宽的比是( )。
A.1∶1 B.π∶1 C.1∶π D.1∶2
5.长方形的长和宽都扩大2倍,它的面积扩大( )倍。
A.2 B.4 C.8 D.10
6.一个钟表的分钟长10厘米,从3时走到5时,分针尖端走过来( )厘米。
A.31.4 B.62.8 C.125.6 D.50.24
二、填空题
7.王师傅想要加工一个三角形自行车支架,两根钢管的长度分别是6分米和5分米,第三根最短( )分米,最长( )分米(取整分米数)。支架做成三角形的依据是( )。
8.一个平行四边形相邻两边的长度是5厘米和8厘米,平行四边形的周长是( )厘米。
9.一个等腰梯形周长是60厘米,上底是7厘米,下底是9厘米,腰长是( )厘米。
10.一块长方形绿地宽9米,面积是450平方米,如果宽增加到36米,而长不变,扩大后的长方形绿地的面积是( )平方米。
11.甲圆的半径等于乙圆的直径,则甲圆和乙圆面积的比是( )∶( )。
12.一个圆形花坛的半径是12米,将它改造成一个正方形花坛,但不改变花坛的周长,则正方形花坛的边长是( )米。
三、判断题
13.下图中,a∥b,三个图形的面积相等。( )
14.如图平行四边形的面积一定小于50平方厘米。( )
15.一个梯形的高不变,上底增加4cm,下底减少4cm,它的面积与原来的面积相等。( )
16.在同一个圆中,扇形的大小与圆心角的度数无关。( )
17.一个圆的半径扩大到原来的2倍,周长也扩大到原来的2倍。( )
四、计算题
18.分别求出阴影部分的周长和面积。(单位:cm)
19.求图中阴影部分的面积。
20.如图,两个相同的半圆叠拼放置,求阴影部分的面积。(单位:厘米)
五、解答题
21.小明的爸爸在郊区租了一块长方形菜地。长是12.8米,宽是长的。这块长方形菜地的占地面积是多少平方米?
22.如图,王爷爷准备在这块地中圈出一个最大的正方形种植韭菜,其余的地方种植菠菜。请在图上画出你的设计方案,并算出韭菜地和菠菜地的面积。
23.在比例尺为1∶200的地图上,小明家的客厅长为3厘米,宽为2厘米,爸爸在装修时想用一种浅白色的方砖铺地面,经询问商店,这种方砖铺18平方米需要618块,那么请你计算一下,在不浪费的情况下,爸爸买多少块这种方砖正好够用?
24.如图,一个正六边形的边长和一个小圆的周长相等。如果这个小圆按箭头方向从某一位置沿着正六边形的周边做无滑动滚动,直至回到原出发位置。那么
(1)这个小圆滚动了多少圈?
(2)这个小圆回到原出发位置经过部分的面积是多少平方厘米?(小圆的半径为1厘米,π取3.14,结果保留两位小数。)
25.先按要求画一画,再回答问题(设小方格边长为1厘米)。
(1)将图形①先向右平移4格,再向下平移5格。
(2)以虚线a为对称轴,图形①平移后的图形与图形②组成的图形是否为轴对称图形?( )(填“是”或“否”)
(3)图形①平移后的图形与图形②组成的图形的面积是( )。
参考答案:
1.B
【分析】有一个角是钝角的三角形是钝角三角形,三个角都是锐角的三角形是锐角三角形,有一个角是直角的三角形是直角三角形;依此即可选择。
【详解】
A.此三角形漏出的角为钝角,因此这是一个钝角三角形。
B.、、此幅图中的三角形可能是直角三角形,也可能是锐角三角形,还可能是钝角三角形。
C.此三角形漏出的角为直角,因此这是一个直角三角形。
D.此三角形是一个锐角三角形。
由此可知,不能直接确定三角形种类的是。
故答案为:B
2.D
【分析】根据长方形的面积=长×宽,用增加的面积除以增加的宽求出原来的长,用增加的面积除以增加的长求出原来的宽,然后把数据代入公式即可;据此解答。
【详解】根据分析:
(144÷8)×(144÷12)
=18×12
=216(平方米)
所以这个绿化带原来的面积是216平方米。
故答案为:D
3.B
【分析】观察上图可知,等腰梯形的腰长为15厘米,梯形的上底加下底的和为20厘米,等腰梯形的周长=上底+下底+腰长×2,把数据代入计算即可解答。
【详解】20+15×2
=20+30
=50(厘米)
每个梯形的周长是50厘米。
故答案为:B
4.B
【分析】已知圆柱的侧面展开图一般是长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高;
根据比的意义写出长方形的长和宽的比,即圆柱的底面周长与高的比,已知圆柱的高与底面直径相等,据此化简比即可。
【详解】圆柱的高与底面直径相等,即h=d。
长方形的长∶宽
=圆柱的底面周长∶高
=πd∶h
=πd∶d
=π∶1
得到的长方形的长和宽的比是π∶1。
故答案为:B
5.B
【分析】长方形的面积=长×宽,积的变化规律:一个因数不变,另一个因数乘(或除以)几(0除外),积也乘(或除以)几;那么长方形的长和宽都扩大2倍,它的面积会扩大(2×2)倍;据此解答。
【详解】根据分析:2×2=4,所以长方形的长和宽都扩大2倍,它的面积扩大4倍。
故答案为:B
6.C
【分析】1小时分针绕钟面旋转一周,分针从3时走到5时,分针绕钟面旋转两周,分钟长10厘米作圆的半径,根据圆的周长:C=2πr,求出分针绕钟面旋转一周分针尖端走过的路程,最后乘2即可。
【详解】10×2×3.14×2
=62.8×2
=125.6(厘米)
从3时走到5时,分针尖端走过来125.6厘米。
故答案为:C
7. 2 10 三角形具有稳定性
【分析】三角形具有稳定性,三角形的稳定性在实际生活中有很多应用,如相机三脚架。任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边。第三根钢管最短是(6-5+1)分米,最长是(6+5-1)分米。
【详解】6+5-1
=11-1
=10(分米)
6-5+1
=1+1
=2(分米)
王师傅想要加工一个三角形自行车支架,两根钢管的长度分别是6分米和5分米,第三根最短2分米,最长10分米,分米(取整分米数)。支架做成三角形的依据是三角形具有稳定性。
8.26
【分析】两组对边分别平行且相等的四边形,叫做平行四边形;根据平行四边形相邻两边的长度是5厘米和8厘米可知,另外两条边的长度也是5厘米和8厘米,把平行四边形4条边长度相加,即可求出平行四边形周长。
【详解】5+8+5+8=26(厘米)
即一个平行四边形相邻两边的长度是5厘米和8厘米,平行四边形的周长是26厘米。
9.22
【分析】结合等腰梯形的特征可知,等腰梯形的两腰相等。根据梯形的周长可知,用梯形周长减去其上下底之和,再除以2就是其腰长。
【详解】(60-7-9)÷2
=44÷2
=22(厘米)
其腰长为22厘米。
10.1800
【分析】先根据长方形的长=面积÷宽,求出绿地的长。再根据长方形的面积=长×宽,求出扩大后的绿地面积。
【详解】450÷9×36
=50×36
=1800(平方米)
扩大后的长方形绿地的面积是1800平方米。
11. 4 1
【分析】假设甲圆的半径是2,那么乙圆的直径是2,半径是1。根据圆的面积公式S=πr2先分别求出两个圆的面积,再求出甲圆和乙圆面积的比即可。
【详解】令甲圆半径是2,则乙圆直径是2,
2÷2=1
3.14×22
=3.14×4
=12.56
3.14×12
=3.14×1
=3.14
12.56∶3.14=(12.56÷3.14)∶(3.14÷3.14)=4∶1
所以,甲圆和乙圆面积的比是4∶1。
12.18.84
【分析】已知圆形花坛的半径是12米,根据圆的周长公式C=2πr,求出圆形花坛的周长;
将它改造成一个正方形花坛,但不改变花坛的周长,即正方形的周长等于圆的周长;根据正方形的边长=周长÷4,即可求出正方形花坛的边长。
【详解】圆的周长:
2×3.14×12=75.36(米)
正方形的边长:
75.36÷4=18.84(米)
则正方形花坛的边长是18.84米。
13.×
【分析】平行线间的距离处处相等,也就是三个图形的高都是相等的,平行四边形的面积=底×高,三角形的面积=底×高÷2,梯形的面积=(上底+下底)×高÷2,假设高是1,代入数据计算出三个图形的面积作对比即可求解。
【详解】平行四边形面积=4×1=4(cm2)
三角形面积=4×1÷2=2(cm2)
梯形的面积=(3+1)×1÷2=4×1÷2=2(cm2)
三个图形的面积不相等,原题说法错误。
故答案为:×
14.√
【分析】如下图,作出平行四边形的底10厘米对应的高h,由“直角三角形中斜边最长”可知,h小于5厘米;根据平行四边形的面积=底×高,得出平行四边形的面积与50平方厘米的大小关系。
【详解】如图:
h<5
10×h<10×5,即10h<50;
所以,平行四边形的面积一定小于50平方厘米。
原题说法正确。
故答案为:√
15.√
【分析】根据梯形的面积=(上底+下底)×高÷2可知,梯形的高不变,上底增加4cm,下底减少4cm,则上底与下底之和不变,所以梯形的面积不变。
【详解】原来梯形的面积=(上底+下底)×高÷2
现在梯形的高不变,上底增加4cm,下底减少4cm,则梯形的面积是:
(上底+4+下底-4)×高÷2=(上底+下底)×高÷2
它的面积与原来的面积相等。
原题说法正确。
故答案为:√
16.×
【分析】在同一个圆中,扇形的与扇形对应的圆心角度数密切相关,根据圆心角与扇形面积的关系,可以做出判断。
【详解】在同一个圆中,扇形的大小与这个扇形的圆心角大小有关,圆心角越大扇形越大,圆心角越小扇形越小,所以原题说法错误。
故答案为:×
17.√
【分析】圆周长=2πr,据此通过举例子的方式来判断题干的正误。
【详解】例:一个圆的半径是1,周长为2×π×1=2π。当半径扩大到原来的2倍,变成2,此时周长为2×π×2=4π。4π÷2π=2,所以周长也扩大到原来的2倍。
所以,一个圆的半径扩大到原来的2倍,周长也扩大到原来的2倍。
故答案为:√
18.周长:23.98cm;面积:10.99cm2
【分析】阴影部分周长等于半径是4cm圆的周长的一半+半径是(4-1)cm圆的周长的一半+1×2,根据圆的周长公式:周长=π×半径×2,代入数据,求出阴影部分周长;
阴影部分面积=圆环面积的一半,根据圆环面积公式:面积=π×(大圆半径2-小圆半径2),代入数据,求出圆环面积,再除以2,即可解答。
【详解】3.14×4×2÷2+3.14×(4-1)×2÷2+1×2
=12.56×2÷2+3.14×3×2÷2+2
=12.56+9.42+2
=23.98(cm)
3.14×(42-32)÷2
=3.14×(16-9)÷2
=3.14×7÷2
=21.98÷2
=10.99(cm2)
阴影周长是23.98cm,面积是10.99cm2。
19.6cm2
【分析】阴影部分面积=半径是2cm的圆的半圆面积+上底是4cm,下底是6cm,高是2cm的梯形面积-底是4cm,高是2cm的三角形面积-半径是2cm半圆的面积,由此可知,阴影部分面积=梯形面积-三角形面积,根据梯形面积公式:面积=(上底+下底)×高÷2,三角形面积公式:面积=底×高÷2,代入数据,即可解答。
【详解】(4+6)×2÷2-4×2÷2
=10×2÷2-8÷2
=20÷2-4
=10-4
=6(cm2)
20.41.04平方厘米
【分析】
如图:,4个阴影部分的面积相等,2个阴影部分面积等于半径是(12÷2)厘米的半圆面积减去底是12厘米,高是(12÷2)厘米的三角形面积,根据圆的面积公式:面积=π×半径×半径,三角形面积公式:面积=底×高÷2,代入数据,求出2个阴影部分面积,再乘2,即可解答。
【详解】3.14×(12÷2)2÷2-12×(12÷2)÷2
=3.14×62÷2-12×6÷2
=3.14×36÷2-72÷2
=113.04÷2-36
=56.52-36
=20.52(平方厘米)
20.52×2=41.04(平方厘米)
阴影部分面积是41.04平方厘米。
21.122.88平方米
【分析】先把长方形的长看作单位“1”,已知宽是长的,根据求一个数的几分之几是多少,用乘法计算,求出长方形的宽;
再根据长方形的面积=长×宽,求出这块长方形菜地的面积。
【详解】宽:12.8×=9.6(米)
面积:12.8×9.6=122.88(平方米)
答:这块长方形菜地的占地面积是122.88平方米。
22.设计方案见详解;韭菜地面积:3600平方米;菠菜地面积:1800平方米
【分析】正方形四条边相等,要将长方形围成一个最大的正方形,那么以长方形的宽作为正方形的边长,从长方形的长上取60米的长度,与宽围成一个边长为60米的正方形,这个正方形最大;然后根据正方形的面积=边长×边长,长方形的面积=长×宽;据此计算各自的面积。
【详解】设计方案如下:
韭菜地面积:60×60=3600(平方米)
菠菜地面积:(90-60)×60
=30×60
=1800(平方米)
答:韭菜地的面积为3600平方米,菠菜地的面积为1800平方米。
23.824块
【分析】根据实际距离=图上距离÷比例尺,换算出客厅实际长和宽,长方形面积=长×宽,据此求出客厅面积,铺的面积÷用的方砖块数=每块方砖面积,客厅面积÷每块方砖面积=方砖块数,据此列式解答。
【详解】3÷=3×200=600(厘米)=6(米)
2÷=2×200=400(厘米)=4(米)
6×4÷(18÷618)
=24÷
=24×
=824(块)
答:爸爸买824块这种方砖正好够用。
24.(1)7圈;
(2)87.92平方厘米
【分析】(1)小圆在滚动的过程中,除了要滚正六边形的边,还要滚动正六边形的六个角。因为正六边形的边长和一个小圆的周长相等,则小圆滚动六条边正好是六圈。滚动整个六边形是360°,则每个顶点是滚动60°,即每个顶点滚动了圈,6个顶点就是1个圈。加上滚动边的6圈,合在一起是7圈。
(2)每个顶点滚动了圈,是以顶点为圆心,小圆的直径为半径的的圆,则每个顶点经过的面积=,且半径是小圆的直径。小圆滚过每条边形成了一个长方形,这个长方形的长是小圆的周长,宽是小圆的直径。再根据长方形的面积=长×宽得出小圆的经过每条边的面积,再乘6就是6条边经过的面积。最后相加即可。
【详解】(1)360°÷6=60°
(圈)
=
(圈)
答:这个小圆滚动了7圈。
(2)
=
(平方厘米)
(平方厘米)
=
(平方厘米)
(平方厘米)
(平方厘米)
28×3.14=87.92(平方厘米)
答:这个小圆回到原出发位置经过部分的面积是87.92平方厘米。
25.(1)画一画见详解;(2)否;(3)12平方厘米
【分析】(1)平移图形的画法:首先在原图形上选择几个关键点,例如此题中的顶点;然后按照要求将这些点向规定的方向平移指定的格数,保持这些点的相对位置不变是很重要的。接下来连接对应的点,形成平移后的图形;据此可解此题。
(2)根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;据此可解此题。
(3)根据小方格边长为1厘米,则1个小方格的面积为1平方厘米,数一数,可以发现组成后图形是由10个完整的小方格以及4个一半的方格组成,4个一半的方格也就是2个完整的小方格,所以围成的总面积为12平方厘米,据此可解此题。
【详解】(1)画一画如图:
(2)观察图形可知,以a为对称轴,图形①平移后的图形与图形②组成的图形不是轴对称图形。
(3)根据分析可知,图形①平移后的图形与图形②组成的图形的面积是12平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
