第十章 数据的收集、整理与描述课时同步练习 2023—2024学年人教版数学七年级下册
文档属性
| 名称 | 第十章 数据的收集、整理与描述课时同步练习 2023—2024学年人教版数学七年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 00:00:00 | ||
图片预览




文档简介
第十章 数据的收集、整理与描述
10.1 统计调查
基础知识夯实
中小学教育资源及组卷应用平台
知识沉淀
1.统计调查的方法有 和 .
(1)全面调查:考察 的调查.
(2)抽样调查:只抽取 对象进行的调查叫做抽样调查,抽样调查中,抽取的样本必须具有代表性.
2.抽样调查
抽样调查中的总体:所要考察对象的 ;
个体:其中 考察对象;
样本:从总体中取出的一部分个体;
样本容量:样本中个体的 .
基础过关
1.下列事件中,最适合采用全面调查的是 ( )
A.对某班全体学生出生月份的调查
B.对全国中学生节水意识的调查
C.对某批次灯泡使用寿命的调查
D.对山西省初中学生每天阅读时间的调查
2.如图,扇形 A 表示地球陆地面积占全球面积的百分比,则此扇形的圆心角为 度.
3.某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有5 件不合格,那么 你估计 该 厂 这 20 万件产 品 中 合 格 品 约为 .
典型案例探究
知识点 1 全面调查与抽样调查的有关概念
【例题1】(1)下列调查中,适合采用抽样调查的是( )
A.调查本市非毕业年级学生对“社团课”的满意程度
B.调查本班同学的身高
C.为保证某种新研发的战斗机成功试飞,对其零部件进行检查
D.对乘坐高铁的乘客进行安检
(2)去年某校有1 000名考生参加中考,为了了解这些考生的数学成绩,从中抽取 100 名考生的数学成绩进行统计分析,以下说法错误的是 ( )
A.这100名考生的数学成绩是总体的一个样本
B.这 1 000名考生的数学成绩是总体
C.每位考生的数学成绩是个体
D.100名学生是样本容量
【变式1】(1)在“生命安全”主题教育活动中,为了解甲、乙两所学校学生对生命安全知识掌握情况,小安同学制定了如下方案,你认为最合理的是 ( )
A.抽取甲校初二年级学生进行调查
B.在乙校随机抽取 200名学生进行调查
C.随机抽取甲、乙两所学校100名老师进行调查
D.在甲、乙两所学校各随机抽取100 名学生进行调查
(2)为了了解某校2 000名学生的身高情况,随机抽取了该校200名学生测量身高,在这个问题中,
总体是 ;
个体是 ;
样本是 ;
样本容量是 .
知识点 2 用统计图表描述数据
【例题2】学习统计知识后,小兵就本班同学的上学方式进行调查统计,如图是通过收集数据后绘制的两幅不完整的统计图.
请根据图中提供的信息解答下列问题:
(1)该班共有 名学生;
(2)将表示“步行”部分的条形统计图补充完整;
(3)在扇形统计图中,“骑车”部分扇形所对的圆心角是 度;
(4)若全年级共有 1 000 名学生,估计全年级步行上学的学生有多少人
【变式2】某中学为了解九年级学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图.
(1)这次抽样调查的样本容量是 ,并补全条形图;
(2)D 等级学生人数占被调查人数的百分比为 ,在扇形统计图中C等级所对应的圆心角为 ;
(3)该校九年级学生有1 500 人,请你估计其中 A等级的学生人数.
课后作业
A 组
1.下列调查中,最适合采用全面调查方式的是 ( )
A.对某市居民日平均用水量的调查
B.对一批LED节能灯使用寿命的调查
C.对某新闻频道某栏目收视率的调查
D.对某校九年级(1)班同学的身高情况的调查
2.要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是 ( )
A.调查全体女生
B.调查全体男生
C.调查七年级全体学生
D.调查七、八、九年级各 100 名学生
3.2018年的世界无烟日期间,某学习小组为了解本地区大约有多少成年人吸烟,随机调查了 100 个成年人,结果其中20 个成年人吸烟,对于这个关于数据收集与处理的问题,下列说法正确的是 ( )
A.调查的方式是全面调查
B.本地区约有 20%的成年人吸烟
C.样本是20个吸烟的成年人
D.本地区只有80个成年人不吸烟
4.为了解某校2 000 名学生的视力情况,随机抽取了该校100名学生的视力情况.在这个问题中,样本容量是 ( )
A.2 000名学生 B.2 000
C.100名学生 D.100
5.某校团委为了解本校八年级500 名学生的睡眠时间,随机选择了该年级 100名学生进行调查.关于下列说法:
①本次调查方式属于抽样调查;
②总体是全校学生的睡眠时间;
③100名学生的睡眠时间是总体的一个样本;
④个体是100名学生的睡眠时间.
其中正确的是 ( )
A.①③ B.①④ C.②③ D.②④
6.为了解某校七年级同学的视力情况,从中随机抽查了30名学生的视力.在这个问题中,样本是
7.一个扇形统计图中,某部分所对应的圆心角为36°,则该部分占总体的百分比是 .
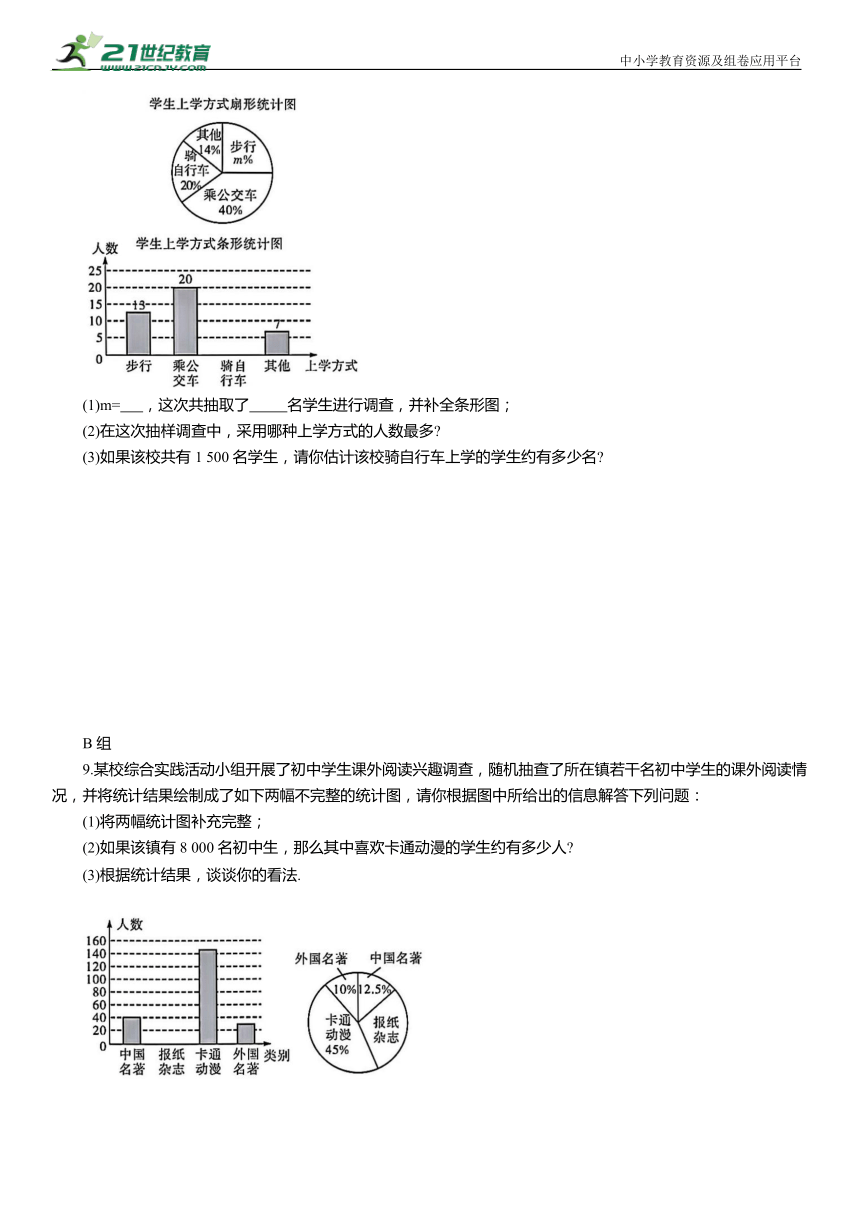
8.省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动.某中学为了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图),请根据图中提供的信息,解答下列问题.
(1)m= ,这次共抽取了 名学生进行调查,并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多
(3)如果该校共有 1 500 名学生,请你估计该校骑自行车上学的学生约有多少名
B 组
9.某校综合实践活动小组开展了初中学生课外阅读兴趣调查,随机抽查了所在镇若干名初中学生的课外阅读情况,并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给出的信息解答下列问题:
(1)将两幅统计图补充完整;
(2)如果该镇有 8 000 名初中生,那么其中喜欢卡通动漫的学生约有多少人
(3)根据统计结果,谈谈你的看法.
10.“戒烟一小时,健康亿人行”.2018年国际无烟日,小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:A.顾客出面制止;B.劝说进吸烟室;C.餐厅老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图,请你根据图中的信息回答下列问题.
(1)这次抽样的公众有 人;
(2)请将统计图(1)补充完整;
(3)在统计图(2)中,“无所谓”部分所对应的圆心角是 °;
(4)若城区人口有20万人,估计赞成“餐厅老板出面制止”的有 万人,并根据统计信息,谈谈自己的感想.(不超过30个字)
10.2 直方图
基础知识夯实
知识沉淀
1.直方图的相关概念:
(1)组距:把所有数据分成若干组,每个小组的两个端点之间的距离(组内数据的取值范围).
(2)频数:落在各个小组内的数据的个数.
(3)频数分布直方图:以小长方形的面积来反映数据在各个小组内的频数的大小.
2.画频数分布直方图的一般步骤:
(1)计算 与 的差;
(2)决定 与组数;
(3)列 表;
(4)画频数分布直方图.
基础过关
1.将100个数据分成①~⑧组,如下表:
组号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
频数 4 8 12 24 18 7 3
那么第④组的频数为 ( )
A.24 B.26 C.0.24 D.0.26
2.一个样本含有下面 10 个数据:52,51,49,50,47,48,50,51,48,53,则最大的值是 ,最小的值是 ,如果组距为1.5,则应该分成 组.
典型案例探究
知识点 1 组距和组数
【例题1】有40个数据,其中最大值为35,最小值为14,若取组距为4,则应该分的组数是 ( )
A.4 B.5 C.6 D.7
知识点 2 频数分布直方图
【例题2】为了解七年级学生的数学成绩,随机抽查 30名学生的数学成绩,制作了频数分布直方图如图所示,根据图示解答:
(1)组距是 ,组数是 ;
(2)第三组的频数是 ,频率是 ;
(3)若七年级有学生 600人,请估计80 分以上有多少人.
【变式1】已知一组数据,最大值是 93,最小值为 22,现要把它分成6组,则下列组距最合适的是 ( )
A.9 B.12 C.15 D.18
【变式2】某校为了解九年级学生的体能情况,随机抽查了其中40名学生,测试了他们做1m in仰卧起坐的次数,并制成了如图所示的频数分布直方图,根据图示解答:
(1)组距是 ,组数 ;
(2)第二组的频数是 ,频率是 ;
(3)若九年级有学生800人,请估计1min做仰卧起坐 25次以下的人数.
课后作业
A 组
1.已知一组数据有80个,其中最大值为140,最小值为40.取组距为10,则可以分成 ( )
A.10组 B.9组 C.8组 D.7 组
2.在对n个数据整理时,把这些数据分成7组,则各组的频数之和、频率之和分别为 ( )
A. n和1 B. n和n C.1和n D.1 和1
3.一组数据共 50个,分别落在5 个小组内,第一、二、三、四小组的数据个数分别为2,8,15,20,则第五个小组的频数和频率分别为 、 .
4.某班学生参加十九大知识竞赛,将竞赛所取得的成绩(得分取整数)进行整理后分成5组,并绘制成频数分布直方图(如图),请回答下列问题.
(1)该班共有多少名学生
(2)60.5~70.5 这一分数段的频数、频率分别是多少
5.根据某班40名同学的体重频数分布直方图,回答下列问题:
(1)体重在哪个范围内的人数最多
(2)体重超过 59.5 kg 的同学占全班同学的百分之几
6.某校八年级学生进行体育测试,八年级(2)班男生的立定跳远成绩绘制成如图所示的频数分布直方图,图中从左到右各矩形的高之比是2:3:7 :5 :3,最后一组的频数是6,根据直方图所表达的信息,解答下列问题.
(1)该班有多少名男生
(2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格,则该班男生的这项测试合格率是多少
7.为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得的数据整理后,画出频数分布直方图(如图).
(1)求抽取了多少名男生测量身高.
(2)身高在哪个范围内的男生人数最多
(3)若该中学有300 名男生,请你估计身高为 170厘米及170厘米以上的人数.
B 组
8.为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,绘成统计图表:
身高分组 频数 百分比
x<155 5 10%
155≤x<160 a 20%
160≤x<165 15 30%
165≤x<170 14 b
x≥170 6 12%
总计 100%
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
(3)该校九年级共有 600 名学生,估计身高不低于165 cm的学生有 人.
9.在某校“情系灾区,爱心相助”捐款活动中,某班50名学生捐款数如下(单位:元):
19 20 25 30 28 27 26 21 20 22
24 23 25 29 27 88 27 30 19 20
5 10030 45 32 57 68 40 12 30
22 48 59 90 100 3028 25 39 10
55 12 21 30 40 50 50 10 101100
班主任老师准备将这组数据制成频数分布直方图,以表彰他们的爱心.制图时必须先计算出最大值与最小值的差为 ;若取组距为10,则应分成 组;若第一组的起点定为4.5,则在24.5~34.5范围内的频数是 ,请列出频数分布表并画出频数分布直方图.
10.3 课题学习 从数据谈节水(略)
章末整合·感知中考
知识网络
内容归纳
1.全面调查:考察全体对象的调查叫做全面调查.
2.抽样调查:抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况称为抽样调查.
3.总体:要考察的全体对象称为总体.
4.个体:组成总体的每一个考察对象称为个体.
5.样本:被抽取的所有个体构成总体的一个样本.
6.样本容量:样本中包含的个体的数目称为样本容量.
7.频数:一般地,我们称落在不同小组中的数据个数为该组的频数.
8.频率:频数与数据总数的比为频率.
9.组数和组距:在统计数据时,把数据按照一定的范围分成若干各组,分成组的个数称为组数,每个小组两个端点之间的距离称为组距.
中考完全接触
知识点一 全面调查与抽样调查
1.以下调查中,适宜全面调查的是( )
A.调查某批次汽车的抗撞击能力
B.调查某班学生的身高情况
C.调查春节联欢晚会的收视率
D.调查济宁市居民日平均用水量
2.下列调查适合采用抽样调查的是( )
A.某公司招聘人员,对应聘人员进行面试
B.调查一批节能灯泡的使用寿命
C.为保证火箭的成功发射,对其零部件进行检查
D.对乘坐某次航班的乘客进行安全检查
3.下列采用的调查方式中,合适的是( )
A.为了解东江湖的水质情况,采用抽样调查的方式
B.某企业为了解所生产的产品的合格率,采用全面调查的方式
C.某小型企业给在职员工做工作服前进行尺寸大小的调查,采用抽样调查的方式
D.某市教育部门为了解该市中小学生的视力情况,采用全面调查的方式
4.某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:
①从扇形图中分析出最受学生欢迎的种类;
②去图书馆收集学生借阅图书的记录;
③绘制扇形图来表示各个种类所占的百分比;
④整理借阅图书记录并绘制频数分布表;
正确统计步骤的顺序是 ( )
A.②→③→①→④ B.③→④→①→②
C.①→②→④→③ D.②→④→③→①
知识点二 折线图、条形图、扇形图
5.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )
A.签约金额逐年增加
B.与上年相比,2019年的签约金额的增长量最多
C.签约金额的年增长速度最快的是2016 年
D.2018年的签约金额比2017年降低了22.98%
6.如图所示,是巴中某校对学生到校方式的情况统计图.若该校骑自行车到校的学生有200人,则步行到校的学生有 ( )
A.120人 B.160人 C.125 人 D.180人
7.要表示一个家庭一年用于“教育、服装、食品、其他”这四项的支出各占家庭本年总支出的百分比,从“扇形统计图、条形统计图、折线统计图”中选择一种统计图,最适合的是 .
8.某市对九年级学生进行“综合素质”评价,评价结果分为 A,B,C,D,E五个等级.现随机抽取了500名学生的评价结果作为样本进行分析,绘制了如图所示的统计图.已知图中从左到右的五个长方形的高之比为2:3:3:1 :1,据此估算该市80 000名九年级学生中“综合素质”评价结果为“A”的学生约为 人.
9.我市“创建文明城市”活动正如火如荼的展开.某校为了做好“创文”活动的宣传,就本校学生对“创文”有关知识进行测试,然后随机抽取了部分学生的测试成绩进行统计分析,并将分析结果绘制成如下两幅不完整的统计图:
各等级学生人数条形统计图 各等级学生人数扇形统计图
若该校有学生2 000人,请根据以上统计结果估计成绩为优秀和良好的学生共有 人.
10.董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况,他们绘制了两幅不完整的统计图(A.小于 5 天;B.5天;C.6天;D.7天),则扇形统计图 B 部分所对应的圆心角的 度数是 .
11为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查.整理样本数据,得到下表:
视力 4.7 以下 4.7 4.8 4.9 4.9以上
人数 102 98 80 93 127
根据抽样调查结果,估计该区12 000名初中学生中视力不低于4.8的人数是 .
12.某校学生自主建立了一个学习用品义卖平台,已知九年级 200 名学生义卖所得金额的频数分布直方图如图所示,那么20~30元这个小组的频率是 .
13.某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(80分及以上)的学生有 人.
知识点四 数据的收集、整理与描述的综合应用
14为了解某校九年级全体男生1 000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制如下不完整的统计图表,根据图表信息解答问题:
x = ,y = ,扇形图中表示C的圆心角的度数为 .
成绩等级频数分布表
成绩等级 频数
A 24
B 10
C x
D 2
合计 y
成绩等级扇形统计图
15.为了解朝阳社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
(1)求参与问卷调查的总人数;
(2)补全条形统计图;
(3)该社区中20~60岁的居民约8 000人,估算这些人中最喜欢微信支付方式的人数.
16.为弘扬中华优秀传统文化,某校开展了“经典雅韵”诵读比赛活动,现随机抽取部分同学的成绩进行统计,并绘制如下两幅不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整;
(2)求扇形 B的圆心角度数;
(3)如果全校有 2 000 名学生参加这次活动,90 分以上(含90分)为优秀,那么估计获得优秀的学生有多少人
17.为了增强学生的安全意识,某校组织了一次全校 2 500 名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了 100 份考卷进行分析统计,发现考试成绩(x分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.
分数段/分 频数/人 频率
51≤x<61 a 0.1
61≤x<71 18 0.18
71≤x<81 b n
81≤x<91 35 0.35
91≤x<101 12 0.12
合计 100 1
请根据图表提供的信息,解答下列问题:
(1)填空:a= ,n= ,b= ;
(2)将频数分布直方图补充完整;
(3)该校对考试成绩为91≤x≤100的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数. 10.1 统计调查
【基础知识夯实】
知识沉淀
1.全面调查 抽样调查
(1)全体对象
(2)一部分
2.全体 每一个数目
基础过关
1. A 2.108 3.19万件
【典型案例探究】
例题1 (1)A (2)D
变式1 (1)D (2)略
例题 2 (1)40 (2)略 (3)108 (4)200
变式2 (1)50,图略 (2)8% 72° (3)480
【课后作业】
1. D 2. D 3. B 4. D 5. A
6.30名学生的视力 7.10%
8.解:(1)26 50 条形图如图所示:
(2)采用乘公交车上学的人数最多.
(3)该校骑自行车上学的人数约为1 500×20%=300(人).
9.(1)略 (2)3 600 (3)略
10.(1)200 (2)略 (3)18 (4)6.感想略.
10.2 直方图
【基础知识夯实】
知识沉淀
2.(1)最大值 最小值 (2)组距
(3)频数分布
基础过关
1. A 2.53 47 4
【典型案例探究】
例题1 C
变式1 B
例题 2 (1)10 6 (2)6 20% (3)200
变式2 (1)5 5 (2)10 25% (3)260
【课后作业】
1. A 2. A 3.5 0.1
4.解:(1)3+12+18+9+6=48(名).
(2)频数是12,频率是
5.(1)49.5~54.5kg (2)17.5%
6.(1)40名 (2)75%
7.(1)50名 (2)165~170c m (3)108
8.(1)10 28% (2)略 (3)240
9.96 10 17 列表画图略
10.3 课题学习 从数据谈节水(略)
章末整合·感知中考
【中考完全接触】
1. B 2. B 3. A 4. D 5. C 6. B
7.扇形统计图 8.16 000 9.1 400
10.108° 11.7 200 12.0.25 13.90
14.4 40 36°
15.(1)500 (2)图略 (3)2 800
16.(1)30,图略(2)50.4° (3)400人
17.(1)10 25 0.25 (2)图略 (3)90人
10.1 统计调查
基础知识夯实
中小学教育资源及组卷应用平台
知识沉淀
1.统计调查的方法有 和 .
(1)全面调查:考察 的调查.
(2)抽样调查:只抽取 对象进行的调查叫做抽样调查,抽样调查中,抽取的样本必须具有代表性.
2.抽样调查
抽样调查中的总体:所要考察对象的 ;
个体:其中 考察对象;
样本:从总体中取出的一部分个体;
样本容量:样本中个体的 .
基础过关
1.下列事件中,最适合采用全面调查的是 ( )
A.对某班全体学生出生月份的调查
B.对全国中学生节水意识的调查
C.对某批次灯泡使用寿命的调查
D.对山西省初中学生每天阅读时间的调查
2.如图,扇形 A 表示地球陆地面积占全球面积的百分比,则此扇形的圆心角为 度.
3.某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检,发现其中有5 件不合格,那么 你估计 该 厂 这 20 万件产 品 中 合 格 品 约为 .
典型案例探究
知识点 1 全面调查与抽样调查的有关概念
【例题1】(1)下列调查中,适合采用抽样调查的是( )
A.调查本市非毕业年级学生对“社团课”的满意程度
B.调查本班同学的身高
C.为保证某种新研发的战斗机成功试飞,对其零部件进行检查
D.对乘坐高铁的乘客进行安检
(2)去年某校有1 000名考生参加中考,为了了解这些考生的数学成绩,从中抽取 100 名考生的数学成绩进行统计分析,以下说法错误的是 ( )
A.这100名考生的数学成绩是总体的一个样本
B.这 1 000名考生的数学成绩是总体
C.每位考生的数学成绩是个体
D.100名学生是样本容量
【变式1】(1)在“生命安全”主题教育活动中,为了解甲、乙两所学校学生对生命安全知识掌握情况,小安同学制定了如下方案,你认为最合理的是 ( )
A.抽取甲校初二年级学生进行调查
B.在乙校随机抽取 200名学生进行调查
C.随机抽取甲、乙两所学校100名老师进行调查
D.在甲、乙两所学校各随机抽取100 名学生进行调查
(2)为了了解某校2 000名学生的身高情况,随机抽取了该校200名学生测量身高,在这个问题中,
总体是 ;
个体是 ;
样本是 ;
样本容量是 .
知识点 2 用统计图表描述数据
【例题2】学习统计知识后,小兵就本班同学的上学方式进行调查统计,如图是通过收集数据后绘制的两幅不完整的统计图.
请根据图中提供的信息解答下列问题:
(1)该班共有 名学生;
(2)将表示“步行”部分的条形统计图补充完整;
(3)在扇形统计图中,“骑车”部分扇形所对的圆心角是 度;
(4)若全年级共有 1 000 名学生,估计全年级步行上学的学生有多少人
【变式2】某中学为了解九年级学生的体能状况,从九年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图.
(1)这次抽样调查的样本容量是 ,并补全条形图;
(2)D 等级学生人数占被调查人数的百分比为 ,在扇形统计图中C等级所对应的圆心角为 ;
(3)该校九年级学生有1 500 人,请你估计其中 A等级的学生人数.
课后作业
A 组
1.下列调查中,最适合采用全面调查方式的是 ( )
A.对某市居民日平均用水量的调查
B.对一批LED节能灯使用寿命的调查
C.对某新闻频道某栏目收视率的调查
D.对某校九年级(1)班同学的身高情况的调查
2.要了解全校学生的课外作业负担情况,你认为以下抽样方法中比较合理的是 ( )
A.调查全体女生
B.调查全体男生
C.调查七年级全体学生
D.调查七、八、九年级各 100 名学生
3.2018年的世界无烟日期间,某学习小组为了解本地区大约有多少成年人吸烟,随机调查了 100 个成年人,结果其中20 个成年人吸烟,对于这个关于数据收集与处理的问题,下列说法正确的是 ( )
A.调查的方式是全面调查
B.本地区约有 20%的成年人吸烟
C.样本是20个吸烟的成年人
D.本地区只有80个成年人不吸烟
4.为了解某校2 000 名学生的视力情况,随机抽取了该校100名学生的视力情况.在这个问题中,样本容量是 ( )
A.2 000名学生 B.2 000
C.100名学生 D.100
5.某校团委为了解本校八年级500 名学生的睡眠时间,随机选择了该年级 100名学生进行调查.关于下列说法:
①本次调查方式属于抽样调查;
②总体是全校学生的睡眠时间;
③100名学生的睡眠时间是总体的一个样本;
④个体是100名学生的睡眠时间.
其中正确的是 ( )
A.①③ B.①④ C.②③ D.②④
6.为了解某校七年级同学的视力情况,从中随机抽查了30名学生的视力.在这个问题中,样本是
7.一个扇形统计图中,某部分所对应的圆心角为36°,则该部分占总体的百分比是 .
8.省教育厅决定在全省中小学开展“关注校车、关爱学生”为主题的交通安全教育宣传周活动.某中学为了解本校学生的上学方式,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图(如图),请根据图中提供的信息,解答下列问题.
(1)m= ,这次共抽取了 名学生进行调查,并补全条形图;
(2)在这次抽样调查中,采用哪种上学方式的人数最多
(3)如果该校共有 1 500 名学生,请你估计该校骑自行车上学的学生约有多少名
B 组
9.某校综合实践活动小组开展了初中学生课外阅读兴趣调查,随机抽查了所在镇若干名初中学生的课外阅读情况,并将统计结果绘制成了如下两幅不完整的统计图,请你根据图中所给出的信息解答下列问题:
(1)将两幅统计图补充完整;
(2)如果该镇有 8 000 名初中生,那么其中喜欢卡通动漫的学生约有多少人
(3)根据统计结果,谈谈你的看法.
10.“戒烟一小时,健康亿人行”.2018年国际无烟日,小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:A.顾客出面制止;B.劝说进吸烟室;C.餐厅老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图,请你根据图中的信息回答下列问题.
(1)这次抽样的公众有 人;
(2)请将统计图(1)补充完整;
(3)在统计图(2)中,“无所谓”部分所对应的圆心角是 °;
(4)若城区人口有20万人,估计赞成“餐厅老板出面制止”的有 万人,并根据统计信息,谈谈自己的感想.(不超过30个字)
10.2 直方图
基础知识夯实
知识沉淀
1.直方图的相关概念:
(1)组距:把所有数据分成若干组,每个小组的两个端点之间的距离(组内数据的取值范围).
(2)频数:落在各个小组内的数据的个数.
(3)频数分布直方图:以小长方形的面积来反映数据在各个小组内的频数的大小.
2.画频数分布直方图的一般步骤:
(1)计算 与 的差;
(2)决定 与组数;
(3)列 表;
(4)画频数分布直方图.
基础过关
1.将100个数据分成①~⑧组,如下表:
组号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧
频数 4 8 12 24 18 7 3
那么第④组的频数为 ( )
A.24 B.26 C.0.24 D.0.26
2.一个样本含有下面 10 个数据:52,51,49,50,47,48,50,51,48,53,则最大的值是 ,最小的值是 ,如果组距为1.5,则应该分成 组.
典型案例探究
知识点 1 组距和组数
【例题1】有40个数据,其中最大值为35,最小值为14,若取组距为4,则应该分的组数是 ( )
A.4 B.5 C.6 D.7
知识点 2 频数分布直方图
【例题2】为了解七年级学生的数学成绩,随机抽查 30名学生的数学成绩,制作了频数分布直方图如图所示,根据图示解答:
(1)组距是 ,组数是 ;
(2)第三组的频数是 ,频率是 ;
(3)若七年级有学生 600人,请估计80 分以上有多少人.
【变式1】已知一组数据,最大值是 93,最小值为 22,现要把它分成6组,则下列组距最合适的是 ( )
A.9 B.12 C.15 D.18
【变式2】某校为了解九年级学生的体能情况,随机抽查了其中40名学生,测试了他们做1m in仰卧起坐的次数,并制成了如图所示的频数分布直方图,根据图示解答:
(1)组距是 ,组数 ;
(2)第二组的频数是 ,频率是 ;
(3)若九年级有学生800人,请估计1min做仰卧起坐 25次以下的人数.
课后作业
A 组
1.已知一组数据有80个,其中最大值为140,最小值为40.取组距为10,则可以分成 ( )
A.10组 B.9组 C.8组 D.7 组
2.在对n个数据整理时,把这些数据分成7组,则各组的频数之和、频率之和分别为 ( )
A. n和1 B. n和n C.1和n D.1 和1
3.一组数据共 50个,分别落在5 个小组内,第一、二、三、四小组的数据个数分别为2,8,15,20,则第五个小组的频数和频率分别为 、 .
4.某班学生参加十九大知识竞赛,将竞赛所取得的成绩(得分取整数)进行整理后分成5组,并绘制成频数分布直方图(如图),请回答下列问题.
(1)该班共有多少名学生
(2)60.5~70.5 这一分数段的频数、频率分别是多少
5.根据某班40名同学的体重频数分布直方图,回答下列问题:
(1)体重在哪个范围内的人数最多
(2)体重超过 59.5 kg 的同学占全班同学的百分之几
6.某校八年级学生进行体育测试,八年级(2)班男生的立定跳远成绩绘制成如图所示的频数分布直方图,图中从左到右各矩形的高之比是2:3:7 :5 :3,最后一组的频数是6,根据直方图所表达的信息,解答下列问题.
(1)该班有多少名男生
(2)若立定跳远的成绩在2.0米以上(包括2.0米)为合格,则该班男生的这项测试合格率是多少
7.为了解某中学男生的身高情况,随机抽取若干名男生进行身高测量,将所得的数据整理后,画出频数分布直方图(如图).
(1)求抽取了多少名男生测量身高.
(2)身高在哪个范围内的男生人数最多
(3)若该中学有300 名男生,请你估计身高为 170厘米及170厘米以上的人数.
B 组
8.为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,绘成统计图表:
身高分组 频数 百分比
x<155 5 10%
155≤x<160 a 20%
160≤x<165 15 30%
165≤x<170 14 b
x≥170 6 12%
总计 100%
(1)填空:a= ,b= ;
(2)补全频数分布直方图;
(3)该校九年级共有 600 名学生,估计身高不低于165 cm的学生有 人.
9.在某校“情系灾区,爱心相助”捐款活动中,某班50名学生捐款数如下(单位:元):
19 20 25 30 28 27 26 21 20 22
24 23 25 29 27 88 27 30 19 20
5 10030 45 32 57 68 40 12 30
22 48 59 90 100 3028 25 39 10
55 12 21 30 40 50 50 10 101100
班主任老师准备将这组数据制成频数分布直方图,以表彰他们的爱心.制图时必须先计算出最大值与最小值的差为 ;若取组距为10,则应分成 组;若第一组的起点定为4.5,则在24.5~34.5范围内的频数是 ,请列出频数分布表并画出频数分布直方图.
10.3 课题学习 从数据谈节水(略)
章末整合·感知中考
知识网络
内容归纳
1.全面调查:考察全体对象的调查叫做全面调查.
2.抽样调查:抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况称为抽样调查.
3.总体:要考察的全体对象称为总体.
4.个体:组成总体的每一个考察对象称为个体.
5.样本:被抽取的所有个体构成总体的一个样本.
6.样本容量:样本中包含的个体的数目称为样本容量.
7.频数:一般地,我们称落在不同小组中的数据个数为该组的频数.
8.频率:频数与数据总数的比为频率.
9.组数和组距:在统计数据时,把数据按照一定的范围分成若干各组,分成组的个数称为组数,每个小组两个端点之间的距离称为组距.
中考完全接触
知识点一 全面调查与抽样调查
1.以下调查中,适宜全面调查的是( )
A.调查某批次汽车的抗撞击能力
B.调查某班学生的身高情况
C.调查春节联欢晚会的收视率
D.调查济宁市居民日平均用水量
2.下列调查适合采用抽样调查的是( )
A.某公司招聘人员,对应聘人员进行面试
B.调查一批节能灯泡的使用寿命
C.为保证火箭的成功发射,对其零部件进行检查
D.对乘坐某次航班的乘客进行安全检查
3.下列采用的调查方式中,合适的是( )
A.为了解东江湖的水质情况,采用抽样调查的方式
B.某企业为了解所生产的产品的合格率,采用全面调查的方式
C.某小型企业给在职员工做工作服前进行尺寸大小的调查,采用抽样调查的方式
D.某市教育部门为了解该市中小学生的视力情况,采用全面调查的方式
4.某同学要统计本校图书馆最受学生欢迎的图书种类,以下是排乱的统计步骤:
①从扇形图中分析出最受学生欢迎的种类;
②去图书馆收集学生借阅图书的记录;
③绘制扇形图来表示各个种类所占的百分比;
④整理借阅图书记录并绘制频数分布表;
正确统计步骤的顺序是 ( )
A.②→③→①→④ B.③→④→①→②
C.①→②→④→③ D.②→④→③→①
知识点二 折线图、条形图、扇形图
5.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )
A.签约金额逐年增加
B.与上年相比,2019年的签约金额的增长量最多
C.签约金额的年增长速度最快的是2016 年
D.2018年的签约金额比2017年降低了22.98%
6.如图所示,是巴中某校对学生到校方式的情况统计图.若该校骑自行车到校的学生有200人,则步行到校的学生有 ( )
A.120人 B.160人 C.125 人 D.180人
7.要表示一个家庭一年用于“教育、服装、食品、其他”这四项的支出各占家庭本年总支出的百分比,从“扇形统计图、条形统计图、折线统计图”中选择一种统计图,最适合的是 .
8.某市对九年级学生进行“综合素质”评价,评价结果分为 A,B,C,D,E五个等级.现随机抽取了500名学生的评价结果作为样本进行分析,绘制了如图所示的统计图.已知图中从左到右的五个长方形的高之比为2:3:3:1 :1,据此估算该市80 000名九年级学生中“综合素质”评价结果为“A”的学生约为 人.
9.我市“创建文明城市”活动正如火如荼的展开.某校为了做好“创文”活动的宣传,就本校学生对“创文”有关知识进行测试,然后随机抽取了部分学生的测试成绩进行统计分析,并将分析结果绘制成如下两幅不完整的统计图:
各等级学生人数条形统计图 各等级学生人数扇形统计图
若该校有学生2 000人,请根据以上统计结果估计成绩为优秀和良好的学生共有 人.
10.董永社区在创建全国卫生城市的活动中,随机检查了本社区部分住户五月份某周内“垃圾分类”的实施情况,他们绘制了两幅不完整的统计图(A.小于 5 天;B.5天;C.6天;D.7天),则扇形统计图 B 部分所对应的圆心角的 度数是 .
11为了了解某区初中学生的视力情况,随机抽取了该区500名初中学生进行调查.整理样本数据,得到下表:
视力 4.7 以下 4.7 4.8 4.9 4.9以上
人数 102 98 80 93 127
根据抽样调查结果,估计该区12 000名初中学生中视力不低于4.8的人数是 .
12.某校学生自主建立了一个学习用品义卖平台,已知九年级 200 名学生义卖所得金额的频数分布直方图如图所示,那么20~30元这个小组的频率是 .
13.某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(80分及以上)的学生有 人.
知识点四 数据的收集、整理与描述的综合应用
14为了解某校九年级全体男生1 000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为A、B、C、D四个等级,绘制如下不完整的统计图表,根据图表信息解答问题:
x = ,y = ,扇形图中表示C的圆心角的度数为 .
成绩等级频数分布表
成绩等级 频数
A 24
B 10
C x
D 2
合计 y
成绩等级扇形统计图
15.为了解朝阳社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
(1)求参与问卷调查的总人数;
(2)补全条形统计图;
(3)该社区中20~60岁的居民约8 000人,估算这些人中最喜欢微信支付方式的人数.
16.为弘扬中华优秀传统文化,某校开展了“经典雅韵”诵读比赛活动,现随机抽取部分同学的成绩进行统计,并绘制如下两幅不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整;
(2)求扇形 B的圆心角度数;
(3)如果全校有 2 000 名学生参加这次活动,90 分以上(含90分)为优秀,那么估计获得优秀的学生有多少人
17.为了增强学生的安全意识,某校组织了一次全校 2 500 名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了 100 份考卷进行分析统计,发现考试成绩(x分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.
分数段/分 频数/人 频率
51≤x<61 a 0.1
61≤x<71 18 0.18
71≤x<81 b n
81≤x<91 35 0.35
91≤x<101 12 0.12
合计 100 1
请根据图表提供的信息,解答下列问题:
(1)填空:a= ,n= ,b= ;
(2)将频数分布直方图补充完整;
(3)该校对考试成绩为91≤x≤100的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数. 10.1 统计调查
【基础知识夯实】
知识沉淀
1.全面调查 抽样调查
(1)全体对象
(2)一部分
2.全体 每一个数目
基础过关
1. A 2.108 3.19万件
【典型案例探究】
例题1 (1)A (2)D
变式1 (1)D (2)略
例题 2 (1)40 (2)略 (3)108 (4)200
变式2 (1)50,图略 (2)8% 72° (3)480
【课后作业】
1. D 2. D 3. B 4. D 5. A
6.30名学生的视力 7.10%
8.解:(1)26 50 条形图如图所示:
(2)采用乘公交车上学的人数最多.
(3)该校骑自行车上学的人数约为1 500×20%=300(人).
9.(1)略 (2)3 600 (3)略
10.(1)200 (2)略 (3)18 (4)6.感想略.
10.2 直方图
【基础知识夯实】
知识沉淀
2.(1)最大值 最小值 (2)组距
(3)频数分布
基础过关
1. A 2.53 47 4
【典型案例探究】
例题1 C
变式1 B
例题 2 (1)10 6 (2)6 20% (3)200
变式2 (1)5 5 (2)10 25% (3)260
【课后作业】
1. A 2. A 3.5 0.1
4.解:(1)3+12+18+9+6=48(名).
(2)频数是12,频率是
5.(1)49.5~54.5kg (2)17.5%
6.(1)40名 (2)75%
7.(1)50名 (2)165~170c m (3)108
8.(1)10 28% (2)略 (3)240
9.96 10 17 列表画图略
10.3 课题学习 从数据谈节水(略)
章末整合·感知中考
【中考完全接触】
1. B 2. B 3. A 4. D 5. C 6. B
7.扇形统计图 8.16 000 9.1 400
10.108° 11.7 200 12.0.25 13.90
14.4 40 36°
15.(1)500 (2)图略 (3)2 800
16.(1)30,图略(2)50.4° (3)400人
17.(1)10 25 0.25 (2)图略 (3)90人
