第五章 相交线与平行线课时强化训练(含答案)
文档属性
| 名称 | 第五章 相交线与平行线课时强化训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 00:00:00 | ||
图片预览


文档简介
第五章 相交线与平行线课时强化训练
5.1 相交线
第1 课时 相交线
1.下列说法正确的是 ( )
A.大小相等的两个角互为对顶角
B.有公共顶点且相等的两个角是对顶角
C.两角之和为180°,则这两个角互为邻补角
D.一个角的邻补角可能是锐角、钝角或直角
2.已知∠α=m°,则∠α的对顶角为 °,∠α的邻补角为 °.
3.如图,直线 l ,l 和 l 相交构成8个角,已知∠1=∠5,∠5 的对顶角是 ,与∠5相等的角有∠1, ;∠5的邻补角是 ,与∠5互补的角有 .
4.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC,∠BOE的邻补角;
(2)写出∠DOA,∠EOC的对顶角;
(3)如果∠AOC=50°,求∠BOD,∠COB 的度数.
5.如图,已知直线 AB,CD 交于点O,OE 平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
6.直线AB,CD 相交于点O,OE,OF是两条射线.
(1)如图(1),若∠EOF=90°,且OD平分∠AOE,∠BOF=60°,求∠AOD的度数;
(2)如图(2),若OE平分∠BOD,∠AOC=68°,∠DOF=90°,求∠EOF 的度数;
(3)如图(3),若OF 平分∠COE,∠BOF=15°,若设∠AOE=x,求∠AOC的度数.(用含x的式子表示)
中小学教育资源及组卷应用平台
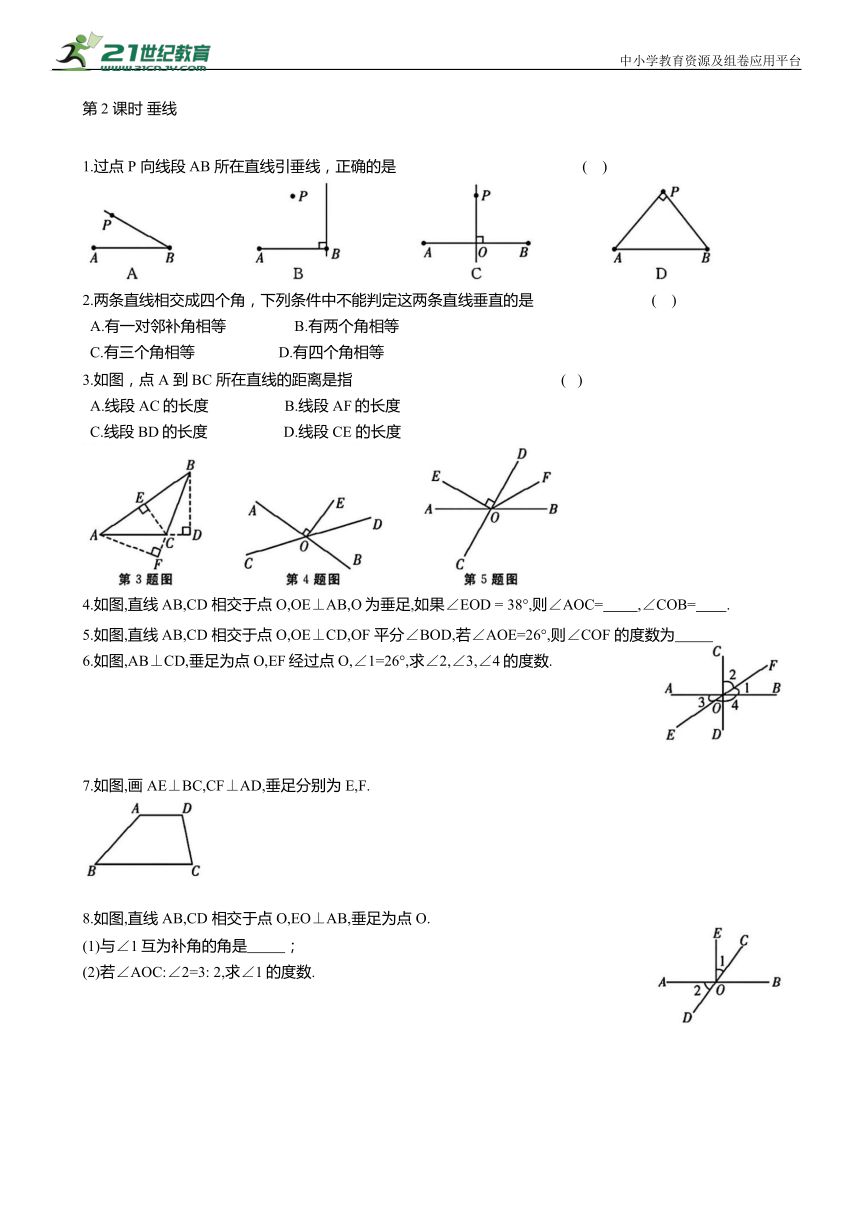
第2 课时 垂线
1.过点 P 向线段AB 所在直线引垂线,正确的是 ( )
2.两条直线相交成四个角,下列条件中不能判定这两条直线垂直的是 ( )
A.有一对邻补角相等 B.有两个角相等
C.有三个角相等 D.有四个角相等
3.如图,点 A 到BC 所在直线的距离是指 ( )
A.线段 AC的长度 B.线段 AF的长度
C.线段 BD的长度 D.线段 CE 的长度
4.如图,直线AB,CD 相交于点O,OE⊥AB,O为垂足,如果∠EOD = 38°,则∠AOC= ,∠COB= .
5.如图,直线AB,CD 相交于点O,OE⊥CD,OF 平分∠BOD,若∠AOE=26°,则∠COF 的度数为
6.如图,AB⊥CD,垂足为点O,EF经过点O,∠1=26°,求∠2,∠3,∠4的度数.
7.如图,画AE⊥BC,CF⊥AD,垂足分别为E,F.
8.如图,直线 AB,CD 相交于点O,EO⊥AB,垂足为点 O.
(1)与∠1互为补角的角是 ;
(2)若∠AOC:∠2=3: 2,求∠1的度数.
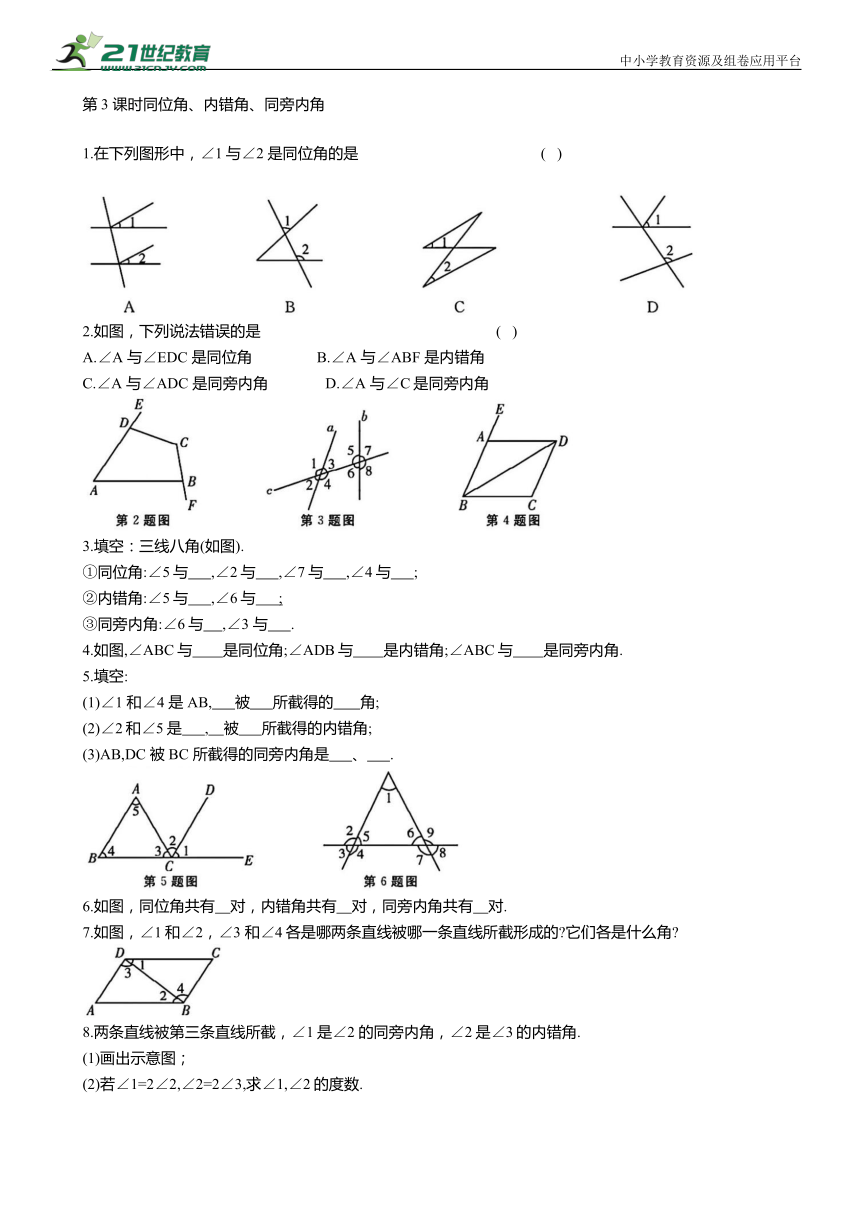
第3 课时同位角、内错角、同旁内角
1.在下列图形中,∠1与∠2 是同位角的是 ( )
2.如图,下列说法错误的是 ( )
A.∠A 与∠EDC 是同位角 B.∠A 与∠ABF 是内错角
C.∠A 与∠ADC 是同旁内角 D.∠A 与∠C是同旁内角
3.填空:三线八角(如图).
①同位角:∠5与 ,∠2与 ,∠7与 ,∠4与 ;
②内错角:∠5与 ,∠6与 ;
③同旁内角:∠6与 ,∠3 与 .
4.如图,∠ABC与 是同位角;∠ADB与 是内错角;∠ABC与 是同旁内角.
5.填空:
(1)∠1 和∠4 是 AB, 被 所截得的 角;
(2)∠2和∠5是 , 被 所截得的内错角;
(3)AB,DC 被BC 所截得的同旁内角是 、 .
6.如图,同位角共有 对,内错角共有 对,同旁内角共有 对.
7.如图,∠1和∠2,∠3 和∠4各是哪两条直线被哪一条直线所截形成的 它们各是什么角
8.两条直线被第三条直线所截,∠1是∠2 的同旁内角,∠2是∠3的内错角.
(1)画出示意图;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2的度数.
5.2 平行线及其判定
第 1 课时 平行线
1.下列说法正确的是 ( )
A.经过一点有且只有一条直线与已知直线平行
B.经过一点有无数条直线与已知直线平行
C.经过一点至少有一条直线与已知直线平行
D.经过直线外一点有且只有一条直线与这条直线平行
2.在同一平面内,直线a与b相交于点M,a∥c,那么b与c 的关系是 ( )
A. 平行 B. 相交 C.平行与相交 D.不能确定
3.如图,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是 ( )
A.平行 B.垂直
C.平行或垂直 D.无法确定
4.在同一平面内,三条直线的交点个数可能是 .
5.如图,在直角梯形ABCD中,相互平行的直线有 对,相互垂直的直线有 对.
6.如图,已知直线 MN的同侧有三个点A,B,C,且AB∥MN,BC∥MN,试说明A,B,C三点在同一直线上.
7.已知:P是∠AOB 内部的一点.过点 P 画OA 的平行线交OB 于点C,过点 P 画OB 的平行线交OA于点 D.
8.画图题:
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段 AB的垂线GH 和平行线EF;
(2)判断EF,GH的位置关系;
(3)连接AC和BC,求三角形ABC的面积.
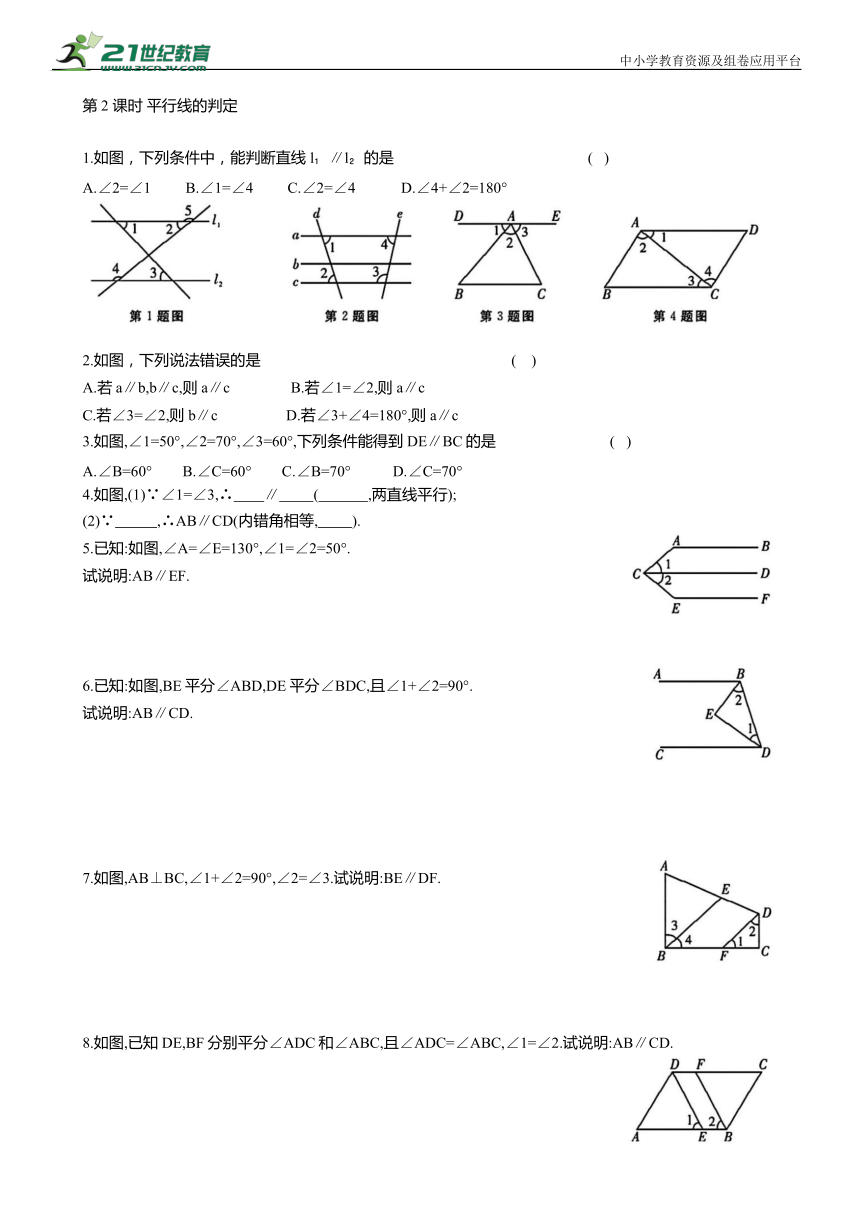
第2 课时 平行线的判定
1.如图,下列条件中,能判断直线l ∥l 的是 ( )
A.∠2=∠1 B.∠1=∠4 C.∠2=∠4 D.∠4+∠2=180°
2.如图,下列说法错误的是 ( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠4=180°,则a∥c
3.如图,∠1=50°,∠2=70°,∠3=60°,下列条件能得到 DE∥BC的是 ( )
A.∠B=60° B.∠C=60° C.∠B=70° D.∠C=70°
4.如图,(1)∵∠1=∠3,∴ ∥ ( ,两直线平行);
(2)∵ ,∴AB∥CD(内错角相等, ).
5.已知:如图,∠A=∠E=130°,∠1=∠2=50°.
试说明:AB∥EF.
6.已知:如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.
试说明:AB∥CD.
7.如图,AB⊥BC,∠1+∠2=90°,∠2=∠3.试说明:BE∥DF.
8.如图,已知DE,BF分别平分∠ADC和∠ABC,且∠ADC=∠ABC,∠1=∠2.试说明:AB∥CD.
5.3 平行线的性质
第 1 课时平行线的性质
1.如图,已知a∥b,∠1=55°,则∠2 的度数是 ( )
A.35° B.45° C.55° D.125°
2.如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为 ( )
A.10° B.15° C.20° D.25°
3.如图,已知AB∥CD,直线EF分别交AB,CD 于点E,F,EG平分∠BEF,若∠1=50°,则∠2的度数是 ( )
A.70° B.65° C.60° D.50°
4.如图,已知∠1=∠2,∠3=73°,则∠4的度数为 .
5.如图,点D,E分别在AB,BC上,DE∥AC,AF∥BC,∠1=70°,则∠2= .
6.如图,AD∥BC,∠D=100°,CA平分∠BCD,则∠DAC= .
7.如图,BC⊥AE,垂足为点C,过点C作CD∥AB.若∠ECD=48°,则∠B= .
8.如图,直线a∥b,AB⊥BC,如果∠1=60°,那么∠2= .
9.如图,AB∥CD,∠ABD和∠BDC的平分线交于点E,BE交CD 于点F.
(1)试说明:∠1+∠2=90°;
(2)若∠3=50°,求∠2的度数.
10.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
第2课时 平行线的判定与性质的综合运用
1.如图,∠1+∠2=180°,∠3=108°,则∠4的度数是 ( )
A.72° B.80° C.82° B.108°
2.如图,若∠A+∠ABC=180°,则下列结论正确的是 ( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠2=∠4
3.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD= .
4.如图,若∠A=∠F,∠C=∠D,则BD平行于CE 吗 说说你的理由.
5.如图,A,B,C三点在同一直线上,∠1 =∠2 ,∠3 =∠D,试说明:BD∥CE.
6.如图, 试说明:AM∥CN.
7.如图, ,BE平分
(1)AD 与BC 平行吗 请说明理由.
(2)AB 与EF 的位置关系如何 为什么
(3)若AF平分∠BAD,试说明:
第3课时 命题、定理、证明
1.下列语句中,不是命题的是 ( )
A.内错角相等 B.如果a+b=0,那么a,b互为相反数
C.已知 求 a的值 D.这件衣服是红色的
2.下列命题是假命题的是 ( )
A.等角的补角相等 B.内错角相等 C.两点之间,线段最短D.两点确定一条直线( )
3.如图,下列推理及所注明的理由都正确的是( )
A.因为DE∥BC,所以∠1=∠C(同位角相等,两直线平行)
B.因为∠2=∠3,所以DE∥BC(两直线平行,内错角相等)
C.因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等)
D.因为∠1=∠C,所以 DE∥BC(两直线平行,同位角相等)
4.“两数之和始终是正数”是 命题.
5.把命题“平行于同一条直线的两条直线互相平行”改写成“如果……那么……”的形式为 .
6.如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1 和∠2,则∠1+∠2= 度.
7.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有 (只填序号).
8.已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题有 (填写所有真命题的序号).
9.已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断 BF 与AC 的位置关系,并说明理由.
10.如图1,已知MN∥PQ,A,B在MN上,C,D在PQ上,直线AD,BC交于点F.
(1)求证:∠PDF=∠F+∠ABC;
(2)如图2,DE 平分∠ADP,BE平分∠ABC,直线 DE,BE交于点E,请写出∠E 和∠F 的数量关系并说明理由.
5.4 平移
1.下列运动属于平移的是 ( )
A.荡秋千 B.地球绕着太阳转
C.风筝在空中随风飘动 D.急刹车时,汽车在地面上的滑动
2.下面的每组图形中,左边的平移后可以得到右边的是 ( )
3.如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,其平移的方法是 ( )
A.先向右平移3格,再向下平移4 格 B.先向右平移 2格,再向下平移3格
C.先向右平移4 格,再向下平移3 格 D.先向右平移3格,再向下平移2格
4.如图,多边形的相邻两边互相垂直,则这个多边形的周长为 ( )
A. a+b B.2a+b C.2a+2b D.2b+a
5.决定平移的基本要素是 和 .
6.如图,平移线段AB到CD 的位置,则AB= ,CD∥ ,BD= .
7.如图,在长方体中,平移后能得到棱 AA 的棱有 .
8.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动 格.
9.如图,边长为 4 cm的正方形 ABCD 先向上平移2cm,再向右平移1 cm,得到正方形. 此时阴影部分的面积为 .
10.现要把方格纸上的小船沿图中箭头方向平移8个单位长度,请你在方格纸上画出小船平移后的图形.
第五章复习题
1.如图,若∠1=70°,∠2=110°,∠3=70°,则有 ( )
A.a∥b B.c∥d
C. a⊥d D.任两条都无法判定是否平行
2.一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠1= ( )
A.18° B.54°
C.72° D.70°
3.在数学课上,同学们在练习过点 B 作线段AC 所在直线的垂线时,有一部分同学画出下列四种图形,请你数一数,错误的个数有
A.1个 B.2个 C.3个 D.4个
4.平面内三条直线的交点个数可能有 ( )
A.1个或3个 B.1个或2个或3 个
C.2个或3个 D.0个或1个或2个或3个
5.如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
解:∵ ∠1=∠2(已知),
∠1=∠3( ),
∴∠2=∠3(等量代换).
∴ ∥ ( ).
∴∠C=∠ABD( ).
又∵∠C=∠D(已知),
∴∠D=∠ABD( ).
∴AC∥DF( ).
6.如图,一块边长为30米的正方形土地,上面修了横竖各有两条道路,宽都是2米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积
7.如图,AE⊥BC,FG⊥BC,∠1=∠2.
(1)求证:AB∥CD;
(2)若∠D=∠3+50°,∠CBD=80°,求∠C的度数.
5.1 相交线
第 1 课时 相交线
1. D 2. m (180-m)
3.∠7 ∠3,∠7 ∠6,∠8 ∠2,∠4,∠6,∠8
4.解:(1)∠AOC的邻补角为∠COB,∠AOD.
∠BOE的邻补角为∠AOE,∠BOF.
(2)∠DOA 的对顶角为∠COB,∠EOC 的对顶角为∠FOD.
(3)∠BOD=50°,∠COB=130°.
5.解:可设∠2=x,则∠3=8x,x+x+8x=180°.
x=18°.∠AOC=∠BOD=36°.
6.解:(1)∵∠EOF=90°,∠BOF=60°,
∴∠BOE=90°—60°=30°.
∴∠AOE=180°—30°=150°.
∵OD平分∠AOE,
(2)∵∠AOC=68°,
∴∠BOD=∠AOC=68°.
∵OE 平分∠BOD,
∵∠DOF=90°,
∴∠EOF=90°-34°=56°.
(3)∵设∠AOE=x,
∴∠BOE=180°-x.
∴∠EOF=15°+180°-x=195°-x.
∵OF 平分∠COE,
∴∠COF=∠EOF=195°-x,
∴∠AOC=180°-(195°-x)-15°=x-30°.
第 2 课时 垂线
1. C 2. B 3. B 4.52° 128° 5.148°
6.∠2=64°,∠3=26°,∠4=154°
7.
8.解:(1)∠EOD
(2)∵∠AOC:∠2=3:2,
∴设∠AOC=3x,则∠2=2x.
故3x+2x=180°.
解得x=36°.则∠AOC=108°.
∵EO⊥AB,垂足为点O,
∴∠AOE=90°.
∴∠1=∠AOC-AOE=108°-90°=18°.
第3 课时 同位角、内错角、同旁内角1. B 2. D
3.①∠1 ∠6 ∠3 ∠8 ②∠4 ∠3 ③∠4 ∠5
4.∠EAD ∠CBD和∠EAD ∠BAD 和∠C
5.(1)DC BC 同位(2)AB DC AC
(3)∠4 ∠BCD
6.6 4 4
7.∠1和∠2 是 DC,AB 被BD 所截形成的内错角.∠3 和∠4 是 AD,BC被BD所截形成的内错角.
8.解:(1)如图所示.
(2)因为∠1=2∠2,∠2=2∠3,所以可设∠3=x,则∠2=2x,∠1=4x.
由图形可得∠1+∠3=180°,则x+4x=180°.
解得x=36°,
所以∠1=4×36°=144°,∠2=2×36°=72°.
5.2平行线及其判定
第 1课时 平行线
1. D2. B3. C
4.3.2,1,0
5.12
6.经过直线外一点,有且只有一条直线与这条直线平行
7.如图:
8.(1)如图.
(2)垂直
(3)10
第2课时 平行线的判定
1. D 2. C 3. B
4.(1)AD BC内错角相等
(2)∠2=∠4两直线平行
5.解:∵∠A=∠E=130°,∠1=∠2=50°,
∴∠A+∠1=130°+50°=180°,
∠E+∠2=130°+50°=180°.
∴AB∥CD,EF∥CD.
∴AB∥EF.
6.解:∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠2,∠BDC=2∠1.
∴∠ABD+∠BDC=2∠2+2∠1
=2(∠2+∠1)=2×90°=180°.
∴AB∥CD(同旁内角互补,两直线平行).
7.解:∵AB⊥BC,
∴∠ABC=90°,
即∠3+∠4=90°.
∴∠4=90°-∠3.
又∵∠1+∠2=90°,
∴∠1=90°-∠2.
又∵∠2=∠3,
∴∠4=∠1.∴BE∥DF.
解:∵DE平分∠ADC,BF平分∠ABC,
又∵∠ADC=∠ABC,
∵∠1=∠2,
∴∠CDE=∠1.
∴AB∥CD.
5.3 平行线的性质
第 1课时 平行线的性质
1. C 2. D 3. B
4.107° 5.70° 6.40° 7.42° 8.30°
9.解:(1)∵AB∥CD,
∴∠ABD+∠BDC=180°.
∵∠ABD和∠BDC的平分线交于点E,
∴∠ABD=2∠1,∠BDC=2∠2.
∴2∠1+2∠2=180°.
∴∠1+∠2=90°.
(2)∵AB∥CD,
∴∠3=∠ABF=50°.
∵BE是∠ABD的平分线,
10.解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴DG∥BA(内错角相等,两直线平行).
∴∠AGD+∠CAB=180°(两直线平行,同旁内角互补).
∵∠CAB=70°(已知),
∴∠AGD=110°(等式性质).
第2 课时平行线的判定与性质的综合运用
1. A 2. D 3.140°
4.解:BD∥CE.理由如下:
∵∠A=∠F.∴AC∥DF.
从而∠D=∠ABD.
∵∠C=∠D,
∴∠C=∠ABD,则BD∥CE.
5.解:∵∠1=∠2,
∴AD∥BE.
∴∠D=∠DBE.
∵∠3=∠D,
∴∠3=∠DBE,则 BD∥CE.
6.解:∵AB∥CD,
∴∠EAB=∠ECD.
∵∠1=∠2,
∴∠EAM=∠ECN.
∴AM∥CN.
7.解:(1)AD∥BC.理由如下:
∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF.∴AD∥BC.
(2)AB∥EF.理由如下:
∵BE平分∠ABC,∴∠ABC=2∠ABE.
又∠ABC=2∠E,∴∠ABE=∠E.
∴AB∥EF.
(3)∵AD∥BC,∴∠BAD+∠ABC=180°.
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE+∠BAF=90°.
由(2)得AB∥EF,
∴∠ABE=∠E,∠BAF=∠F.
∴∠E+∠F=90°.
第3课时命题、定理、证明
1. C 2. B 3. C
4.假
5.如果两条直线都和第三条直线平行,那么这两条直线也互相平行
6.90
7.①②③ 8.①②④
9.解:BF⊥AC.理由如下:
∵∠AGF=∠ABC,
∴BC∥GF(同位角相等,两直线平行).
∴∠1=∠3.
又∵∠1+∠2=180°,
∴∠2+∠3=180°.
∴BF∥DE.
∵DE⊥AC,
∴BF⊥AC.
10.(1)证明:∵MN∥PQ,∴∠DCF=∠ABC.
∵∠PDF+∠CDF=180°,∠F+∠DCF+∠CDF=180°,
∴∠PDF=∠F+∠DCF =∠F+∠ABC.
(2)解:
理由如下:
作 EG∥PQ,如图所示.
则EG∥MN∥PQ,
∴ ∠DCF = ∠ABC,∠DEG=∠PDE,∠BEG=∠MBE.
∴∠BED=∠DEG+∠BEG=∠PDE+∠MBE.
∵DE平分∠ADP,BE平分∠ABC,
又∠FDC=∠ADP,
又∠FDC+∠DCF=180°-∠F,
5.4 平移
1. D 2. D 3. B 4. C 5.平移方向平移距离
6. CD AB AC 7. BB ,CC ,DD 8.99.6 cm
10.解:将小船的各点沿箭头方向平移8格,得到对应点,顺次连接成新图即可.
所作图形如下:
第五章复习题
1. A 2. C 3. C 4. D
5.对顶角相等
CE BD 同位角相等,两直线平行
两直线平行,同位角相等
等量代换
内错角相等,两直线平行
6.解:30-2×2=26米,
26×26=676 平方米.
7.(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥FG.
∴∠1=∠CFG.
又∠1=∠2,
∴∠CFG=∠2.
∴AB∥CD.
(2)解:∵AB∥CD.
∴∠D+∠ABD=180°.
∴∠D+∠3+∠CBD=180°.
又∠D=∠3+50°,∠CBD=80°,
∴∠3=25°.
∵AB∥CD,
∴∠C=∠3=25°.
5.1 相交线
第1 课时 相交线
1.下列说法正确的是 ( )
A.大小相等的两个角互为对顶角
B.有公共顶点且相等的两个角是对顶角
C.两角之和为180°,则这两个角互为邻补角
D.一个角的邻补角可能是锐角、钝角或直角
2.已知∠α=m°,则∠α的对顶角为 °,∠α的邻补角为 °.
3.如图,直线 l ,l 和 l 相交构成8个角,已知∠1=∠5,∠5 的对顶角是 ,与∠5相等的角有∠1, ;∠5的邻补角是 ,与∠5互补的角有 .
4.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC,∠BOE的邻补角;
(2)写出∠DOA,∠EOC的对顶角;
(3)如果∠AOC=50°,求∠BOD,∠COB 的度数.
5.如图,已知直线 AB,CD 交于点O,OE 平分∠BOD,若∠3:∠2=8:1,求∠AOC的度数.
6.直线AB,CD 相交于点O,OE,OF是两条射线.
(1)如图(1),若∠EOF=90°,且OD平分∠AOE,∠BOF=60°,求∠AOD的度数;
(2)如图(2),若OE平分∠BOD,∠AOC=68°,∠DOF=90°,求∠EOF 的度数;
(3)如图(3),若OF 平分∠COE,∠BOF=15°,若设∠AOE=x,求∠AOC的度数.(用含x的式子表示)
中小学教育资源及组卷应用平台
第2 课时 垂线
1.过点 P 向线段AB 所在直线引垂线,正确的是 ( )
2.两条直线相交成四个角,下列条件中不能判定这两条直线垂直的是 ( )
A.有一对邻补角相等 B.有两个角相等
C.有三个角相等 D.有四个角相等
3.如图,点 A 到BC 所在直线的距离是指 ( )
A.线段 AC的长度 B.线段 AF的长度
C.线段 BD的长度 D.线段 CE 的长度
4.如图,直线AB,CD 相交于点O,OE⊥AB,O为垂足,如果∠EOD = 38°,则∠AOC= ,∠COB= .
5.如图,直线AB,CD 相交于点O,OE⊥CD,OF 平分∠BOD,若∠AOE=26°,则∠COF 的度数为
6.如图,AB⊥CD,垂足为点O,EF经过点O,∠1=26°,求∠2,∠3,∠4的度数.
7.如图,画AE⊥BC,CF⊥AD,垂足分别为E,F.
8.如图,直线 AB,CD 相交于点O,EO⊥AB,垂足为点 O.
(1)与∠1互为补角的角是 ;
(2)若∠AOC:∠2=3: 2,求∠1的度数.
第3 课时同位角、内错角、同旁内角
1.在下列图形中,∠1与∠2 是同位角的是 ( )
2.如图,下列说法错误的是 ( )
A.∠A 与∠EDC 是同位角 B.∠A 与∠ABF 是内错角
C.∠A 与∠ADC 是同旁内角 D.∠A 与∠C是同旁内角
3.填空:三线八角(如图).
①同位角:∠5与 ,∠2与 ,∠7与 ,∠4与 ;
②内错角:∠5与 ,∠6与 ;
③同旁内角:∠6与 ,∠3 与 .
4.如图,∠ABC与 是同位角;∠ADB与 是内错角;∠ABC与 是同旁内角.
5.填空:
(1)∠1 和∠4 是 AB, 被 所截得的 角;
(2)∠2和∠5是 , 被 所截得的内错角;
(3)AB,DC 被BC 所截得的同旁内角是 、 .
6.如图,同位角共有 对,内错角共有 对,同旁内角共有 对.
7.如图,∠1和∠2,∠3 和∠4各是哪两条直线被哪一条直线所截形成的 它们各是什么角
8.两条直线被第三条直线所截,∠1是∠2 的同旁内角,∠2是∠3的内错角.
(1)画出示意图;
(2)若∠1=2∠2,∠2=2∠3,求∠1,∠2的度数.
5.2 平行线及其判定
第 1 课时 平行线
1.下列说法正确的是 ( )
A.经过一点有且只有一条直线与已知直线平行
B.经过一点有无数条直线与已知直线平行
C.经过一点至少有一条直线与已知直线平行
D.经过直线外一点有且只有一条直线与这条直线平行
2.在同一平面内,直线a与b相交于点M,a∥c,那么b与c 的关系是 ( )
A. 平行 B. 相交 C.平行与相交 D.不能确定
3.如图,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是 ( )
A.平行 B.垂直
C.平行或垂直 D.无法确定
4.在同一平面内,三条直线的交点个数可能是 .
5.如图,在直角梯形ABCD中,相互平行的直线有 对,相互垂直的直线有 对.
6.如图,已知直线 MN的同侧有三个点A,B,C,且AB∥MN,BC∥MN,试说明A,B,C三点在同一直线上.
7.已知:P是∠AOB 内部的一点.过点 P 画OA 的平行线交OB 于点C,过点 P 画OB 的平行线交OA于点 D.
8.画图题:
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段 AB的垂线GH 和平行线EF;
(2)判断EF,GH的位置关系;
(3)连接AC和BC,求三角形ABC的面积.
第2 课时 平行线的判定
1.如图,下列条件中,能判断直线l ∥l 的是 ( )
A.∠2=∠1 B.∠1=∠4 C.∠2=∠4 D.∠4+∠2=180°
2.如图,下列说法错误的是 ( )
A.若a∥b,b∥c,则a∥c B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c D.若∠3+∠4=180°,则a∥c
3.如图,∠1=50°,∠2=70°,∠3=60°,下列条件能得到 DE∥BC的是 ( )
A.∠B=60° B.∠C=60° C.∠B=70° D.∠C=70°
4.如图,(1)∵∠1=∠3,∴ ∥ ( ,两直线平行);
(2)∵ ,∴AB∥CD(内错角相等, ).
5.已知:如图,∠A=∠E=130°,∠1=∠2=50°.
试说明:AB∥EF.
6.已知:如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.
试说明:AB∥CD.
7.如图,AB⊥BC,∠1+∠2=90°,∠2=∠3.试说明:BE∥DF.
8.如图,已知DE,BF分别平分∠ADC和∠ABC,且∠ADC=∠ABC,∠1=∠2.试说明:AB∥CD.
5.3 平行线的性质
第 1 课时平行线的性质
1.如图,已知a∥b,∠1=55°,则∠2 的度数是 ( )
A.35° B.45° C.55° D.125°
2.如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为 ( )
A.10° B.15° C.20° D.25°
3.如图,已知AB∥CD,直线EF分别交AB,CD 于点E,F,EG平分∠BEF,若∠1=50°,则∠2的度数是 ( )
A.70° B.65° C.60° D.50°
4.如图,已知∠1=∠2,∠3=73°,则∠4的度数为 .
5.如图,点D,E分别在AB,BC上,DE∥AC,AF∥BC,∠1=70°,则∠2= .
6.如图,AD∥BC,∠D=100°,CA平分∠BCD,则∠DAC= .
7.如图,BC⊥AE,垂足为点C,过点C作CD∥AB.若∠ECD=48°,则∠B= .
8.如图,直线a∥b,AB⊥BC,如果∠1=60°,那么∠2= .
9.如图,AB∥CD,∠ABD和∠BDC的平分线交于点E,BE交CD 于点F.
(1)试说明:∠1+∠2=90°;
(2)若∠3=50°,求∠2的度数.
10.如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
第2课时 平行线的判定与性质的综合运用
1.如图,∠1+∠2=180°,∠3=108°,则∠4的度数是 ( )
A.72° B.80° C.82° B.108°
2.如图,若∠A+∠ABC=180°,则下列结论正确的是 ( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠2=∠4
3.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD= .
4.如图,若∠A=∠F,∠C=∠D,则BD平行于CE 吗 说说你的理由.
5.如图,A,B,C三点在同一直线上,∠1 =∠2 ,∠3 =∠D,试说明:BD∥CE.
6.如图, 试说明:AM∥CN.
7.如图, ,BE平分
(1)AD 与BC 平行吗 请说明理由.
(2)AB 与EF 的位置关系如何 为什么
(3)若AF平分∠BAD,试说明:
第3课时 命题、定理、证明
1.下列语句中,不是命题的是 ( )
A.内错角相等 B.如果a+b=0,那么a,b互为相反数
C.已知 求 a的值 D.这件衣服是红色的
2.下列命题是假命题的是 ( )
A.等角的补角相等 B.内错角相等 C.两点之间,线段最短D.两点确定一条直线( )
3.如图,下列推理及所注明的理由都正确的是( )
A.因为DE∥BC,所以∠1=∠C(同位角相等,两直线平行)
B.因为∠2=∠3,所以DE∥BC(两直线平行,内错角相等)
C.因为DE∥BC,所以∠2=∠3(两直线平行,内错角相等)
D.因为∠1=∠C,所以 DE∥BC(两直线平行,同位角相等)
4.“两数之和始终是正数”是 命题.
5.把命题“平行于同一条直线的两条直线互相平行”改写成“如果……那么……”的形式为 .
6.如图,是我们生活中经常接触的小刀,刀片的外形是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1 和∠2,则∠1+∠2= 度.
7.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=40°,则下列结论:①∠BOE=70°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论有 (只填序号).
8.已知三条不同的直线a,b,c在同一平面内,下列四个命题:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中真命题有 (填写所有真命题的序号).
9.已知,如图,DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断 BF 与AC 的位置关系,并说明理由.
10.如图1,已知MN∥PQ,A,B在MN上,C,D在PQ上,直线AD,BC交于点F.
(1)求证:∠PDF=∠F+∠ABC;
(2)如图2,DE 平分∠ADP,BE平分∠ABC,直线 DE,BE交于点E,请写出∠E 和∠F 的数量关系并说明理由.
5.4 平移
1.下列运动属于平移的是 ( )
A.荡秋千 B.地球绕着太阳转
C.风筝在空中随风飘动 D.急刹车时,汽车在地面上的滑动
2.下面的每组图形中,左边的平移后可以得到右边的是 ( )
3.如图,在5×5方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,其平移的方法是 ( )
A.先向右平移3格,再向下平移4 格 B.先向右平移 2格,再向下平移3格
C.先向右平移4 格,再向下平移3 格 D.先向右平移3格,再向下平移2格
4.如图,多边形的相邻两边互相垂直,则这个多边形的周长为 ( )
A. a+b B.2a+b C.2a+2b D.2b+a
5.决定平移的基本要素是 和 .
6.如图,平移线段AB到CD 的位置,则AB= ,CD∥ ,BD= .
7.如图,在长方体中,平移后能得到棱 AA 的棱有 .
8.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动 格.
9.如图,边长为 4 cm的正方形 ABCD 先向上平移2cm,再向右平移1 cm,得到正方形. 此时阴影部分的面积为 .
10.现要把方格纸上的小船沿图中箭头方向平移8个单位长度,请你在方格纸上画出小船平移后的图形.
第五章复习题
1.如图,若∠1=70°,∠2=110°,∠3=70°,则有 ( )
A.a∥b B.c∥d
C. a⊥d D.任两条都无法判定是否平行
2.一副三角板按如图方式摆放,且∠1的度数比∠2的度数大54°,则∠1= ( )
A.18° B.54°
C.72° D.70°
3.在数学课上,同学们在练习过点 B 作线段AC 所在直线的垂线时,有一部分同学画出下列四种图形,请你数一数,错误的个数有
A.1个 B.2个 C.3个 D.4个
4.平面内三条直线的交点个数可能有 ( )
A.1个或3个 B.1个或2个或3 个
C.2个或3个 D.0个或1个或2个或3个
5.如图,E为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
解:∵ ∠1=∠2(已知),
∠1=∠3( ),
∴∠2=∠3(等量代换).
∴ ∥ ( ).
∴∠C=∠ABD( ).
又∵∠C=∠D(已知),
∴∠D=∠ABD( ).
∴AC∥DF( ).
6.如图,一块边长为30米的正方形土地,上面修了横竖各有两条道路,宽都是2米,空白的部分种上各种花草,请利用平移的知识求出种花草的面积
7.如图,AE⊥BC,FG⊥BC,∠1=∠2.
(1)求证:AB∥CD;
(2)若∠D=∠3+50°,∠CBD=80°,求∠C的度数.
5.1 相交线
第 1 课时 相交线
1. D 2. m (180-m)
3.∠7 ∠3,∠7 ∠6,∠8 ∠2,∠4,∠6,∠8
4.解:(1)∠AOC的邻补角为∠COB,∠AOD.
∠BOE的邻补角为∠AOE,∠BOF.
(2)∠DOA 的对顶角为∠COB,∠EOC 的对顶角为∠FOD.
(3)∠BOD=50°,∠COB=130°.
5.解:可设∠2=x,则∠3=8x,x+x+8x=180°.
x=18°.∠AOC=∠BOD=36°.
6.解:(1)∵∠EOF=90°,∠BOF=60°,
∴∠BOE=90°—60°=30°.
∴∠AOE=180°—30°=150°.
∵OD平分∠AOE,
(2)∵∠AOC=68°,
∴∠BOD=∠AOC=68°.
∵OE 平分∠BOD,
∵∠DOF=90°,
∴∠EOF=90°-34°=56°.
(3)∵设∠AOE=x,
∴∠BOE=180°-x.
∴∠EOF=15°+180°-x=195°-x.
∵OF 平分∠COE,
∴∠COF=∠EOF=195°-x,
∴∠AOC=180°-(195°-x)-15°=x-30°.
第 2 课时 垂线
1. C 2. B 3. B 4.52° 128° 5.148°
6.∠2=64°,∠3=26°,∠4=154°
7.
8.解:(1)∠EOD
(2)∵∠AOC:∠2=3:2,
∴设∠AOC=3x,则∠2=2x.
故3x+2x=180°.
解得x=36°.则∠AOC=108°.
∵EO⊥AB,垂足为点O,
∴∠AOE=90°.
∴∠1=∠AOC-AOE=108°-90°=18°.
第3 课时 同位角、内错角、同旁内角1. B 2. D
3.①∠1 ∠6 ∠3 ∠8 ②∠4 ∠3 ③∠4 ∠5
4.∠EAD ∠CBD和∠EAD ∠BAD 和∠C
5.(1)DC BC 同位(2)AB DC AC
(3)∠4 ∠BCD
6.6 4 4
7.∠1和∠2 是 DC,AB 被BD 所截形成的内错角.∠3 和∠4 是 AD,BC被BD所截形成的内错角.
8.解:(1)如图所示.
(2)因为∠1=2∠2,∠2=2∠3,所以可设∠3=x,则∠2=2x,∠1=4x.
由图形可得∠1+∠3=180°,则x+4x=180°.
解得x=36°,
所以∠1=4×36°=144°,∠2=2×36°=72°.
5.2平行线及其判定
第 1课时 平行线
1. D2. B3. C
4.3.2,1,0
5.12
6.经过直线外一点,有且只有一条直线与这条直线平行
7.如图:
8.(1)如图.
(2)垂直
(3)10
第2课时 平行线的判定
1. D 2. C 3. B
4.(1)AD BC内错角相等
(2)∠2=∠4两直线平行
5.解:∵∠A=∠E=130°,∠1=∠2=50°,
∴∠A+∠1=130°+50°=180°,
∠E+∠2=130°+50°=180°.
∴AB∥CD,EF∥CD.
∴AB∥EF.
6.解:∵BE平分∠ABD,DE平分∠BDC,
∴∠ABD=2∠2,∠BDC=2∠1.
∴∠ABD+∠BDC=2∠2+2∠1
=2(∠2+∠1)=2×90°=180°.
∴AB∥CD(同旁内角互补,两直线平行).
7.解:∵AB⊥BC,
∴∠ABC=90°,
即∠3+∠4=90°.
∴∠4=90°-∠3.
又∵∠1+∠2=90°,
∴∠1=90°-∠2.
又∵∠2=∠3,
∴∠4=∠1.∴BE∥DF.
解:∵DE平分∠ADC,BF平分∠ABC,
又∵∠ADC=∠ABC,
∵∠1=∠2,
∴∠CDE=∠1.
∴AB∥CD.
5.3 平行线的性质
第 1课时 平行线的性质
1. C 2. D 3. B
4.107° 5.70° 6.40° 7.42° 8.30°
9.解:(1)∵AB∥CD,
∴∠ABD+∠BDC=180°.
∵∠ABD和∠BDC的平分线交于点E,
∴∠ABD=2∠1,∠BDC=2∠2.
∴2∠1+2∠2=180°.
∴∠1+∠2=90°.
(2)∵AB∥CD,
∴∠3=∠ABF=50°.
∵BE是∠ABD的平分线,
10.解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等).
∵∠1=∠2(已知),
∴∠1=∠3(等量代换),
∴DG∥BA(内错角相等,两直线平行).
∴∠AGD+∠CAB=180°(两直线平行,同旁内角互补).
∵∠CAB=70°(已知),
∴∠AGD=110°(等式性质).
第2 课时平行线的判定与性质的综合运用
1. A 2. D 3.140°
4.解:BD∥CE.理由如下:
∵∠A=∠F.∴AC∥DF.
从而∠D=∠ABD.
∵∠C=∠D,
∴∠C=∠ABD,则BD∥CE.
5.解:∵∠1=∠2,
∴AD∥BE.
∴∠D=∠DBE.
∵∠3=∠D,
∴∠3=∠DBE,则 BD∥CE.
6.解:∵AB∥CD,
∴∠EAB=∠ECD.
∵∠1=∠2,
∴∠EAM=∠ECN.
∴AM∥CN.
7.解:(1)AD∥BC.理由如下:
∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF.∴AD∥BC.
(2)AB∥EF.理由如下:
∵BE平分∠ABC,∴∠ABC=2∠ABE.
又∠ABC=2∠E,∴∠ABE=∠E.
∴AB∥EF.
(3)∵AD∥BC,∴∠BAD+∠ABC=180°.
∵BE平分∠ABC,AF平分∠BAD,
∴∠ABE+∠BAF=90°.
由(2)得AB∥EF,
∴∠ABE=∠E,∠BAF=∠F.
∴∠E+∠F=90°.
第3课时命题、定理、证明
1. C 2. B 3. C
4.假
5.如果两条直线都和第三条直线平行,那么这两条直线也互相平行
6.90
7.①②③ 8.①②④
9.解:BF⊥AC.理由如下:
∵∠AGF=∠ABC,
∴BC∥GF(同位角相等,两直线平行).
∴∠1=∠3.
又∵∠1+∠2=180°,
∴∠2+∠3=180°.
∴BF∥DE.
∵DE⊥AC,
∴BF⊥AC.
10.(1)证明:∵MN∥PQ,∴∠DCF=∠ABC.
∵∠PDF+∠CDF=180°,∠F+∠DCF+∠CDF=180°,
∴∠PDF=∠F+∠DCF =∠F+∠ABC.
(2)解:
理由如下:
作 EG∥PQ,如图所示.
则EG∥MN∥PQ,
∴ ∠DCF = ∠ABC,∠DEG=∠PDE,∠BEG=∠MBE.
∴∠BED=∠DEG+∠BEG=∠PDE+∠MBE.
∵DE平分∠ADP,BE平分∠ABC,
又∠FDC=∠ADP,
又∠FDC+∠DCF=180°-∠F,
5.4 平移
1. D 2. D 3. B 4. C 5.平移方向平移距离
6. CD AB AC 7. BB ,CC ,DD 8.99.6 cm
10.解:将小船的各点沿箭头方向平移8格,得到对应点,顺次连接成新图即可.
所作图形如下:
第五章复习题
1. A 2. C 3. C 4. D
5.对顶角相等
CE BD 同位角相等,两直线平行
两直线平行,同位角相等
等量代换
内错角相等,两直线平行
6.解:30-2×2=26米,
26×26=676 平方米.
7.(1)证明:∵AE⊥BC,FG⊥BC,
∴AE∥FG.
∴∠1=∠CFG.
又∠1=∠2,
∴∠CFG=∠2.
∴AB∥CD.
(2)解:∵AB∥CD.
∴∠D+∠ABD=180°.
∴∠D+∠3+∠CBD=180°.
又∠D=∠3+50°,∠CBD=80°,
∴∠3=25°.
∵AB∥CD,
∴∠C=∠3=25°.
