第七章 平面直角坐标系课时强化训练(含答案)
文档属性
| 名称 | 第七章 平面直角坐标系课时强化训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 00:00:00 | ||
图片预览


文档简介
第七章 平面直角坐标系课时强化训练
7.1 平面直角坐标系
第 1课时有序数对
1.如图,一方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么 B 的位置是( )
A.(4,5) B.(5,4) C.(4,2) D.(4,3)
2.课间操时,小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成 ( )
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
3.下列数据不能确定物体位置的是 ( )
A.5 楼 6号 B.北偏东 30°
C.大学路 19 号 D.东经118°,北纬36°
4.如图,雷达探测器测得六个目标A,B,C,D,E,F出现,按照规定的目标表示方法,目标 C,F 的位置表示为C(6,120°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )
A. A(5,30°) B. B(2,90°)
C. D(4,240°) D. E(3,60°)
5.将一组数 按下面的方法进行排列:
…
若 的位置记为(1,4), 的位置记为(2,3),则这组数中最大的有理数的位置记为 ( )
A.(5,2) B.(5,3)
C.(6,2) D.(6,5)
6.剧院里5排2号可以用(5,2)表示,则(9,6)表示 .
中小学教育资源及组卷应用平台
7.在全国人民代表大会上,甲人大代表的档案袋上写着 11排8号,则工作人员可简记为(11,8),若乙人大代表的档案袋上写着15排1号,工作人员可简记为 ;若工作人员告诉丙人大代表的座位是(7,22),则丙人大代表就应当去 位置就座.
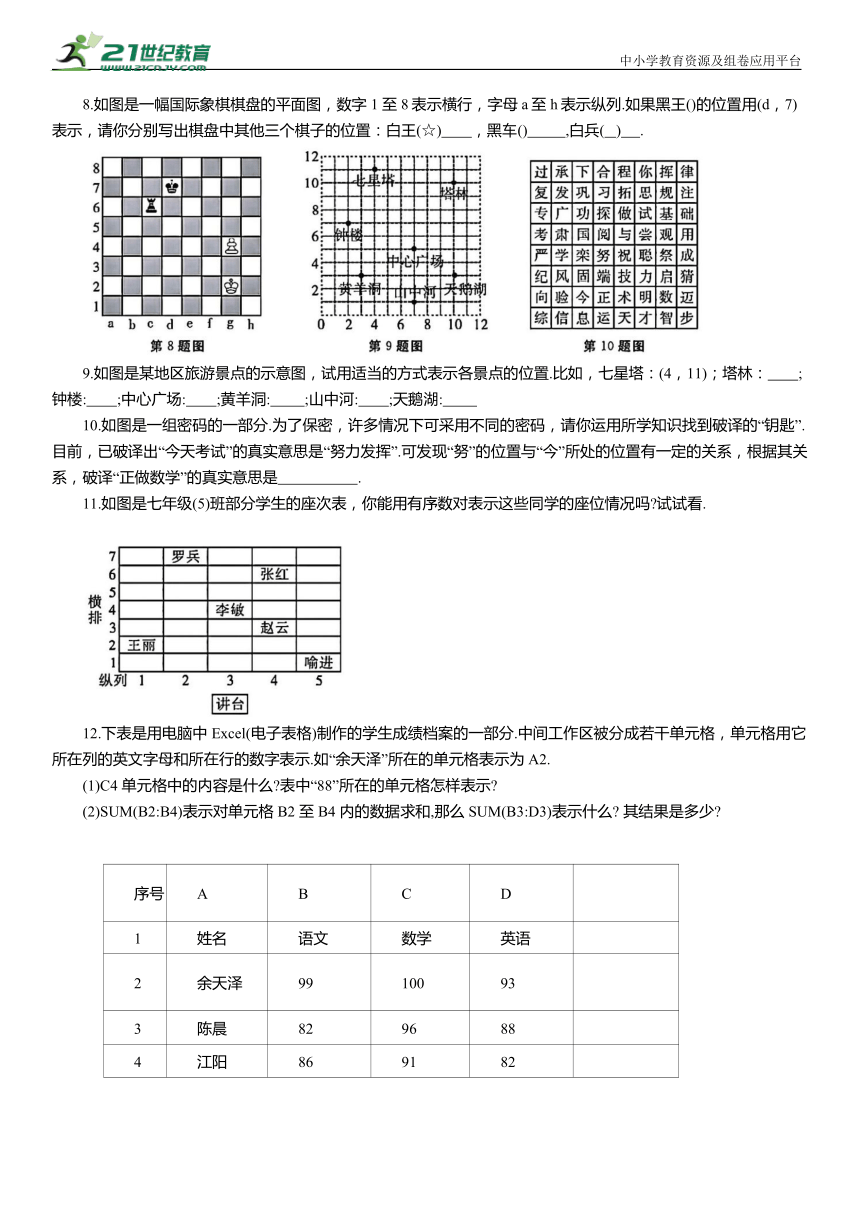
8.如图是一幅国际象棋棋盘的平面图,数字1 至 8表示横行,字母a至 h表示纵列.如果黑王()的位置用(d,7)表示,请你分别写出棋盘中其他三个棋子的位置:白王(☆) ,黑车() ,白兵( ) .
9.如图是某地区旅游景点的示意图,试用适当的方式表示各景点的位置.比如,七星塔:(4,11);塔林: ;钟楼: ;中心广场: ;黄羊洞: ;山中河: ;天鹅湖:
10.如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.可发现“努”的位置与“今”所处的位置有一定的关系,根据其关系,破译“正做数学”的真实意思是 .
11.如图是七年级(5)班部分学生的座次表,你能用有序数对表示这些同学的座位情况吗 试试看.
12.下表是用电脑中 Excel(电子表格)制作的学生成绩档案的一部分.中间工作区被分成若干单元格,单元格用它所在列的英文字母和所在行的数字表示.如“余天泽”所在的单元格表示为 A2.
(1)C4 单元格中的内容是什么 表中“88”所在的单元格怎样表示
(2)SUM(B2:B4)表示对单元格 B2 至 B4 内的数据求和,那么 SUM(B3:D3)表示什么 其结果是多少
序号 A B C D
1 姓名 语文 数学 英语
2 余天泽 99 100 93
3 陈晨 82 96 88
4 江阳 86 91 82
第 2 课时 平面直角坐标系(1)——点的坐标
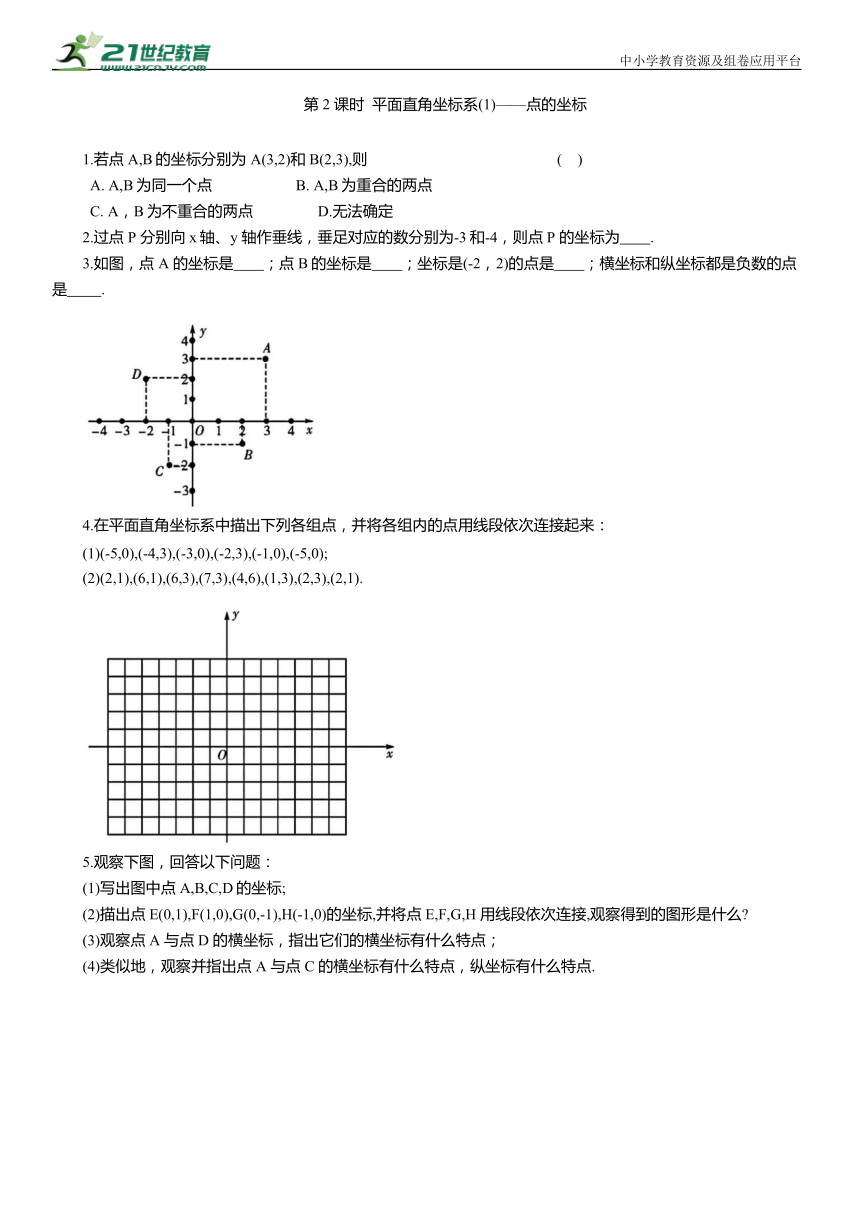
1.若点A,B的坐标分别为A(3,2)和B(2,3),则 ( )
A. A,B为同一个点 B. A,B为重合的两点
C. A,B为不重合的两点 D.无法确定
2.过点 P 分别向x轴、y 轴作垂线,垂足对应的数分别为-3和-4,则点 P 的坐标为 .
3.如图,点 A 的坐标是 ;点B的坐标是 ;坐标是(-2,2)的点是 ;横坐标和纵坐标都是负数的点是 .
4.在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来:
(1)(-5,0),(-4,3),(-3,0),(-2,3),(-1,0),(-5,0);
(2)(2,1),(6,1),(6,3),(7,3),(4,6),(1,3),(2,3),(2,1).
5.观察下图,回答以下问题:
(1)写出图中点 A,B,C,D的坐标;
(2)描出点E(0,1),F(1,0),G(0,-1),H(-1,0)的坐标,并将点 E,F,G,H 用线段依次连接,观察得到的图形是什么
(3)观察点 A 与点D 的横坐标,指出它们的横坐标有什么特点;
(4)类似地,观察并指出点 A 与点C 的横坐标有什么特点,纵坐标有什么特点.
第3课时 平面直角坐标系(2)——点的坐标特征
1.如图,小手盖住的点的坐标可能为 ( )
A.(4,3) B.(-5,2) C.(-2,-4) D.(2,-5)
2.若点 A(-2,n)在x轴上,则点 B(n-2,n+1)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系中,下列各点中到x轴的距离最近的点是 ( )
A.(2,5) B.(-4,1) C.(3,-4) D.(6,2)
4.平面直角坐标系中有一点A,且A 点到x 轴的距离为3,A 点到y 轴的距离恰为到x 轴距离的3倍.若 A 点在第二象限,则 A点坐标为 ( )
A.(-9,3) B.(-3,1) C.(-3,9) D.(-1,3)
5.在平面直角坐标系xOy中,若A点坐标为(-3,3),B点坐标为(2,0),则三角形 ABO的面积为( )
A.15 B.7.5 C.6 D.3
6.在平面直角坐标系中,点(4,—4)在第 象限.
7.点P(-3,5)到x轴的距离是 ,到y轴的距离是 .
8.若点(-2,m-1)在第二象限,则点(m,-2)在第 象限.
9.已知点 P(2m+4,m-1),试分别根据下列条件,求出点 P 的坐标.
(1)点 P 在 y 轴上;
(2)点 P 的纵坐标比横坐标大3;
(3)点 P 到x轴的距离为2,且在第四象限.
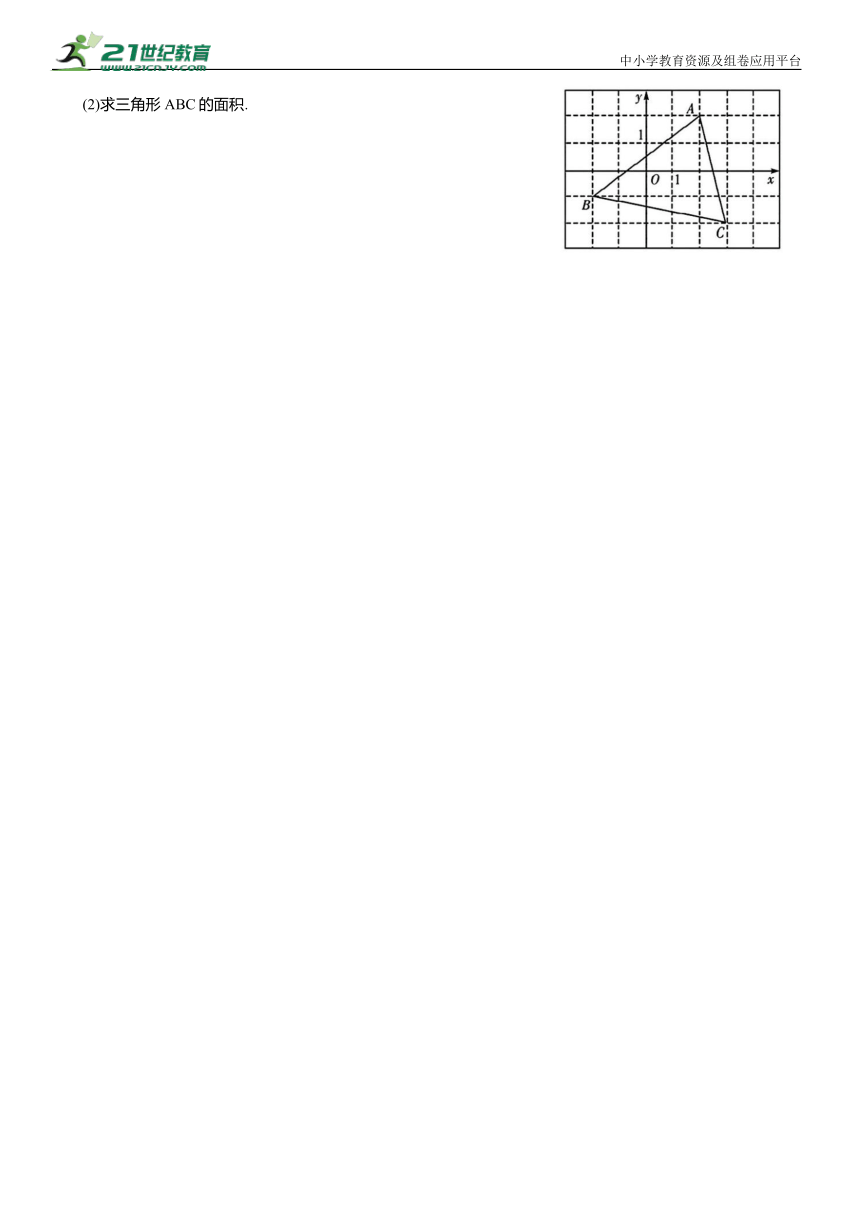
10.如图,平面直角坐标系中有三角形 ABC.
(1)写出三角形 ABC的三个顶点坐标;
(2)求三角形 ABC的面积.
7.2 坐标方法的简单应用
第1课时 用坐标表示地理位置
1.从车站向东走400米,再向北走 500米到小红家;从车站向北走 500米,再向西走 200米到小强家.则 ( )
A.小强家在小红家的正东 B.小强家在小红家的正西
C.小强家在小红家的正南 D.小强家在小红家的正北
2.在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点A(3,3),B(5,1),则“宝藏”所在地点 C 的坐标为 ( )
A.(6,4) B.(3,3) C.(6,5) D.(3,4)
3.如图为小杰使用手机内的通讯软件跟小智对话的记录,根据图中两人的对话,若下列有一种走法能从邮局出发走到小杰家,则此走法为 ( )
A.向北直走 700米,再向西直走 100米 B.向北直走 100米,再向东直走 700米
C.向北直走 300米,再向西直走 400 米 D.向北直走 400米,再向东直走 300 米
4.在平面直角坐标系中有A,B两点,若以 B点为原点建立平面直角坐标系,则A点的坐标为(2,3),若以A点为原点建立平面直角坐标系(两直角坐标系x轴,y轴方向一致),则 B点的坐标为 ( )
A.(-2,-3) B.(-2,3) C.(2,-3) D.(2,3)
5.在平面直角坐标系中,小明做走棋游戏,其走法是:棋子从原点起,第1步向右走1个单位长度,第2步向右走2个单位长度,第3步向上走 1个单位长度,第4步向右走1个单位长度,….依此类推,第n步是:当n能被3整除时,则向上走1个单位长度;当n被3除,余数是1时,则向右走1个单位长度;当n被3除,余数为2时,则向右走 2个单位长度.当他走完第100步时,棋子所处位置的坐标是 ( )
A.(66,34) B.(67,33)
C.(100,33) D.(99,34)
6.如图是新疆主要城市的大致分布图,方格中的每个小正方形边长为1个单位长度,如果喀什市所在地用坐标表示为(--4,-3),哈密市所在地用坐标表示为(3,-1),那么阿勒泰市所在地用坐标表示为 ,阿克苏市所在地用坐标表示为
7.图中小玲家在商场的 方向上,距离约 米.
8.已知点A(a,5),B(2,2-b),C(4,2),且AB平行于x轴,AC平行于y轴,则a+b= .
9.点A(0,-3),点B(0,2),点C在x轴上,若三角形ABC的面积为15,则点C的坐标是 .
10.将正整数按如图所示的规律排列下去,若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示正整数9,则(7,2)表示的正整数是 .
11.五子棋深受广大棋友的喜爱.规则是:10×10的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上首先连成五颗者为胜.如图是小张和小王的对弈图(小张执黑子先行,小王执白子后走).观察棋盘思考:若A 点的位置记作(8,4),小张必须在哪个位置上落子才不会让小王在短时间内获胜 为什么
12.某次海战中敌我双方舰艇对峙示意图(图中1 cm代表20海里)如下,对我方潜艇O来说:
(1)北偏东40°的方向上有哪些目标 要想确定敌舰B的位置,还需要什么数据
(2)距离我方潜艇20海里的敌舰有哪几艘
(3)要确定每艘敌舰的位置,各需要几个数据
第2课时 用坐标表示平移
1.将点 A(2,1)向左平移2个单位长度得到点 A',则点 A'的坐标是 ( )
A.(2,3) B.(2,-1) C.(4,1) D.(0,1)
2.在平面直角坐标系中,点A(1,2)平移后的坐标是A'(-3,3),按照同样的规律平移其他点,则符合这种要求的变换是 ( )
A.(3,2)→(4,—2) B.(-1,0)→(-5,-4)
D.(1.5,5)→(-3.2,6)
3.如图,把图(1)中的圆A 经过平移得到圆O[如图(2)],如果图(1)中圆A上一点P 的坐标为(m,n),那么平移后点 P 在图(2)中的对应点 P'的坐标为 ( )
A.(m+2,n+1) B.(m-2,n-1) C.(m—2,n+1) D.(m+2,n-1)
4.将△ABC的三个顶点的横坐标都加上一6,纵坐标都减去5,则所得图形与原图形的关系是 ( )
A.将原图形向x轴的正方向平移了6个单位长度,向y轴的正方向平移了5个单位长度
B.将原图形向x轴的负方向平移了6个单位长度,向y轴的正方向平移了5个单位长度
C.将原图形向x轴的负方向平移了 6个单位长度,向y轴的负方向平移了5个单位长度
D.将原图形向x轴的正方向平移了6个单位长度,向y轴的负方向平移了5个单位长度
5.如图,将四边形 ABCD 先向左平移3个单位长度,再向上平移2个单位长度,那么点 A 对应的点A'的坐标是 ( )
A.(6,1) B.(0,1) C.(0,-3) D.(6,-3)
6.在平面直角坐标系中,点M(1,一2)可由点N(1,0)经过向 平移 个单位长度得到.
7.在平面直角坐标系中,已知点O(0,0),A(1,3),将线段OA 向右平移3个单位长度,得到线段O A ,则点 O 的坐标是 ,A 的坐标是 .
8.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B 的坐标分别为(--1,0),(0, ).现将该三角板向右平移使点A 与点O重合,点O,B的对应点分别为点C,B',则线段
如图,A,B的坐标分别为(1,0),(0,2),若将线段AB平移至 的坐标分别为(2,a),(b,3),则
10.在平面直角坐标系中,已知A(-4,1),B(0,2),将线段AB 平移,使 A 与坐标原点O重合,则 B 平移后的坐标是 .
11.已知三角形ABC各顶点的坐标为 ,将三角形ABC先向右平移4个单位长度,再向上平移3个单位长度得到三角形
(1)在直角坐标系中画出三角形.
(2)求出三角形 的面积.
12.如图,一只甲虫在( 的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B,C,D处的其他甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B 记为: 从C到D 记为: 其中第一个数表示左右方向,第二个数表示上下方向.
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)假如这只甲虫从A 处去甲虫P 处的行走路线依次为( ,请在图中标出 P 的位置.
第七章复习题
1.在平面直角坐标系中,点(1,2)位于第 象限.
2.将点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个长度单位后得到点 A'的坐标为 .
3.如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则将此“QQ”笑脸向右平移5个单位长度后,右眼 B的坐标是 .
4.在平面直角坐标系中,线段 AB的两个端点的坐标分别为A(-2,1),B(1,3),将线段 AB 经过平移后得到线段A'B',若点A的对应点为A'(3,2),则点 B的对应点B'的坐标是 .
5.如果m是任意实数,则点P(m-4,m+1)一定不在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知点M到x轴的距离为1,到y轴的距离为2,则M点的坐标为 ( )
A.(1,2) B.(-1,-2)
C.(1,-2) D.(2,1),(2,—1),(—2,1),(—2,—1)
7.已知在第二象限内的点 P(x,y)满足| ,则点 P 的坐标是 .
8.如图,正方形 ABCD的边长为4,点A的坐标为(一1,1),AB平行于x 轴,则点 C 的坐标为 .
9.在平面直角坐标系中,若点 M(1,3)与点 N(x,3)之间的距离是5,则x的值是 .
10.如图,在边长为1的正方形网格中,A(2,4),B(4,1),C(-3,4).
(1)平移线段AB到线段CD,使点A 与点C重合,则点 D 的坐标为 ;
(2)求线段AB平移至线段CD 处所扫过的面积;
(3)平移线段AB,使其两端点都在坐标轴上,求点 A的对应点A 的坐标.
第七章 平面直角坐标系
7.1平面直角坐标系
第 1 课时 有序数对
1. A 2. D 3. B 4. D
5.C 解析:将所有数写成开方形式,易发现规律:从第2个数开始,每个数的被开方都比上个数的被开方数大3.位置排列规律为每一行有5个数,每个数的位置由一对有序数对表示.其中第一个数代表行数,第二个数代表列数.所给的数中最大的有理数为 即9.由于 所以 位于第6行,第2列,记为(6,2).故选 C.
6.9排6号
7.(15,1) 7 排22号
8.(g,2) (c,6) (g,4)
9.(10,10) (2,7) (7,5) (3,3) (7,1) (10,3)
10.祝你成功 解析:由“今天考试”的真正意思是“努力发挥”可得出破译钥匙:该字上方2个格,再向右边1格的位置是真实的字意,由此规律可得出答案.
11.解:如果规定“列数在前,排数在后”,那么表示这些同学座位的有序数对为:王丽(1,2),罗兵(2.7),李敏(3,4),张红(4,6),赵云(4,3),喻进(5,1).
12.(1)91;D3.
(2)对单元格 B3 至 D3内的数据求和;266.
第 2 课时 平面直角坐标系(1)———点的坐标1. C 2.(-3.-4) 3.(3,3) (2,-1) 点 D 点 C4.略
5.(1)A(4,2),B(-3,-2),C(-4,3),D(4,-1).
(2)图略,正方形.
(3)点 A,D的横坐标相同.
(4)点A,C的横坐标互为相反数,纵坐标不同.
第3课时 平面直角坐标系(2)———点的坐标特征1. C 2. B 3. B 4. A 5. D 6.四 7.5 3 8.四9.解:(1)∵点 P(2m+4,m-1)在 y轴上,
∴2m+4=0,解得m=-2.
∴m-1=-2-1=-3.
∴点 P 的坐标为(0,-3).
(2)∵点P 的纵坐标比横坐标大3,
∴(m-1)-(2m+4)=3,解得m=-8.
∴m-1=-8-1=-9,2m+4=2×(-8)+4=-12.
∴点 P 的坐标为(-12,-9).
(3)∵点 P到x轴的距离为2,∴|m-1|=2.
∵点 P 在第四象限,∴m-1<0.
∴m-1=-2,解得m=-1.
此时,2m+4=2×(-1)+4=2,m-1=-1-1=-2,∴点 P(2,-2).
10.解:(1)A(2,2),B(-2,-1),C(3,-2).
(2)三角形 ABC 的面积为
7.2 坐标方法的简单应用
第1 课时 用坐标表示地理位置
1. B 2. A
3. A 解析:根据题意先画图(如图),可得出AE=CE=400米,AB=CD=300米,再得出 DE=100米,故可得出从邮局出发走到小杰家的一种走法为:向北直走 AB+AE=700米,再向西直走 DE=100米.
4.A 解析:根据题意作出图形即可解决.
5. C
6.(0,2) (-2,-2)
7.南偏东 60° 800
8.1
9.(6,0)或(-6,0) 10.23
11.必须在(1,7)或(5,3)处落子,才不会让小王在短时间内获胜.
12.(1)敌舰 B和小岛,敌舰 B距我方潜艇的距离.
(2)敌舰 A和敌舰C.
(3)距离和方位角.
第 2 课时 用坐标表示平移
1. D 2. C 3. D 4. C 5. B
6.下 2 7.(3,0) (4,3) 8.1 9.2
10.(4,1)
11.解:(1)如图所示,三角形A'B'C'即为所求.
(2)三角形 A'B'C'的面积为
12.(1)+3 +4 B --1 (2)10
(3)
第七章复习题
1.一 2.(2,—2) 3.(5,3) 4.(6,4)
5. D 6. D 7.(-5,2) 8.(3,5) 9.6或-4
10.解:(1)∵平移线段 AB 到线段CD,使点 A 与点 C 重合,A(2,4),C(-3,4),
∴坐标变化规律是:横坐标减去5,纵坐标不变.
∵B(4,1),∴点 D 的坐标为(-1,1).
(2)由平移的性质可得线段 AB 平移至线段 CD处所扫过的图形是平行四边形 ABDC,其面积为5×3=15.
(3)分两种情况:
①如果平移后 A 的对应点在 y 轴上,B 的对应点在x轴上,
那么坐标变化规律是:横坐标减去 2,纵坐标减去1.
∵A(2,4),∴点 A 的坐标为(0,3).
②如果平移后A的对应点在x轴上,B的对应点在y轴上,
那么坐标变化规律是:横坐标减去 4.纵坐标减去4.
∵A(2,4),∴点 A 的坐标为(-2,0).
故点 A的对应点A 的坐标为(0,3)或(-2,0).
7.1 平面直角坐标系
第 1课时有序数对
1.如图,一方队正沿箭头所指的方向前进,A的位置为三列四行,表示为(3,4),那么 B 的位置是( )
A.(4,5) B.(5,4) C.(4,2) D.(4,3)
2.课间操时,小华、小军、小刚的位置如图所示,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成 ( )
A.(5,4) B.(4,5) C.(3,4) D.(4,3)
3.下列数据不能确定物体位置的是 ( )
A.5 楼 6号 B.北偏东 30°
C.大学路 19 号 D.东经118°,北纬36°
4.如图,雷达探测器测得六个目标A,B,C,D,E,F出现,按照规定的目标表示方法,目标 C,F 的位置表示为C(6,120°),F(5,210°),按照此方法在表示目标A,B,D,E的位置时,其中表示不正确的是( )
A. A(5,30°) B. B(2,90°)
C. D(4,240°) D. E(3,60°)
5.将一组数 按下面的方法进行排列:
…
若 的位置记为(1,4), 的位置记为(2,3),则这组数中最大的有理数的位置记为 ( )
A.(5,2) B.(5,3)
C.(6,2) D.(6,5)
6.剧院里5排2号可以用(5,2)表示,则(9,6)表示 .
中小学教育资源及组卷应用平台
7.在全国人民代表大会上,甲人大代表的档案袋上写着 11排8号,则工作人员可简记为(11,8),若乙人大代表的档案袋上写着15排1号,工作人员可简记为 ;若工作人员告诉丙人大代表的座位是(7,22),则丙人大代表就应当去 位置就座.
8.如图是一幅国际象棋棋盘的平面图,数字1 至 8表示横行,字母a至 h表示纵列.如果黑王()的位置用(d,7)表示,请你分别写出棋盘中其他三个棋子的位置:白王(☆) ,黑车() ,白兵( ) .
9.如图是某地区旅游景点的示意图,试用适当的方式表示各景点的位置.比如,七星塔:(4,11);塔林: ;钟楼: ;中心广场: ;黄羊洞: ;山中河: ;天鹅湖:
10.如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”.目前,已破译出“今天考试”的真实意思是“努力发挥”.可发现“努”的位置与“今”所处的位置有一定的关系,根据其关系,破译“正做数学”的真实意思是 .
11.如图是七年级(5)班部分学生的座次表,你能用有序数对表示这些同学的座位情况吗 试试看.
12.下表是用电脑中 Excel(电子表格)制作的学生成绩档案的一部分.中间工作区被分成若干单元格,单元格用它所在列的英文字母和所在行的数字表示.如“余天泽”所在的单元格表示为 A2.
(1)C4 单元格中的内容是什么 表中“88”所在的单元格怎样表示
(2)SUM(B2:B4)表示对单元格 B2 至 B4 内的数据求和,那么 SUM(B3:D3)表示什么 其结果是多少
序号 A B C D
1 姓名 语文 数学 英语
2 余天泽 99 100 93
3 陈晨 82 96 88
4 江阳 86 91 82
第 2 课时 平面直角坐标系(1)——点的坐标
1.若点A,B的坐标分别为A(3,2)和B(2,3),则 ( )
A. A,B为同一个点 B. A,B为重合的两点
C. A,B为不重合的两点 D.无法确定
2.过点 P 分别向x轴、y 轴作垂线,垂足对应的数分别为-3和-4,则点 P 的坐标为 .
3.如图,点 A 的坐标是 ;点B的坐标是 ;坐标是(-2,2)的点是 ;横坐标和纵坐标都是负数的点是 .
4.在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来:
(1)(-5,0),(-4,3),(-3,0),(-2,3),(-1,0),(-5,0);
(2)(2,1),(6,1),(6,3),(7,3),(4,6),(1,3),(2,3),(2,1).
5.观察下图,回答以下问题:
(1)写出图中点 A,B,C,D的坐标;
(2)描出点E(0,1),F(1,0),G(0,-1),H(-1,0)的坐标,并将点 E,F,G,H 用线段依次连接,观察得到的图形是什么
(3)观察点 A 与点D 的横坐标,指出它们的横坐标有什么特点;
(4)类似地,观察并指出点 A 与点C 的横坐标有什么特点,纵坐标有什么特点.
第3课时 平面直角坐标系(2)——点的坐标特征
1.如图,小手盖住的点的坐标可能为 ( )
A.(4,3) B.(-5,2) C.(-2,-4) D.(2,-5)
2.若点 A(-2,n)在x轴上,则点 B(n-2,n+1)在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.在平面直角坐标系中,下列各点中到x轴的距离最近的点是 ( )
A.(2,5) B.(-4,1) C.(3,-4) D.(6,2)
4.平面直角坐标系中有一点A,且A 点到x 轴的距离为3,A 点到y 轴的距离恰为到x 轴距离的3倍.若 A 点在第二象限,则 A点坐标为 ( )
A.(-9,3) B.(-3,1) C.(-3,9) D.(-1,3)
5.在平面直角坐标系xOy中,若A点坐标为(-3,3),B点坐标为(2,0),则三角形 ABO的面积为( )
A.15 B.7.5 C.6 D.3
6.在平面直角坐标系中,点(4,—4)在第 象限.
7.点P(-3,5)到x轴的距离是 ,到y轴的距离是 .
8.若点(-2,m-1)在第二象限,则点(m,-2)在第 象限.
9.已知点 P(2m+4,m-1),试分别根据下列条件,求出点 P 的坐标.
(1)点 P 在 y 轴上;
(2)点 P 的纵坐标比横坐标大3;
(3)点 P 到x轴的距离为2,且在第四象限.
10.如图,平面直角坐标系中有三角形 ABC.
(1)写出三角形 ABC的三个顶点坐标;
(2)求三角形 ABC的面积.
7.2 坐标方法的简单应用
第1课时 用坐标表示地理位置
1.从车站向东走400米,再向北走 500米到小红家;从车站向北走 500米,再向西走 200米到小强家.则 ( )
A.小强家在小红家的正东 B.小强家在小红家的正西
C.小强家在小红家的正南 D.小强家在小红家的正北
2.在一次“寻宝”游戏中,“寻宝”人找到了如图所示标志点A(3,3),B(5,1),则“宝藏”所在地点 C 的坐标为 ( )
A.(6,4) B.(3,3) C.(6,5) D.(3,4)
3.如图为小杰使用手机内的通讯软件跟小智对话的记录,根据图中两人的对话,若下列有一种走法能从邮局出发走到小杰家,则此走法为 ( )
A.向北直走 700米,再向西直走 100米 B.向北直走 100米,再向东直走 700米
C.向北直走 300米,再向西直走 400 米 D.向北直走 400米,再向东直走 300 米
4.在平面直角坐标系中有A,B两点,若以 B点为原点建立平面直角坐标系,则A点的坐标为(2,3),若以A点为原点建立平面直角坐标系(两直角坐标系x轴,y轴方向一致),则 B点的坐标为 ( )
A.(-2,-3) B.(-2,3) C.(2,-3) D.(2,3)
5.在平面直角坐标系中,小明做走棋游戏,其走法是:棋子从原点起,第1步向右走1个单位长度,第2步向右走2个单位长度,第3步向上走 1个单位长度,第4步向右走1个单位长度,….依此类推,第n步是:当n能被3整除时,则向上走1个单位长度;当n被3除,余数是1时,则向右走1个单位长度;当n被3除,余数为2时,则向右走 2个单位长度.当他走完第100步时,棋子所处位置的坐标是 ( )
A.(66,34) B.(67,33)
C.(100,33) D.(99,34)
6.如图是新疆主要城市的大致分布图,方格中的每个小正方形边长为1个单位长度,如果喀什市所在地用坐标表示为(--4,-3),哈密市所在地用坐标表示为(3,-1),那么阿勒泰市所在地用坐标表示为 ,阿克苏市所在地用坐标表示为
7.图中小玲家在商场的 方向上,距离约 米.
8.已知点A(a,5),B(2,2-b),C(4,2),且AB平行于x轴,AC平行于y轴,则a+b= .
9.点A(0,-3),点B(0,2),点C在x轴上,若三角形ABC的面积为15,则点C的坐标是 .
10.将正整数按如图所示的规律排列下去,若用有序实数对(n,m)表示第n排,从左到右第m个数,如(4,3)表示正整数9,则(7,2)表示的正整数是 .
11.五子棋深受广大棋友的喜爱.规则是:10×10的正方形棋盘中,由黑方先行,轮流弈子,在任一方向上首先连成五颗者为胜.如图是小张和小王的对弈图(小张执黑子先行,小王执白子后走).观察棋盘思考:若A 点的位置记作(8,4),小张必须在哪个位置上落子才不会让小王在短时间内获胜 为什么
12.某次海战中敌我双方舰艇对峙示意图(图中1 cm代表20海里)如下,对我方潜艇O来说:
(1)北偏东40°的方向上有哪些目标 要想确定敌舰B的位置,还需要什么数据
(2)距离我方潜艇20海里的敌舰有哪几艘
(3)要确定每艘敌舰的位置,各需要几个数据
第2课时 用坐标表示平移
1.将点 A(2,1)向左平移2个单位长度得到点 A',则点 A'的坐标是 ( )
A.(2,3) B.(2,-1) C.(4,1) D.(0,1)
2.在平面直角坐标系中,点A(1,2)平移后的坐标是A'(-3,3),按照同样的规律平移其他点,则符合这种要求的变换是 ( )
A.(3,2)→(4,—2) B.(-1,0)→(-5,-4)
D.(1.5,5)→(-3.2,6)
3.如图,把图(1)中的圆A 经过平移得到圆O[如图(2)],如果图(1)中圆A上一点P 的坐标为(m,n),那么平移后点 P 在图(2)中的对应点 P'的坐标为 ( )
A.(m+2,n+1) B.(m-2,n-1) C.(m—2,n+1) D.(m+2,n-1)
4.将△ABC的三个顶点的横坐标都加上一6,纵坐标都减去5,则所得图形与原图形的关系是 ( )
A.将原图形向x轴的正方向平移了6个单位长度,向y轴的正方向平移了5个单位长度
B.将原图形向x轴的负方向平移了6个单位长度,向y轴的正方向平移了5个单位长度
C.将原图形向x轴的负方向平移了 6个单位长度,向y轴的负方向平移了5个单位长度
D.将原图形向x轴的正方向平移了6个单位长度,向y轴的负方向平移了5个单位长度
5.如图,将四边形 ABCD 先向左平移3个单位长度,再向上平移2个单位长度,那么点 A 对应的点A'的坐标是 ( )
A.(6,1) B.(0,1) C.(0,-3) D.(6,-3)
6.在平面直角坐标系中,点M(1,一2)可由点N(1,0)经过向 平移 个单位长度得到.
7.在平面直角坐标系中,已知点O(0,0),A(1,3),将线段OA 向右平移3个单位长度,得到线段O A ,则点 O 的坐标是 ,A 的坐标是 .
8.如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B 的坐标分别为(--1,0),(0, ).现将该三角板向右平移使点A 与点O重合,点O,B的对应点分别为点C,B',则线段
如图,A,B的坐标分别为(1,0),(0,2),若将线段AB平移至 的坐标分别为(2,a),(b,3),则
10.在平面直角坐标系中,已知A(-4,1),B(0,2),将线段AB 平移,使 A 与坐标原点O重合,则 B 平移后的坐标是 .
11.已知三角形ABC各顶点的坐标为 ,将三角形ABC先向右平移4个单位长度,再向上平移3个单位长度得到三角形
(1)在直角坐标系中画出三角形.
(2)求出三角形 的面积.
12.如图,一只甲虫在( 的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B,C,D处的其他甲虫,规定:向上向右走为正,向下向左走为负.如果从A到B 记为: 从C到D 记为: 其中第一个数表示左右方向,第二个数表示上下方向.
(2)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程;
(3)假如这只甲虫从A 处去甲虫P 处的行走路线依次为( ,请在图中标出 P 的位置.
第七章复习题
1.在平面直角坐标系中,点(1,2)位于第 象限.
2.将点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个长度单位后得到点 A'的坐标为 .
3.如图,把“QQ”笑脸放在直角坐标系中,已知左眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则将此“QQ”笑脸向右平移5个单位长度后,右眼 B的坐标是 .
4.在平面直角坐标系中,线段 AB的两个端点的坐标分别为A(-2,1),B(1,3),将线段 AB 经过平移后得到线段A'B',若点A的对应点为A'(3,2),则点 B的对应点B'的坐标是 .
5.如果m是任意实数,则点P(m-4,m+1)一定不在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知点M到x轴的距离为1,到y轴的距离为2,则M点的坐标为 ( )
A.(1,2) B.(-1,-2)
C.(1,-2) D.(2,1),(2,—1),(—2,1),(—2,—1)
7.已知在第二象限内的点 P(x,y)满足| ,则点 P 的坐标是 .
8.如图,正方形 ABCD的边长为4,点A的坐标为(一1,1),AB平行于x 轴,则点 C 的坐标为 .
9.在平面直角坐标系中,若点 M(1,3)与点 N(x,3)之间的距离是5,则x的值是 .
10.如图,在边长为1的正方形网格中,A(2,4),B(4,1),C(-3,4).
(1)平移线段AB到线段CD,使点A 与点C重合,则点 D 的坐标为 ;
(2)求线段AB平移至线段CD 处所扫过的面积;
(3)平移线段AB,使其两端点都在坐标轴上,求点 A的对应点A 的坐标.
第七章 平面直角坐标系
7.1平面直角坐标系
第 1 课时 有序数对
1. A 2. D 3. B 4. D
5.C 解析:将所有数写成开方形式,易发现规律:从第2个数开始,每个数的被开方都比上个数的被开方数大3.位置排列规律为每一行有5个数,每个数的位置由一对有序数对表示.其中第一个数代表行数,第二个数代表列数.所给的数中最大的有理数为 即9.由于 所以 位于第6行,第2列,记为(6,2).故选 C.
6.9排6号
7.(15,1) 7 排22号
8.(g,2) (c,6) (g,4)
9.(10,10) (2,7) (7,5) (3,3) (7,1) (10,3)
10.祝你成功 解析:由“今天考试”的真正意思是“努力发挥”可得出破译钥匙:该字上方2个格,再向右边1格的位置是真实的字意,由此规律可得出答案.
11.解:如果规定“列数在前,排数在后”,那么表示这些同学座位的有序数对为:王丽(1,2),罗兵(2.7),李敏(3,4),张红(4,6),赵云(4,3),喻进(5,1).
12.(1)91;D3.
(2)对单元格 B3 至 D3内的数据求和;266.
第 2 课时 平面直角坐标系(1)———点的坐标1. C 2.(-3.-4) 3.(3,3) (2,-1) 点 D 点 C4.略
5.(1)A(4,2),B(-3,-2),C(-4,3),D(4,-1).
(2)图略,正方形.
(3)点 A,D的横坐标相同.
(4)点A,C的横坐标互为相反数,纵坐标不同.
第3课时 平面直角坐标系(2)———点的坐标特征1. C 2. B 3. B 4. A 5. D 6.四 7.5 3 8.四9.解:(1)∵点 P(2m+4,m-1)在 y轴上,
∴2m+4=0,解得m=-2.
∴m-1=-2-1=-3.
∴点 P 的坐标为(0,-3).
(2)∵点P 的纵坐标比横坐标大3,
∴(m-1)-(2m+4)=3,解得m=-8.
∴m-1=-8-1=-9,2m+4=2×(-8)+4=-12.
∴点 P 的坐标为(-12,-9).
(3)∵点 P到x轴的距离为2,∴|m-1|=2.
∵点 P 在第四象限,∴m-1<0.
∴m-1=-2,解得m=-1.
此时,2m+4=2×(-1)+4=2,m-1=-1-1=-2,∴点 P(2,-2).
10.解:(1)A(2,2),B(-2,-1),C(3,-2).
(2)三角形 ABC 的面积为
7.2 坐标方法的简单应用
第1 课时 用坐标表示地理位置
1. B 2. A
3. A 解析:根据题意先画图(如图),可得出AE=CE=400米,AB=CD=300米,再得出 DE=100米,故可得出从邮局出发走到小杰家的一种走法为:向北直走 AB+AE=700米,再向西直走 DE=100米.
4.A 解析:根据题意作出图形即可解决.
5. C
6.(0,2) (-2,-2)
7.南偏东 60° 800
8.1
9.(6,0)或(-6,0) 10.23
11.必须在(1,7)或(5,3)处落子,才不会让小王在短时间内获胜.
12.(1)敌舰 B和小岛,敌舰 B距我方潜艇的距离.
(2)敌舰 A和敌舰C.
(3)距离和方位角.
第 2 课时 用坐标表示平移
1. D 2. C 3. D 4. C 5. B
6.下 2 7.(3,0) (4,3) 8.1 9.2
10.(4,1)
11.解:(1)如图所示,三角形A'B'C'即为所求.
(2)三角形 A'B'C'的面积为
12.(1)+3 +4 B --1 (2)10
(3)
第七章复习题
1.一 2.(2,—2) 3.(5,3) 4.(6,4)
5. D 6. D 7.(-5,2) 8.(3,5) 9.6或-4
10.解:(1)∵平移线段 AB 到线段CD,使点 A 与点 C 重合,A(2,4),C(-3,4),
∴坐标变化规律是:横坐标减去5,纵坐标不变.
∵B(4,1),∴点 D 的坐标为(-1,1).
(2)由平移的性质可得线段 AB 平移至线段 CD处所扫过的图形是平行四边形 ABDC,其面积为5×3=15.
(3)分两种情况:
①如果平移后 A 的对应点在 y 轴上,B 的对应点在x轴上,
那么坐标变化规律是:横坐标减去 2,纵坐标减去1.
∵A(2,4),∴点 A 的坐标为(0,3).
②如果平移后A的对应点在x轴上,B的对应点在y轴上,
那么坐标变化规律是:横坐标减去 4.纵坐标减去4.
∵A(2,4),∴点 A 的坐标为(-2,0).
故点 A的对应点A 的坐标为(0,3)或(-2,0).
