第五章相交线与平行线检测卷(含答案)
文档属性
| 名称 | 第五章相交线与平行线检测卷(含答案) | 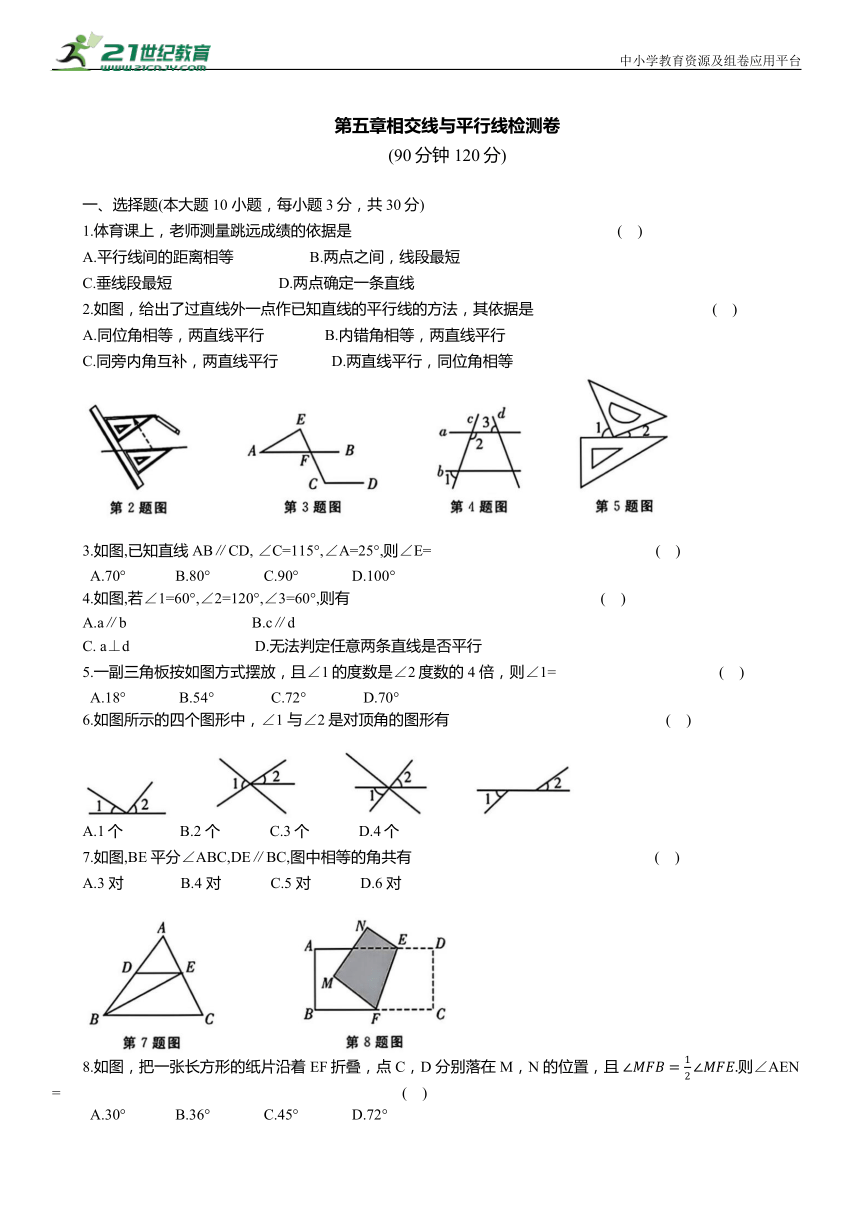 | |
| 格式 | docx | ||
| 文件大小 | 927.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 09:43:20 | ||
图片预览

文档简介
第五章相交线与平行线检测卷
(90分钟 120分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.体育课上,老师测量跳远成绩的依据是 ( )
A.平行线间的距离相等 B.两点之间,线段最短
C.垂线段最短 D.两点确定一条直线
2.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 ( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
3.如图,已知直线AB∥CD, ∠C=115°,∠A=25°,则∠E= ( )
A.70° B.80° C.90° D.100°
4.如图,若∠1=60°,∠2=120°,∠3=60°,则有 ( )
A.a∥b B.c∥d
C. a⊥d D.无法判定任意两条直线是否平行
5.一副三角板按如图方式摆放,且∠1的度数是∠2度数的4 倍,则∠1= ( )
A.18° B.54° C.72° D.70°
6.如图所示的四个图形中,∠1 与∠2是对顶角的图形有 ( )
A.1个 B.2 个 C.3个 D.4个
7.如图,BE平分∠ABC,DE∥BC,图中相等的角共有 ( )
A.3 对 B.4 对 C.5 对 D.6 对
8.如图,把一张长方形的纸片沿着 EF折叠,点 C,D 分别落在M,N 的位置,且 则∠AEN= ( )
中小学教育资源及组卷应用平台
A.30° B.36° C.45° D.72°
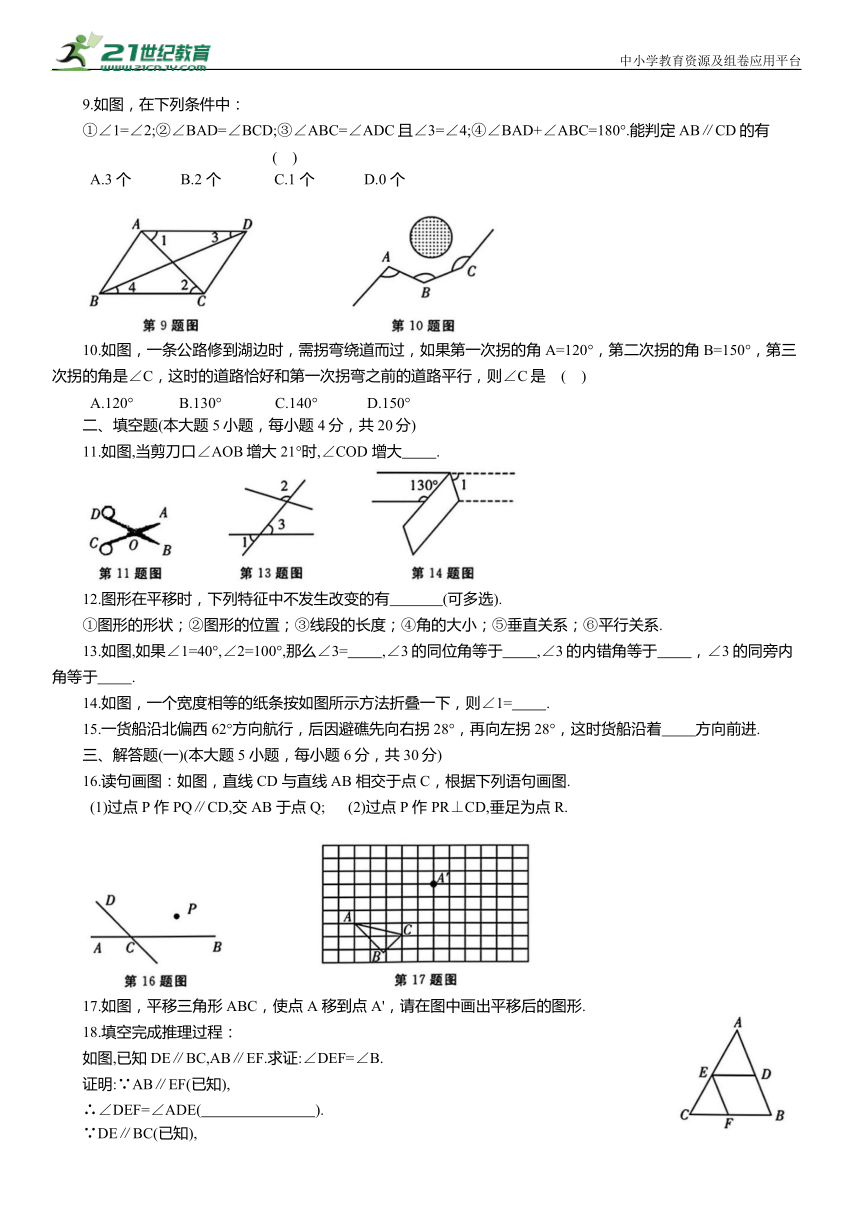
9.如图,在下列条件中:
①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC=180°.能判定 AB∥CD的有 ( )
A.3 个 B.2 个 C.1 个 D.0 个
10.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角A=120°,第二次拐的角 B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是 ( )
A.120° B.130° C.140° D.150°
二、填空题(本大题5小题,每小题4分,共20分)
11.如图,当剪刀口∠AOB增大21°时,∠COD 增大 .
12.图形在平移时,下列特征中不发生改变的有 (可多选).
①图形的形状;②图形的位置;③线段的长度;④角的大小;⑤垂直关系;⑥平行关系.
13.如图,如果∠1=40°,∠2=100°,那么∠3= ,∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .
14.如图,一个宽度相等的纸条按如图所示方法折叠一下,则∠1= .
15.一货船沿北偏西 62°方向航行,后因避礁先向右拐28°,再向左拐28°,这时货船沿着 方向前进.
三、解答题(一)(本大题5 小题,每小题6分,共30分)
16.读句画图:如图,直线CD 与直线AB 相交于点C,根据下列语句画图.
(1)过点 P 作PQ∥CD,交AB 于点 Q; (2)过点 P 作 PR⊥CD,垂足为点 R.
17.如图,平移三角形ABC,使点 A 移到点 A',请在图中画出平移后的图形.
18.填空完成推理过程:
如图,已知DE∥BC,AB∥EF.求证:∠DEF=∠B.
证明:∵AB∥EF(已知),
∴∠DEF=∠ADE( ).
∵DE∥BC(已知),
∴∠ADE=∠B( ).
∴∠DEF=∠B(等量代换).
19.已知:如图, AC平分∠BCD,求. 的度数.
20.如图,已知,AB⊥BC,AD∥BC,∠BAC=∠D=60°.试判断直线AC与DE 的位置关系,并说明理由.
四、解答题(二)(本大题5 小题,每小题8分,共40分)
21.如图,E,F分别在AB,CD上, 与 互余, 求证:
22.如图,在三角形 ABC中,D,E,G分别为边AB,AC和BC上的点,DC 与EG 交于点F,已知 试判断直线 DE 与 BC 的位置关系,并说明理由.
23.如图,在三角形 ABC中, ,三角形 ABC沿AB 方向平移至三角形DEF,若
(1)求三角形ABC沿AB 方向平移的距离;
(2)求四边形 AEFC的周长.
24.如图,直线MN分别与直线AH,DG交于点B,F,且 的角平分线BE 交直线DG于点 E, 的角平分线 FC 交直线AH 于点 C.
(1)求证:
(2)若 求∠BED的度数.
25.已知:如图,AB∥CD,试解决下列问题:
(1)如图(1),
(2)如图(2),.
(3)如图((3),∠1+∠2+∠3+∠4= ;
(4)如图(4),试探究
第五章检测卷
1. C 2. A 3. C 4. A 5. C 6. A 7. C 8. B 9. C10. D 11.21° 12.①③④⑤⑥
13.40° 80° 80°100°
14.65° 15.北偏西 62° 16.略 17.略
18.两直线平行,内错角相等 两直线平行,同位角相等
19.解:∵AD∥BC,
∴∠BCD=180°-∠D=80°.
∵AC平分∠BCD,
∴∠DAC=∠ACB=40°.
20.解: AC⊥DE,理由如下:
∵AB⊥BC,AD∥BC,
又∠BAC=60°,∴∠CAD=90°—60°=30°.
在三角形 ADF中, ∴AC⊥DE.
21.证明:∵ EC⊥AF(已知),
∴∠1与∠C 互余.
∵ AF∥ED(已知),
∴ ∠1=∠D(两直线平行,同位角相等).
∴ ∠D 与∠C互余.
∵∠2与∠C互余(已知),
∴∠2=∠D(等角的余角相等).
∴AB∥CD(内错角相等,两直线平行).
22.解:DE∥BC,理由如下:
∵∠1=60°,∴∠CFG=180°—∠1=120°.
∴AB∥EG.∴∠EGC=∠B.
又∠3=∠B,∴∠3=∠EGC.
∴DE∥BC.
23.解:(1)由平移的性质可得AD=BE.
∵AE=8cm ,DB=2cm,
即三角形ABC 沿AB 方向平移的距离为 3cm.
(2)由平移的性质可得CF=AD=3cm,EF=BC=3c m,
∴四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18(cm).
24.(1)证明:∵∠1=∠2,∠1=∠ABF,∠2=∠BFG,∴∠ABF=∠BFG.
∵∠ABF 的角平分线BE 交直线DG 于点E,∠BFG的角平分线FC 交直线AH 于点C,
∴∠EBF=∠CFB.∴BE∥CF.
(2)解:由(1)得 BE∥CF. AH∥DG,∴∠ABE=∠BCF=35°,∠BED=180°-∠ABE=145°.
25.(1)180° (2)360° (3)540° (4)(n-1)·180°
(90分钟 120分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.体育课上,老师测量跳远成绩的依据是 ( )
A.平行线间的距离相等 B.两点之间,线段最短
C.垂线段最短 D.两点确定一条直线
2.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是 ( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角互补,两直线平行 D.两直线平行,同位角相等
3.如图,已知直线AB∥CD, ∠C=115°,∠A=25°,则∠E= ( )
A.70° B.80° C.90° D.100°
4.如图,若∠1=60°,∠2=120°,∠3=60°,则有 ( )
A.a∥b B.c∥d
C. a⊥d D.无法判定任意两条直线是否平行
5.一副三角板按如图方式摆放,且∠1的度数是∠2度数的4 倍,则∠1= ( )
A.18° B.54° C.72° D.70°
6.如图所示的四个图形中,∠1 与∠2是对顶角的图形有 ( )
A.1个 B.2 个 C.3个 D.4个
7.如图,BE平分∠ABC,DE∥BC,图中相等的角共有 ( )
A.3 对 B.4 对 C.5 对 D.6 对
8.如图,把一张长方形的纸片沿着 EF折叠,点 C,D 分别落在M,N 的位置,且 则∠AEN= ( )
中小学教育资源及组卷应用平台
A.30° B.36° C.45° D.72°
9.如图,在下列条件中:
①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC=180°.能判定 AB∥CD的有 ( )
A.3 个 B.2 个 C.1 个 D.0 个
10.如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的角A=120°,第二次拐的角 B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是 ( )
A.120° B.130° C.140° D.150°
二、填空题(本大题5小题,每小题4分,共20分)
11.如图,当剪刀口∠AOB增大21°时,∠COD 增大 .
12.图形在平移时,下列特征中不发生改变的有 (可多选).
①图形的形状;②图形的位置;③线段的长度;④角的大小;⑤垂直关系;⑥平行关系.
13.如图,如果∠1=40°,∠2=100°,那么∠3= ,∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .
14.如图,一个宽度相等的纸条按如图所示方法折叠一下,则∠1= .
15.一货船沿北偏西 62°方向航行,后因避礁先向右拐28°,再向左拐28°,这时货船沿着 方向前进.
三、解答题(一)(本大题5 小题,每小题6分,共30分)
16.读句画图:如图,直线CD 与直线AB 相交于点C,根据下列语句画图.
(1)过点 P 作PQ∥CD,交AB 于点 Q; (2)过点 P 作 PR⊥CD,垂足为点 R.
17.如图,平移三角形ABC,使点 A 移到点 A',请在图中画出平移后的图形.
18.填空完成推理过程:
如图,已知DE∥BC,AB∥EF.求证:∠DEF=∠B.
证明:∵AB∥EF(已知),
∴∠DEF=∠ADE( ).
∵DE∥BC(已知),
∴∠ADE=∠B( ).
∴∠DEF=∠B(等量代换).
19.已知:如图, AC平分∠BCD,求. 的度数.
20.如图,已知,AB⊥BC,AD∥BC,∠BAC=∠D=60°.试判断直线AC与DE 的位置关系,并说明理由.
四、解答题(二)(本大题5 小题,每小题8分,共40分)
21.如图,E,F分别在AB,CD上, 与 互余, 求证:
22.如图,在三角形 ABC中,D,E,G分别为边AB,AC和BC上的点,DC 与EG 交于点F,已知 试判断直线 DE 与 BC 的位置关系,并说明理由.
23.如图,在三角形 ABC中, ,三角形 ABC沿AB 方向平移至三角形DEF,若
(1)求三角形ABC沿AB 方向平移的距离;
(2)求四边形 AEFC的周长.
24.如图,直线MN分别与直线AH,DG交于点B,F,且 的角平分线BE 交直线DG于点 E, 的角平分线 FC 交直线AH 于点 C.
(1)求证:
(2)若 求∠BED的度数.
25.已知:如图,AB∥CD,试解决下列问题:
(1)如图(1),
(2)如图(2),.
(3)如图((3),∠1+∠2+∠3+∠4= ;
(4)如图(4),试探究
第五章检测卷
1. C 2. A 3. C 4. A 5. C 6. A 7. C 8. B 9. C10. D 11.21° 12.①③④⑤⑥
13.40° 80° 80°100°
14.65° 15.北偏西 62° 16.略 17.略
18.两直线平行,内错角相等 两直线平行,同位角相等
19.解:∵AD∥BC,
∴∠BCD=180°-∠D=80°.
∵AC平分∠BCD,
∴∠DAC=∠ACB=40°.
20.解: AC⊥DE,理由如下:
∵AB⊥BC,AD∥BC,
又∠BAC=60°,∴∠CAD=90°—60°=30°.
在三角形 ADF中, ∴AC⊥DE.
21.证明:∵ EC⊥AF(已知),
∴∠1与∠C 互余.
∵ AF∥ED(已知),
∴ ∠1=∠D(两直线平行,同位角相等).
∴ ∠D 与∠C互余.
∵∠2与∠C互余(已知),
∴∠2=∠D(等角的余角相等).
∴AB∥CD(内错角相等,两直线平行).
22.解:DE∥BC,理由如下:
∵∠1=60°,∴∠CFG=180°—∠1=120°.
∴AB∥EG.∴∠EGC=∠B.
又∠3=∠B,∴∠3=∠EGC.
∴DE∥BC.
23.解:(1)由平移的性质可得AD=BE.
∵AE=8cm ,DB=2cm,
即三角形ABC 沿AB 方向平移的距离为 3cm.
(2)由平移的性质可得CF=AD=3cm,EF=BC=3c m,
∴四边形AEFC的周长=AE+EF+CF+AC=8+3+3+4=18(cm).
24.(1)证明:∵∠1=∠2,∠1=∠ABF,∠2=∠BFG,∴∠ABF=∠BFG.
∵∠ABF 的角平分线BE 交直线DG 于点E,∠BFG的角平分线FC 交直线AH 于点C,
∴∠EBF=∠CFB.∴BE∥CF.
(2)解:由(1)得 BE∥CF. AH∥DG,∴∠ABE=∠BCF=35°,∠BED=180°-∠ABE=145°.
25.(1)180° (2)360° (3)540° (4)(n-1)·180°
