人教版七年级下册期中检测卷(含答案)
文档属性
| 名称 | 人教版七年级下册期中检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 651.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 09:48:19 | ||
图片预览


文档简介
期中检测卷
(90分钟 120分)
一、选择题(本大题10 小题,每小题3分,共30分)
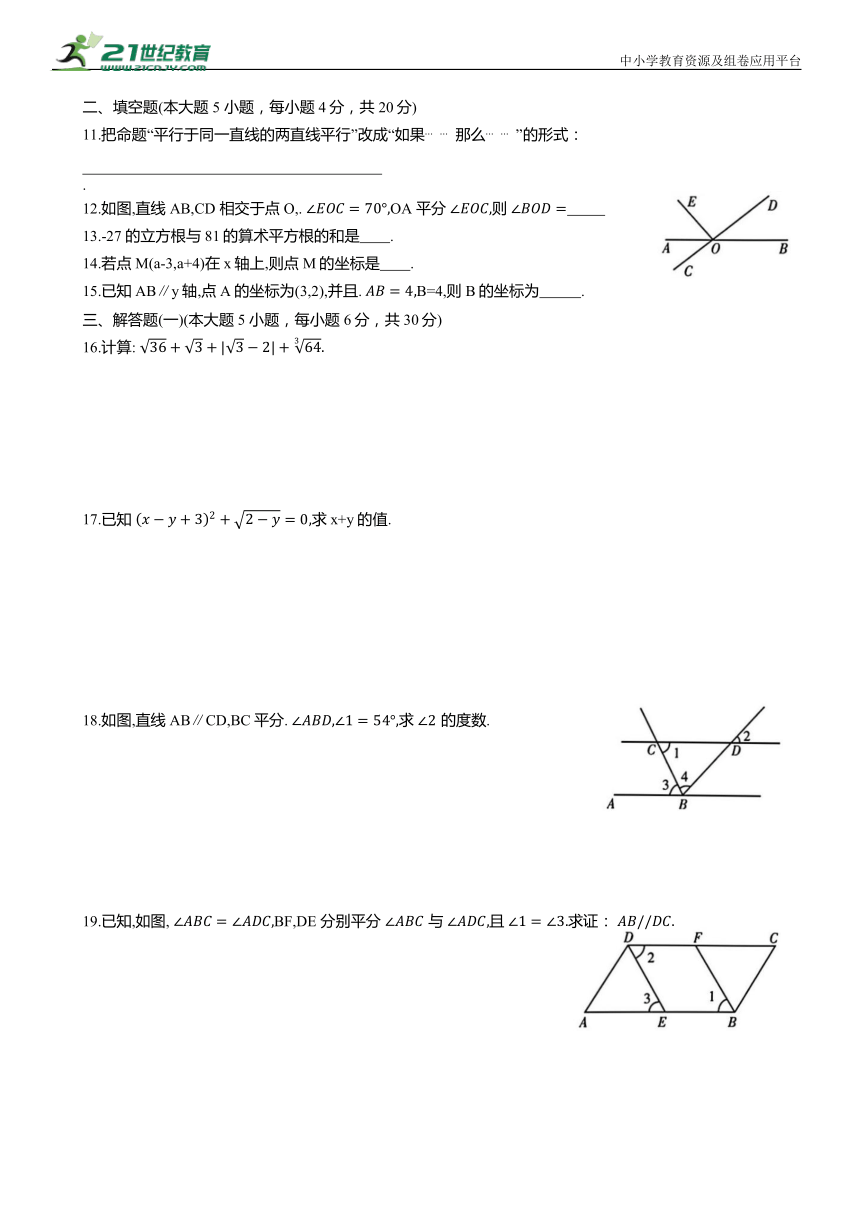
1.如图,∠1=50°,则∠2= ( )
A.100° B.120° C.130° D.140°
2.实数 的相反数是 ( )
B.
3.下列实数中的无理数为 ( )
A.0.53 D.π/2
4.下列各组数互为相反数的是 ( )
A.-2与0.5 与
与 与
5.如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是 ( )
A.∠1=∠2 B.∠3=∠4
C.∠A=∠5 D.∠A+∠ABC=180°
6.一个正数的两个平方根分别是2a--1与--a+2,则a的值为 ( )
A.-1 B.1 C.2 D.-2
7.点A 在平面直角坐标系中的坐标是(3,-4),则点A到y 轴的距离是 ( )
A.3 B.-4 C.4 D.-3
8.将A(-4,1)先向右平移5个单位长度,再向上平移2个单位长度,平移后点的坐标是 ( )
A.(-9,3) B.(1,3) C.(-9,-1) D.(1,-1)
9.某中学 2018届新生入学军训时,小华、小军、小刚的位置如图所示,如果小军的位置用(0,0)表示,小刚的位置用(2,2)表示,那么小华的位置可表示为 ( )
A.(-2,-1) B.(-1,-2) C.(2,1) D.(1,2)
10.已知 与5x"y是同类项,则m 与n 的值分别是 ( )
中小学教育资源及组卷应用平台
A.4,1 B.1,4 C.0,8 D.8,0
二、填空题(本大题5 小题,每小题4分,共20分)
11.把命题“平行于同一直线的两直线平行”改成“如果 那么 ”的形式:
.
12.如图,直线 AB,CD 相交于点O,. OA 平分 则
13.-27 的立方根与81的算术平方根的和是 .
14.若点M(a-3,a+4)在x轴上,则点 M的坐标是 .
15.已知AB∥y轴,点 A的坐标为(3,2),并且. B=4,则B的坐标为 .
三、解答题(一)(本大题5 小题,每小题6分,共30分)
16.计算:
17.已知 求x+y的值.
18.如图,直线AB∥CD,BC平分. 求 的度数.
19.已知,如图, BF,DE 分别平分 与 且 求证:
20.已知 的平方根是: 的平方根是: 求 的立方根.
四、解答题(二)(本大题5 小题,每小题8分,共40分)
21.如图,已知. BE平分.
(1)求 的度数;
(2)判断 BE 与AC 的位置关系,并说明理由.
22.如图,三角形ABC三个顶点A,B,C 的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形 向右平移4 个单位长度,再向下平移3个单位长度,恰好得到三角形 ABC,试写出三角形 三个顶点的坐标;
(2)求三角形ABC的面积.
23.小丽想在一块面积为 的正方形纸片上,沿着边的方向裁出一块面积为 的长方形纸片,并且使它的长宽的比为2:1.问:小丽能否用这块正方形纸片裁出符合要求的长方形纸片 为什么
24.如图1,长方形 ABCD 的边AB 在数轴上,点 A 与原点O重合,AB边长为4.将长方形 ABCD 沿数轴向右水平移动,移动后的长方形记为
(1)当数轴上点 表示的数是2时,数轴上点. 表示的数为 ;
(2)若移动后的长方形 与原长方形ABCD 的重叠部分(如图 2 中阴影部分)恰好是面积为7的正方形时,试求点 B'表示的数并判断它在哪两个相邻的整数之间.
25.问题情境:如图(1), 求 的度数.
小明的思路是:过 P 作. 通过平行线性质来求.
(1)按小明的思路,易求得 的度数为 ;
(2)问题迁移:如图(2), 点 P 在射线OM 上运动,记 ,当点 P 在B,D两点之间运动时,问. 与α,β之间有何数量关系 请说明理由;
(3)在(2)的条件下,如果点P在B,D两点外侧运动时(点 P 与点O,B,D三点不重合),请直接写出 与α,β之间的数量关系.
期中检测卷
1. C 2. A 3. D 4. B 5. B 6. A 7. A 8. B 9. A10. B
11.如果两条直线都与第三条直线平行,那么这两条直线互相平行
12.35° 13.6 14.(-7,0) 15.(3,-2)或(3,6)
16.12 17.1
18.解:∵直线AB∥CD,
∴∠1=∠3=54°,∠ABD+∠BDC=180°.
∵BC平分∠ABD,
∴∠3=∠4=54°.
19.证明:∵BF,DE分别平分∠ABC与∠ADC,
∴∠ABC=2∠1,∠ADC=2∠2.
∵∠ABC=∠ADC,∴∠1=∠2.
∵∠1=∠3,∴∠2=∠3.
∴AB∥CD.
21.解:(1)∵BE平分∠ABC,且∠ABC=50°,
∵DE∥BC,
∴∠BED=∠EBC=25°.
(2)BE⊥AC,理由如下:
∵DE∥BC,且∠C=65°,
∴∠AED=∠C=65°.
∵∠BED=25°,
∴∠AEB=∠AED+∠BED=65°+25°=90°.
∴BE⊥AC.
22.(1)A (-3.5),B (0.6),C (-1,4).
(2)三角形ABC的面积
=6--1-1--1.5
=2.5.
23.解:设长方形纸片的长为2xcm,宽为 x cm,则2x·x=30.解得.
则长方形纸片的长为
因为 而正方形纸片的边长为 所以不能裁剪出符合要求的长方形.
24.(1)6 (2)点 B'表示的数为 在5,6之间.
25.解:(1)110°
(2)∠APC=α+β.
理由如下:如图,过 P作PE∥AB交AC 于点E,
∵AB∥CD,∴AB∥PE∥CD.
∴α=∠APE,β=∠CPE.
∴∠APC=∠APE+∠CPE=α+β.
(3)如图,当 P 在 BD 延长线上时,∠CPA=α-β.
如图,当 P 在DB 延长线上时,∠CPA=β-α.
(90分钟 120分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.如图,∠1=50°,则∠2= ( )
A.100° B.120° C.130° D.140°
2.实数 的相反数是 ( )
B.
3.下列实数中的无理数为 ( )
A.0.53 D.π/2
4.下列各组数互为相反数的是 ( )
A.-2与0.5 与
与 与
5.如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是 ( )
A.∠1=∠2 B.∠3=∠4
C.∠A=∠5 D.∠A+∠ABC=180°
6.一个正数的两个平方根分别是2a--1与--a+2,则a的值为 ( )
A.-1 B.1 C.2 D.-2
7.点A 在平面直角坐标系中的坐标是(3,-4),则点A到y 轴的距离是 ( )
A.3 B.-4 C.4 D.-3
8.将A(-4,1)先向右平移5个单位长度,再向上平移2个单位长度,平移后点的坐标是 ( )
A.(-9,3) B.(1,3) C.(-9,-1) D.(1,-1)
9.某中学 2018届新生入学军训时,小华、小军、小刚的位置如图所示,如果小军的位置用(0,0)表示,小刚的位置用(2,2)表示,那么小华的位置可表示为 ( )
A.(-2,-1) B.(-1,-2) C.(2,1) D.(1,2)
10.已知 与5x"y是同类项,则m 与n 的值分别是 ( )
中小学教育资源及组卷应用平台
A.4,1 B.1,4 C.0,8 D.8,0
二、填空题(本大题5 小题,每小题4分,共20分)
11.把命题“平行于同一直线的两直线平行”改成“如果 那么 ”的形式:
.
12.如图,直线 AB,CD 相交于点O,. OA 平分 则
13.-27 的立方根与81的算术平方根的和是 .
14.若点M(a-3,a+4)在x轴上,则点 M的坐标是 .
15.已知AB∥y轴,点 A的坐标为(3,2),并且. B=4,则B的坐标为 .
三、解答题(一)(本大题5 小题,每小题6分,共30分)
16.计算:
17.已知 求x+y的值.
18.如图,直线AB∥CD,BC平分. 求 的度数.
19.已知,如图, BF,DE 分别平分 与 且 求证:
20.已知 的平方根是: 的平方根是: 求 的立方根.
四、解答题(二)(本大题5 小题,每小题8分,共40分)
21.如图,已知. BE平分.
(1)求 的度数;
(2)判断 BE 与AC 的位置关系,并说明理由.
22.如图,三角形ABC三个顶点A,B,C 的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形 向右平移4 个单位长度,再向下平移3个单位长度,恰好得到三角形 ABC,试写出三角形 三个顶点的坐标;
(2)求三角形ABC的面积.
23.小丽想在一块面积为 的正方形纸片上,沿着边的方向裁出一块面积为 的长方形纸片,并且使它的长宽的比为2:1.问:小丽能否用这块正方形纸片裁出符合要求的长方形纸片 为什么
24.如图1,长方形 ABCD 的边AB 在数轴上,点 A 与原点O重合,AB边长为4.将长方形 ABCD 沿数轴向右水平移动,移动后的长方形记为
(1)当数轴上点 表示的数是2时,数轴上点. 表示的数为 ;
(2)若移动后的长方形 与原长方形ABCD 的重叠部分(如图 2 中阴影部分)恰好是面积为7的正方形时,试求点 B'表示的数并判断它在哪两个相邻的整数之间.
25.问题情境:如图(1), 求 的度数.
小明的思路是:过 P 作. 通过平行线性质来求.
(1)按小明的思路,易求得 的度数为 ;
(2)问题迁移:如图(2), 点 P 在射线OM 上运动,记 ,当点 P 在B,D两点之间运动时,问. 与α,β之间有何数量关系 请说明理由;
(3)在(2)的条件下,如果点P在B,D两点外侧运动时(点 P 与点O,B,D三点不重合),请直接写出 与α,β之间的数量关系.
期中检测卷
1. C 2. A 3. D 4. B 5. B 6. A 7. A 8. B 9. A10. B
11.如果两条直线都与第三条直线平行,那么这两条直线互相平行
12.35° 13.6 14.(-7,0) 15.(3,-2)或(3,6)
16.12 17.1
18.解:∵直线AB∥CD,
∴∠1=∠3=54°,∠ABD+∠BDC=180°.
∵BC平分∠ABD,
∴∠3=∠4=54°.
19.证明:∵BF,DE分别平分∠ABC与∠ADC,
∴∠ABC=2∠1,∠ADC=2∠2.
∵∠ABC=∠ADC,∴∠1=∠2.
∵∠1=∠3,∴∠2=∠3.
∴AB∥CD.
21.解:(1)∵BE平分∠ABC,且∠ABC=50°,
∵DE∥BC,
∴∠BED=∠EBC=25°.
(2)BE⊥AC,理由如下:
∵DE∥BC,且∠C=65°,
∴∠AED=∠C=65°.
∵∠BED=25°,
∴∠AEB=∠AED+∠BED=65°+25°=90°.
∴BE⊥AC.
22.(1)A (-3.5),B (0.6),C (-1,4).
(2)三角形ABC的面积
=6--1-1--1.5
=2.5.
23.解:设长方形纸片的长为2xcm,宽为 x cm,则2x·x=30.解得.
则长方形纸片的长为
因为 而正方形纸片的边长为 所以不能裁剪出符合要求的长方形.
24.(1)6 (2)点 B'表示的数为 在5,6之间.
25.解:(1)110°
(2)∠APC=α+β.
理由如下:如图,过 P作PE∥AB交AC 于点E,
∵AB∥CD,∴AB∥PE∥CD.
∴α=∠APE,β=∠CPE.
∴∠APC=∠APE+∠CPE=α+β.
(3)如图,当 P 在 BD 延长线上时,∠CPA=α-β.
如图,当 P 在DB 延长线上时,∠CPA=β-α.
同课章节目录
