第七章平面直角坐标系检测卷(含答案)
文档属性
| 名称 | 第七章平面直角坐标系检测卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 893.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 09:45:18 | ||
图片预览


文档简介
第七章平面直角坐标系检测卷
(90 分钟 120分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.如图所示,PA=3,PB=2,则点 P的坐标为 ( )
A.(2,3) B.(3,2) C.(-2,3) D.(-3,2)
2.如图,下列说法正确的是 ( )
A. A 与 D 的横坐标相同 B. C 与D 的横坐标相同
C. B 与C 的纵坐标相同 D. B 与 D 的纵坐标相同
3.若x轴上的点 P 到y 轴的距离为 3,则点 P 的坐标为 ( )
A.(3,0) B.(3,0)或(-3,0) C.(0,3) D.(0,3)或(0,-3)
4.如果点 P(5,y)在第四象限,那么y的取值范围是 ( )
A. y<0 B. y>0 C.y≤o D. y≥0
5.线段CD 是由线段AB 平移得到的,点A(-1,4)的对应点为C(4,7),则点 B(-4,--1)的对应点 D的坐标为 ( )
A.(2,9) B.(5,3) C.(1,2) D.(- 9,- 4)
6.一个长方形在平面直角坐标系中三个顶点的坐标为(--1,--1),(--1,2),(3,--1),则第四个顶点的坐标为 ( )
A.(2,2) B.(3,2) C.(3,3) D.(2,3)
7.已知点 P(a,b), ab>0,a+b<0,则点 P 在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.点 P(m+3,m+1)在直角坐标系的x轴上,则点 P 坐标为 ( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
9.已知点 M在第二象限,它到x轴距离为3,到y轴距离为2,则点 M的坐标为 ( )
A.(3,-2) B.(2,-3) C.(-2,3) D.(-3,2)
10.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比( )
A.向右平移了3个单位长度 B.向左平移了 3 个单位长度
C.向上平移了 3个单位长度 D.向下平移了 3 个单位长度
二、填空题(本大题5 小题,每小题4分,共20分)
11.点A 在x 轴上,位于原点的右侧,距离坐标原点5个单位长度,则此点的坐标为 ;点 B 在y 轴上,位于原点的下方,距离坐标原点5个单位长度,则此点的坐标为 ;点 C 在y 轴左侧,在x轴下方,距离每个坐标轴都是5个单位长度,则此点的坐标为 .
12.某人从火车站向南走300米到平价超市,再从平价超市向西走 100米,再向北走500米到汽车站,若以火车站为坐标原点建立平面直角坐标系,以正东、正北方向分别为x轴、y轴的正方向,平价超市的坐标为(0,--300),则汽车站的坐标为 .
13.小华将平面直角坐标系中的猫的图案向右平移了3个单位长度,平移前猫眼的坐标为(--4,3),(--2,3),则移动后猫眼的坐标为 .
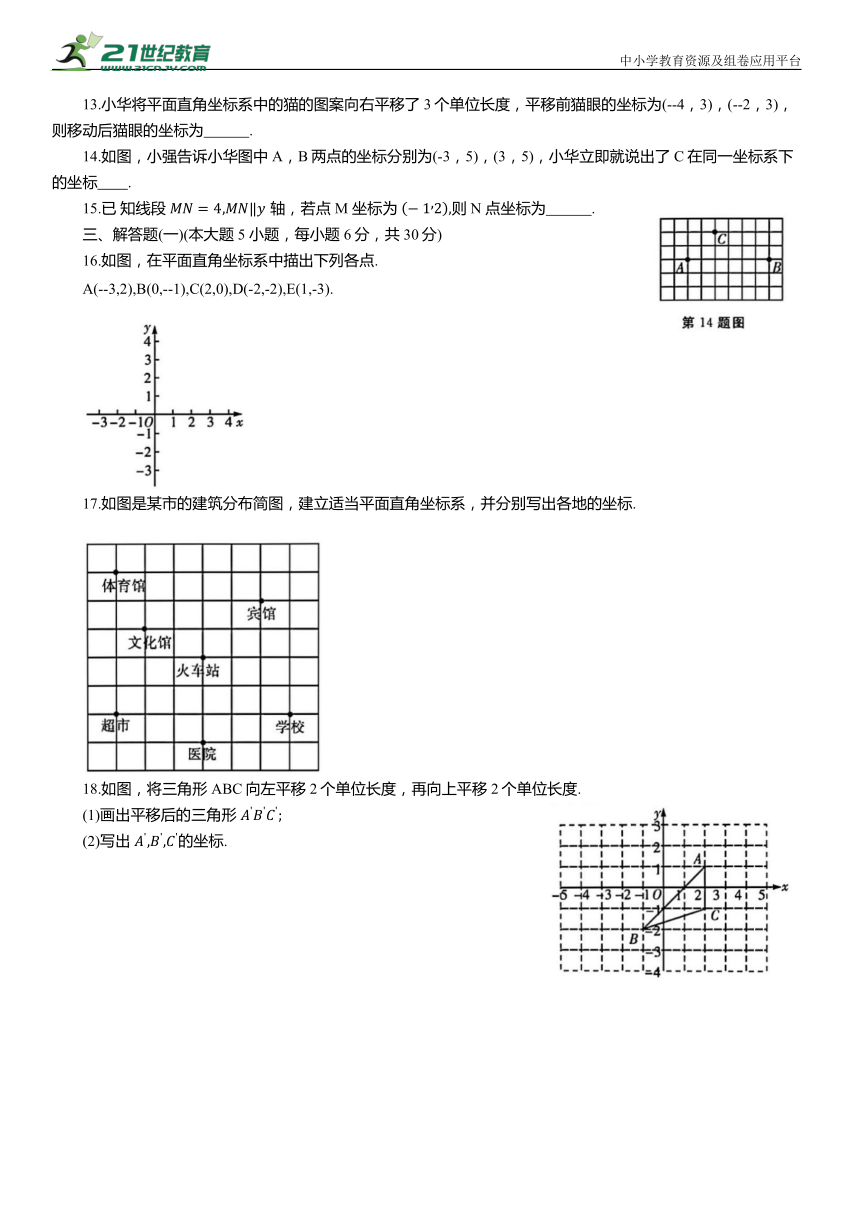
14.如图,小强告诉小华图中A,B两点的坐标分别为(-3,5),(3,5),小华立即就说出了C在同一坐标系下的坐标 .
15.已 知线段 轴,若点 M 坐标为 则 N 点坐标为 .
三、解答题(一)(本大题5 小题,每小题6分,共30分)
16.如图,在平面直角坐标系中描出下列各点.
A(--3,2),B(0,--1),C(2,0),D(-2,-2),E(1,-3).
17.如图是某市的建筑分布简图,建立适当平面直角坐标系,并分别写出各地的坐标.
18.如图,将三角形ABC向左平移2个单位长度,再向上平移2个单位长度.
(1)画出平移后的三角形
中小学教育资源及组卷应用平台
(2)写出 的坐标.
19.如图,在四边形ABCD 中, ,写出A,B,C,D 四点的坐标.
20.若线段AB 平行于x 轴,AB的长为4,且A 的坐标为(2,3),求点 B 的坐标.
四、解答题(二)(本大题5 小题,每小题8分,共40分)
21.如图,在平面直角坐标系中,标出下列各点:
(1)点 A 在x轴的正半轴上,距离原点 1 个单位长度;
(2)点 B 在y轴的负半轴上,距离原点 2个单位长度;
(3)点C在第四象限,距离x轴1个单位长度,距离y轴3个单位长度;
(4)点D在第一象限,距离x轴1个单位长度,距离y轴4个单位长度.
请用线段依次连接这些点,你能得到什么图形
22.如图,在长方形OABC中,点 A 坐标为( 点 B坐标为( 点 C 坐标为(0,2).
(1)将长方形顶点O,A,B,C四点横,纵坐标同乘 ,得到长方形 请画出图形,并写出 的坐标;
(2)若点 P (x,y)在 BC边上,则. 在什么位置
23.如图,在平面直角坐标系中,正方形ABCD 和正方形EFGC 的面积分别为64和16.
(1)请写出点 A,E,F的坐标;
(2)求三角形 BDF的面积.
24.如图,点 C(-3,1),D(0,2).
(1)在x轴上找一点 P,使. 并写出 P 点坐标;
(2)在y轴上找一点Q,使三角形QCD为等腰三角形,画出Q点位置并写出满足Q 点的一个坐标.
25.如图是某台阶的一部分,如果A 点的坐标为(0,0),B 点的坐标为(1,1).
(1)请建立适当的平面直角坐标系,并写出其余各点的坐标;
(2)如果台阶有10级,请你求出该台阶的长度和高度;
(3)若这10级台阶的宽度都是2m,单位长度为1m,现要将这些台阶铺上地毯,需要多少平方米
第七章检测卷
1. C 2. C 3. B 4. A 5. C 6. B 7. C 8. B 9. C10. D 11.(5.0) (0,—5) (-5,—5)
12.(-100,200) 13.(-1,3),(1,3) 14.(-1,7)
15.(-1,6) (-1,-2)
16.略 17.略
18.(1)略(2)A'(0,3),B'(-3,0). C'(0.1)
19.解:A(0,0),
∵AB=2,∴B(2,0).
∵DE=1,AE=1.5,CD=4,
∴CE=CD-DE=3.
∴C(3,1.5),D(-1,1.5).
20.解:∵线段AB平行于x轴,A 的坐标为(2,3),
∴点 B的纵坐标是 3.
∵AB=4,
∴点 B 在点A 的左边时,横坐标为2-4=-2,点 B在点A 的右边时,横坐标为2+4=6.
∴点 B 的坐标为(6.3)或(-2,3).
21.解:(1)(2)(3)(4)如图.
用线段依次连接这些点,得到一个平行四边形.
22.解:(1)如图,
O (0,0),A (3,0),B (3,-2),C (0,-2).
(2)∵点 P (x,y)在BC边上,
在 B C 上且在直线 P O 与 B C 的交点处.
23.解:(1)∵正方形ABCD 和正方形EFGC 面积分别为64 和16,
∴正方形 ABCD 和正方形 EFGC 的边长分别为 8和 4.
∴OG=8+4=12.
∴A(0,8),E(8,4),F(12,4).
=32+24-24
=32.
24.解:(1)∵C(-3,1),D(0,2),PC=PD,∴在x轴上点P 的坐标是(-1,0).
(2)分别以C,D为圆心,CD长为半径画弧与y 轴相交,过CD的中点作CD 的垂线与y轴相交,可得4个满足题意的点 Q,图略.其中一个点 Q为原点(0,0).
25.解:(1)建立平面直角坐标系如图所示,
C(2,2),D(3,3),E(4,4),F(5.5).
(2)台阶的长度:1×(10+1)=11,
高度:1×10=10.
(3)∵单位长度为1m.
∴地毯的长度为:(11+10)×1=21m.
∵台阶的宽度都是2m,
∴地毯的面积为
答:将这些台阶铺上地毯,需要42平方米.
(90 分钟 120分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.如图所示,PA=3,PB=2,则点 P的坐标为 ( )
A.(2,3) B.(3,2) C.(-2,3) D.(-3,2)
2.如图,下列说法正确的是 ( )
A. A 与 D 的横坐标相同 B. C 与D 的横坐标相同
C. B 与C 的纵坐标相同 D. B 与 D 的纵坐标相同
3.若x轴上的点 P 到y 轴的距离为 3,则点 P 的坐标为 ( )
A.(3,0) B.(3,0)或(-3,0) C.(0,3) D.(0,3)或(0,-3)
4.如果点 P(5,y)在第四象限,那么y的取值范围是 ( )
A. y<0 B. y>0 C.y≤o D. y≥0
5.线段CD 是由线段AB 平移得到的,点A(-1,4)的对应点为C(4,7),则点 B(-4,--1)的对应点 D的坐标为 ( )
A.(2,9) B.(5,3) C.(1,2) D.(- 9,- 4)
6.一个长方形在平面直角坐标系中三个顶点的坐标为(--1,--1),(--1,2),(3,--1),则第四个顶点的坐标为 ( )
A.(2,2) B.(3,2) C.(3,3) D.(2,3)
7.已知点 P(a,b), ab>0,a+b<0,则点 P 在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.点 P(m+3,m+1)在直角坐标系的x轴上,则点 P 坐标为 ( )
A.(0,-2) B.(2,0) C.(4,0) D.(0,-4)
9.已知点 M在第二象限,它到x轴距离为3,到y轴距离为2,则点 M的坐标为 ( )
A.(3,-2) B.(2,-3) C.(-2,3) D.(-3,2)
10.在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比( )
A.向右平移了3个单位长度 B.向左平移了 3 个单位长度
C.向上平移了 3个单位长度 D.向下平移了 3 个单位长度
二、填空题(本大题5 小题,每小题4分,共20分)
11.点A 在x 轴上,位于原点的右侧,距离坐标原点5个单位长度,则此点的坐标为 ;点 B 在y 轴上,位于原点的下方,距离坐标原点5个单位长度,则此点的坐标为 ;点 C 在y 轴左侧,在x轴下方,距离每个坐标轴都是5个单位长度,则此点的坐标为 .
12.某人从火车站向南走300米到平价超市,再从平价超市向西走 100米,再向北走500米到汽车站,若以火车站为坐标原点建立平面直角坐标系,以正东、正北方向分别为x轴、y轴的正方向,平价超市的坐标为(0,--300),则汽车站的坐标为 .
13.小华将平面直角坐标系中的猫的图案向右平移了3个单位长度,平移前猫眼的坐标为(--4,3),(--2,3),则移动后猫眼的坐标为 .
14.如图,小强告诉小华图中A,B两点的坐标分别为(-3,5),(3,5),小华立即就说出了C在同一坐标系下的坐标 .
15.已 知线段 轴,若点 M 坐标为 则 N 点坐标为 .
三、解答题(一)(本大题5 小题,每小题6分,共30分)
16.如图,在平面直角坐标系中描出下列各点.
A(--3,2),B(0,--1),C(2,0),D(-2,-2),E(1,-3).
17.如图是某市的建筑分布简图,建立适当平面直角坐标系,并分别写出各地的坐标.
18.如图,将三角形ABC向左平移2个单位长度,再向上平移2个单位长度.
(1)画出平移后的三角形
中小学教育资源及组卷应用平台
(2)写出 的坐标.
19.如图,在四边形ABCD 中, ,写出A,B,C,D 四点的坐标.
20.若线段AB 平行于x 轴,AB的长为4,且A 的坐标为(2,3),求点 B 的坐标.
四、解答题(二)(本大题5 小题,每小题8分,共40分)
21.如图,在平面直角坐标系中,标出下列各点:
(1)点 A 在x轴的正半轴上,距离原点 1 个单位长度;
(2)点 B 在y轴的负半轴上,距离原点 2个单位长度;
(3)点C在第四象限,距离x轴1个单位长度,距离y轴3个单位长度;
(4)点D在第一象限,距离x轴1个单位长度,距离y轴4个单位长度.
请用线段依次连接这些点,你能得到什么图形
22.如图,在长方形OABC中,点 A 坐标为( 点 B坐标为( 点 C 坐标为(0,2).
(1)将长方形顶点O,A,B,C四点横,纵坐标同乘 ,得到长方形 请画出图形,并写出 的坐标;
(2)若点 P (x,y)在 BC边上,则. 在什么位置
23.如图,在平面直角坐标系中,正方形ABCD 和正方形EFGC 的面积分别为64和16.
(1)请写出点 A,E,F的坐标;
(2)求三角形 BDF的面积.
24.如图,点 C(-3,1),D(0,2).
(1)在x轴上找一点 P,使. 并写出 P 点坐标;
(2)在y轴上找一点Q,使三角形QCD为等腰三角形,画出Q点位置并写出满足Q 点的一个坐标.
25.如图是某台阶的一部分,如果A 点的坐标为(0,0),B 点的坐标为(1,1).
(1)请建立适当的平面直角坐标系,并写出其余各点的坐标;
(2)如果台阶有10级,请你求出该台阶的长度和高度;
(3)若这10级台阶的宽度都是2m,单位长度为1m,现要将这些台阶铺上地毯,需要多少平方米
第七章检测卷
1. C 2. C 3. B 4. A 5. C 6. B 7. C 8. B 9. C10. D 11.(5.0) (0,—5) (-5,—5)
12.(-100,200) 13.(-1,3),(1,3) 14.(-1,7)
15.(-1,6) (-1,-2)
16.略 17.略
18.(1)略(2)A'(0,3),B'(-3,0). C'(0.1)
19.解:A(0,0),
∵AB=2,∴B(2,0).
∵DE=1,AE=1.5,CD=4,
∴CE=CD-DE=3.
∴C(3,1.5),D(-1,1.5).
20.解:∵线段AB平行于x轴,A 的坐标为(2,3),
∴点 B的纵坐标是 3.
∵AB=4,
∴点 B 在点A 的左边时,横坐标为2-4=-2,点 B在点A 的右边时,横坐标为2+4=6.
∴点 B 的坐标为(6.3)或(-2,3).
21.解:(1)(2)(3)(4)如图.
用线段依次连接这些点,得到一个平行四边形.
22.解:(1)如图,
O (0,0),A (3,0),B (3,-2),C (0,-2).
(2)∵点 P (x,y)在BC边上,
在 B C 上且在直线 P O 与 B C 的交点处.
23.解:(1)∵正方形ABCD 和正方形EFGC 面积分别为64 和16,
∴正方形 ABCD 和正方形 EFGC 的边长分别为 8和 4.
∴OG=8+4=12.
∴A(0,8),E(8,4),F(12,4).
=32+24-24
=32.
24.解:(1)∵C(-3,1),D(0,2),PC=PD,∴在x轴上点P 的坐标是(-1,0).
(2)分别以C,D为圆心,CD长为半径画弧与y 轴相交,过CD的中点作CD 的垂线与y轴相交,可得4个满足题意的点 Q,图略.其中一个点 Q为原点(0,0).
25.解:(1)建立平面直角坐标系如图所示,
C(2,2),D(3,3),E(4,4),F(5.5).
(2)台阶的长度:1×(10+1)=11,
高度:1×10=10.
(3)∵单位长度为1m.
∴地毯的长度为:(11+10)×1=21m.
∵台阶的宽度都是2m,
∴地毯的面积为
答:将这些台阶铺上地毯,需要42平方米.
