5.3 平行线的性质课时同步练习(含答案)
文档属性
| 名称 | 5.3 平行线的性质课时同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 900.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 09:50:35 | ||
图片预览





文档简介
5.3 平行线的性质课时同步练习
第 1课时 平行线的性质
基础知识夯实
知识沉淀
平行线的性质:
平行线的性质 性质1 性质2 性质3
语言描述 两 直线 平 行,同位角______ 两 直 线 平 行,内错角______ 两直线平行,同旁内角_____
图例
几何语言 ________,
基础过关
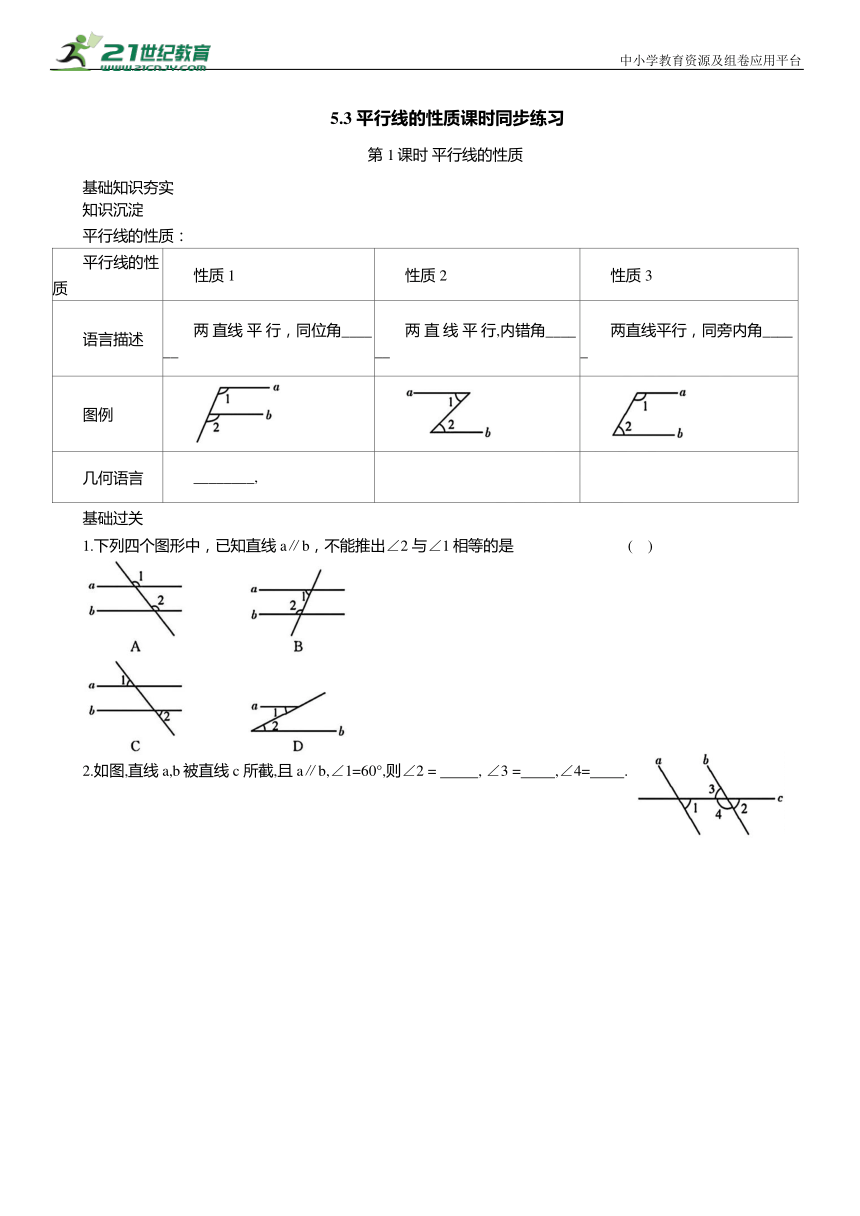
1.下列四个图形中,已知直线a∥b,不能推出∠2 与∠1相等的是 ( )
中小学教育资源及组卷应用平台
2.如图,直线a,b被直线c 所截,且a∥b,∠1=60°,则∠2 = , ∠3 = ,∠4= .
典型案例探究
【例题 1】如图,直线a∥b,直线 c 与a,b相交,∠1=70°,则∠2 的大小是 ( )
A.20° B.50° C.80° D.100°
【变式1】如图,直线 a∥b,∠1=60°,∠2=40°,则∠3等于 ( )
A.40° B.60
C.70° D.110°
知识点 2 两直线平行,内错角相等
【例题2】如图,直线l ∥l ,直线 l 与 l ,l 分别交于点A,C,BC⊥l 交l 于点 B,若∠1=70°,则∠2 的度数为
A.10° B.20°
C.30° D.40°
【变 式 2】如图, 已 知 BE 平 分∠ABC,且 BE∥DC,若∠ABC=50°,则∠C的度数是 ( )
A.20° B.25°
C.30° D.50°
知识点 3 两直线平行,同旁内角互补
【例题3】如图,AB∥CD,AD∥BC,请说明∠A=∠C.
【变式3】如图,直线 AB∥CD,直线 MN 分别交AB,CD于点E,F,EG平分∠BEF,交 CD 于点 G,若∠EFG=72°,求∠MEG的度数.
课后作业
A 组
1.如图,用一吸管吮易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2= .
2.如图,直线 AB,CD 被直线AE所截,AB∥CD,∠A=110°,则∠1= .
3.如图,若AB∥CD,则下列结论一定成立的是( )
A.∠1=∠2 B. AD∥BC
C.∠B=∠D D.∠3=∠4
4.如图,已知直线a∥b,直线c∥d,∠1=110°,求∠2,∠3,∠4 的度数.
5.如图,∠B=∠C,AE∥BC.试说明:AE平分∠CAD.
6.如图,修高速公路需要开山洞,为节省时间,要在山两面A,B同时开工,在A 处测得洞的走向是北偏东76°12',那么在B处应按什么方向开口,才能使山洞准确接通 请说明其中的道理.
B 组
如图,将一副三角板和一张边线平行的纸条按如图所示方式摆放,两个三角板的一直角边重合,含 30°角的直角三角板的斜边与纸条一边重合,含 45°角的直角三角板的一个顶点在纸条的另一边上,则∠1的度数是 .
8.如图,已知
(1)若 求∠BED 的度数;
(2)请猜想 的度数,并说明理由.
C 组
9.如图①②,∠B,∠E的两边分别平行.
(1)在图①中,∠B 与∠E 有什么数量关系 为什么
(2)在图②中,∠B 与∠E 有什么数量关系 为什么
(3)由(1)(2)你能得出什么结论 用一句话概括你得到的结论.
第2课时 平行线的判定与性质的综合运用
基础知识夯实
知识沉淀
平行线的性质 图例 平行线的判定
(1)两直线平行,同位角_________, ∵a∥b, ∴∠1=∠2 ∵_________,两直线平行. ∵∠1=∠2,∴a∥b
(2)两直线平行,内错角________ ∵_______, ∴_______ 内错角_______,两直线平行. ∵_______, ∴_______
(3)两直线平行,同旁内角______ ∵_______, ∴__________ 同旁内角_______,两直线平行 同位角_______, ∴_______
基础过关
1.如图,∠1=75°,∠2=60°,∠3=75°,求∠4 的度数.
2.如图,已知∠1=60°,∠B=60°,∠C=40°,求∠DEC的度数.
典型案例探究
知识点 平行线的判定与性质的综合运用
【例题1】如图,已知C是BE上一点,∠1=∠E,∠B=∠D,试说明:AB∥CD.
【例题 2】如图,AB∥CD,AE,DF 分别是∠BAD,∠CDA 的平分线,AE 与DF 平行吗 为什么
【变式1】如图,已知∠1+∠2=180°,∠3=∠B.试说明:DE∥BC.
【变式2】如图,已知AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,AD平分∠BAC吗 若平分,请写出推理过程;若不平分,试说明理由.
课后作业
A 组
1.如图,已知AB∥DE,∠E=∠B.试说明:BC∥EF.
2.如图,若
试说明:
3.如图,已知∠A=∠1,∠C=∠F.试说明:BC∥EF.
4.如图,AB∥CD,∠B=115°,∠C=45°,求∠BEC的度数.
5.如图,已知点 P 在CD 上,∠BAP+∠APD=180°,∠1=∠2.试说明∠E=∠F.
B 组
6.如图,已知∠1+∠2=180°,∠A=∠C.
(1)试说明:AB∥CD;
(2)若AB平分∠DBE,试说明:CD平分∠BDF.
7.如图,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射后有∠1=∠2,∠3=∠4,请你解释为什么开始进入潜望镜的光线(AB)和最后离开潜望镜的光线(CD)是平行的.
C 组
8.已知:∠1=∠2,EG平分∠AEC.
(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°,试判断EF与CD的位置关系,并说明理由;
(2)如图②,当∠MAE,∠FEG,∠NCE之间满足什么关系时,AB∥CD
第3课时 命题、定理、证明
基础知识夯实
知识沉淀
1.命题:
(1)定义: 一件事情的语句,叫做命题.
(2)组成:命题由 和 两部分组成.题设是已知事项,结论是由已知事项推出的事项.
(3)改写:命题常可以写成“如果……那么……”的形式.
(4)分类:
① :如果题设成立,那么结论一定成立.
② :题设成立时,不能保证结论一定成立.
2.定理:命题的正确性是经过推理证实的,这样得到的 叫做定理.
定理可以作为继续推理的依据.
3.证明:在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做证明.
注意:判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
基础过关
1.判断下列语句是否是命题,若是,判断其真假.
(1)两直线平行,同位角相等. ( )
(2)对顶角相等. ( )
(3)内错角相等,两直线平行. ( )
(4)画一条线段. ( )
2.把下列命题改写成“如果……那么……”的形式.
(1)两直线平行,同旁内角互补.
答: ;
(2)对顶角相等.
答: ;
(3)内错角相等,两直线平行.
答: .
3.将下面推理过程,补充完整.
已知:如图,AB∥CD,∠A=∠C,
求证:∠E=∠F.
证明:∵AB∥CD(已知),∴∠C=∠ABF( ).
又∵∠A=∠C(已知),
∴∠A= ( ).
∴AE∥FC( ).
∴∠E=∠F( ).
典型案例探究
知识点1 命题的有关概念
【例题1】判断下列语句是不是命题 如果是命题,请判断其真假.
(1)两点之间,线段最短;
(2)请画出两条互相平行的直线;
(3)过直线外一点作已知直线的垂线;
(4)如果两个角的和是90°,那么这两个角互余.
(5)内错角相等.
【变式1】判断下列命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)若a∥b,b∥c,则a∥c;
(2)同位角相等,两直线平行;
(3)内错角相等;
(4)如果|a|=|b|,那么a=b;
(5)两个锐角互余.
知识点2 证明
【例题 2】 请 你 完 成 以 下推理.
已知:如图,BE∥CD,∠A=∠1.求证:∠C=∠E.
证明:∵BE∥CD(已知),∴∠2= ( ).又∵∠A=∠1(已知),
∴AC∥ ( ).
∴∠ =∠ ( ).
∴∠C=∠E(等量代换).
【变式2】请你完成以下推理.
如图,在梯形 ABCD中,AD∥BC,E 在BC 上,且∠A+∠1=180°.
求证:AB∥DE.
证明:∵AD∥BC( ),
∴∠ +∠B=180°( ).
又∵∠A+∠1=180°( ),
∴∠B=∠1( ).
∴ ∥ ( ).
课后作业
A 组
1.下列语句中,是命题的是 ( )
A.延长线段 AB B.垂线段最短
C.作直线l D.平行线与垂线
2.下列命题是假命题的是 ( )
A.直角的补角是直角 B.钝角的补角是锐角
C.垂线段最短 D.同旁内角互补
3.要判断命题“如果a>b,那么 是假命题,可举反例 ( )
A. a=1,b=-2 B. a=1,b=0
C. a=2,b=1 D. a=2,b=-1
4.下列说法中正确的是 ( )
A.命题是定理,定理是命题
B.命题不一定是定理,定理不一定是命题
C.真命题可以是定理,假命题不可能为定理
D.定理可能是真命题,也可能是假命题
5.把下列命题写成“如果……那么……”的形式:
(1)两直线相交,只有一个交点.
;
(2)邻补角互补.
··
6.写出下列命题的题设和结论:
(1)两直线平行,内错角相等.
题设是 ,结论是 ;
(2)垂直于同一直线的两直线平行.
题设是 ,结论是 .
7.把下面的推理过程补充完整,并在括号内填上理由.
已知:如图,B,C,E三点在一条直线上,∠3=∠E,∠4+∠2=180°.
求证:∠1=∠F.
证明:∵∠3=∠E(已知),∴EF∥ (内错角相等.两直线平行).
∵∠4+∠2=180°(已知),
∴CD∥AB( ).
∴CD∥ (平行于同一条直线的两条直线互相平行).
∴∠1=∠F( ).
B 组
8.如图,已知 AD⊥BC于点 D,FG⊥BC于点G,且∠1=∠2.求证:DE∥AC.
9.如图, ,求证:AE⊥EC.
C 组
10.如图,现有以下三句话:①AB∥CD;②∠B=∠C;③∠E=∠F.请以其中两句话为条件,第三句话为结论构造命题.
(1)你能构造哪儿个命题
(2)你构造的命题是真命题还是假命题 如果是真命题,请加以证明.
5.3 平行线的性质
第 1 课时平行线的性质
【基础知识夯实】
知识沉淀
相等相等 互补
a∥b ∠1=∠2 a∥b ∠1=∠2 a∥b
∠1+∠2=180°
基础过关
1. B2.60°60°120°
【典型案例探究】
例题1 C
变式1 C
例题2 B
变式 2 B
例题3解:∵AB∥CD.∴∠A+∠D=180°.
∵AD∥BC,∴∠C+∠D=180°.
∴∠A=∠C.
变式3解:∵AB∥CD,
∵EG平分∠BEF,
∴∠MEG=∠GEB+∠MEB=54°+72°=126°.
【课后作业】
1.74° 2.70° 3. D
4.∠2=110°,∠3=110°,∠4=70°
5.解:∵AE∥BC,
∴∠DAE=∠B,∠CAE=∠C.
∵∠B=∠C.
∴∠DAE=∠CAE,即 AE平分∠CAD.
6.解:如图, 处应按南偏西76°12'的方向开口.
7.15°
8.解:(1)过点 E向左作EF∥AB.
∴∠B+∠BEF=180°.
又∵AB∥CD,∴EF∥CD.
∴∠D+∠DEF=180°.
∴∠B+∠D+∠BEF+∠DEF=180°+180°=360°.
∴∠BEF+∠DEF=360°—∠B-∠D
即∠BED=78°.
(2)∠B+∠E+∠D=360°.
理由同(1)的求解过程.
9.解:(1)∠B=∠E.理由:
记 BC,EF的交点为O.
∵BA∥EF,BC∥DE,
∴∠B=∠EOC,∠EOC=∠E.
∴∠B=∠E.
(2)∠B+∠E=180°.理由:
记 BC,DE的交点为O.
∵BA∥ED,BC∥EF,
∴∠B=∠BOE,∠BOE+∠E=180°.
∴∠B+∠E=180°.
(3)如果两个角的两边分别平行,那么这两个角相等或互补.
第2课时 平行线的判定与性质的综合运用
【基础知识夯实】
知识沉淀
(1)相等相等
(2)相等 a∥b ∠1=∠2 相等 ∠1=∠2 a∥b
(3)互补 a∥b ∠1+∠2=180° 互补 ∠1+∠2=180° a∥b
基础过关
1.∠4=60° 2.∠DEC=140°
【典型案例探究】
例题1 解:∵∠1=∠E,∴AD∥BE.
∴∠2=∠D.
又∵∠B=∠D,∴∠2=∠B.∴AB∥CD.
变式1 解:∵∠1+∠2=180°,∠1+∠DFE=180°,
∴∠2=∠DFE.
∴AB∥EF.
∴∠3=∠ADE.
又∠3=∠B,
∴∠ADE=∠B.
∴DE∥BC.
例题2 解:AE∥DF.理由如下:
∵AB∥CD,∴∠BAD=∠CDA.
又∵AE是∠BAD的平分线,
DF 是∠CDA的平分线,
∴∠1=∠2.∴AE∥DF.
变式2解:AD平分∠BAC.理由如下:
∵AD⊥BC,EG⊥BC,∴AD∥EG.
∴∠1=∠E、∠2=∠3.
∵∠E=∠3,∴∠1=∠2,
即 AD平分∠BAC.
【课后作业】
1.解:∵AB∥DE,∴∠B=∠1.
又∵∠E=∠B,∴∠E=∠1.∴BC∥EF.
2.解:∵AB∥DE,∴∠1=∠2.
∵∠1+∠3=180°,∴∠2+∠3=180°.
∴BC∥EF.
3.解:∵∠A=∠1,∴AC∥DF.∴∠C=∠DGB.
又∵∠C=∠F,∴∠F=∠DGB.∴BC∥EF.
4.解:过点 E向左作EF∥AB,
∴∠BEF+∠B=180°.
又∵AB∥CD,∴EF∥CD.
∴∠CEF=∠C=45°.
∴
5.解:∵∠BAP+∠APD=180°,∴AB∥CD.
∴∠BAP=∠APC.
又∠1=∠2,∴∠BAP-∠1=∠APC-∠2,
即∠EAP=∠FPA.∴AE∥FP.∴∠E=∠F.
6.解:(1)∵∠1+∠DBE=180°,∠1+∠2=180°,
∴∠2=∠DBE.∴AD∥BC.∴∠A=∠ABE.
又∠A=∠C,
∴∠ABE=∠C.∴AB∥CD.
(2)∵AB平分∠DBE,∴∠ABE=∠ABD.
由(1)知AB∥CD,∴∠A=∠CDF,∠ABD=∠BDC.
由(1)知AD∥BC,∴∠ABE=∠A.
∴∠ABE=∠CDF.
∴∠BDC=∠CDF,即 CD平分∠BDF.
7.解:两个镜子是平行的,根据两直线平行,内错角相等得∠2=∠3.
又∵∠1=∠2,∠3=∠4,
即∠5=∠6.
根据内错角相等.两直线平行,可得AB∥CD,因此进入和离开潜望镜的光线是平行的.
8.解:(1)EF∥CD.理由如下:
∵∠1=∠2,∴AB∥EF.
∴∠AEF=∠MAE=45°.
∴∠AEG=∠AEF+∠FEG=45°+15°=60°.
∵EG平分∠AEC,∴∠CEG=∠AEG=60°.
∴∠CEF=∠CEG+∠FEG=75°.
又∠NCE=75°,∴∠NCE=∠CEF.
∴EF∥CD.
(2)当∠MAE=2∠FEG+∠NCE时,AB∥CD.理由如下:
∵∠1=∠2,∴AB∥EF.
要使AB∥CD,只需 CD∥EF,只需∠NCE+∠CEF=180°.
∵EG平分∠AEC,AB∥EF,
∴∠CEF=∠FEG+∠CEG=∠FEG+∠AEG=2∠FEG+∠AEF=2∠FEG+180°-∠MAE.
∴∠NCE+∠CEF=180°,即∠NCE+2∠FEG+180°-∠MAE=180°,即∠MAE=2∠FEG+∠NCE.
∴当∠MAE=2∠FEG+∠NCE时,AB∥CD.
第 3 课时 命题、定理、证明
【基础知识夯实】
知识沉淀
1.(1)判断 (2)题设 结论
(4)①真命题 ②假命题
2.真命题
基础过关
1.(1)真 (2)真 (3)真 (4)不是
2.(1)如果两直线平行,那么同旁内角互补
(2)如果两个角是对顶角,那么它们相等
(3)如果内错角相等,那么两直线平行
3.两直线平行,同位角相等 ∠ABF 等量代换
内错角相等,两直线平行 两直线平行,内错角相等
【典型案例探究】
例题1 (1)是命题,真命题
(2)不是命题
(3)不是命题
(4)是命题,真命题
(5)是命题,假命题
变式1 (1)真命题
(2)真命题
(3)假命题 反例略
(4)假命题 反例略
(5)假命题 反例略
例题2 ∠C 两直线平行,同位角相等 ED 内错角相等,两直线平行 2 E 两直线平行,内错角相等
变式2 已知 A 两直线平行,同旁内角互补 已知同角的补角相等 AB DE 同位角相等,两直线平行
【课后作业】
1. B 2. D 3. A 4. C
5.(1)如果两条直线相交,那么它们只有一个交点
(2)如果两个角是邻补角,那么它们互补
6.(1)两条平行直线被第三条直线所截 内错角相等
(2)两条直线垂直于同一条直线 这两条直线平行
7.AB 同旁内角互补,两直线平行 EF 两直线平行,内错角相等
8.证明:∵AD⊥BC,FG⊥BC,
∴AD∥FG.∴∠2=∠CAD.
又∠1=∠2,∴∠1=∠CAD.∴DE∥AC.
9.证明:过点 E向左作EF∥AB.
∵AB∥CD,∴EF∥CD.
∴∠CEF=∠ECD=60°.
∵EF∥AB,∴∠A=∠AEF=30°.
即 AE⊥EC.
10.解:(1)(j)如果AB∥CD,∠B=∠C,那么∠E=∠F.
(jì)如果AB∥CD,∠E=∠F,那么∠B=∠C.
(iii)如果∠B=∠C,∠E=∠F,那么AB∥CD.
(2)3个命题均为真命题.
(i) 证明:∵AB∥CD,∴∠B=∠CDF.
∵∠B=∠C,∴∠C=∠CDF.
∴CE∥BF.∴∠E=∠F.
(ii)证明:∵AB∥CD,∴∠B=∠CDF.
∵∠E=∠F.∴CE∥BF.∴∠C=∠CDF.
∴∠B=∠C.
(iii)证明:∵∠E=∠F,∴CE∥BF.∴∠C=∠CDF.
∵∠B=∠C.∴∠B=∠CDF.
∴AB∥CD.
第 1课时 平行线的性质
基础知识夯实
知识沉淀
平行线的性质:
平行线的性质 性质1 性质2 性质3
语言描述 两 直线 平 行,同位角______ 两 直 线 平 行,内错角______ 两直线平行,同旁内角_____
图例
几何语言 ________,
基础过关
1.下列四个图形中,已知直线a∥b,不能推出∠2 与∠1相等的是 ( )
中小学教育资源及组卷应用平台
2.如图,直线a,b被直线c 所截,且a∥b,∠1=60°,则∠2 = , ∠3 = ,∠4= .
典型案例探究
【例题 1】如图,直线a∥b,直线 c 与a,b相交,∠1=70°,则∠2 的大小是 ( )
A.20° B.50° C.80° D.100°
【变式1】如图,直线 a∥b,∠1=60°,∠2=40°,则∠3等于 ( )
A.40° B.60
C.70° D.110°
知识点 2 两直线平行,内错角相等
【例题2】如图,直线l ∥l ,直线 l 与 l ,l 分别交于点A,C,BC⊥l 交l 于点 B,若∠1=70°,则∠2 的度数为
A.10° B.20°
C.30° D.40°
【变 式 2】如图, 已 知 BE 平 分∠ABC,且 BE∥DC,若∠ABC=50°,则∠C的度数是 ( )
A.20° B.25°
C.30° D.50°
知识点 3 两直线平行,同旁内角互补
【例题3】如图,AB∥CD,AD∥BC,请说明∠A=∠C.
【变式3】如图,直线 AB∥CD,直线 MN 分别交AB,CD于点E,F,EG平分∠BEF,交 CD 于点 G,若∠EFG=72°,求∠MEG的度数.
课后作业
A 组
1.如图,用一吸管吮易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹角∠2= .
2.如图,直线 AB,CD 被直线AE所截,AB∥CD,∠A=110°,则∠1= .
3.如图,若AB∥CD,则下列结论一定成立的是( )
A.∠1=∠2 B. AD∥BC
C.∠B=∠D D.∠3=∠4
4.如图,已知直线a∥b,直线c∥d,∠1=110°,求∠2,∠3,∠4 的度数.
5.如图,∠B=∠C,AE∥BC.试说明:AE平分∠CAD.
6.如图,修高速公路需要开山洞,为节省时间,要在山两面A,B同时开工,在A 处测得洞的走向是北偏东76°12',那么在B处应按什么方向开口,才能使山洞准确接通 请说明其中的道理.
B 组
如图,将一副三角板和一张边线平行的纸条按如图所示方式摆放,两个三角板的一直角边重合,含 30°角的直角三角板的斜边与纸条一边重合,含 45°角的直角三角板的一个顶点在纸条的另一边上,则∠1的度数是 .
8.如图,已知
(1)若 求∠BED 的度数;
(2)请猜想 的度数,并说明理由.
C 组
9.如图①②,∠B,∠E的两边分别平行.
(1)在图①中,∠B 与∠E 有什么数量关系 为什么
(2)在图②中,∠B 与∠E 有什么数量关系 为什么
(3)由(1)(2)你能得出什么结论 用一句话概括你得到的结论.
第2课时 平行线的判定与性质的综合运用
基础知识夯实
知识沉淀
平行线的性质 图例 平行线的判定
(1)两直线平行,同位角_________, ∵a∥b, ∴∠1=∠2 ∵_________,两直线平行. ∵∠1=∠2,∴a∥b
(2)两直线平行,内错角________ ∵_______, ∴_______ 内错角_______,两直线平行. ∵_______, ∴_______
(3)两直线平行,同旁内角______ ∵_______, ∴__________ 同旁内角_______,两直线平行 同位角_______, ∴_______
基础过关
1.如图,∠1=75°,∠2=60°,∠3=75°,求∠4 的度数.
2.如图,已知∠1=60°,∠B=60°,∠C=40°,求∠DEC的度数.
典型案例探究
知识点 平行线的判定与性质的综合运用
【例题1】如图,已知C是BE上一点,∠1=∠E,∠B=∠D,试说明:AB∥CD.
【例题 2】如图,AB∥CD,AE,DF 分别是∠BAD,∠CDA 的平分线,AE 与DF 平行吗 为什么
【变式1】如图,已知∠1+∠2=180°,∠3=∠B.试说明:DE∥BC.
【变式2】如图,已知AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,AD平分∠BAC吗 若平分,请写出推理过程;若不平分,试说明理由.
课后作业
A 组
1.如图,已知AB∥DE,∠E=∠B.试说明:BC∥EF.
2.如图,若
试说明:
3.如图,已知∠A=∠1,∠C=∠F.试说明:BC∥EF.
4.如图,AB∥CD,∠B=115°,∠C=45°,求∠BEC的度数.
5.如图,已知点 P 在CD 上,∠BAP+∠APD=180°,∠1=∠2.试说明∠E=∠F.
B 组
6.如图,已知∠1+∠2=180°,∠A=∠C.
(1)试说明:AB∥CD;
(2)若AB平分∠DBE,试说明:CD平分∠BDF.
7.如图,潜望镜中的两个镜子是互相平行放置的,光线经过镜子反射后有∠1=∠2,∠3=∠4,请你解释为什么开始进入潜望镜的光线(AB)和最后离开潜望镜的光线(CD)是平行的.
C 组
8.已知:∠1=∠2,EG平分∠AEC.
(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°,试判断EF与CD的位置关系,并说明理由;
(2)如图②,当∠MAE,∠FEG,∠NCE之间满足什么关系时,AB∥CD
第3课时 命题、定理、证明
基础知识夯实
知识沉淀
1.命题:
(1)定义: 一件事情的语句,叫做命题.
(2)组成:命题由 和 两部分组成.题设是已知事项,结论是由已知事项推出的事项.
(3)改写:命题常可以写成“如果……那么……”的形式.
(4)分类:
① :如果题设成立,那么结论一定成立.
② :题设成立时,不能保证结论一定成立.
2.定理:命题的正确性是经过推理证实的,这样得到的 叫做定理.
定理可以作为继续推理的依据.
3.证明:在很多情况下,一个命题的正确性需要经过推理才能作出判断,这个推理过程叫做证明.
注意:判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
基础过关
1.判断下列语句是否是命题,若是,判断其真假.
(1)两直线平行,同位角相等. ( )
(2)对顶角相等. ( )
(3)内错角相等,两直线平行. ( )
(4)画一条线段. ( )
2.把下列命题改写成“如果……那么……”的形式.
(1)两直线平行,同旁内角互补.
答: ;
(2)对顶角相等.
答: ;
(3)内错角相等,两直线平行.
答: .
3.将下面推理过程,补充完整.
已知:如图,AB∥CD,∠A=∠C,
求证:∠E=∠F.
证明:∵AB∥CD(已知),∴∠C=∠ABF( ).
又∵∠A=∠C(已知),
∴∠A= ( ).
∴AE∥FC( ).
∴∠E=∠F( ).
典型案例探究
知识点1 命题的有关概念
【例题1】判断下列语句是不是命题 如果是命题,请判断其真假.
(1)两点之间,线段最短;
(2)请画出两条互相平行的直线;
(3)过直线外一点作已知直线的垂线;
(4)如果两个角的和是90°,那么这两个角互余.
(5)内错角相等.
【变式1】判断下列命题是真命题还是假命题,如果是假命题,举出一个反例.
(1)若a∥b,b∥c,则a∥c;
(2)同位角相等,两直线平行;
(3)内错角相等;
(4)如果|a|=|b|,那么a=b;
(5)两个锐角互余.
知识点2 证明
【例题 2】 请 你 完 成 以 下推理.
已知:如图,BE∥CD,∠A=∠1.求证:∠C=∠E.
证明:∵BE∥CD(已知),∴∠2= ( ).又∵∠A=∠1(已知),
∴AC∥ ( ).
∴∠ =∠ ( ).
∴∠C=∠E(等量代换).
【变式2】请你完成以下推理.
如图,在梯形 ABCD中,AD∥BC,E 在BC 上,且∠A+∠1=180°.
求证:AB∥DE.
证明:∵AD∥BC( ),
∴∠ +∠B=180°( ).
又∵∠A+∠1=180°( ),
∴∠B=∠1( ).
∴ ∥ ( ).
课后作业
A 组
1.下列语句中,是命题的是 ( )
A.延长线段 AB B.垂线段最短
C.作直线l D.平行线与垂线
2.下列命题是假命题的是 ( )
A.直角的补角是直角 B.钝角的补角是锐角
C.垂线段最短 D.同旁内角互补
3.要判断命题“如果a>b,那么 是假命题,可举反例 ( )
A. a=1,b=-2 B. a=1,b=0
C. a=2,b=1 D. a=2,b=-1
4.下列说法中正确的是 ( )
A.命题是定理,定理是命题
B.命题不一定是定理,定理不一定是命题
C.真命题可以是定理,假命题不可能为定理
D.定理可能是真命题,也可能是假命题
5.把下列命题写成“如果……那么……”的形式:
(1)两直线相交,只有一个交点.
;
(2)邻补角互补.
··
6.写出下列命题的题设和结论:
(1)两直线平行,内错角相等.
题设是 ,结论是 ;
(2)垂直于同一直线的两直线平行.
题设是 ,结论是 .
7.把下面的推理过程补充完整,并在括号内填上理由.
已知:如图,B,C,E三点在一条直线上,∠3=∠E,∠4+∠2=180°.
求证:∠1=∠F.
证明:∵∠3=∠E(已知),∴EF∥ (内错角相等.两直线平行).
∵∠4+∠2=180°(已知),
∴CD∥AB( ).
∴CD∥ (平行于同一条直线的两条直线互相平行).
∴∠1=∠F( ).
B 组
8.如图,已知 AD⊥BC于点 D,FG⊥BC于点G,且∠1=∠2.求证:DE∥AC.
9.如图, ,求证:AE⊥EC.
C 组
10.如图,现有以下三句话:①AB∥CD;②∠B=∠C;③∠E=∠F.请以其中两句话为条件,第三句话为结论构造命题.
(1)你能构造哪儿个命题
(2)你构造的命题是真命题还是假命题 如果是真命题,请加以证明.
5.3 平行线的性质
第 1 课时平行线的性质
【基础知识夯实】
知识沉淀
相等相等 互补
a∥b ∠1=∠2 a∥b ∠1=∠2 a∥b
∠1+∠2=180°
基础过关
1. B2.60°60°120°
【典型案例探究】
例题1 C
变式1 C
例题2 B
变式 2 B
例题3解:∵AB∥CD.∴∠A+∠D=180°.
∵AD∥BC,∴∠C+∠D=180°.
∴∠A=∠C.
变式3解:∵AB∥CD,
∵EG平分∠BEF,
∴∠MEG=∠GEB+∠MEB=54°+72°=126°.
【课后作业】
1.74° 2.70° 3. D
4.∠2=110°,∠3=110°,∠4=70°
5.解:∵AE∥BC,
∴∠DAE=∠B,∠CAE=∠C.
∵∠B=∠C.
∴∠DAE=∠CAE,即 AE平分∠CAD.
6.解:如图, 处应按南偏西76°12'的方向开口.
7.15°
8.解:(1)过点 E向左作EF∥AB.
∴∠B+∠BEF=180°.
又∵AB∥CD,∴EF∥CD.
∴∠D+∠DEF=180°.
∴∠B+∠D+∠BEF+∠DEF=180°+180°=360°.
∴∠BEF+∠DEF=360°—∠B-∠D
即∠BED=78°.
(2)∠B+∠E+∠D=360°.
理由同(1)的求解过程.
9.解:(1)∠B=∠E.理由:
记 BC,EF的交点为O.
∵BA∥EF,BC∥DE,
∴∠B=∠EOC,∠EOC=∠E.
∴∠B=∠E.
(2)∠B+∠E=180°.理由:
记 BC,DE的交点为O.
∵BA∥ED,BC∥EF,
∴∠B=∠BOE,∠BOE+∠E=180°.
∴∠B+∠E=180°.
(3)如果两个角的两边分别平行,那么这两个角相等或互补.
第2课时 平行线的判定与性质的综合运用
【基础知识夯实】
知识沉淀
(1)相等相等
(2)相等 a∥b ∠1=∠2 相等 ∠1=∠2 a∥b
(3)互补 a∥b ∠1+∠2=180° 互补 ∠1+∠2=180° a∥b
基础过关
1.∠4=60° 2.∠DEC=140°
【典型案例探究】
例题1 解:∵∠1=∠E,∴AD∥BE.
∴∠2=∠D.
又∵∠B=∠D,∴∠2=∠B.∴AB∥CD.
变式1 解:∵∠1+∠2=180°,∠1+∠DFE=180°,
∴∠2=∠DFE.
∴AB∥EF.
∴∠3=∠ADE.
又∠3=∠B,
∴∠ADE=∠B.
∴DE∥BC.
例题2 解:AE∥DF.理由如下:
∵AB∥CD,∴∠BAD=∠CDA.
又∵AE是∠BAD的平分线,
DF 是∠CDA的平分线,
∴∠1=∠2.∴AE∥DF.
变式2解:AD平分∠BAC.理由如下:
∵AD⊥BC,EG⊥BC,∴AD∥EG.
∴∠1=∠E、∠2=∠3.
∵∠E=∠3,∴∠1=∠2,
即 AD平分∠BAC.
【课后作业】
1.解:∵AB∥DE,∴∠B=∠1.
又∵∠E=∠B,∴∠E=∠1.∴BC∥EF.
2.解:∵AB∥DE,∴∠1=∠2.
∵∠1+∠3=180°,∴∠2+∠3=180°.
∴BC∥EF.
3.解:∵∠A=∠1,∴AC∥DF.∴∠C=∠DGB.
又∵∠C=∠F,∴∠F=∠DGB.∴BC∥EF.
4.解:过点 E向左作EF∥AB,
∴∠BEF+∠B=180°.
又∵AB∥CD,∴EF∥CD.
∴∠CEF=∠C=45°.
∴
5.解:∵∠BAP+∠APD=180°,∴AB∥CD.
∴∠BAP=∠APC.
又∠1=∠2,∴∠BAP-∠1=∠APC-∠2,
即∠EAP=∠FPA.∴AE∥FP.∴∠E=∠F.
6.解:(1)∵∠1+∠DBE=180°,∠1+∠2=180°,
∴∠2=∠DBE.∴AD∥BC.∴∠A=∠ABE.
又∠A=∠C,
∴∠ABE=∠C.∴AB∥CD.
(2)∵AB平分∠DBE,∴∠ABE=∠ABD.
由(1)知AB∥CD,∴∠A=∠CDF,∠ABD=∠BDC.
由(1)知AD∥BC,∴∠ABE=∠A.
∴∠ABE=∠CDF.
∴∠BDC=∠CDF,即 CD平分∠BDF.
7.解:两个镜子是平行的,根据两直线平行,内错角相等得∠2=∠3.
又∵∠1=∠2,∠3=∠4,
即∠5=∠6.
根据内错角相等.两直线平行,可得AB∥CD,因此进入和离开潜望镜的光线是平行的.
8.解:(1)EF∥CD.理由如下:
∵∠1=∠2,∴AB∥EF.
∴∠AEF=∠MAE=45°.
∴∠AEG=∠AEF+∠FEG=45°+15°=60°.
∵EG平分∠AEC,∴∠CEG=∠AEG=60°.
∴∠CEF=∠CEG+∠FEG=75°.
又∠NCE=75°,∴∠NCE=∠CEF.
∴EF∥CD.
(2)当∠MAE=2∠FEG+∠NCE时,AB∥CD.理由如下:
∵∠1=∠2,∴AB∥EF.
要使AB∥CD,只需 CD∥EF,只需∠NCE+∠CEF=180°.
∵EG平分∠AEC,AB∥EF,
∴∠CEF=∠FEG+∠CEG=∠FEG+∠AEG=2∠FEG+∠AEF=2∠FEG+180°-∠MAE.
∴∠NCE+∠CEF=180°,即∠NCE+2∠FEG+180°-∠MAE=180°,即∠MAE=2∠FEG+∠NCE.
∴当∠MAE=2∠FEG+∠NCE时,AB∥CD.
第 3 课时 命题、定理、证明
【基础知识夯实】
知识沉淀
1.(1)判断 (2)题设 结论
(4)①真命题 ②假命题
2.真命题
基础过关
1.(1)真 (2)真 (3)真 (4)不是
2.(1)如果两直线平行,那么同旁内角互补
(2)如果两个角是对顶角,那么它们相等
(3)如果内错角相等,那么两直线平行
3.两直线平行,同位角相等 ∠ABF 等量代换
内错角相等,两直线平行 两直线平行,内错角相等
【典型案例探究】
例题1 (1)是命题,真命题
(2)不是命题
(3)不是命题
(4)是命题,真命题
(5)是命题,假命题
变式1 (1)真命题
(2)真命题
(3)假命题 反例略
(4)假命题 反例略
(5)假命题 反例略
例题2 ∠C 两直线平行,同位角相等 ED 内错角相等,两直线平行 2 E 两直线平行,内错角相等
变式2 已知 A 两直线平行,同旁内角互补 已知同角的补角相等 AB DE 同位角相等,两直线平行
【课后作业】
1. B 2. D 3. A 4. C
5.(1)如果两条直线相交,那么它们只有一个交点
(2)如果两个角是邻补角,那么它们互补
6.(1)两条平行直线被第三条直线所截 内错角相等
(2)两条直线垂直于同一条直线 这两条直线平行
7.AB 同旁内角互补,两直线平行 EF 两直线平行,内错角相等
8.证明:∵AD⊥BC,FG⊥BC,
∴AD∥FG.∴∠2=∠CAD.
又∠1=∠2,∴∠1=∠CAD.∴DE∥AC.
9.证明:过点 E向左作EF∥AB.
∵AB∥CD,∴EF∥CD.
∴∠CEF=∠ECD=60°.
∵EF∥AB,∴∠A=∠AEF=30°.
即 AE⊥EC.
10.解:(1)(j)如果AB∥CD,∠B=∠C,那么∠E=∠F.
(jì)如果AB∥CD,∠E=∠F,那么∠B=∠C.
(iii)如果∠B=∠C,∠E=∠F,那么AB∥CD.
(2)3个命题均为真命题.
(i) 证明:∵AB∥CD,∴∠B=∠CDF.
∵∠B=∠C,∴∠C=∠CDF.
∴CE∥BF.∴∠E=∠F.
(ii)证明:∵AB∥CD,∴∠B=∠CDF.
∵∠E=∠F.∴CE∥BF.∴∠C=∠CDF.
∴∠B=∠C.
(iii)证明:∵∠E=∠F,∴CE∥BF.∴∠C=∠CDF.
∵∠B=∠C.∴∠B=∠CDF.
∴AB∥CD.
