5.2 平行线及其判定同步课时练习(含答案)
文档属性
| 名称 | 5.2 平行线及其判定同步课时练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 653.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 09:51:13 | ||
图片预览


文档简介
5.2 平行线及其判定同步课时练习
第1课时 平行线
基础知识夯实
知识沉淀
1.平行线:
(1)定义:在同一平面内,不相交的两条直线叫做
(2)位置关系:在同一平面内,不重合的两条直线的位置关系有: 和 .
2.平行公理及其推论:
(1)平行公理:经过直线外一点,有且只有 直线与这条直线平行.
(2)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相 ,即如果b∥a,c∥a,那么b∥c.
基础过关
1.在同一平面内,直线 l 与 l 满足下列条件,写出其对应的位置关系.
(1)l 与l 没有公共点,则l 与l ;
(2) l 与 l 有 且 只 有 一 个 公 共 点, 则 l 与l ;
(3)l 与l 有两个公共点,则l 与 l .
2.下列语句中正确的有 ( )
①任意两条直线的位置关系不是相交就是平行;
②过一点有且只有一条直线和已知直线平行;
③过两条直线a,b外一点P,画直线c,使c∥a,且c//b;
④若直线a∥b,b∥c,则c∥a.
A.4 个 B.3 个 C.2 个 D.1 个
典型案例探究
知识点 1 平行线的概念
【例题1】判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
知识点 2 平行线的画法
【例题2】读下列语句,并画出图形.
(1)如图(1),过点 A画EF∥BC;
(2)如图(2),在∠AOB 内取一点 P,过点 P 画PC∥OA交OB 于点C,PD∥OB交OA 于点D.
知识点3 平行公理及其推论
【例题3】如图,已知OA∥CD,OB∥CD,那么∠AOB是平角吗 为什么
课后作业
A 组
1.下列实例:①门框的左右两边;②楼梯的两个台阶;③水桶的上口边缘;④直立于地面的两根电线杆.其中给我们以平行线形象的有 ( )
A.1个 B.2 个 C.3个 D.4个
2.下列说法:
①过一点有且只有一条直线与已知直线平行;
②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条直线平行.
其中正确的有 ( )
A.3个 B.2个 C.1个 D.0个
3.下面说法中正确的是 ( )
A.在同一平面内,两条直线的位置关系有相交、平行、垂直三种
B.在同一平面内,不垂直的两条直线必平行
C.在同一平面内,不平行的两条直线必垂直
D.在同一平面内,不相交的两条直线一定不垂直
4.下列推理正确的是 ( )
A.因为a∥b,c∥d,所以b∥d
B.因为a∥c,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c
D.因为a∥b,c∥d,所以a∥c
5.若点 P 为直线AB 外一点,则过点 P 且平行于 AB的直线有 条.
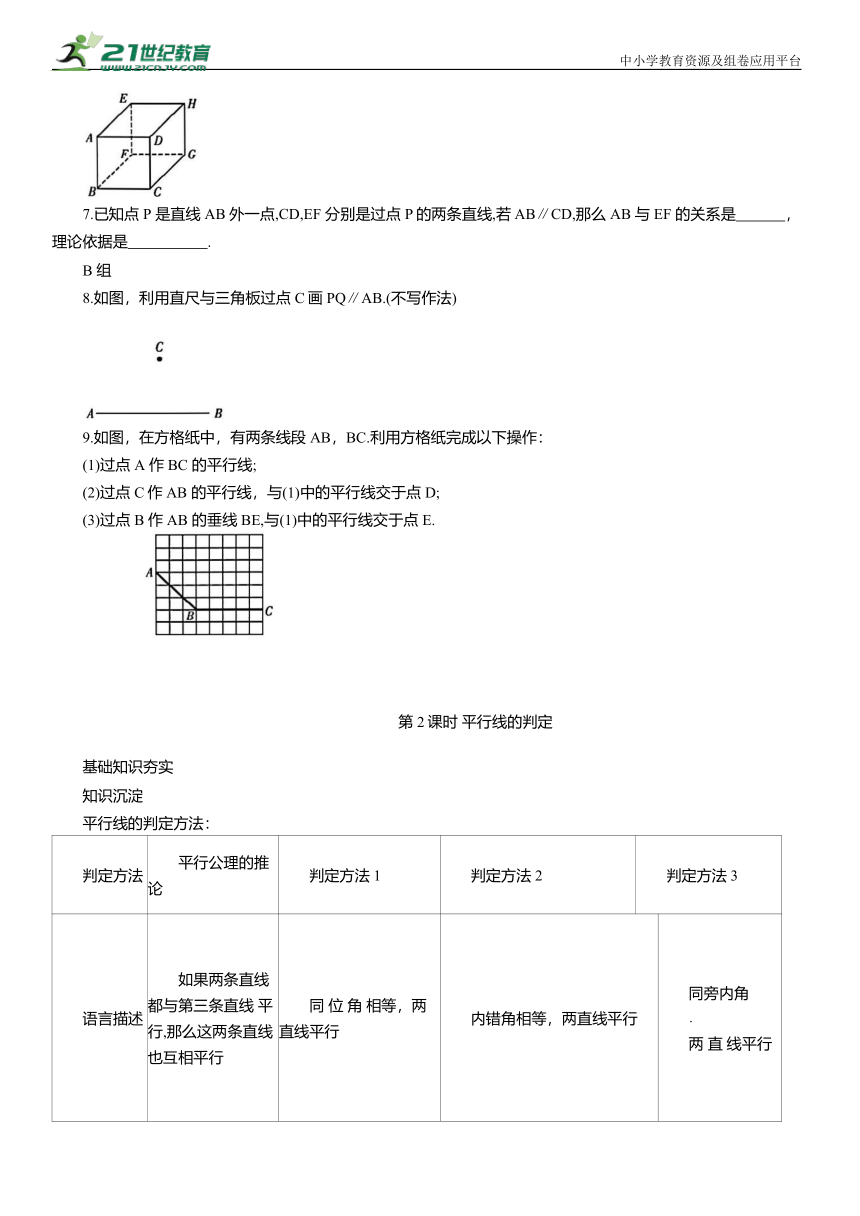
6.如图,在正方体中,与线段AB平行的线段有
7.已知点 P 是直线AB 外一点,CD,EF 分别是过点 P的两条直线,若AB∥CD,那么 AB 与EF 的关系是 ,理论依据是 .
B 组
8.如图,利用直尺与三角板过点C画PQ∥AB.(不写作法)
9.如图,在方格纸中,有两条线段AB,BC.利用方格纸完成以下操作:
(1)过点 A 作BC 的平行线;
(2)过点 C作AB 的平行线,与(1)中的平行线交于点 D;
(3)过点 B 作AB 的垂线BE,与(1)中的平行线交于点 E.
平行线的判定
基础知识夯实
中小学教育资源及组卷应用平台
知识沉淀
平行线的判定方法:
判定方法 平行公理的推论 判定方法1 判定方法2 判定方法3
语言描述 如果两条直线都与第三条直线 平 行,那么这两条直线也互相平行 同 位 角 相等,两直线平行 内错角相等,两直线平行 同旁内角 · 两 直 线平行
图例
几何语言 ∵_____, ∴b∥c ∵______. ∴a∥b ∵________,∴a∥b ∵_____, ∴a∥b
基础过关
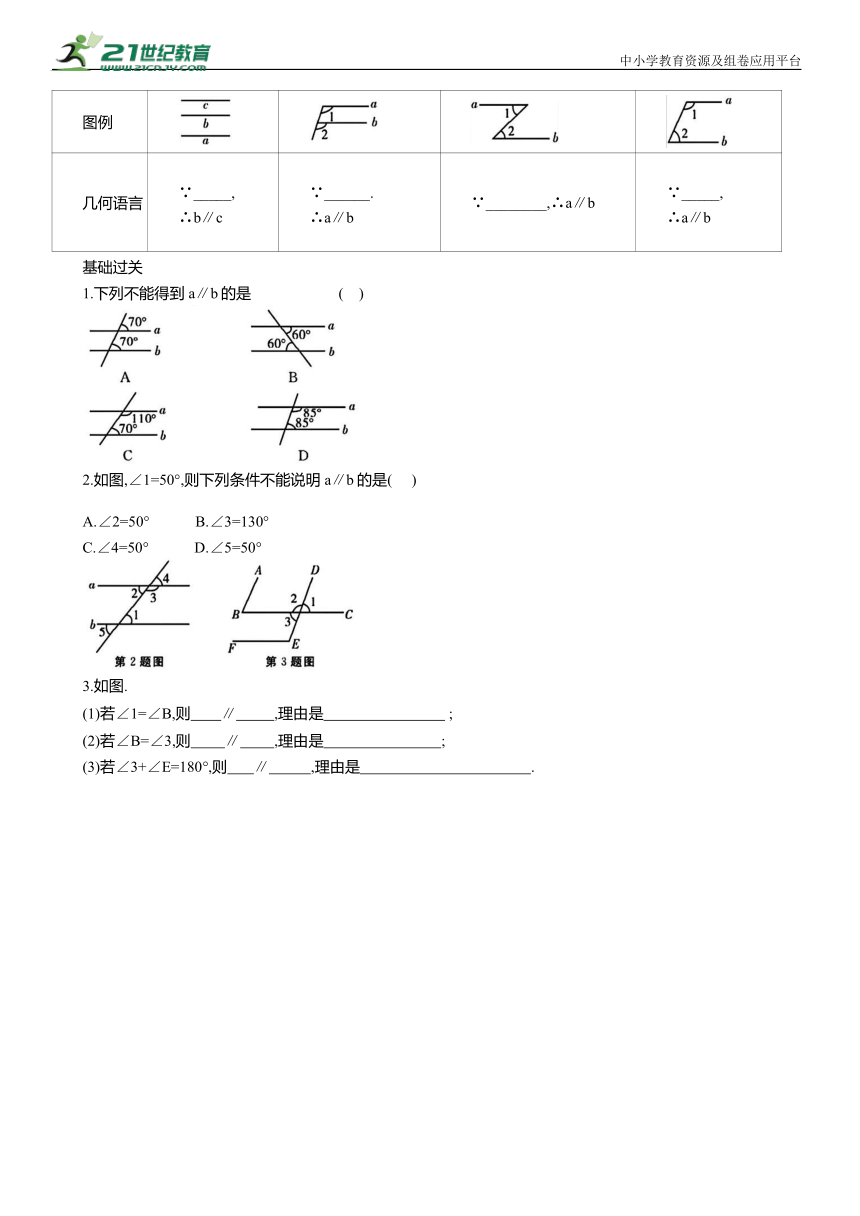
1.下列不能得到a∥b的是 ( )
2.如图,∠1=50°,则下列条件不能说明a∥b的是( )
A.∠2=50° B.∠3=130°
C.∠4=50° D.∠5=50°
3.如图.
(1)若∠1=∠B,则 ∥ ,理由是 ;
(2)若∠B=∠3,则 ∥ ,理由是 ;
(3)若∠3+∠E=180°,则 ∥ ,理由是 .
典型案例探究
知识点 1 同位角相等,两直线平行
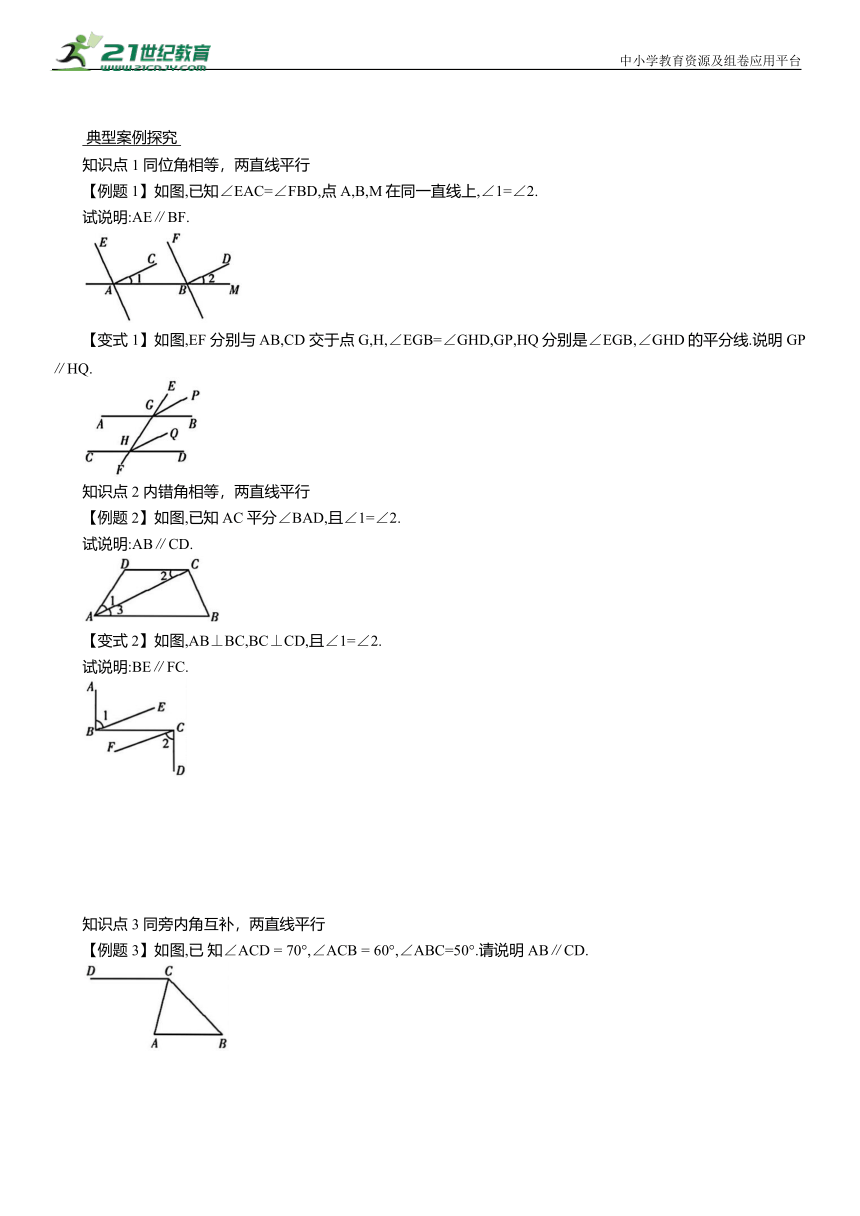
【例题1】如图,已知∠EAC=∠FBD,点A,B,M在同一直线上,∠1=∠2.
试说明:AE∥BF.
【变式 1】如图,EF 分别与AB,CD 交于点 G,H,∠EGB=∠GHD,GP,HQ分别是∠EGB,∠GHD的平分线.说明GP∥HQ.
知识点 2 内错角相等,两直线平行
【例题2】如图,已知AC平分∠BAD,且∠1=∠2.
试说明:AB∥CD.
【变式2】如图,AB⊥BC,BC⊥CD,且∠1=∠2.
试说明:BE∥FC.
知识点 3 同旁内角互补,两直线平行
【例题 3】如图,已 知∠ACD = 70°,∠ACB = 60°,∠ABC=50°.请说明AB∥CD.
【变式3】如图,AB⊥BD 于点 B,CD⊥BD 于点 D,∠1+∠2=180°,试问 CD与EF 平行吗 为什么
课后作业
A 组
1.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是 ( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
2.如图, 如果∠D=∠EFC,那么 ( )
A. AD∥BC B. EF∥BC
C. AB∥DC D. AD∥EF
3.如图,点 E 在AC 的延长线上,下列条件中能判断AB∥CD的是 ( )
A.∠3=∠4 B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
4.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度可能是
( )
A.第一次右拐50°,第二次左拐130°
B.第一次左拐50°,第二次右拐130°
C.第一次左拐50°,第二次左拐130°
D.第一次右拐50°,第二次左拐50°
5.在同一平面内,如果直线b和c 都与直线a 垂直,那么直线b和c 的位置关系是 .
6.如图,小明利用两块相同的三角板,分别在三角板的边缘画直线 AB 和CD,可得 AB∥CD,这是根据 ,两直线平行.
7.如图,直线a,b与直线c相交,给出下列条件:
①∠1=∠2;
②∠4=∠6;
③∠4+∠7=180°;
④∠5+∠3=180°.
其中能判断a∥b的条件是 (只填序号).
B 组
8.如图,已知∠1=70°,∠2=110°,请用三种方法判定AB∥DE.
9.如图,已知 ,BA,EF 相交于点M, ,试判断 BC 与 EF 是否平行,并说明理由.
C 组
10.(1)如图1,∠ABE=∠CDE+∠BED,∠DEF=∠CDE,AB与EF平行吗 说明理由.
(2)如图2,点E是直线AB,CD外一点,∠ABE=∠CDE+∠BED,AB与CD平行吗 说明理由.
【基础知识夯实】
知识沉淀
1.(1)平行线 (2)相交 平行
2.(1)一条 (2)平行
基础过关
1.(1)平行 (2)相交 (3)重合 2. D
【典型案例探究】
例题1 解:(1)不正确.理由:缺少了“在同一平面内”这一条件.
(2)不正确.理由:两条线段所在的直线不相交,才是平行线.
变式1 ①②③
例题2 (1)E
变式2
例题3 解:∠AOB是平角.
因为OA∥CD,OB∥CD且OA,OB交于点O,根据过直线CD外一点O 有且只有一条直线与已知直线CD平行,
所以OA,OB共直线.
所以点 A,O,B共直线,即∠AOB是平角.
变式3 解:a∥d.理由如下:
因为a∥b,b∥c,所以a∥c.
因为a∥c,c∥d,所以a∥d.
【课后作业】
1. C2. C 3. D 4. C 5.1
6. EF,HG,DC
7.相交 经过直线外一点,有且只有一条直线与这条直线平行
平行线的判定
【基础知识夯实】
知识沉淀
互补
b∥a,c∥a ∠1=∠2 ∠1=∠2 ∠1+∠2=180°
基础过关
1. D 2. D
3.(1)ABDE同位角相等,两直线平行
(2)AB DE 内错角相等,两直线平行
(3)BC EF 同旁内角互补,两直线平行
【典型案例探究】
例题1 解:∵∠EAC=∠FBD,∠1=∠2,∴∠EAC+∠1=∠FBD+∠2,即∠EAB=∠FBM.
∴AE∥BF(同位角相等,两直线平行).
变式1 解:∵∠EGB=∠GHD,
∵GP 平分∠EGB,HQ平分∠GHD,
∴∠EGP=∠EHQ.∴GP∥HQ(同位角相等,两直线平行).
例题2 解:∵AC平分∠BAD,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=3.
∴AB∥CD(内错角相等,两直线平行).
变式2 解:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠BCD=90°.
又∵∠1=∠2,∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.∴BE∥FC(内错角相等,两直线平行).
例题3 解:∵∠ACD=70°,∠ACB=60°,
∴∠BCD=∠ACB+∠ACD=130°.
∵∠ABC=50°,∴∠ABC+∠BCD=180°.
∴AB∥CD(同旁内角互补,两直线平行).
变式3 解:CD∥EF. 理由如下:
∵AB⊥BD,CD⊥BD.
∴∠ABD=∠CDB=90°.
∴∠ABD+∠CDB=180°.
∴AB∥CD(同旁内角互补,两直线平行).
∵∠1+∠2=180°,
∴AB∥EF(同旁内角互补,两直线平行).
∴CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
【课后作业】
1. A 2. D 3. B 4. D 5.平行
6.内错角相等 7.①③④
8.解:如图,
方法一:因为∠1=70°,所以 .因为∠2=110°,所以∠2=∠4.
所以AB∥DE(同位角相等.两直线平行).
方法二:因为∠1=70°,所以. 因为∠2=110°,所以∠2=∠5.所以AB∥DE(内错角相等,两直线平行).
方法三:因为∠1=70°,所以∠3=70°.因为∠2=110°,所以∠2+∠3=180°.所以AB∥DE(同旁内角互补,两直线平行).
9.解:BC∥EF,理由如下:
∵∠DEF+∠AME=180°(已知),∠AME+∠AMF=180°.
∴∠AMF=∠DEF.
∵∠ABC=∠DEF(已知),
∴∠AMF=∠ABC(等量代换).
∴BC∥EF(同位角相等,两直线平行).
10.解:(1) AB∥EF.理由如下:
∵∠ABE=∠CDE+∠BED,∠DEF=∠CDE,
∴∠ABE=∠DEF+∠BED,即∠ABE=∠BEF.
∴AB∥EF.
(2)AB∥CD.理由如下:过点 E 作射线EF,使得∠DEF=∠CDE,
∴CD∥EF.
∵∠ABE=∠CDE+∠BED,∠DEF=∠CDE,
∴∠ABE=∠DEF+∠BED,即∠ABE=∠BEF.
∴AB∥EF.
∴AB∥CD.
第1课时 平行线
基础知识夯实
知识沉淀
1.平行线:
(1)定义:在同一平面内,不相交的两条直线叫做
(2)位置关系:在同一平面内,不重合的两条直线的位置关系有: 和 .
2.平行公理及其推论:
(1)平行公理:经过直线外一点,有且只有 直线与这条直线平行.
(2)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相 ,即如果b∥a,c∥a,那么b∥c.
基础过关
1.在同一平面内,直线 l 与 l 满足下列条件,写出其对应的位置关系.
(1)l 与l 没有公共点,则l 与l ;
(2) l 与 l 有 且 只 有 一 个 公 共 点, 则 l 与l ;
(3)l 与l 有两个公共点,则l 与 l .
2.下列语句中正确的有 ( )
①任意两条直线的位置关系不是相交就是平行;
②过一点有且只有一条直线和已知直线平行;
③过两条直线a,b外一点P,画直线c,使c∥a,且c//b;
④若直线a∥b,b∥c,则c∥a.
A.4 个 B.3 个 C.2 个 D.1 个
典型案例探究
知识点 1 平行线的概念
【例题1】判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
知识点 2 平行线的画法
【例题2】读下列语句,并画出图形.
(1)如图(1),过点 A画EF∥BC;
(2)如图(2),在∠AOB 内取一点 P,过点 P 画PC∥OA交OB 于点C,PD∥OB交OA 于点D.
知识点3 平行公理及其推论
【例题3】如图,已知OA∥CD,OB∥CD,那么∠AOB是平角吗 为什么
课后作业
A 组
1.下列实例:①门框的左右两边;②楼梯的两个台阶;③水桶的上口边缘;④直立于地面的两根电线杆.其中给我们以平行线形象的有 ( )
A.1个 B.2 个 C.3个 D.4个
2.下列说法:
①过一点有且只有一条直线与已知直线平行;
②一条直线的平行线只有一条;
③过直线外一点,有且只有一条直线与这条直线平行.
其中正确的有 ( )
A.3个 B.2个 C.1个 D.0个
3.下面说法中正确的是 ( )
A.在同一平面内,两条直线的位置关系有相交、平行、垂直三种
B.在同一平面内,不垂直的两条直线必平行
C.在同一平面内,不平行的两条直线必垂直
D.在同一平面内,不相交的两条直线一定不垂直
4.下列推理正确的是 ( )
A.因为a∥b,c∥d,所以b∥d
B.因为a∥c,b∥d,所以c∥d
C.因为a∥b,a∥c,所以b∥c
D.因为a∥b,c∥d,所以a∥c
5.若点 P 为直线AB 外一点,则过点 P 且平行于 AB的直线有 条.
6.如图,在正方体中,与线段AB平行的线段有
7.已知点 P 是直线AB 外一点,CD,EF 分别是过点 P的两条直线,若AB∥CD,那么 AB 与EF 的关系是 ,理论依据是 .
B 组
8.如图,利用直尺与三角板过点C画PQ∥AB.(不写作法)
9.如图,在方格纸中,有两条线段AB,BC.利用方格纸完成以下操作:
(1)过点 A 作BC 的平行线;
(2)过点 C作AB 的平行线,与(1)中的平行线交于点 D;
(3)过点 B 作AB 的垂线BE,与(1)中的平行线交于点 E.
平行线的判定
基础知识夯实
中小学教育资源及组卷应用平台
知识沉淀
平行线的判定方法:
判定方法 平行公理的推论 判定方法1 判定方法2 判定方法3
语言描述 如果两条直线都与第三条直线 平 行,那么这两条直线也互相平行 同 位 角 相等,两直线平行 内错角相等,两直线平行 同旁内角 · 两 直 线平行
图例
几何语言 ∵_____, ∴b∥c ∵______. ∴a∥b ∵________,∴a∥b ∵_____, ∴a∥b
基础过关
1.下列不能得到a∥b的是 ( )
2.如图,∠1=50°,则下列条件不能说明a∥b的是( )
A.∠2=50° B.∠3=130°
C.∠4=50° D.∠5=50°
3.如图.
(1)若∠1=∠B,则 ∥ ,理由是 ;
(2)若∠B=∠3,则 ∥ ,理由是 ;
(3)若∠3+∠E=180°,则 ∥ ,理由是 .
典型案例探究
知识点 1 同位角相等,两直线平行
【例题1】如图,已知∠EAC=∠FBD,点A,B,M在同一直线上,∠1=∠2.
试说明:AE∥BF.
【变式 1】如图,EF 分别与AB,CD 交于点 G,H,∠EGB=∠GHD,GP,HQ分别是∠EGB,∠GHD的平分线.说明GP∥HQ.
知识点 2 内错角相等,两直线平行
【例题2】如图,已知AC平分∠BAD,且∠1=∠2.
试说明:AB∥CD.
【变式2】如图,AB⊥BC,BC⊥CD,且∠1=∠2.
试说明:BE∥FC.
知识点 3 同旁内角互补,两直线平行
【例题 3】如图,已 知∠ACD = 70°,∠ACB = 60°,∠ABC=50°.请说明AB∥CD.
【变式3】如图,AB⊥BD 于点 B,CD⊥BD 于点 D,∠1+∠2=180°,试问 CD与EF 平行吗 为什么
课后作业
A 组
1.如图,是我们学过的用直尺和三角尺画平行线的方法示意图,画图的原理是 ( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.两直线平行,同位角相等
D.两直线平行,内错角相等
2.如图, 如果∠D=∠EFC,那么 ( )
A. AD∥BC B. EF∥BC
C. AB∥DC D. AD∥EF
3.如图,点 E 在AC 的延长线上,下列条件中能判断AB∥CD的是 ( )
A.∠3=∠4 B.∠1=∠2
C.∠D=∠DCE D.∠D+∠ACD=180°
4.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度可能是
( )
A.第一次右拐50°,第二次左拐130°
B.第一次左拐50°,第二次右拐130°
C.第一次左拐50°,第二次左拐130°
D.第一次右拐50°,第二次左拐50°
5.在同一平面内,如果直线b和c 都与直线a 垂直,那么直线b和c 的位置关系是 .
6.如图,小明利用两块相同的三角板,分别在三角板的边缘画直线 AB 和CD,可得 AB∥CD,这是根据 ,两直线平行.
7.如图,直线a,b与直线c相交,给出下列条件:
①∠1=∠2;
②∠4=∠6;
③∠4+∠7=180°;
④∠5+∠3=180°.
其中能判断a∥b的条件是 (只填序号).
B 组
8.如图,已知∠1=70°,∠2=110°,请用三种方法判定AB∥DE.
9.如图,已知 ,BA,EF 相交于点M, ,试判断 BC 与 EF 是否平行,并说明理由.
C 组
10.(1)如图1,∠ABE=∠CDE+∠BED,∠DEF=∠CDE,AB与EF平行吗 说明理由.
(2)如图2,点E是直线AB,CD外一点,∠ABE=∠CDE+∠BED,AB与CD平行吗 说明理由.
【基础知识夯实】
知识沉淀
1.(1)平行线 (2)相交 平行
2.(1)一条 (2)平行
基础过关
1.(1)平行 (2)相交 (3)重合 2. D
【典型案例探究】
例题1 解:(1)不正确.理由:缺少了“在同一平面内”这一条件.
(2)不正确.理由:两条线段所在的直线不相交,才是平行线.
变式1 ①②③
例题2 (1)E
变式2
例题3 解:∠AOB是平角.
因为OA∥CD,OB∥CD且OA,OB交于点O,根据过直线CD外一点O 有且只有一条直线与已知直线CD平行,
所以OA,OB共直线.
所以点 A,O,B共直线,即∠AOB是平角.
变式3 解:a∥d.理由如下:
因为a∥b,b∥c,所以a∥c.
因为a∥c,c∥d,所以a∥d.
【课后作业】
1. C2. C 3. D 4. C 5.1
6. EF,HG,DC
7.相交 经过直线外一点,有且只有一条直线与这条直线平行
平行线的判定
【基础知识夯实】
知识沉淀
互补
b∥a,c∥a ∠1=∠2 ∠1=∠2 ∠1+∠2=180°
基础过关
1. D 2. D
3.(1)ABDE同位角相等,两直线平行
(2)AB DE 内错角相等,两直线平行
(3)BC EF 同旁内角互补,两直线平行
【典型案例探究】
例题1 解:∵∠EAC=∠FBD,∠1=∠2,∴∠EAC+∠1=∠FBD+∠2,即∠EAB=∠FBM.
∴AE∥BF(同位角相等,两直线平行).
变式1 解:∵∠EGB=∠GHD,
∵GP 平分∠EGB,HQ平分∠GHD,
∴∠EGP=∠EHQ.∴GP∥HQ(同位角相等,两直线平行).
例题2 解:∵AC平分∠BAD,
∴∠1=∠3.
又∵∠1=∠2,
∴∠2=3.
∴AB∥CD(内错角相等,两直线平行).
变式2 解:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠BCD=90°.
又∵∠1=∠2,∴∠ABC-∠1=∠BCD-∠2,即∠EBC=∠BCF.∴BE∥FC(内错角相等,两直线平行).
例题3 解:∵∠ACD=70°,∠ACB=60°,
∴∠BCD=∠ACB+∠ACD=130°.
∵∠ABC=50°,∴∠ABC+∠BCD=180°.
∴AB∥CD(同旁内角互补,两直线平行).
变式3 解:CD∥EF. 理由如下:
∵AB⊥BD,CD⊥BD.
∴∠ABD=∠CDB=90°.
∴∠ABD+∠CDB=180°.
∴AB∥CD(同旁内角互补,两直线平行).
∵∠1+∠2=180°,
∴AB∥EF(同旁内角互补,两直线平行).
∴CD∥EF(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).
【课后作业】
1. A 2. D 3. B 4. D 5.平行
6.内错角相等 7.①③④
8.解:如图,
方法一:因为∠1=70°,所以 .因为∠2=110°,所以∠2=∠4.
所以AB∥DE(同位角相等.两直线平行).
方法二:因为∠1=70°,所以. 因为∠2=110°,所以∠2=∠5.所以AB∥DE(内错角相等,两直线平行).
方法三:因为∠1=70°,所以∠3=70°.因为∠2=110°,所以∠2+∠3=180°.所以AB∥DE(同旁内角互补,两直线平行).
9.解:BC∥EF,理由如下:
∵∠DEF+∠AME=180°(已知),∠AME+∠AMF=180°.
∴∠AMF=∠DEF.
∵∠ABC=∠DEF(已知),
∴∠AMF=∠ABC(等量代换).
∴BC∥EF(同位角相等,两直线平行).
10.解:(1) AB∥EF.理由如下:
∵∠ABE=∠CDE+∠BED,∠DEF=∠CDE,
∴∠ABE=∠DEF+∠BED,即∠ABE=∠BEF.
∴AB∥EF.
(2)AB∥CD.理由如下:过点 E 作射线EF,使得∠DEF=∠CDE,
∴CD∥EF.
∵∠ABE=∠CDE+∠BED,∠DEF=∠CDE,
∴∠ABE=∠DEF+∠BED,即∠ABE=∠BEF.
∴AB∥EF.
∴AB∥CD.
