5.1相交线同步课时练习(含答案)
图片预览



文档简介
第五章 相交线与平行线
5.1相交线同步课时练习
第 1课时 相交线
基础知识夯实
知识沉淀
1.邻补角:
(1)概念:如图,∠1 和∠2 有一条公共边 OC,它们的另一边互为反向延长线(∠1 和∠2 互补),具有这种关系的两个角,互为 .图中还有其他的邻补角: .
(2)性质:邻补角 .
2.对顶角:
(1)概念:如图,∠1和∠3 有一个公共顶点 O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为 .图中还有其他的对顶角: .
(2)性质:对顶角 .
基础过关
1.下列各图中,∠1 和∠2 是邻补角吗 为什么
2.下列各图中,∠1 和∠2 是对顶角吗 为什么
典型案例探究
知识点1 邻补角、对顶角的定义
【例题1】如图,直线 AB,CD 交于点O,OE 为以点O为端点的射线,写出图中所有的邻补角和对顶角.
【变式1】如图,三条直线 AB ,CD ,EF 相交于点O,∠AOE 的对顶角是 ,∠EOD 的邻补角是 .
知识点 2 邻补角、对顶角的性质
【例题2】如图,直线a,b相交于点O,∠1=30°,求∠2,∠3,∠4的度数.
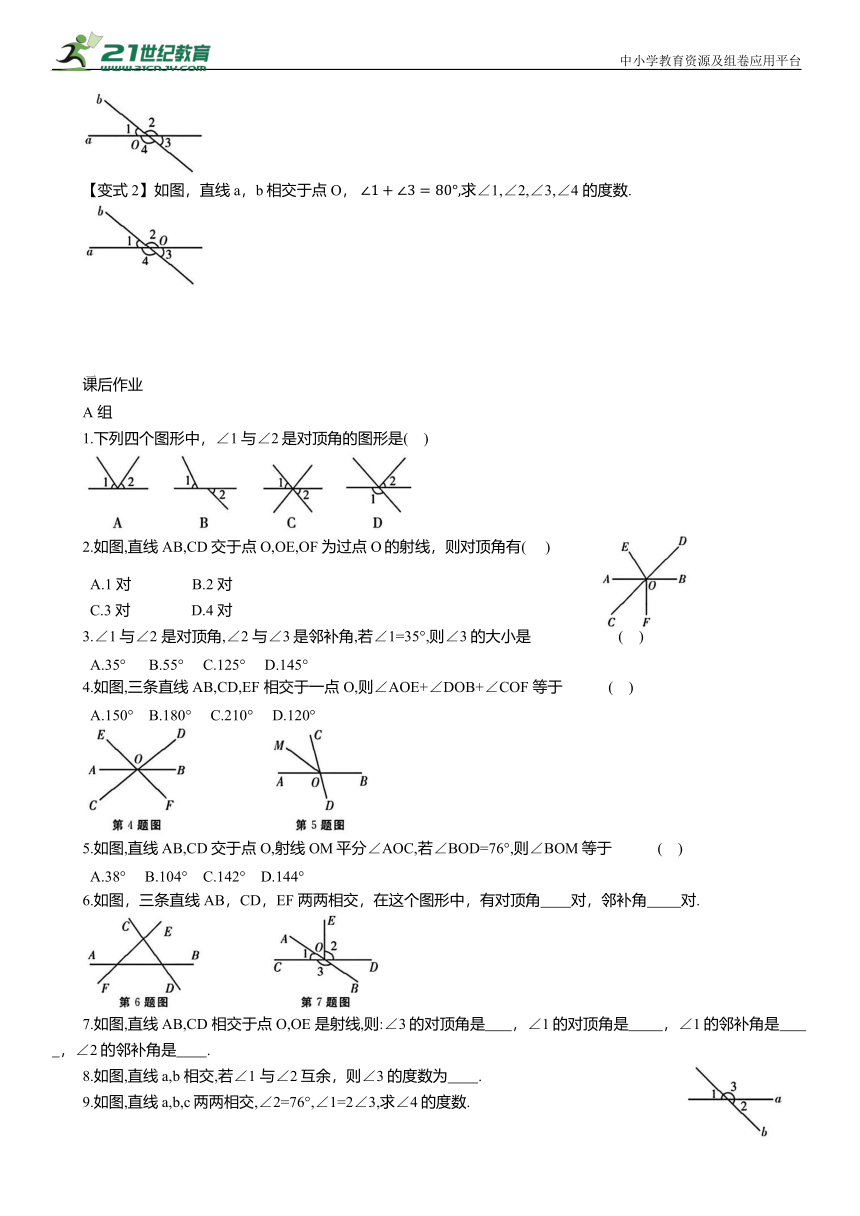
【变式2】如图,直线a,b相交于点O, 求∠1,∠2,∠3,∠4 的度数.
课后作业
A 组
1.下列四个图形中,∠1与∠2是对顶角的图形是( )
2.如图,直线 AB,CD交于点O,OE,OF为过点O的射线,则对顶角有( )
A.1 对 B.2 对
C.3 对 D.4 对
3.∠1与∠2 是对顶角,∠2 与∠3是邻补角,若∠1=35°,则∠3的大小是 ( )
A.35° B.55° C.125° D.145°
4.如图,三条直线 AB,CD,EF 相交于一点 O,则∠AOE+∠DOB+∠COF 等于 ( )
A.150° B.180° C.210° D.120°
5.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于 ( )
A.38° B.104° C.142° D.144°
6.如图,三条直线 AB,CD,EF 两两相交,在这个图形中,有对顶角 对,邻补角 对.
7.如图,直线AB,CD 相交于点O,OE 是射线,则:∠3的对顶角是 ,∠1的对顶角是 ,∠1的邻补角是 ,∠2的邻补角是 .
8.如图,直线a,b 相交,若∠1 与∠2互余,则∠3的度数为 .
9.如图,直线a,b,c两两相交,∠2=76°,∠1=2∠3,求∠4的度数.
B 组
10.如图,直线 AB,CD,EF 相交于点 O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求∠DOE的度数.
11.如图,已知直线 AB 和CD 相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=43°,∠COE =58°,求∠BOE 的度数;
(2)若∠COE : ∠EOB :∠BOD=4 : 3: 2,求∠AOE的度数.
C 组
12.观察,在如图所示的各图中找对顶角(不含平角):
(1)如图a,图中共有 对对顶角.
(2)如图b,图中共有 对对顶角.
(3)如图c,图中共有 对对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有 n条直线相交于一点,则可形成多少对对顶角
(5)若有 2 000条直线相交于一点,则可形成多少对对顶角
第2课时 垂线
基础知识夯实
中小学教育资源及组卷应用平台
知识沉淀
1.垂直的定义:
(1)如图,直线AB,CD 相交于点O,若∠AOC= ,则我们称两条直线互相 ,记作 AB⊥CD.两条直线互相垂直,其中的一条直线叫做另一条直线的 ,它们的交点叫做 .
(2)符号语言:
如图,∵∠AOC=90°,∴ .(垂直的定义)
逆用:∵AB⊥CD,∴∠AOC= .
2.垂线的性质:
(1)在同一平面内,过一点 一条直线与已知直线垂直.
(2)连接直线外一点与直线上各点的所有线段中, 最短.
3.点到直线的距离:直线外一点到这条直线的 的长度,叫做点到直线的距离.
基础过关
1.如图所示,直线 AB,CD 相交于点O,OE⊥CD,已知∠BOE=65°,则∠AOC的大小为 ( )
A.25° B.35°
C.65° D.115°
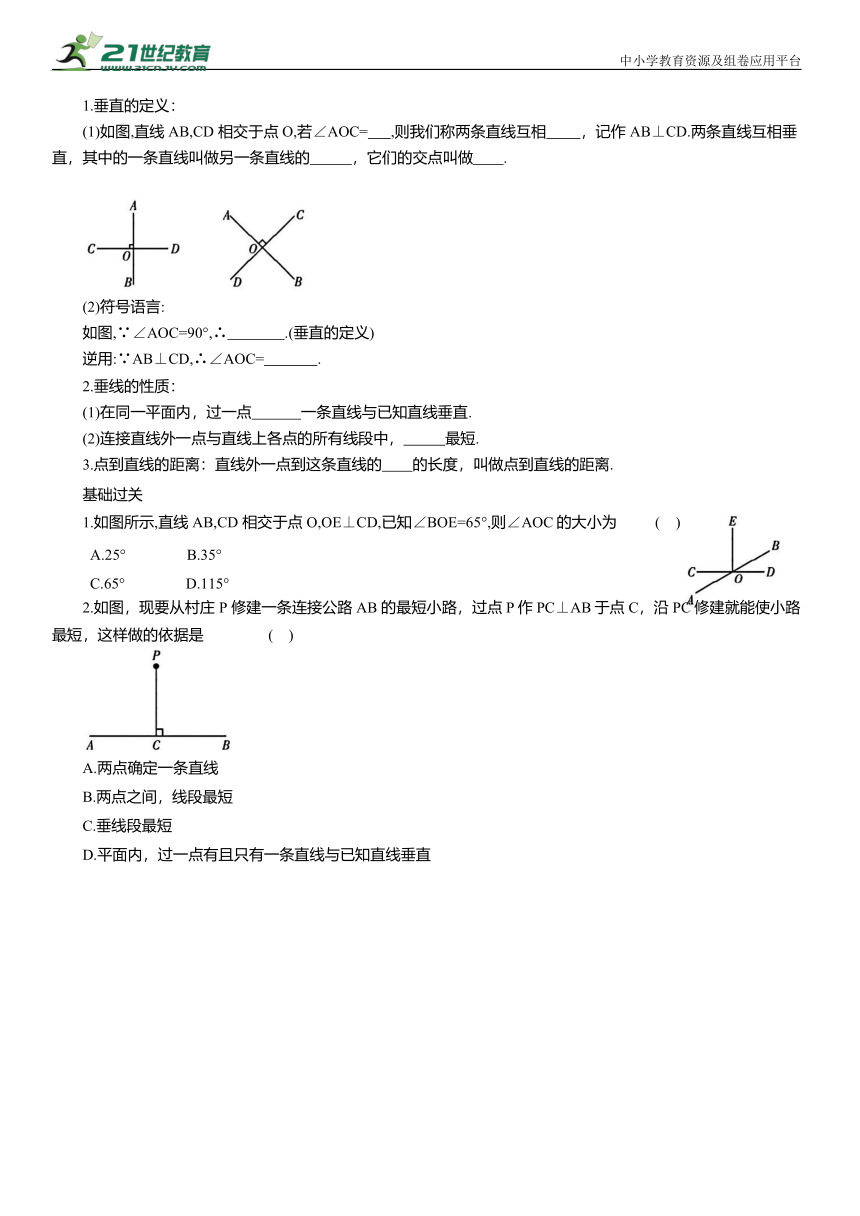
2.如图,现要从村庄 P 修建一条连接公路AB 的最短小路,过点P作PC⊥AB于点C,沿 PC修建就能使小路最短,这样做的依据是 ( )
A.两点确定一条直线
B.两点之间,线段最短
C.垂线段最短
D.平面内,过一点有且只有一条直线与已知直线垂直
典型案例探究
知识点1 垂线的定义
【例题1】如图,已知 DO⊥CO,∠1=35°,∠3=35°.
(1)求∠2的度数;
(2)AO与BO 垂直吗 说明理由.
【变式1】如图,AB⊥CD 于点B,BE是∠ABD的平分线,则∠CBE的度数为 ( )
A.125°
B.130°
C.135°
D.150°
知识点 2 作垂线
【例题2】如图,过点 P 画出射线AB 或线段AB 的垂线.
【变式2】如图,在钝角 AOB 中,点 D 在射线OB 上.
(1)画直线 DE,使 DE⊥OB;
(2)画直线 DF,使 DF⊥OA,垂足为点 F.
知识点 3 点到直线的距离
【例题3】如图,AC⊥BC,C为垂足,CD⊥AB,D 为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC=6,那么:
(1)点C到AB 的距离是 ;
(2)点 A到 BC的距离是 ;
(3)点 B 到CD 的距离是 .
【变式3】如图,AD⊥BD,BC⊥CD,AB=5,BC=3,则BD的长度可能是 ( )
A.2 B.3
C.4 D.5
课后作业
A 组
1.下面说法中正确的是 ( )
A.在同一平面内,两条直线的位置关系有相交、平行、垂直三种
B.在同一平面内,不垂直的两条直线必平行
C.在同一平面内,不平行的两条直线必垂直
D.在同一平面内,不相交的两条直线一定不垂直
2.点到直线的距离是 ( )
A.点到直线上一点的连线
B.点到直线的垂线
C.点到直线的垂线段
D.点到直线的垂线段的长度
3.下列各图中,过直线l外一点画l 的垂线CD,三角板操作正确的是 ( )
4.如图,已知AB⊥CD,垂足为点O,EF为过点O的一条直线,则∠1与∠2 的关系一定成立的是 ( )
A.相等 B.互余
C.互补 D.互为对顶角
如图,把河水引到水池 A 中,可以先引 AB⊥CD,垂足为B,然后沿AB开渠,则能使所开渠最短,这样做的依据是 .
6.如图, ,O 为垂足,若∠BOC=35°,则.
7.如图,O为直线AB 上一点, OC是∠AOD 的平分线.
(1)求∠COD的度数;
(2)试判断OD 与AB 的位置关系.
B 组
8.已知:如图,直线AB,CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
9.如图,直线 AB 与CD 相交于点O,OE 是∠AOC 的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOF的度数;
(2)∠EOF 与∠BOG 是否相等呢 请说明理由;
(3)直接写出图中∠AOE的所有余角.
C 组
10.在如图所示的直角三角形 ABC中,斜边为AB,两直角边分别为AC,BC,设BC=a,AC=b,AB=c.
(1)试用所学知识说明,斜边 AB 是最长的边;
(2)试化简||c-b|+|a-c|+|a+b-c|.
第 3课时 同位角、内错角、同旁内角
基础知识夯实
知识沉淀
1.同位角:如图中的∠1和∠5,这两个角分别在直线AB,CD的同一方(上方),并且都在直线EF 的同侧(右侧),具有这种位置关系的一对角叫做 .图中还有这种位置关系的角有 .
2.内错角:如图中的∠3 和∠5,这两个角都在直线AB,CD之间,并且分别在直线 EF 两侧,具有这种位置关系的一对角叫做 .图中还有这种位置关系的角有 .
3.同旁内角:如图中的∠3 和∠6,这两个角都在直线AB,CD之间,并且都在直线 EF 的同一旁(左侧),具有这种位置关系的一对角叫做 .图中还有这种位置关系的角有 .
基础过关
1.下列各图中的∠1与∠2,哪些是同位角 哪些不是
2.下列各图中的∠1与∠2,哪些是内错角 哪些不是
3.下列各图中的∠1 与∠2,哪些是同旁内角 哪些不是
典型案例探究
知识点 同位角、内错角、同旁内角
【例题】如图,∠A 与∠8 是哪两条直线被第三条直线所截的角 它们是什么关系的角 ∠A 与∠5 呢 ∠A 与∠4 呢
【变式】如图,判断正误(正确的画“ ”,错误的画“×”):
(1)∠B 和∠DAE 是同位角;
(2)∠B 和∠EAC是同位角;
(3)∠B 和∠DAC是同位角;
(4)∠B和∠CAB是同旁内角;
(5)∠B 和∠EAB是同旁内角;
(6)∠B 和∠EAC是内错角;
(7)∠B 和∠DAE是内错角;
(8)∠B 和∠C是同旁内角.
课后作业
A 组
1.如图,三条直线两两相交,则图中∠1 和∠2 是( )
A.同位角 B.内错角
C.同旁内角 D.互为补角
2.若∠α与∠β是同旁内角,且∠α=50°,则∠β的度数是 ( )
A.50° B.130°
C.50°或 130° D.不能确定
3.如图,下列说法错误的是 ( )
A.∠1和∠4是同位角 B.∠1和∠3是同位角
C.∠1 和∠2 是同旁内角 D.∠5 和∠6是内错角
4.如图,构成同旁内角的两个角是 ( )
A.∠1 和∠5 B.∠4 和∠5
C.∠7 和∠8 D.∠3 和∠6
5.下列图形中,∠1与∠2是同位角的是 ( )
A.②③ B.②③④ C.①②④ D.③④
6.如图,∠B 与∠CAD 是由直线 和直线 被直线 所截得到的 角.
7.如图,按角的位置关系填空:∠A与∠1是 ;∠A 与∠3是 ;∠2与∠3是 .
8.如图, 是∠1 和∠6 的同位角, 是∠1 和∠6的内错角, 是∠6的同旁内角.
9.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3 的同旁内角等于 .
10.如图,标有角号的7 个角中共有 对内错角, 对同位角, 对同旁内角.
11.根据图形说出下列各对角是什么位置关系
(1)∠1和∠2;(2)∠1 和∠7;(3)∠3 和∠4;(4)∠4和∠6;(5)∠5和∠7.
12.如图, 和 是哪两条直线被哪一条直线所截形成的 它们是什么角 ∠1和∠3是哪两条直线被哪一条直线所截形成的 它们是什么角
C 组
13.如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上.例如:从起始位置∠1跳到终点位置∠3,写出其中两种不同路径,路径1:∠1
(1)从起始∠1跳到终点∠8,试写出一种路径;
(2)从起始∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8
基础过关
1.在同一平面内,直线 l 与l 满足下列条件,写出其对应的位置关系.
(1)l 与l 没有公共点,则l 与l ;
(2) l 与 l 有 且 只 有 一 个 公 共 点, 则 l 与l ;
(3)l 与l 有两个公共点,则l 与l .
2.下列语句中正确的有 ( )
①任意两条直线的位置关系不是相交就是平行;
②过一点有且只有一条直线和已知直线平行;
③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b;
④若直线a∥b,b∥c,则c∥a.
A.4个 B.3个 C.2个 D.1 个
5.1 相交线
第 1课时 相交线
【基础知识夯实】
知识沉淀
1.(1)邻补角 ∠1 和∠4,∠3 和∠4,∠3 和∠2
(2)互补
2.(1)对顶角 ∠2 和∠4 (2)相等
基础过关
1.(1)不是 (2)不是 (3)是
2.(1)不是 (2)是 (3)不是 (4)不是 (5)是
【典型案例探究】
例题1 解:互为邻补角的有:∠AOE 和∠BOE,∠AOD和∠BOD,∠AOC 和∠BOC,∠AOC 和∠AOD,∠COE和∠DOE,∠BOC和∠BOD.
互为对顶角的有:∠AOD 和∠BOC,∠AOC和∠BOD.
变式1∠FOB ∠FOD,∠COE
例题2解:由邻补角定义,可得
由对顶角相等,可得
∠3=∠1=30°,∠4=∠2=150°.
变式2 ∠3=∠1=40°,∠4=∠2=140°.
【课后作业】
1. C 2. B 3. D 4. B 5. C 6.6 12
7.∠AOD ∠BOD ∠3,∠AOD ∠COE
8.135°
9.解:因为∠2=76°,所以∠1=∠2=76°.
因为∠1=2∠3,所以
所以∠4=180°-∠3=142°.
10.解:∵∠AOE:∠AOD=1:3,
∴设∠AOE=k,∠AOD=3k.
则∠COB=∠AOD=3k.
∵∠COB:∠DOF=3:4,
∴∠DOF=4k.
∴∠AOE+∠AOD+∠DOF=k+3k+4k=180°.
解得k=22.5°.
∴∠DOE=∠AOE+∠AOD=k+3k=4k=4×22.5°=90°.即∠DOE=90°.
11.解:(1)因为∠AOC=43°,∠COE=58°.
所以∠BOE=180°—∠AOC-∠COE=180°-43°—
(2)因为∠COE:∠EOB:∠BOD=4:3:2,∠COE+∠EOB+∠BOD=180°,
所以
所以∠AOC=∠BOD=40°.
所以
12.解:(1)2 (2)6 (3)12
(4)2×1=2,3×(3-1)=6,4×(4-1)=12,
所以若有n条直线相交于一点,则可形成n(n-1)对对顶角.
(5)2 000×(2 000-1)=3 998 000,
若有2000条直线相交于一点,则可形成3998 000对对顶角.
第 2 课时 垂线
【基础知识夯实】
知识沉淀
1.(1)90°垂直垂线 垂足 (2)AB⊥CD 90°
2.(1)有且只有 (2)垂线段 3.垂线段
基础过关
1. A 2. C
【典型案例探究】
例题1解:(1)因为 DO⊥CO,所以∠COD=90°.
所以∠2=∠COD-∠1=55°.
(2)因为∠2=55°,∠3=35°,
所以∠AOB=∠2+∠3=90°.
所以 AO与BO 垂直.
变式1 C
例题2
变式2
例题3 (1)4.8 (2)6 (3)6.4
变式3 C
【课后作业】
1. D 2. D 3. D 4. B 5.垂线段最短 6.145°
7.解:(1)∵∠AOC= ∠BOC,∠AOC与∠BOC互补,
∴∠AOC+∠BOC=∠AOC+3∠AOC=180°.
∴∠AOC=45°.
又∵OC是∠AOD的平分线,
∴∠COD=∠AOC=45°.
(2)由(1),得∠COD=∠AOC=45°,
∴∠AOD=∠COD+∠AOC=90°.
∴OD 与 AB 互相垂直.
8.解:(1)∵∠AOC=36°,∠COE=90°.
∴∠BOE=180°-∠AOC-∠COE=54°.
(2)∵∠BOD:∠BOC=1: 5.
∴∠AOC=30°.
(3)∠EOF 的度数是 30°或 150°.
9.解:(1)∵OF⊥CD,
∴∠COF=90°.
又∵∠AOC与∠BOD 是对顶角,
∴∠AOC=∠BOD=52°.
∴∠AOF=∠COF-∠AOC=90°-52°=38°.
(2)相等.理由如下:∵∠AOC与∠BOD是对顶角.
∴∠AOC=∠BOD=52°.
∵OE 是∠AOC的平分线,∴
又∵OG⊥OE,∴∠EOG=90°.
∴∠BOG=180°-∠AOE-∠EOG=64°.
∵∠EOF=∠AOF+∠AOE=38°+26°=64°,
∴∠EOF=∠BOG.
(3)图中∠AOE的所有余角为∠EOF,∠COG,∠BOG.
10.解:(1)因为点 A 与直线BC 上点B,C的连线中,AC是垂线段,所以 AC因为点 B与直线AC 上点A,C的连线中,BC是垂线段,所以 BC故 AB,AC,BC中,斜边 AB最长.
(2)因为ACAB,即a+b>c.
所以原式=c-b+(c-a)+a+b-c=c.
第3 课时 同位角、内错角、同旁内角
【基础知识夯实】
知识沉淀
1.同位角 ∠2和∠6,∠3 和∠7,∠4 和∠8
2.内错角 ∠4 和∠6
3.同旁内角 ∠4 和∠5
基础过关
1.(1)是 (2)是 (3)不是
2.(1)是 (2)不是 (3)不是
3.(1)是 (2)是 (3)不是
【典型案例探究】
例题 (1)AB 与DE 被AC 所截,是内错角.
(2)AB 与 DE 被AC 所截,是同旁内角.
(3)AC与 DE 被AB 所截,是同位角.
变式 (1) (2)× (3) (4)
(5) (6)× (7)× (8)
【课后作业】
1. B 2. D 3. A 4. A 5. C
6. BC AC BD 同位
7.同旁内角 同位角 内错角
8.∠3 ∠5 ∠4 9.80° 80° 100°
10.42 4
11.解:(1)∠1和∠2 是同旁内角.
(2)∠1 和∠7 是同位角.
(3)∠3 和∠4是内错角.
(4)∠4 和∠6是同旁内角.
(5)∠5 和∠7 是内错角.
12.解:∠1和∠2是直线EF,DC被直线AB 所截形成的同位角,∠1和∠3是直线AB,CD被直线EF 所截形成的同位角.
13.解:一)
(2)从起始∠1依次按同位角、内错角、同旁内角的顺
5.1相交线同步课时练习
第 1课时 相交线
基础知识夯实
知识沉淀
1.邻补角:
(1)概念:如图,∠1 和∠2 有一条公共边 OC,它们的另一边互为反向延长线(∠1 和∠2 互补),具有这种关系的两个角,互为 .图中还有其他的邻补角: .
(2)性质:邻补角 .
2.对顶角:
(1)概念:如图,∠1和∠3 有一个公共顶点 O,并且∠1 的两边分别是∠3的两边的反向延长线,具有这种位置关系的两个角,互为 .图中还有其他的对顶角: .
(2)性质:对顶角 .
基础过关
1.下列各图中,∠1 和∠2 是邻补角吗 为什么
2.下列各图中,∠1 和∠2 是对顶角吗 为什么
典型案例探究
知识点1 邻补角、对顶角的定义
【例题1】如图,直线 AB,CD 交于点O,OE 为以点O为端点的射线,写出图中所有的邻补角和对顶角.
【变式1】如图,三条直线 AB ,CD ,EF 相交于点O,∠AOE 的对顶角是 ,∠EOD 的邻补角是 .
知识点 2 邻补角、对顶角的性质
【例题2】如图,直线a,b相交于点O,∠1=30°,求∠2,∠3,∠4的度数.
【变式2】如图,直线a,b相交于点O, 求∠1,∠2,∠3,∠4 的度数.
课后作业
A 组
1.下列四个图形中,∠1与∠2是对顶角的图形是( )
2.如图,直线 AB,CD交于点O,OE,OF为过点O的射线,则对顶角有( )
A.1 对 B.2 对
C.3 对 D.4 对
3.∠1与∠2 是对顶角,∠2 与∠3是邻补角,若∠1=35°,则∠3的大小是 ( )
A.35° B.55° C.125° D.145°
4.如图,三条直线 AB,CD,EF 相交于一点 O,则∠AOE+∠DOB+∠COF 等于 ( )
A.150° B.180° C.210° D.120°
5.如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于 ( )
A.38° B.104° C.142° D.144°
6.如图,三条直线 AB,CD,EF 两两相交,在这个图形中,有对顶角 对,邻补角 对.
7.如图,直线AB,CD 相交于点O,OE 是射线,则:∠3的对顶角是 ,∠1的对顶角是 ,∠1的邻补角是 ,∠2的邻补角是 .
8.如图,直线a,b 相交,若∠1 与∠2互余,则∠3的度数为 .
9.如图,直线a,b,c两两相交,∠2=76°,∠1=2∠3,求∠4的度数.
B 组
10.如图,直线 AB,CD,EF 相交于点 O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求∠DOE的度数.
11.如图,已知直线 AB 和CD 相交于点O,在∠COB的内部作射线OE.
(1)若∠AOC=43°,∠COE =58°,求∠BOE 的度数;
(2)若∠COE : ∠EOB :∠BOD=4 : 3: 2,求∠AOE的度数.
C 组
12.观察,在如图所示的各图中找对顶角(不含平角):
(1)如图a,图中共有 对对顶角.
(2)如图b,图中共有 对对顶角.
(3)如图c,图中共有 对对顶角.
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有 n条直线相交于一点,则可形成多少对对顶角
(5)若有 2 000条直线相交于一点,则可形成多少对对顶角
第2课时 垂线
基础知识夯实
中小学教育资源及组卷应用平台
知识沉淀
1.垂直的定义:
(1)如图,直线AB,CD 相交于点O,若∠AOC= ,则我们称两条直线互相 ,记作 AB⊥CD.两条直线互相垂直,其中的一条直线叫做另一条直线的 ,它们的交点叫做 .
(2)符号语言:
如图,∵∠AOC=90°,∴ .(垂直的定义)
逆用:∵AB⊥CD,∴∠AOC= .
2.垂线的性质:
(1)在同一平面内,过一点 一条直线与已知直线垂直.
(2)连接直线外一点与直线上各点的所有线段中, 最短.
3.点到直线的距离:直线外一点到这条直线的 的长度,叫做点到直线的距离.
基础过关
1.如图所示,直线 AB,CD 相交于点O,OE⊥CD,已知∠BOE=65°,则∠AOC的大小为 ( )
A.25° B.35°
C.65° D.115°
2.如图,现要从村庄 P 修建一条连接公路AB 的最短小路,过点P作PC⊥AB于点C,沿 PC修建就能使小路最短,这样做的依据是 ( )
A.两点确定一条直线
B.两点之间,线段最短
C.垂线段最短
D.平面内,过一点有且只有一条直线与已知直线垂直
典型案例探究
知识点1 垂线的定义
【例题1】如图,已知 DO⊥CO,∠1=35°,∠3=35°.
(1)求∠2的度数;
(2)AO与BO 垂直吗 说明理由.
【变式1】如图,AB⊥CD 于点B,BE是∠ABD的平分线,则∠CBE的度数为 ( )
A.125°
B.130°
C.135°
D.150°
知识点 2 作垂线
【例题2】如图,过点 P 画出射线AB 或线段AB 的垂线.
【变式2】如图,在钝角 AOB 中,点 D 在射线OB 上.
(1)画直线 DE,使 DE⊥OB;
(2)画直线 DF,使 DF⊥OA,垂足为点 F.
知识点 3 点到直线的距离
【例题3】如图,AC⊥BC,C为垂足,CD⊥AB,D 为垂足,BC=8,CD=4.8,BD=6.4,AD=3.6,AC=6,那么:
(1)点C到AB 的距离是 ;
(2)点 A到 BC的距离是 ;
(3)点 B 到CD 的距离是 .
【变式3】如图,AD⊥BD,BC⊥CD,AB=5,BC=3,则BD的长度可能是 ( )
A.2 B.3
C.4 D.5
课后作业
A 组
1.下面说法中正确的是 ( )
A.在同一平面内,两条直线的位置关系有相交、平行、垂直三种
B.在同一平面内,不垂直的两条直线必平行
C.在同一平面内,不平行的两条直线必垂直
D.在同一平面内,不相交的两条直线一定不垂直
2.点到直线的距离是 ( )
A.点到直线上一点的连线
B.点到直线的垂线
C.点到直线的垂线段
D.点到直线的垂线段的长度
3.下列各图中,过直线l外一点画l 的垂线CD,三角板操作正确的是 ( )
4.如图,已知AB⊥CD,垂足为点O,EF为过点O的一条直线,则∠1与∠2 的关系一定成立的是 ( )
A.相等 B.互余
C.互补 D.互为对顶角
如图,把河水引到水池 A 中,可以先引 AB⊥CD,垂足为B,然后沿AB开渠,则能使所开渠最短,这样做的依据是 .
6.如图, ,O 为垂足,若∠BOC=35°,则.
7.如图,O为直线AB 上一点, OC是∠AOD 的平分线.
(1)求∠COD的度数;
(2)试判断OD 与AB 的位置关系.
B 组
8.已知:如图,直线AB,CD相交于点O,∠COE=90°.
(1)若∠AOC=36°,求∠BOE的度数;
(2)若∠BOD:∠BOC=1:5,求∠AOE的度数;
(3)在(2)的条件下,过点O作OF⊥AB,请直接写出∠EOF的度数.
9.如图,直线 AB 与CD 相交于点O,OE 是∠AOC 的平分线,OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOF的度数;
(2)∠EOF 与∠BOG 是否相等呢 请说明理由;
(3)直接写出图中∠AOE的所有余角.
C 组
10.在如图所示的直角三角形 ABC中,斜边为AB,两直角边分别为AC,BC,设BC=a,AC=b,AB=c.
(1)试用所学知识说明,斜边 AB 是最长的边;
(2)试化简||c-b|+|a-c|+|a+b-c|.
第 3课时 同位角、内错角、同旁内角
基础知识夯实
知识沉淀
1.同位角:如图中的∠1和∠5,这两个角分别在直线AB,CD的同一方(上方),并且都在直线EF 的同侧(右侧),具有这种位置关系的一对角叫做 .图中还有这种位置关系的角有 .
2.内错角:如图中的∠3 和∠5,这两个角都在直线AB,CD之间,并且分别在直线 EF 两侧,具有这种位置关系的一对角叫做 .图中还有这种位置关系的角有 .
3.同旁内角:如图中的∠3 和∠6,这两个角都在直线AB,CD之间,并且都在直线 EF 的同一旁(左侧),具有这种位置关系的一对角叫做 .图中还有这种位置关系的角有 .
基础过关
1.下列各图中的∠1与∠2,哪些是同位角 哪些不是
2.下列各图中的∠1与∠2,哪些是内错角 哪些不是
3.下列各图中的∠1 与∠2,哪些是同旁内角 哪些不是
典型案例探究
知识点 同位角、内错角、同旁内角
【例题】如图,∠A 与∠8 是哪两条直线被第三条直线所截的角 它们是什么关系的角 ∠A 与∠5 呢 ∠A 与∠4 呢
【变式】如图,判断正误(正确的画“ ”,错误的画“×”):
(1)∠B 和∠DAE 是同位角;
(2)∠B 和∠EAC是同位角;
(3)∠B 和∠DAC是同位角;
(4)∠B和∠CAB是同旁内角;
(5)∠B 和∠EAB是同旁内角;
(6)∠B 和∠EAC是内错角;
(7)∠B 和∠DAE是内错角;
(8)∠B 和∠C是同旁内角.
课后作业
A 组
1.如图,三条直线两两相交,则图中∠1 和∠2 是( )
A.同位角 B.内错角
C.同旁内角 D.互为补角
2.若∠α与∠β是同旁内角,且∠α=50°,则∠β的度数是 ( )
A.50° B.130°
C.50°或 130° D.不能确定
3.如图,下列说法错误的是 ( )
A.∠1和∠4是同位角 B.∠1和∠3是同位角
C.∠1 和∠2 是同旁内角 D.∠5 和∠6是内错角
4.如图,构成同旁内角的两个角是 ( )
A.∠1 和∠5 B.∠4 和∠5
C.∠7 和∠8 D.∠3 和∠6
5.下列图形中,∠1与∠2是同位角的是 ( )
A.②③ B.②③④ C.①②④ D.③④
6.如图,∠B 与∠CAD 是由直线 和直线 被直线 所截得到的 角.
7.如图,按角的位置关系填空:∠A与∠1是 ;∠A 与∠3是 ;∠2与∠3是 .
8.如图, 是∠1 和∠6 的同位角, 是∠1 和∠6的内错角, 是∠6的同旁内角.
9.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3 的同旁内角等于 .
10.如图,标有角号的7 个角中共有 对内错角, 对同位角, 对同旁内角.
11.根据图形说出下列各对角是什么位置关系
(1)∠1和∠2;(2)∠1 和∠7;(3)∠3 和∠4;(4)∠4和∠6;(5)∠5和∠7.
12.如图, 和 是哪两条直线被哪一条直线所截形成的 它们是什么角 ∠1和∠3是哪两条直线被哪一条直线所截形成的 它们是什么角
C 组
13.如图是一个跳棋棋盘,其游戏规则是:一个棋子从某一个起始角开始,经过若干步跳动以后,到达终点角.跳动时,每一步只能跳到它的同位角或内错角或同旁内角的位置上.例如:从起始位置∠1跳到终点位置∠3,写出其中两种不同路径,路径1:∠1
(1)从起始∠1跳到终点∠8,试写出一种路径;
(2)从起始∠1依次按同位角、内错角、同旁内角的顺序跳,能否跳到终点∠8
基础过关
1.在同一平面内,直线 l 与l 满足下列条件,写出其对应的位置关系.
(1)l 与l 没有公共点,则l 与l ;
(2) l 与 l 有 且 只 有 一 个 公 共 点, 则 l 与l ;
(3)l 与l 有两个公共点,则l 与l .
2.下列语句中正确的有 ( )
①任意两条直线的位置关系不是相交就是平行;
②过一点有且只有一条直线和已知直线平行;
③过两条直线a,b外一点P,画直线c,使c∥a,且c∥b;
④若直线a∥b,b∥c,则c∥a.
A.4个 B.3个 C.2个 D.1 个
5.1 相交线
第 1课时 相交线
【基础知识夯实】
知识沉淀
1.(1)邻补角 ∠1 和∠4,∠3 和∠4,∠3 和∠2
(2)互补
2.(1)对顶角 ∠2 和∠4 (2)相等
基础过关
1.(1)不是 (2)不是 (3)是
2.(1)不是 (2)是 (3)不是 (4)不是 (5)是
【典型案例探究】
例题1 解:互为邻补角的有:∠AOE 和∠BOE,∠AOD和∠BOD,∠AOC 和∠BOC,∠AOC 和∠AOD,∠COE和∠DOE,∠BOC和∠BOD.
互为对顶角的有:∠AOD 和∠BOC,∠AOC和∠BOD.
变式1∠FOB ∠FOD,∠COE
例题2解:由邻补角定义,可得
由对顶角相等,可得
∠3=∠1=30°,∠4=∠2=150°.
变式2 ∠3=∠1=40°,∠4=∠2=140°.
【课后作业】
1. C 2. B 3. D 4. B 5. C 6.6 12
7.∠AOD ∠BOD ∠3,∠AOD ∠COE
8.135°
9.解:因为∠2=76°,所以∠1=∠2=76°.
因为∠1=2∠3,所以
所以∠4=180°-∠3=142°.
10.解:∵∠AOE:∠AOD=1:3,
∴设∠AOE=k,∠AOD=3k.
则∠COB=∠AOD=3k.
∵∠COB:∠DOF=3:4,
∴∠DOF=4k.
∴∠AOE+∠AOD+∠DOF=k+3k+4k=180°.
解得k=22.5°.
∴∠DOE=∠AOE+∠AOD=k+3k=4k=4×22.5°=90°.即∠DOE=90°.
11.解:(1)因为∠AOC=43°,∠COE=58°.
所以∠BOE=180°—∠AOC-∠COE=180°-43°—
(2)因为∠COE:∠EOB:∠BOD=4:3:2,∠COE+∠EOB+∠BOD=180°,
所以
所以∠AOC=∠BOD=40°.
所以
12.解:(1)2 (2)6 (3)12
(4)2×1=2,3×(3-1)=6,4×(4-1)=12,
所以若有n条直线相交于一点,则可形成n(n-1)对对顶角.
(5)2 000×(2 000-1)=3 998 000,
若有2000条直线相交于一点,则可形成3998 000对对顶角.
第 2 课时 垂线
【基础知识夯实】
知识沉淀
1.(1)90°垂直垂线 垂足 (2)AB⊥CD 90°
2.(1)有且只有 (2)垂线段 3.垂线段
基础过关
1. A 2. C
【典型案例探究】
例题1解:(1)因为 DO⊥CO,所以∠COD=90°.
所以∠2=∠COD-∠1=55°.
(2)因为∠2=55°,∠3=35°,
所以∠AOB=∠2+∠3=90°.
所以 AO与BO 垂直.
变式1 C
例题2
变式2
例题3 (1)4.8 (2)6 (3)6.4
变式3 C
【课后作业】
1. D 2. D 3. D 4. B 5.垂线段最短 6.145°
7.解:(1)∵∠AOC= ∠BOC,∠AOC与∠BOC互补,
∴∠AOC+∠BOC=∠AOC+3∠AOC=180°.
∴∠AOC=45°.
又∵OC是∠AOD的平分线,
∴∠COD=∠AOC=45°.
(2)由(1),得∠COD=∠AOC=45°,
∴∠AOD=∠COD+∠AOC=90°.
∴OD 与 AB 互相垂直.
8.解:(1)∵∠AOC=36°,∠COE=90°.
∴∠BOE=180°-∠AOC-∠COE=54°.
(2)∵∠BOD:∠BOC=1: 5.
∴∠AOC=30°.
(3)∠EOF 的度数是 30°或 150°.
9.解:(1)∵OF⊥CD,
∴∠COF=90°.
又∵∠AOC与∠BOD 是对顶角,
∴∠AOC=∠BOD=52°.
∴∠AOF=∠COF-∠AOC=90°-52°=38°.
(2)相等.理由如下:∵∠AOC与∠BOD是对顶角.
∴∠AOC=∠BOD=52°.
∵OE 是∠AOC的平分线,∴
又∵OG⊥OE,∴∠EOG=90°.
∴∠BOG=180°-∠AOE-∠EOG=64°.
∵∠EOF=∠AOF+∠AOE=38°+26°=64°,
∴∠EOF=∠BOG.
(3)图中∠AOE的所有余角为∠EOF,∠COG,∠BOG.
10.解:(1)因为点 A 与直线BC 上点B,C的连线中,AC是垂线段,所以 AC
(2)因为AC
所以原式=c-b+(c-a)+a+b-c=c.
第3 课时 同位角、内错角、同旁内角
【基础知识夯实】
知识沉淀
1.同位角 ∠2和∠6,∠3 和∠7,∠4 和∠8
2.内错角 ∠4 和∠6
3.同旁内角 ∠4 和∠5
基础过关
1.(1)是 (2)是 (3)不是
2.(1)是 (2)不是 (3)不是
3.(1)是 (2)是 (3)不是
【典型案例探究】
例题 (1)AB 与DE 被AC 所截,是内错角.
(2)AB 与 DE 被AC 所截,是同旁内角.
(3)AC与 DE 被AB 所截,是同位角.
变式 (1) (2)× (3) (4)
(5) (6)× (7)× (8)
【课后作业】
1. B 2. D 3. A 4. A 5. C
6. BC AC BD 同位
7.同旁内角 同位角 内错角
8.∠3 ∠5 ∠4 9.80° 80° 100°
10.42 4
11.解:(1)∠1和∠2 是同旁内角.
(2)∠1 和∠7 是同位角.
(3)∠3 和∠4是内错角.
(4)∠4 和∠6是同旁内角.
(5)∠5 和∠7 是内错角.
12.解:∠1和∠2是直线EF,DC被直线AB 所截形成的同位角,∠1和∠3是直线AB,CD被直线EF 所截形成的同位角.
13.解:一)
(2)从起始∠1依次按同位角、内错角、同旁内角的顺
