7.1 平面直角坐标系课时同步练习(含答案)
文档属性
| 名称 | 7.1 平面直角坐标系课时同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 10:11:31 | ||
图片预览


文档简介
第七章 平面直角坐标系
7.1 平面直角坐标系
第1课时 有序数对
基础知识夯实
中小学教育资源及组卷应用平台
知识沉淀
有序数对:有 的两个数a与b组成的数对,叫做有序数对,记作(a,b).
注:利用有序数对,可以准确地表示出一个位置.
基础过关
如图,小鸡的位置可以用有序数对(2,3)表示,请说出图中其他物体位置.
苹果: ;足球: ;
花朵: ;香蕉: .
典型案例探究
知识点 1 根据位置写出有序数对
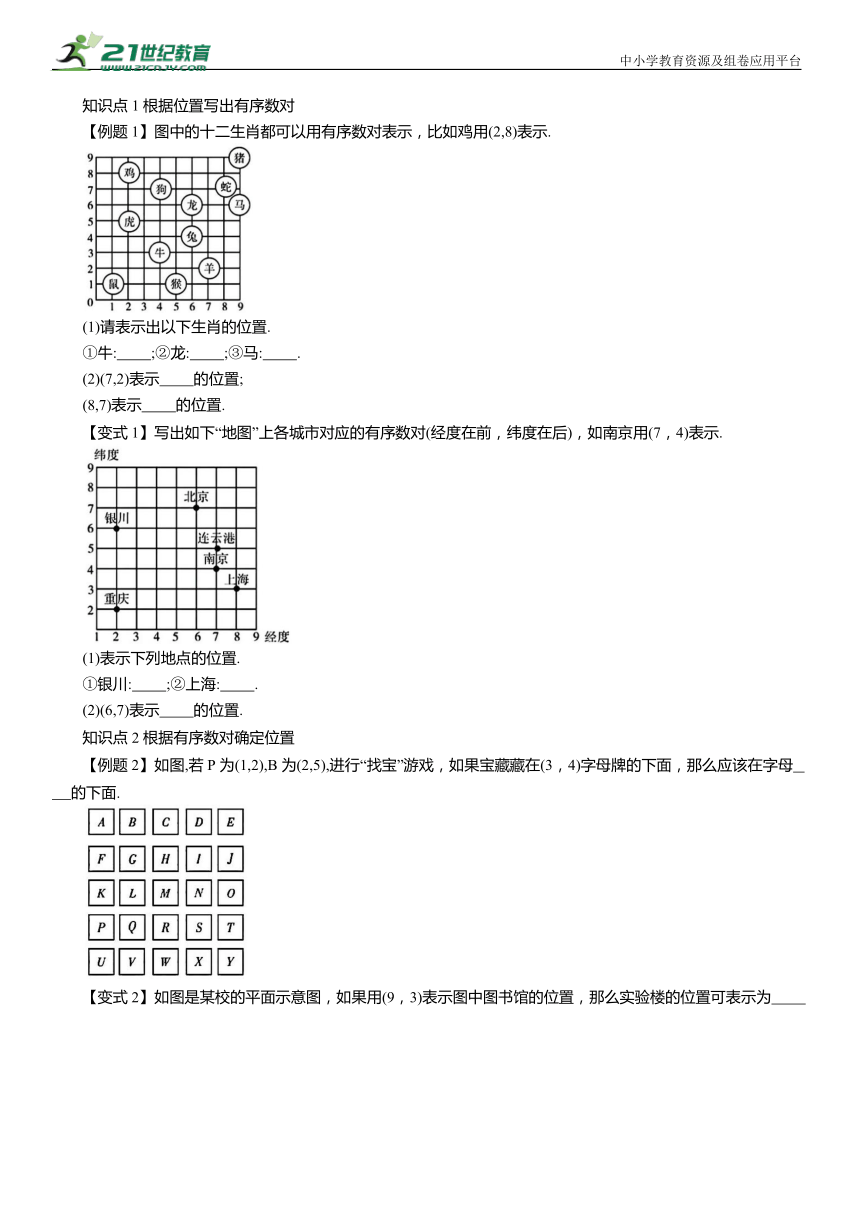
【例题1】图中的十二生肖都可以用有序数对表示,比如鸡用(2,8)表示.
(1)请表示出以下生肖的位置.
①牛: ;②龙: ;③马: .
(2)(7,2)表示 的位置;
(8,7)表示 的位置.
【变式1】写出如下“地图”上各城市对应的有序数对(经度在前,纬度在后),如南京用(7,4)表示.
(1)表示下列地点的位置.
①银川: ;②上海: .
(2)(6,7)表示 的位置.
知识点 2 根据有序数对确定位置
【例题2】如图,若P 为(1,2),B 为(2,5),进行“找宝”游戏,如果宝藏藏在(3,4)字母牌的下面,那么应该在字母 的下面.
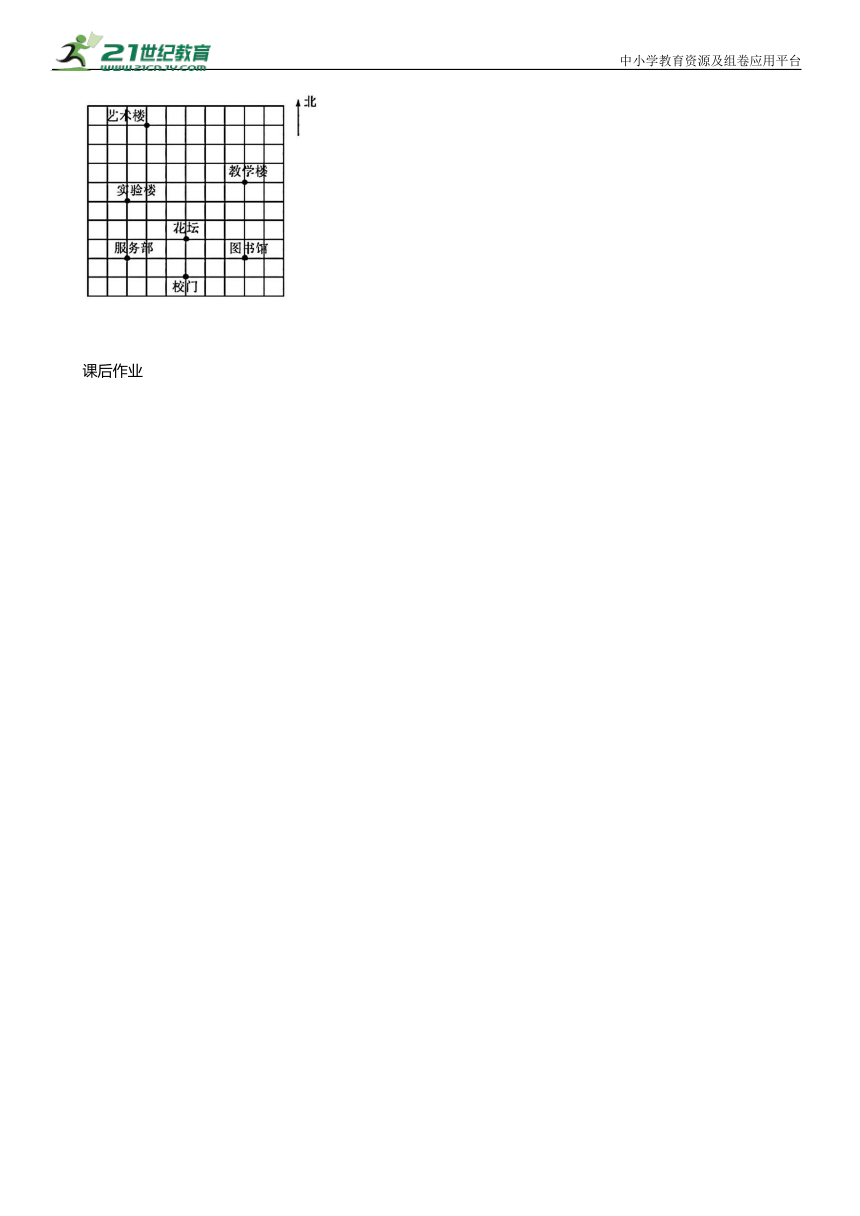
【变式2】如图是某校的平面示意图,如果用(9,3)表示图中图书馆的位置,那么实验楼的位置可表示为
课后作业
A 组
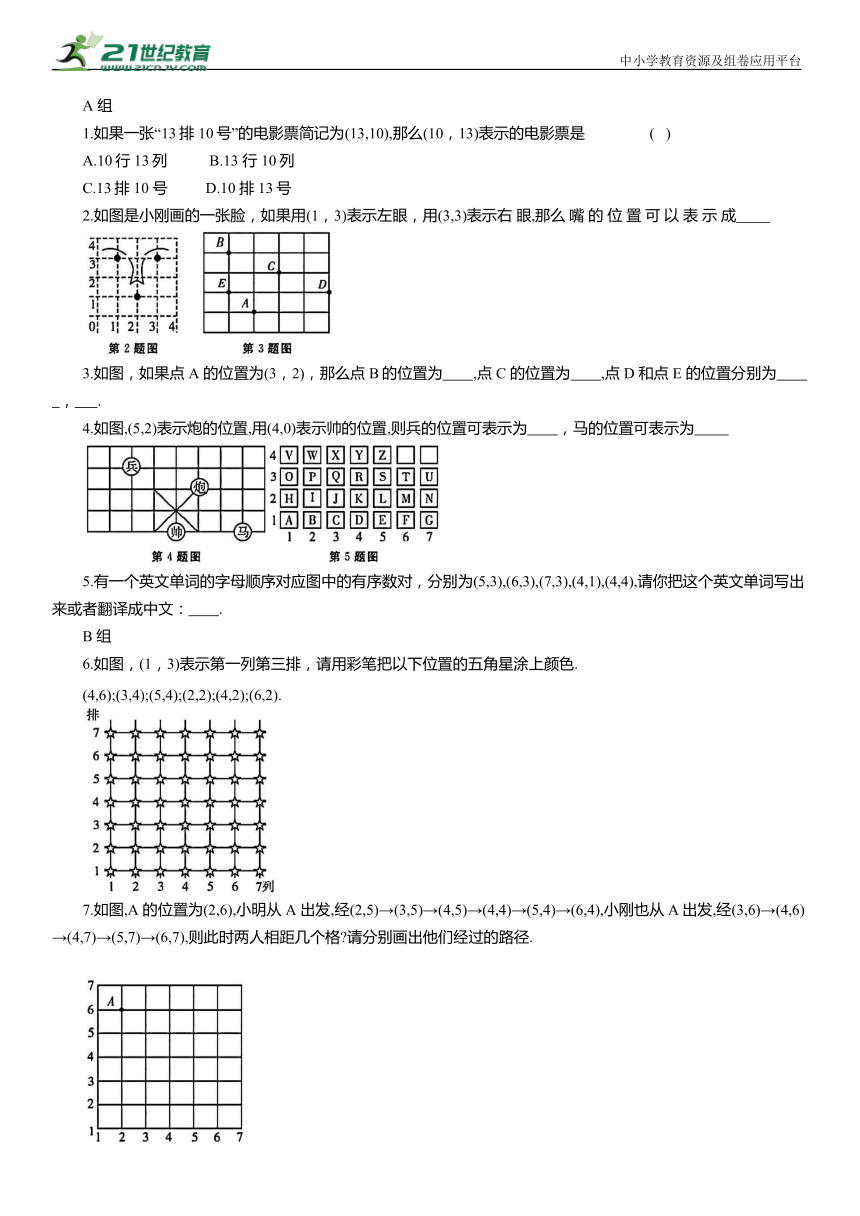
1.如果一张“13排10号”的电影票简记为(13,10),那么(10,13)表示的电影票是 ( )
A.10行13列 B.13 行 10列
C.13排 10 号 D.10 排13号
2.如图是小刚画的一张脸,如果用(1,3)表示左眼,用(3,3)表示右 眼,那么 嘴 的 位 置 可 以 表 示 成
3.如图,如果点 A 的位置为(3,2),那么点 B的位置为 ,点 C 的位置为 ,点 D 和点 E 的位置分别为 , .
4.如图,(5,2)表示炮的位置,用(4,0)表示帅的位置,则兵的位置可表示为 ,马的位置可表示为
5.有一个英文单词的字母顺序对应图中的有序数对,分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文: .
B 组
6.如图,(1,3)表示第一列第三排,请用彩笔把以下位置的五角星涂上颜色.
(4,6);(3,4);(5,4);(2,2);(4,2);(6,2).
7.如图,A 的位置为(2,6),小明从 A 出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格 请分别画出他们经过的路径.
8.如图,若点A(2,1)表示放置2 个胡萝卜,1 棵青菜;点 B(4,2)表示放置4个胡萝卜,2 棵青菜.
(1)请写出点C所表示的意义;
(2)若一只小兔子从 A到达B(顺着方格线走)有以下几种路径可选择:
①A→C→D→B;②A→E→D→B;③A→E→F→B.则走哪条路径吃到胡萝卜最多 走哪条路径吃到青菜最多
C 组
9.如图,点 A 表示3 街与 5 大道的十字路口,点 B表示 5 街与 3 大道的十字路口,如果用(3,5)→(4,5)→(5,5)→(5,4)→(5,3)表示由 A到B 的一条路径,那么从A到B 共有几条路径(只能向右或向下走) 请写出其中1条路径.
第 2 课时 平面直角坐标系(1)——点的坐标
基础知识夯实
知识沉淀
1.平面直角坐标系:
(1)在平面内,由两条互相垂直、原点重合的数轴组成平面直角坐标系,其中水平的数轴称为x 轴或 ,习惯上取向 为正方向;竖直的数轴称为y轴或 ,取向 为正方向;两坐标轴的交点为平面直角坐标系的原点.
(2)对于平面内任意一点 P,过点 P 分别向x 轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点 P 的 、 ,有序数对(a,b)叫做点 P 的 .
2.如图,填空:
点 B的坐标为 ,其中横坐标为 ,纵坐标为 ;点C的坐标为 .
3.点(x,y)到x 轴的距离是|y|,到 y 轴的距离是 ·
基础过关
1.点C的横坐标是-4,纵坐标是1,则点 C 的坐标记作 .
2.如图,请写出点 A,B,C的坐标: .
3.(1)P点的坐标为(—4,—5),则点 P 到x 轴的距离为 ,点 P 到y 轴的距离为 .
(2)点A(3,—4)到x轴的距离是 ( )
A.-4 B.3 C.5 D.4
典型案例探究
知识点 1 根据点的位置写出坐标
【例题1】如图,写出下列各点的坐标:
A点( —1 , —1 ),
B点 ,C点 ,
D点 ,E点 ,
F点 ,G点 ,
H 点 .
知识点 2 根据坐标确定点的位置
【例题2】在如图所示的平面直角坐标系中描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(3,-2),E(0,-4),F(-2,0),G(4,0),H(0,3).
【变式1】如图,写出下列各点坐标.
【变式2】在如图所示的平面直角坐标系中描出下列各点:
A(2,3),B(-2,3),C(3,-5),
D(-4,-5),E(0,-3),F(5,0),
课后作业
A 组
1.如图,在平面直角坐标系中,点 P 的坐标为 ( )
A.(3,-2) B.(-2,3)
C.(-3,2) D.(2,-3)
2.点 P(3,一5)到x轴、y轴的距离分别为 ( )
A.3,5 B.3,-5 C.5,3 D.-5,3
3.如图,已知,OB=2,三角形ABC三个顶点坐标分别是:A( ),C( ),B( ).
4.原点O的坐标是( , ),横轴上的点的坐 标为 (x, ),纵 轴上 的点 的 坐 标为( ,y).
5.已知点 P(3,a),并且P点到x轴的距离是2个单位长度,则 P 点的坐标为 .
6.点A在x 轴上,距离原点4个单位长度,则A点的坐标是 .
7.如图,根据坐标平面内点的位置,写出图中各点的坐标(坐标取整数).
8.如图,若点 D,E,F的坐标分别为(2,—2),(—2,-3),(4,3),请在图中标出来.
B 组
9.如图,在所给坐标系中描出下列各点的位置:A(-4,4);B(-2,2);C(3,-3);D(5,-5);E(-3,3);F(0,0).
你发现这些点有什么关系
你能再写出一些类似的点吗
10.已知O(0,0),B(1,2),点A在坐标轴上,且三角形OAB的面积为 2,求点 A的坐标.
C组
11.在平面直角坐标系中,一蚂蚁从原点 O 出发按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示.
(1)填写下列各点的坐标:
A ( ),A ( ),A ( );
(2)写出点 A 的坐标(n是正整数);
(3)指出蚂蚁从点 A 到点 A 的移动方向.
第3课时 平面直角坐标系(2) 点的坐标特征
基础知识夯实
知识沉淀
1.象限点的特征:
第一象限 第二象限 第三象限 第四象限 x轴 y轴
(+,+) (一,+) (一,一) (+,一) (x,0) (0,y)
(1)坐标平面分为4个象限和两条坐标轴(如图).
(2)注意:x轴、y轴不属于任何象限.
2.与坐标轴平行直线上点的特征:
(1)B(— 2,3),C(—2,—3),发现线段 BC 与 轴平行;
(2)C(—2,—3),D(1,—3),发现线段 CD 与 轴平行.
结论:(1)点 A,B的横坐标相同 AB∥ 轴;(2)点A,B的纵坐标相同 AB∥ 轴.
基础过关
1.已知点 A(2,5),B(4,—2),C(—2,3),D(—4,0),E(-3,-4),F(0,4),则:
(1)在第一象限的点是 ;
(2)在第二象限的点是 ;
(3)在第三象限的点是 ;
(4)在第四象限的点是 ;
(5)在x轴上的点是 ;
(6)在y轴上的点是 .
2.若点M(4,一2),点 N(4,5),则直线MN 与 轴平行.
3.已知点 A(-3,2),点 B(3,2),连接A,B 两点所成线段与 轴平行.
典型案例探究
知识点 1判断点所在象限
【例题1】请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上.
A(-5,2);B(3,-2);C(0,4);D(-6,0);E(1,8);F(0.0);G(5,0);H(-6,-4);I(0,-3).
【变式1】(1)点 P(一1,2)在平面直角坐标系中所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
(2)已知点 P 在第四象限,且到x轴的距离是2,到y轴的距离是3,则点 P 的坐标是 .
知识点 2 根据点的位置确定参数的值
【例题2】(1)点P(m+3,m+1)在平面直角坐标系的x轴上,则 m= ,点 P 坐标为 ;
(2)点P(m+3,m+1)在平面直角坐标系的 y轴上,则点 P 坐标为 ;
(3)若点(a,b--1)在第二象限,则a的取值范围是 ,b的取值范围是 .
【变式2】(1)已知点 P(2-a,3a+6)到两坐标轴的距离相等,则 P 点坐标为 ( )
A. (3,3) B. (6,-6)
C. (3,3)或(6,—6) D. (3,-3)
(2)平面直角坐标系中,若点A(a,b)在第三象限内,则点 B(a,一b)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
课后作业
A 组
1.点 P(--1,4)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.若点 P 在第二象限,且 P到x 轴的距离为3,到y的距离为4,则 P 点坐标为 ( )
A.(-3,-4) B.(-4,3)
C.(3,-4) D.(4,-3)
3.在平面直角坐标系中,有一点 P(a,b),已知ab=0,则 P点位置在 ( )
A. x轴上 B. y轴上
C.原点位置 D. x轴或y轴上
4.如果点A(m,n)在第一象限,那么点 B(-n,-m)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.在平面直角坐标系中,点( 一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
6.如果点 M(3,x)在第一象限,则x 的取值范围是
7.若点 M(a+5,a--2)在 x 轴上,则 a 的值为 ,此时点M到y轴的距离为 .
8.在平面直角坐标系中,已知点P(a,b)且ab<0,则点P 在第 象限.
B 组
9.若第二象限内的点 P(x,y)满足 则点 P 的坐标是 .
10.已知线段 MN=4,MN∥y 轴,若点 M 坐标为(一1,2),则点 N 坐标为 .
11.已知 P(1,4),点 A 在坐标轴上,S△NOp=4,则 A 点 坐标是 .
C 组
12.如图,正方形 A A A A ,正方形A A A A ,正方形A A A A ,…(每个正方形从第三象限的顶点开始,按顺时针方向,依次记为A ,A ,A ,A ;A ,A ,A ,A ;A ,A ,A ,A ;…)的中心均为坐标原点O,各边均与x轴或y 轴平行,若它们的边长依次是2,4,6,…,则顶点 A 的坐标为 .
第 1 课时 有序数对
【基础知识夯实】
知识沉淀
顺序
基础过关
(5,4) (1,8) (7,3) (6,6)
【典型案例探究】
例题1 (1)①(4,3) ②(6,6) ③(9,6) (2)羊 蛇
变式1 (1)①(2,6) ②(8,3) (2)北京
例题2 H
变式2 (3,6)
【课后作业】
1. D 2.(2.1) 3.(2.5) (4,4) (6,3) (2.3)
4.(2,3) (7,0)5. STUDY(学习)
6.排
7.解:相距3个格,两人经过的路径如图所示.
8.(1)放置 2个胡萝卜,2 棵青菜. (2)③ ①
9.共有 6 条路径,写出路径略.
第 2 课时 平面直角坐标系(1)——点的坐标
【基础知识夯实】
知识沉淀
1.(1)横轴 右 纵轴 上 (2)横坐标 纵坐标 坐标2.(-3,-4) -3 -4 (-4,1)
3.|x|
基础过关
1.(-4,1) 2. A(1,1),B(4,3),C(-3,2)
3.(1)5 4 (2)D
【典型案例探究】
例题1 (-2,4) (3,3) (0,-2) (2,5) (-3,0)
(2,0) (3,-2)
变式1 解:A(3.2). B(-3.-2),C(0,2),
D(0,-4),E(2,-1),F(-2,1).
【课后作业】
1. A 2. C 3.—2,3 2,0 —1,—1
4.0 0 0 0
5.(3,2)或(3,-2)解析:由一个点到x轴的距离是该点纵坐标的绝对值,所以a的绝对值等于2,这样a的值应等于±2.
6.(4,0)或(-4,0)
7.解:A(2,0). B(1,-1),C(0,0),D(1,1),E(2,2),F(-1,0),G(-1,1).
8.
9.略
10.(2,0),(-2,0),(0,4),(0,-4)
11.(1)2,0 4,0 6,0 (2)A (2n,0) (3)向上
第3课时 平面直角坐标系(2)———点的坐标特征【基础知识夯实】
知识沉淀
2. y x y x
基础过关
1.(1)A (2)C (3)E (4)B (5)D (6)F
2. y 3. x
【典型案例探究】
例题1 解:A在第二象限,B 在第四象限,C 在y轴的正半轴,D 在x 轴的负半轴,E在第一象限,F 在原点,G在x轴的正半轴,H 在第三象限,I 在 y 轴的负半轴.
变式1 (1)B (2)(3,-2)
例题2 (1)-1 (2,0) (2)(0,-2) (3)a<0 b>1
变式2 (1)C (2)B
【课后作业】
1. B 2. B 3. D 4. C 5. B
6. x>0 7.2 7 8.二或四 9.(-3,5)
10.(-1.6)或(-1,-2)
11.(2,0),(-2,0),(0,8),(0,-8)
12.(一505,505)
7.1 平面直角坐标系
第1课时 有序数对
基础知识夯实
中小学教育资源及组卷应用平台
知识沉淀
有序数对:有 的两个数a与b组成的数对,叫做有序数对,记作(a,b).
注:利用有序数对,可以准确地表示出一个位置.
基础过关
如图,小鸡的位置可以用有序数对(2,3)表示,请说出图中其他物体位置.
苹果: ;足球: ;
花朵: ;香蕉: .
典型案例探究
知识点 1 根据位置写出有序数对
【例题1】图中的十二生肖都可以用有序数对表示,比如鸡用(2,8)表示.
(1)请表示出以下生肖的位置.
①牛: ;②龙: ;③马: .
(2)(7,2)表示 的位置;
(8,7)表示 的位置.
【变式1】写出如下“地图”上各城市对应的有序数对(经度在前,纬度在后),如南京用(7,4)表示.
(1)表示下列地点的位置.
①银川: ;②上海: .
(2)(6,7)表示 的位置.
知识点 2 根据有序数对确定位置
【例题2】如图,若P 为(1,2),B 为(2,5),进行“找宝”游戏,如果宝藏藏在(3,4)字母牌的下面,那么应该在字母 的下面.
【变式2】如图是某校的平面示意图,如果用(9,3)表示图中图书馆的位置,那么实验楼的位置可表示为
课后作业
A 组
1.如果一张“13排10号”的电影票简记为(13,10),那么(10,13)表示的电影票是 ( )
A.10行13列 B.13 行 10列
C.13排 10 号 D.10 排13号
2.如图是小刚画的一张脸,如果用(1,3)表示左眼,用(3,3)表示右 眼,那么 嘴 的 位 置 可 以 表 示 成
3.如图,如果点 A 的位置为(3,2),那么点 B的位置为 ,点 C 的位置为 ,点 D 和点 E 的位置分别为 , .
4.如图,(5,2)表示炮的位置,用(4,0)表示帅的位置,则兵的位置可表示为 ,马的位置可表示为
5.有一个英文单词的字母顺序对应图中的有序数对,分别为(5,3),(6,3),(7,3),(4,1),(4,4),请你把这个英文单词写出来或者翻译成中文: .
B 组
6.如图,(1,3)表示第一列第三排,请用彩笔把以下位置的五角星涂上颜色.
(4,6);(3,4);(5,4);(2,2);(4,2);(6,2).
7.如图,A 的位置为(2,6),小明从 A 出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格 请分别画出他们经过的路径.
8.如图,若点A(2,1)表示放置2 个胡萝卜,1 棵青菜;点 B(4,2)表示放置4个胡萝卜,2 棵青菜.
(1)请写出点C所表示的意义;
(2)若一只小兔子从 A到达B(顺着方格线走)有以下几种路径可选择:
①A→C→D→B;②A→E→D→B;③A→E→F→B.则走哪条路径吃到胡萝卜最多 走哪条路径吃到青菜最多
C 组
9.如图,点 A 表示3 街与 5 大道的十字路口,点 B表示 5 街与 3 大道的十字路口,如果用(3,5)→(4,5)→(5,5)→(5,4)→(5,3)表示由 A到B 的一条路径,那么从A到B 共有几条路径(只能向右或向下走) 请写出其中1条路径.
第 2 课时 平面直角坐标系(1)——点的坐标
基础知识夯实
知识沉淀
1.平面直角坐标系:
(1)在平面内,由两条互相垂直、原点重合的数轴组成平面直角坐标系,其中水平的数轴称为x 轴或 ,习惯上取向 为正方向;竖直的数轴称为y轴或 ,取向 为正方向;两坐标轴的交点为平面直角坐标系的原点.
(2)对于平面内任意一点 P,过点 P 分别向x 轴、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点 P 的 、 ,有序数对(a,b)叫做点 P 的 .
2.如图,填空:
点 B的坐标为 ,其中横坐标为 ,纵坐标为 ;点C的坐标为 .
3.点(x,y)到x 轴的距离是|y|,到 y 轴的距离是 ·
基础过关
1.点C的横坐标是-4,纵坐标是1,则点 C 的坐标记作 .
2.如图,请写出点 A,B,C的坐标: .
3.(1)P点的坐标为(—4,—5),则点 P 到x 轴的距离为 ,点 P 到y 轴的距离为 .
(2)点A(3,—4)到x轴的距离是 ( )
A.-4 B.3 C.5 D.4
典型案例探究
知识点 1 根据点的位置写出坐标
【例题1】如图,写出下列各点的坐标:
A点( —1 , —1 ),
B点 ,C点 ,
D点 ,E点 ,
F点 ,G点 ,
H 点 .
知识点 2 根据坐标确定点的位置
【例题2】在如图所示的平面直角坐标系中描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(3,-2),E(0,-4),F(-2,0),G(4,0),H(0,3).
【变式1】如图,写出下列各点坐标.
【变式2】在如图所示的平面直角坐标系中描出下列各点:
A(2,3),B(-2,3),C(3,-5),
D(-4,-5),E(0,-3),F(5,0),
课后作业
A 组
1.如图,在平面直角坐标系中,点 P 的坐标为 ( )
A.(3,-2) B.(-2,3)
C.(-3,2) D.(2,-3)
2.点 P(3,一5)到x轴、y轴的距离分别为 ( )
A.3,5 B.3,-5 C.5,3 D.-5,3
3.如图,已知,OB=2,三角形ABC三个顶点坐标分别是:A( ),C( ),B( ).
4.原点O的坐标是( , ),横轴上的点的坐 标为 (x, ),纵 轴上 的点 的 坐 标为( ,y).
5.已知点 P(3,a),并且P点到x轴的距离是2个单位长度,则 P 点的坐标为 .
6.点A在x 轴上,距离原点4个单位长度,则A点的坐标是 .
7.如图,根据坐标平面内点的位置,写出图中各点的坐标(坐标取整数).
8.如图,若点 D,E,F的坐标分别为(2,—2),(—2,-3),(4,3),请在图中标出来.
B 组
9.如图,在所给坐标系中描出下列各点的位置:A(-4,4);B(-2,2);C(3,-3);D(5,-5);E(-3,3);F(0,0).
你发现这些点有什么关系
你能再写出一些类似的点吗
10.已知O(0,0),B(1,2),点A在坐标轴上,且三角形OAB的面积为 2,求点 A的坐标.
C组
11.在平面直角坐标系中,一蚂蚁从原点 O 出发按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位长度,其行走路线如图所示.
(1)填写下列各点的坐标:
A ( ),A ( ),A ( );
(2)写出点 A 的坐标(n是正整数);
(3)指出蚂蚁从点 A 到点 A 的移动方向.
第3课时 平面直角坐标系(2) 点的坐标特征
基础知识夯实
知识沉淀
1.象限点的特征:
第一象限 第二象限 第三象限 第四象限 x轴 y轴
(+,+) (一,+) (一,一) (+,一) (x,0) (0,y)
(1)坐标平面分为4个象限和两条坐标轴(如图).
(2)注意:x轴、y轴不属于任何象限.
2.与坐标轴平行直线上点的特征:
(1)B(— 2,3),C(—2,—3),发现线段 BC 与 轴平行;
(2)C(—2,—3),D(1,—3),发现线段 CD 与 轴平行.
结论:(1)点 A,B的横坐标相同 AB∥ 轴;(2)点A,B的纵坐标相同 AB∥ 轴.
基础过关
1.已知点 A(2,5),B(4,—2),C(—2,3),D(—4,0),E(-3,-4),F(0,4),则:
(1)在第一象限的点是 ;
(2)在第二象限的点是 ;
(3)在第三象限的点是 ;
(4)在第四象限的点是 ;
(5)在x轴上的点是 ;
(6)在y轴上的点是 .
2.若点M(4,一2),点 N(4,5),则直线MN 与 轴平行.
3.已知点 A(-3,2),点 B(3,2),连接A,B 两点所成线段与 轴平行.
典型案例探究
知识点 1判断点所在象限
【例题1】请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上.
A(-5,2);B(3,-2);C(0,4);D(-6,0);E(1,8);F(0.0);G(5,0);H(-6,-4);I(0,-3).
【变式1】(1)点 P(一1,2)在平面直角坐标系中所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
(2)已知点 P 在第四象限,且到x轴的距离是2,到y轴的距离是3,则点 P 的坐标是 .
知识点 2 根据点的位置确定参数的值
【例题2】(1)点P(m+3,m+1)在平面直角坐标系的x轴上,则 m= ,点 P 坐标为 ;
(2)点P(m+3,m+1)在平面直角坐标系的 y轴上,则点 P 坐标为 ;
(3)若点(a,b--1)在第二象限,则a的取值范围是 ,b的取值范围是 .
【变式2】(1)已知点 P(2-a,3a+6)到两坐标轴的距离相等,则 P 点坐标为 ( )
A. (3,3) B. (6,-6)
C. (3,3)或(6,—6) D. (3,-3)
(2)平面直角坐标系中,若点A(a,b)在第三象限内,则点 B(a,一b)所在的象限是 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
课后作业
A 组
1.点 P(--1,4)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
2.若点 P 在第二象限,且 P到x 轴的距离为3,到y的距离为4,则 P 点坐标为 ( )
A.(-3,-4) B.(-4,3)
C.(3,-4) D.(4,-3)
3.在平面直角坐标系中,有一点 P(a,b),已知ab=0,则 P点位置在 ( )
A. x轴上 B. y轴上
C.原点位置 D. x轴或y轴上
4.如果点A(m,n)在第一象限,那么点 B(-n,-m)在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
5.在平面直角坐标系中,点( 一定在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
6.如果点 M(3,x)在第一象限,则x 的取值范围是
7.若点 M(a+5,a--2)在 x 轴上,则 a 的值为 ,此时点M到y轴的距离为 .
8.在平面直角坐标系中,已知点P(a,b)且ab<0,则点P 在第 象限.
B 组
9.若第二象限内的点 P(x,y)满足 则点 P 的坐标是 .
10.已知线段 MN=4,MN∥y 轴,若点 M 坐标为(一1,2),则点 N 坐标为 .
11.已知 P(1,4),点 A 在坐标轴上,S△NOp=4,则 A 点 坐标是 .
C 组
12.如图,正方形 A A A A ,正方形A A A A ,正方形A A A A ,…(每个正方形从第三象限的顶点开始,按顺时针方向,依次记为A ,A ,A ,A ;A ,A ,A ,A ;A ,A ,A ,A ;…)的中心均为坐标原点O,各边均与x轴或y 轴平行,若它们的边长依次是2,4,6,…,则顶点 A 的坐标为 .
第 1 课时 有序数对
【基础知识夯实】
知识沉淀
顺序
基础过关
(5,4) (1,8) (7,3) (6,6)
【典型案例探究】
例题1 (1)①(4,3) ②(6,6) ③(9,6) (2)羊 蛇
变式1 (1)①(2,6) ②(8,3) (2)北京
例题2 H
变式2 (3,6)
【课后作业】
1. D 2.(2.1) 3.(2.5) (4,4) (6,3) (2.3)
4.(2,3) (7,0)5. STUDY(学习)
6.排
7.解:相距3个格,两人经过的路径如图所示.
8.(1)放置 2个胡萝卜,2 棵青菜. (2)③ ①
9.共有 6 条路径,写出路径略.
第 2 课时 平面直角坐标系(1)——点的坐标
【基础知识夯实】
知识沉淀
1.(1)横轴 右 纵轴 上 (2)横坐标 纵坐标 坐标2.(-3,-4) -3 -4 (-4,1)
3.|x|
基础过关
1.(-4,1) 2. A(1,1),B(4,3),C(-3,2)
3.(1)5 4 (2)D
【典型案例探究】
例题1 (-2,4) (3,3) (0,-2) (2,5) (-3,0)
(2,0) (3,-2)
变式1 解:A(3.2). B(-3.-2),C(0,2),
D(0,-4),E(2,-1),F(-2,1).
【课后作业】
1. A 2. C 3.—2,3 2,0 —1,—1
4.0 0 0 0
5.(3,2)或(3,-2)解析:由一个点到x轴的距离是该点纵坐标的绝对值,所以a的绝对值等于2,这样a的值应等于±2.
6.(4,0)或(-4,0)
7.解:A(2,0). B(1,-1),C(0,0),D(1,1),E(2,2),F(-1,0),G(-1,1).
8.
9.略
10.(2,0),(-2,0),(0,4),(0,-4)
11.(1)2,0 4,0 6,0 (2)A (2n,0) (3)向上
第3课时 平面直角坐标系(2)———点的坐标特征【基础知识夯实】
知识沉淀
2. y x y x
基础过关
1.(1)A (2)C (3)E (4)B (5)D (6)F
2. y 3. x
【典型案例探究】
例题1 解:A在第二象限,B 在第四象限,C 在y轴的正半轴,D 在x 轴的负半轴,E在第一象限,F 在原点,G在x轴的正半轴,H 在第三象限,I 在 y 轴的负半轴.
变式1 (1)B (2)(3,-2)
例题2 (1)-1 (2,0) (2)(0,-2) (3)a<0 b>1
变式2 (1)C (2)B
【课后作业】
1. B 2. B 3. D 4. C 5. B
6. x>0 7.2 7 8.二或四 9.(-3,5)
10.(-1.6)或(-1,-2)
11.(2,0),(-2,0),(0,8),(0,-8)
12.(一505,505)
