小升初高频考点检测卷(试题)2023-2024学年数学六年级下册北师大版(含答案)
文档属性
| 名称 | 小升初高频考点检测卷(试题)2023-2024学年数学六年级下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 538.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-29 08:50:05 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
小升初高频考点检测卷(试题)2023-2024学年数学六年级下册北师大版
一、选择题
1.m,n是两种相关联的量(m,n均不为0),下列各式中,m和n成反比例的是( )。
A. B. C. D.
2.李叔叔要给房子的四面涂上颜色,但不管怎么设计,总是至少有两面墙是同一种颜色,李叔叔可能买了( )种不同颜色的涂料。
A.3 B.4 C.5 D.6
3.一件上衣售价96元,先提价,又降价,这时这件衣服的售价是( )元。
A.160 B.120 C.90 D.60
4.用长20cm、宽15cm、高6cm的长方体木块堆成一个正方体,至少需要( )块这样的长方体木块。
A.30 B.60 C.90 D.120
5.学校原有足球和篮球共36个,其中足球与篮球的数量比是7∶2,又买来一些足球后,足球占总数的80%,现在学校足球和篮球共有( )个。
A.42 B.40 C.45 D.48
二、填空题
6.2.05时=( )时( )分 5吨28千克=( )吨
7.比100米少25%是( )米,比8千克多千克是( )千克。
8.如果,那么x∶y=( )∶( )。
9.一件商品原价2000元,现打七五折销售,比原来便宜( )元。
10.下图是一个蛋糕盒,盒子上扎了一根漂亮的丝带,已知蛋糕底面周长是94.2cm,高是18cm,接头处用去了30cm,这根丝带长( )cm。
11.一个长方形的周长是60cm,长和宽的比是3∶2,这个长方形的长是( )cm,面积是( )cm2。
12.一种药水是用药粉和水按1∶200配制成的,现有药粉12千克,需要加水( )千克,配制成了药水是( )千克。
13.将一个棱长是4dm的正方体容器装满水后,如果倒入一个底面积是8dm2的圆柱形容器正好装满,这个圆柱的高是( )dm,如果倒入底面积是8dm2的圆锥形容器,正好装满,这个圆锥形的高是( )dm。
三、判断题
14.甲市15℃,乙市﹣20℃,丙市﹣6℃,这三个城市中乙市的气温最低。( )
15.一幅图的比例尺是1∶30000,则图上的1厘米表示实际距离300米。( )
16.圆柱的底面周长扩大到原来的2倍,高缩小到原来的,体积不变。( )
17.一个长方形的长增加20%,宽减少20%,其面积不变。( )
18.甲、乙、丙三数之比为4∶7∶10,这三个数的平均数是35,最小的数是25。( )
四、计算题
19.直接写出得数。
20.计算下面各题。(怎样简便怎样算)
21.解比例。
(1) (2) (3)
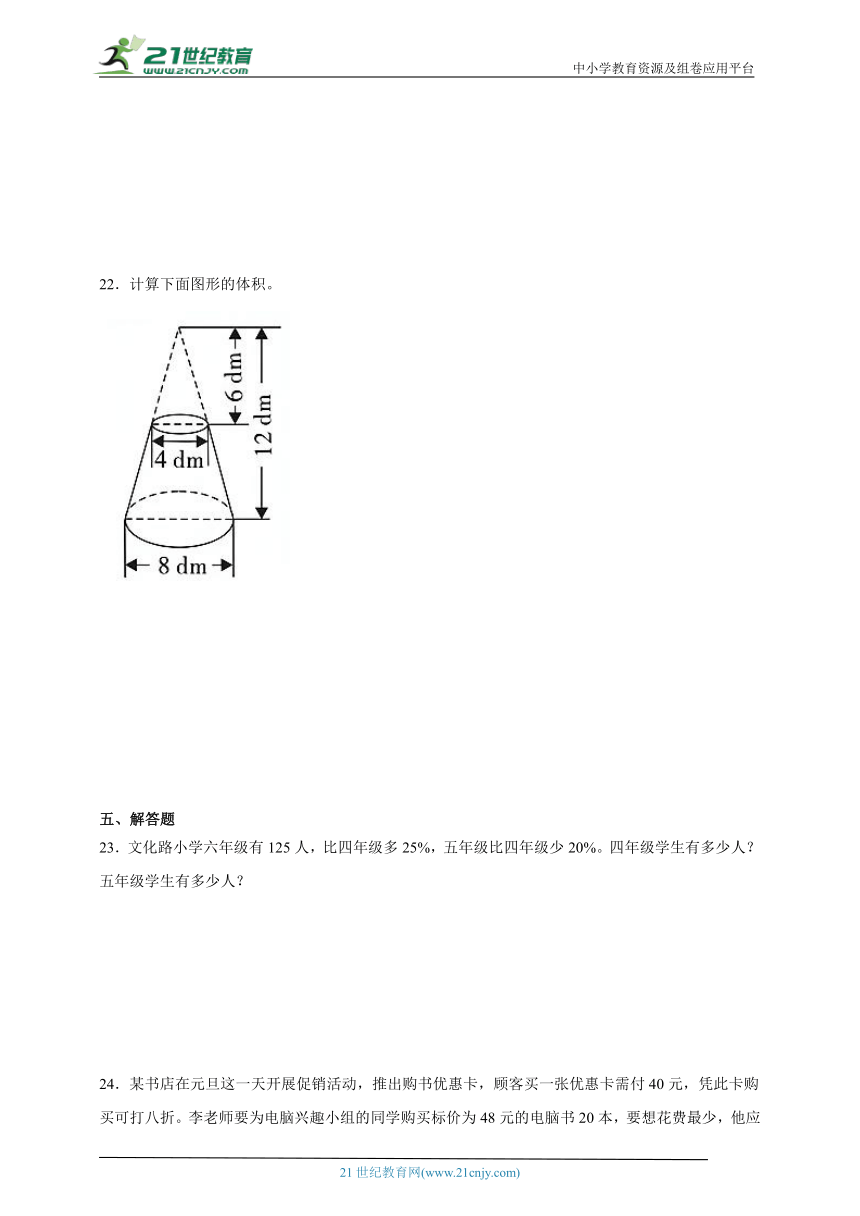
22.计算下面图形的体积。
五、解答题
23.文化路小学六年级有125人,比四年级多25%,五年级比四年级少20%。四年级学生有多少人?五年级学生有多少人?
24.某书店在元旦这一天开展促销活动,推出购书优惠卡,顾客买一张优惠卡需付40元,凭此卡购买可打八折。李老师要为电脑兴趣小组的同学购买标价为48元的电脑书20本,要想花费最少,他应该选择优惠卡购买,还是原价购买?请计算说明。
25.一台压路机的滚筒是圆柱形,滚筒的宽是2米,横截面半径是0.5米,滚筒每分滚动10周,滚筒一分压过的路面是多少平方米?
26.2022年第24届冬季奥运会在北京和张家口举办,在一幅比例尺是1∶300000的冬奥会宣传图上,京张高铁全线长58厘米,京张高铁实际全线长多少千米?
27.学校在端午节来临之际,组织学生进行包棕子比赛,四、五、六年级代表队完成粽子的个数比为4∶5∶6,已知四年级代表队包了60个棕子,三个代表队一共包了多少个棕子?
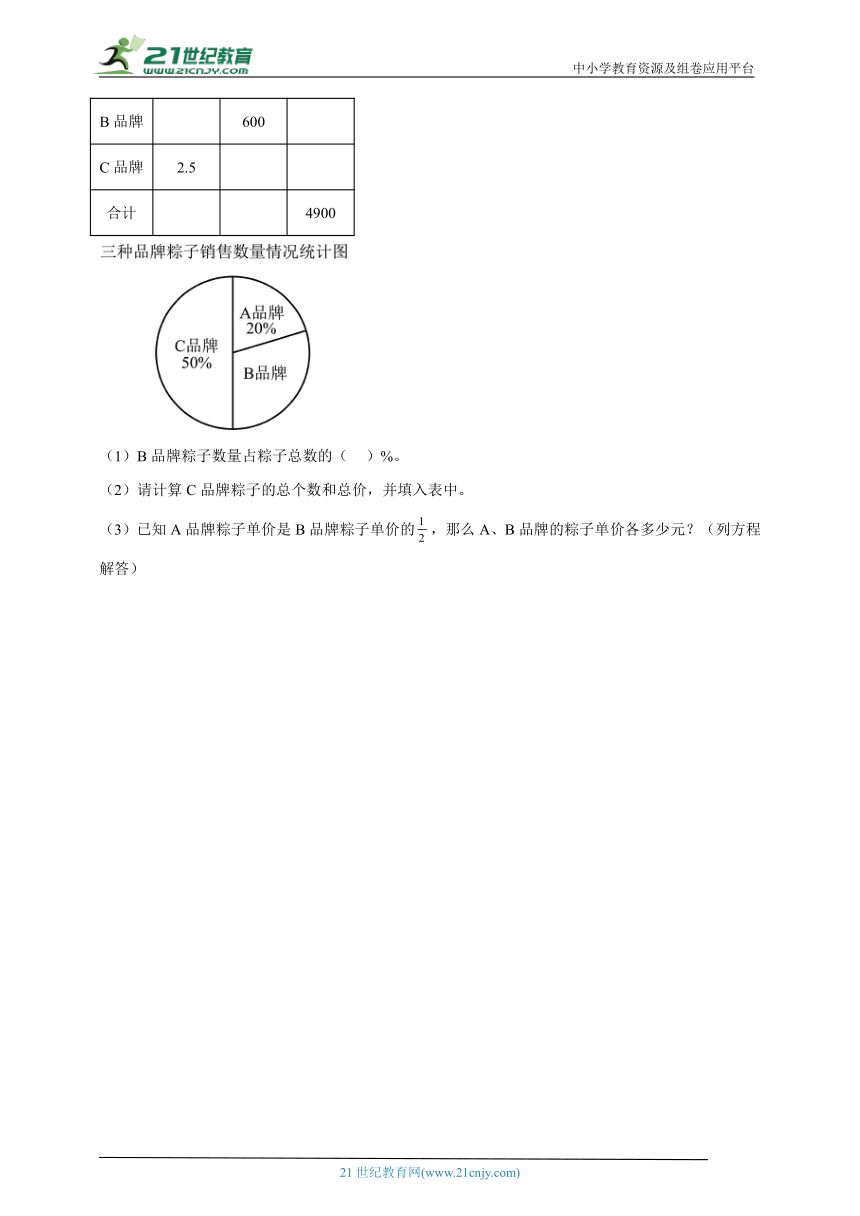
28.端午节是中国四大传统节日之一,端午文化在世界上影响广泛,吃粽子是端午节的一项重要习俗。下面图表是某超市端午节当天所销售粽子的一些信息,请根据图表中信息解答下面的问题。
单价/元 数量/个 总价/元
A品牌 400
B品牌 600
C品牌 2.5
合计 4900
(1)B品牌粽子数量占粽子总数的( )%。
(2)请计算C品牌粽子的总个数和总价,并填入表中。
(3)已知A品牌粽子单价是B品牌粽子单价的,那么A、B品牌的粽子单价各多少元?(列方程解答)
参考答案:
1.D
【分析】两种相关联的量,若它们的比值一定,两种量成正比例关系;若它们的乘积一定,两种量成反比例关系。
【详解】A.m和n的比值一定,m和n成正比例关系。
B.根据=m,得=2,比值一定,m和n成正比例关系。
C.根据=,得=,比值一定,m和n成正比例关系。
D.根据=8,得mn=,乘积一定,m和n成反比例关系。
故答案为:D
【点睛】辨识两种量成正比例还是成反比例,就看两种量的比值一定还是乘积一定。
2.A
【分析】本题可以用抽屉原理的最不利原则;故意在3个墙面上涂上甲、乙、丙3种颜色,没有重复,但第4面墙只能选甲、乙、丙中的一种,至少有两面的颜色是一致的;所以得出颜料的种数是3种。
【详解】4-1=3(种)
故答案为:A
【点睛】此题属于抽屉原理的习题,做题时应确定哪个是抽屉,哪个相当于物体个数,然后可利用抽屉原理的最不利原则进行分析即可。
3.C
【分析】根据题意,把上衣原价看作单位“1”,则涨降价后的价格=原价×(1+),求出涨价后的价格后,把这个价格看作单位“1”,现在的价格=涨价后的价格×(1-),求出即可。
【详解】96×(1+)
=96×
=24×5
=120(元)
120×(1-)
=120×
=90(元)
故答案为:C
【点睛】此题答题的关键是分清前后两个单位“1”的区别,再由此列出数量关系解答。
4.D
【分析】首先要求出堆成的正方体的棱长是多少厘米,也就是要求出20、15、6的最小公倍数,这个数就是堆成的正方体的棱长;再分别用棱长除以原来的长、宽、高,求出长要堆几块,宽要堆几块,高要堆几块,最后用这三个块数相乘就得到需要的总块数。
【详解】20、15和6的最小公倍数是60
60÷20=3(块)
60÷15=4(块)
60÷6=10(块)
3×4×10=120(块)
故答案为:D
【点睛】此题主要考查正方体的特征,以及最小公倍数的应用。
5.B
【分析】足球与篮球的数量比是7∶2,则篮球占总数的,则可以据此算出篮球的个数。
又买进一些足球后,足球占总数的80%,则篮球占总数的1-80%=20%,用篮球的数量可以算出足球和篮球的总数。
【详解】36×=8(个)
8÷(1-80%)
=8÷20%
=40(个)
故答案为:A
【点睛】解答此题的关键是找到不变的量,即前后没有变化的是篮球的个数。再根据篮球所占总数的百分比可以求出答案。
6. 2 3 5.028
【分析】根据1时=60分,1吨=1000千克,进行换算即可。
【详解】0.05×60=3(分),2.05时=2时3分;28÷1000=0.028(吨),5吨28千克=5.028吨
【点睛】单位大变小乘进率,单位小变大除以进率。
7. 75
【分析】求比100米少25%的数是多少,用100-100×25%即可解答;求比8千克多千克是多少,用加法解答即可。
【详解】100-100×25%
=100-25
=75(米)
8+=(千克)
【点睛】本题考查求比一个数少百分之几的数是多少,明确单位“1”是解题的关键。
8. 8 5
【分析】根据比例的基本性质可知,两内项之积等于两外项之积,可得5x=8y,把5和x看作比例的两个外项,把8和y看作比例的两个内项,即可写出比例式。
【详解】根据分析得,如果,5x=8y,
可写成比例式:x∶y=8∶5。
【点睛】此题的解题关键是灵活运用比例的基本性质求解。
9.500
【分析】将原价看作单位“1”,打七五折销售,现价是原价的75%,比原来便宜了1-75%,原价×便宜的对应百分率=便宜的钱数,据此分析。
【详解】2000×(1-75%)
=2000×0.25
=500(元)
【点睛】关键是理解折扣的意义,几折就是百分之几十。
10.414
【分析】由题意可知,根据圆的周长公式:C=πd,据此可求出底面圆的直径,这根丝带的长度=8条直径的长度+8条高的长度+接头处的长度,据此解答即可。
【详解】94.2÷3.14=30(cm)
30×8+8×18+30
=240+144+30
=384+30
=414(cm)
【点睛】本题考查圆的周长,明确彩带都是由哪几部分构成的是解题的关键。
11. 18 216
【分析】根据长方形的周长=(长+宽)×2,可得长+宽=60÷2=30(cm),已知长和宽的比是3∶2,长可看作3份,宽看作2份,长和宽共占(3+2)份,可求出长占长和宽总长的,利用求一个数的几分之几是多少的计算方法,用30×求出长方形的长,继而求出长方形的宽,再利用长方形的面积公式,代入数据即可得解。
【详解】60÷2=30(cm)
30×=30×=18(cm)
30-18=12(cm)
18×12=216(cm2)
【点睛】此题主要考查按比例分配的应用题的解答方法,利用长方形的周长和面积公式,解决实际的问题。
12. 2400 2412
【分析】药粉和水的比是1∶200,即水的质量是药粉的200倍,所以用药粉乘200求出需要加的水,再用水加药粉就等于药水。
【详解】12×200=2400(千克)
2400+12=2412(千克)
【点睛】本题考查了比的问题,关键是根据比的意义先求出水的质量。
13. 8 24
【分析】根据正方体的体积公式:V=a3,求出水的体积,然后根据圆柱的体积公式:V=Sh,据此可求出圆柱形容器的高;再根据圆锥的体积公式:V=Sh,据此求出圆锥形容器的高。
【详解】4×4×4÷8
=16×4÷8
=64÷8
=8(dm)
4×4×4×3÷8
=64×3÷8
=192÷8
=24(dm)
【点睛】本题考查圆柱和圆锥的体积,熟记公式是解题的关键。
14.√
【分析】要比较这几个城市的气温高低,就要比较这几个城市气温的数值的大小。在数轴上,从左到右的顺序,就是数从小到大的顺序。这几个数值在数轴上从左到右依次是:﹣20、﹣6、15,据此解答。
【详解】因为﹣20<﹣6<15,即在数轴上,﹣20位于最左边,因为越往左,数越小,所以乙市的气温最低。原题说法正确。
故答案为:√
【点睛】本题主要考查正、负数的大小比较,要求学生熟练掌握。
15.√
【分析】根据实际距离=图上距离÷比例尺,再结合已知比例尺:1∶30000,求出当图上长度为1厘米的实际长度,然后跟题中结果对比即可。
【详解】1÷=30000(厘米)
30000厘米=300米
所以图上1厘米表示实际300米;
故答案为:√
【点睛】本题主要考查比例尺的意义,熟练掌握比例尺的意义并灵活运用。
16.√
【分析】假设原来圆柱的底面周长为6.28,高为8,则变化后圆柱的底面周长为(6.28×2),高为(8×),根据圆的周长公式:C=2πr,圆柱的体积公式:V=πr2h,据此求出圆柱变化前后的体积,再进行对比即可。
【详解】假设原来圆柱的底面周长为6.28,高为8
6.28÷3.14÷2
=2÷2
=1
3.14×12×8
=3.14×1×8
=3.14×8
=25.12
变化后圆柱的底面周长为:6.28×2=12.56
高为8×=2
12.56÷3.14÷2
=4÷2
=2
3.14×22×2
=3.14×4×2
=12.56×2
=25.12
则圆柱的底面周长扩大到原来的2倍,高缩小到原来的,体积不变。说法正确。
故答案为:√
【点睛】本题考查圆柱的体积,熟记公式是解题的关键。
17.×
【分析】设长方形的长和宽分别是a和b,那么原来的面积为ab,现在的面积为(1+20%)a×(1-20%)b,即0.96ab,进行比较即可解答。
【详解】设长方形的长为a,宽为b。
原来面积:
a×b=ab
现在面积:
(1+20%)a×(1-20%)b
=1.2a×0.8b
=0.96ab
ab>0.96ab
故答案为:×
【点睛】解答本题的关键是求出长方形变化前后的面积,进而进行判断。
18.×
【分析】平均数×个数=总数,总数÷总份数=一份数,一份数×最小数对应份数=最小的数,据此分析。
【详解】35×3÷(4+7+10)×4
=105÷21×4
=20
最小的数是20。
故答案为:×
【点睛】关键是理解平均数和比的意义。
19.1.25;;2;0;
;;0.72;
【详解】略
20.12;16
1;3.15
【分析】根据乘法分配律将原式转化成(54+41+1)×进行简算;
根据乘法分配律将原式转化成×(101-1)进行简算;
先算小括号里的加法,再算小括号外中括号里的减法,最后算中括号外的除法;
先算3.75×10%结果为0.375,将其转化成分数为,根据减法的性质,将原式转化成4.15-(+),先算小括号里的加法,再算小括号外的减法即可。
【详解】
=×54+×41+×1
=(54+41+1)×
=96×
=12
=×101-×1
=×(101-1)
=×100
=16
=[2-(+)]÷
=[2-]÷
=÷
=×
=1
=4.15--
=4.15-(+)
=4.15-1
=3.15
21.(1);(2)x=9.6;(3)
【分析】
(1)根据比例的基本性质,把式子转化为,再化简方程,最后根据等式的性质,方程两边同时除以即可;
(2)根据比例的基本性质,把式子转化为5x=4×12,再化简方程,最后根据等式的性质,方程两边同时除以5即可;
(3)先化简比例,根据比例的基本性质,把式子转化为,再化简方程,最后根据等式的性质,方程两边同时除以即可。
【详解】
(1)
解:
(2)
解:5x=4×12
5x=48
5x÷5=48÷5
x=9.6
(3)
解:
22.175.84dm3
【分析】根据圆锥的体积公式,用底面直径为8dm,高为12dm的圆锥的体积减去底面直径为4dm,高为6dm的圆锥的体积,根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】×3.14×(8÷2)2×12-×3.14×(4÷2)2×6
=×3.14×16×12-×3.14×4×6
=200.96-25.12
=175.84(dm3)
23.100人;80人
【分析】将四年级人数看作单位“1”,六年级人数是四年级的(1+25%),六年级人数÷对应百分率=四年级人数;将四年级人数看作单位“1”,五年级人数是四年级的(1-20%),四年级人数×五年级对应百分率=五年级人数。
【详解】
(人)
(人)
答:四年级学生有100人,五年级学生有80人。
24.优惠卡购买;理由见详解
【分析】分别计算出按优惠卡购买需要支付的总价和按原价购买需要支付的总价,选择总价最少的方式购买花费最少。
原价购买:根据总价=单价×数量,代入相应数值计算;
优惠卡购买:打八折,即现价是原价的80%,先计算出以单价48元购买20本电脑书的总价钱,再用总价钱乘80%,所得结果再加上购买优惠卡40元,即为按优惠卡购买需付的钱数。
【详解】原价购买:48×20=960(元)
优惠卡购买:48×20×80%+40
=960×0.8+40
=768+40
=808(元)
因为808<960,所以按优惠卡购买需要支付的费用最少,因此选择按优惠卡购买。
25.62.8平方米
【分析】滚筒滚动一周的面积就是这个圆柱形的侧面积,利用圆柱的侧面积=圆柱的底面周长×宽=,即可求得一周压过的路面面积,每分钟转10周,即乘10即可。
【详解】
(平方米)
6.28×10=62.8(平方米)
答:滚筒一分压过的路面是62.8平方米。
【点睛】
26.174千米
【分析】本题根据实际距离=图上距离÷比例尺,代入数据计算即可,注意单位换算。
【详解】(厘米)
17400000厘米=174千米
答:京张高铁实际全线长174千米。
27.225个
【分析】由已知可得,四年级代表队完成粽子的份数为4,个数为60,可算出每份的个数为:60÷4=15(个),再算出三个年级代表队完成粽子的总份数为4+5+6=15,再用每份的个数乘总份数,即15×15=225(个),据此解答。
【详解】60÷4×(4+5+6)
=15×15
=225(个)
答:三个代表队一共包了225个棕子。
28.(1)30%
(2)1000个;2500元;见详解
(3)1.5元;3元
【分析】(1)把三个品牌的总数看作单位“1”,用单位“1”减去C品牌和A品牌所占总数的百分率,即可求出B品牌的百分率;
(2)已知A品牌的粽子销售400个,A品牌的粽子占总数的20%,已知一个数的百分比是多少求这个数,用除法计算,即用400除以20%,先算出三种品牌粽子的总数,再减去A品牌和B品牌粽子销售量的和,即可求出C品牌粽子销售量并填表,再根据总价=单价×数量,求出总价即可并填表即可。
(3)A品牌粽子单价是B品牌粽子单价的,设B品牌粽子单价为x,则A品牌粽子单价是x,再根A品牌粽子总价+B品牌粽子总价=三种品牌粽子的总价减去C品牌粽子总价;据此列方程解答即可。
【详解】(1)1-50%-20%
=50%-20%
=30%
即B品牌粽子数量占粽子总数的30%。
(2)400÷20%=2000(个)
2000-(600+400)
=2000-1000
=1000(个)
1000×2.5=2500(元)
答:C品牌粽子的总个数是1000个,总价是2500元;
填表如下:
单价/元 数量/个 总价/元
A品牌 400
B品牌 600
C品牌 2.5 1000 2500
合计 4900
(3)解:设B品牌粽子单价为x,则A品牌粽子单价是x;
600x+400×x=4900-2500
600x+200x=2400
800x=2400
800x÷800=2400÷800
x=3(元)
3×=1.5(元)
答:A品牌的粽子单价1.5元;B品牌的粽子单价3元。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初高频考点检测卷(试题)2023-2024学年数学六年级下册北师大版
一、选择题
1.m,n是两种相关联的量(m,n均不为0),下列各式中,m和n成反比例的是( )。
A. B. C. D.
2.李叔叔要给房子的四面涂上颜色,但不管怎么设计,总是至少有两面墙是同一种颜色,李叔叔可能买了( )种不同颜色的涂料。
A.3 B.4 C.5 D.6
3.一件上衣售价96元,先提价,又降价,这时这件衣服的售价是( )元。
A.160 B.120 C.90 D.60
4.用长20cm、宽15cm、高6cm的长方体木块堆成一个正方体,至少需要( )块这样的长方体木块。
A.30 B.60 C.90 D.120
5.学校原有足球和篮球共36个,其中足球与篮球的数量比是7∶2,又买来一些足球后,足球占总数的80%,现在学校足球和篮球共有( )个。
A.42 B.40 C.45 D.48
二、填空题
6.2.05时=( )时( )分 5吨28千克=( )吨
7.比100米少25%是( )米,比8千克多千克是( )千克。
8.如果,那么x∶y=( )∶( )。
9.一件商品原价2000元,现打七五折销售,比原来便宜( )元。
10.下图是一个蛋糕盒,盒子上扎了一根漂亮的丝带,已知蛋糕底面周长是94.2cm,高是18cm,接头处用去了30cm,这根丝带长( )cm。
11.一个长方形的周长是60cm,长和宽的比是3∶2,这个长方形的长是( )cm,面积是( )cm2。
12.一种药水是用药粉和水按1∶200配制成的,现有药粉12千克,需要加水( )千克,配制成了药水是( )千克。
13.将一个棱长是4dm的正方体容器装满水后,如果倒入一个底面积是8dm2的圆柱形容器正好装满,这个圆柱的高是( )dm,如果倒入底面积是8dm2的圆锥形容器,正好装满,这个圆锥形的高是( )dm。
三、判断题
14.甲市15℃,乙市﹣20℃,丙市﹣6℃,这三个城市中乙市的气温最低。( )
15.一幅图的比例尺是1∶30000,则图上的1厘米表示实际距离300米。( )
16.圆柱的底面周长扩大到原来的2倍,高缩小到原来的,体积不变。( )
17.一个长方形的长增加20%,宽减少20%,其面积不变。( )
18.甲、乙、丙三数之比为4∶7∶10,这三个数的平均数是35,最小的数是25。( )
四、计算题
19.直接写出得数。
20.计算下面各题。(怎样简便怎样算)
21.解比例。
(1) (2) (3)
22.计算下面图形的体积。
五、解答题
23.文化路小学六年级有125人,比四年级多25%,五年级比四年级少20%。四年级学生有多少人?五年级学生有多少人?
24.某书店在元旦这一天开展促销活动,推出购书优惠卡,顾客买一张优惠卡需付40元,凭此卡购买可打八折。李老师要为电脑兴趣小组的同学购买标价为48元的电脑书20本,要想花费最少,他应该选择优惠卡购买,还是原价购买?请计算说明。
25.一台压路机的滚筒是圆柱形,滚筒的宽是2米,横截面半径是0.5米,滚筒每分滚动10周,滚筒一分压过的路面是多少平方米?
26.2022年第24届冬季奥运会在北京和张家口举办,在一幅比例尺是1∶300000的冬奥会宣传图上,京张高铁全线长58厘米,京张高铁实际全线长多少千米?
27.学校在端午节来临之际,组织学生进行包棕子比赛,四、五、六年级代表队完成粽子的个数比为4∶5∶6,已知四年级代表队包了60个棕子,三个代表队一共包了多少个棕子?
28.端午节是中国四大传统节日之一,端午文化在世界上影响广泛,吃粽子是端午节的一项重要习俗。下面图表是某超市端午节当天所销售粽子的一些信息,请根据图表中信息解答下面的问题。
单价/元 数量/个 总价/元
A品牌 400
B品牌 600
C品牌 2.5
合计 4900
(1)B品牌粽子数量占粽子总数的( )%。
(2)请计算C品牌粽子的总个数和总价,并填入表中。
(3)已知A品牌粽子单价是B品牌粽子单价的,那么A、B品牌的粽子单价各多少元?(列方程解答)
参考答案:
1.D
【分析】两种相关联的量,若它们的比值一定,两种量成正比例关系;若它们的乘积一定,两种量成反比例关系。
【详解】A.m和n的比值一定,m和n成正比例关系。
B.根据=m,得=2,比值一定,m和n成正比例关系。
C.根据=,得=,比值一定,m和n成正比例关系。
D.根据=8,得mn=,乘积一定,m和n成反比例关系。
故答案为:D
【点睛】辨识两种量成正比例还是成反比例,就看两种量的比值一定还是乘积一定。
2.A
【分析】本题可以用抽屉原理的最不利原则;故意在3个墙面上涂上甲、乙、丙3种颜色,没有重复,但第4面墙只能选甲、乙、丙中的一种,至少有两面的颜色是一致的;所以得出颜料的种数是3种。
【详解】4-1=3(种)
故答案为:A
【点睛】此题属于抽屉原理的习题,做题时应确定哪个是抽屉,哪个相当于物体个数,然后可利用抽屉原理的最不利原则进行分析即可。
3.C
【分析】根据题意,把上衣原价看作单位“1”,则涨降价后的价格=原价×(1+),求出涨价后的价格后,把这个价格看作单位“1”,现在的价格=涨价后的价格×(1-),求出即可。
【详解】96×(1+)
=96×
=24×5
=120(元)
120×(1-)
=120×
=90(元)
故答案为:C
【点睛】此题答题的关键是分清前后两个单位“1”的区别,再由此列出数量关系解答。
4.D
【分析】首先要求出堆成的正方体的棱长是多少厘米,也就是要求出20、15、6的最小公倍数,这个数就是堆成的正方体的棱长;再分别用棱长除以原来的长、宽、高,求出长要堆几块,宽要堆几块,高要堆几块,最后用这三个块数相乘就得到需要的总块数。
【详解】20、15和6的最小公倍数是60
60÷20=3(块)
60÷15=4(块)
60÷6=10(块)
3×4×10=120(块)
故答案为:D
【点睛】此题主要考查正方体的特征,以及最小公倍数的应用。
5.B
【分析】足球与篮球的数量比是7∶2,则篮球占总数的,则可以据此算出篮球的个数。
又买进一些足球后,足球占总数的80%,则篮球占总数的1-80%=20%,用篮球的数量可以算出足球和篮球的总数。
【详解】36×=8(个)
8÷(1-80%)
=8÷20%
=40(个)
故答案为:A
【点睛】解答此题的关键是找到不变的量,即前后没有变化的是篮球的个数。再根据篮球所占总数的百分比可以求出答案。
6. 2 3 5.028
【分析】根据1时=60分,1吨=1000千克,进行换算即可。
【详解】0.05×60=3(分),2.05时=2时3分;28÷1000=0.028(吨),5吨28千克=5.028吨
【点睛】单位大变小乘进率,单位小变大除以进率。
7. 75
【分析】求比100米少25%的数是多少,用100-100×25%即可解答;求比8千克多千克是多少,用加法解答即可。
【详解】100-100×25%
=100-25
=75(米)
8+=(千克)
【点睛】本题考查求比一个数少百分之几的数是多少,明确单位“1”是解题的关键。
8. 8 5
【分析】根据比例的基本性质可知,两内项之积等于两外项之积,可得5x=8y,把5和x看作比例的两个外项,把8和y看作比例的两个内项,即可写出比例式。
【详解】根据分析得,如果,5x=8y,
可写成比例式:x∶y=8∶5。
【点睛】此题的解题关键是灵活运用比例的基本性质求解。
9.500
【分析】将原价看作单位“1”,打七五折销售,现价是原价的75%,比原来便宜了1-75%,原价×便宜的对应百分率=便宜的钱数,据此分析。
【详解】2000×(1-75%)
=2000×0.25
=500(元)
【点睛】关键是理解折扣的意义,几折就是百分之几十。
10.414
【分析】由题意可知,根据圆的周长公式:C=πd,据此可求出底面圆的直径,这根丝带的长度=8条直径的长度+8条高的长度+接头处的长度,据此解答即可。
【详解】94.2÷3.14=30(cm)
30×8+8×18+30
=240+144+30
=384+30
=414(cm)
【点睛】本题考查圆的周长,明确彩带都是由哪几部分构成的是解题的关键。
11. 18 216
【分析】根据长方形的周长=(长+宽)×2,可得长+宽=60÷2=30(cm),已知长和宽的比是3∶2,长可看作3份,宽看作2份,长和宽共占(3+2)份,可求出长占长和宽总长的,利用求一个数的几分之几是多少的计算方法,用30×求出长方形的长,继而求出长方形的宽,再利用长方形的面积公式,代入数据即可得解。
【详解】60÷2=30(cm)
30×=30×=18(cm)
30-18=12(cm)
18×12=216(cm2)
【点睛】此题主要考查按比例分配的应用题的解答方法,利用长方形的周长和面积公式,解决实际的问题。
12. 2400 2412
【分析】药粉和水的比是1∶200,即水的质量是药粉的200倍,所以用药粉乘200求出需要加的水,再用水加药粉就等于药水。
【详解】12×200=2400(千克)
2400+12=2412(千克)
【点睛】本题考查了比的问题,关键是根据比的意义先求出水的质量。
13. 8 24
【分析】根据正方体的体积公式:V=a3,求出水的体积,然后根据圆柱的体积公式:V=Sh,据此可求出圆柱形容器的高;再根据圆锥的体积公式:V=Sh,据此求出圆锥形容器的高。
【详解】4×4×4÷8
=16×4÷8
=64÷8
=8(dm)
4×4×4×3÷8
=64×3÷8
=192÷8
=24(dm)
【点睛】本题考查圆柱和圆锥的体积,熟记公式是解题的关键。
14.√
【分析】要比较这几个城市的气温高低,就要比较这几个城市气温的数值的大小。在数轴上,从左到右的顺序,就是数从小到大的顺序。这几个数值在数轴上从左到右依次是:﹣20、﹣6、15,据此解答。
【详解】因为﹣20<﹣6<15,即在数轴上,﹣20位于最左边,因为越往左,数越小,所以乙市的气温最低。原题说法正确。
故答案为:√
【点睛】本题主要考查正、负数的大小比较,要求学生熟练掌握。
15.√
【分析】根据实际距离=图上距离÷比例尺,再结合已知比例尺:1∶30000,求出当图上长度为1厘米的实际长度,然后跟题中结果对比即可。
【详解】1÷=30000(厘米)
30000厘米=300米
所以图上1厘米表示实际300米;
故答案为:√
【点睛】本题主要考查比例尺的意义,熟练掌握比例尺的意义并灵活运用。
16.√
【分析】假设原来圆柱的底面周长为6.28,高为8,则变化后圆柱的底面周长为(6.28×2),高为(8×),根据圆的周长公式:C=2πr,圆柱的体积公式:V=πr2h,据此求出圆柱变化前后的体积,再进行对比即可。
【详解】假设原来圆柱的底面周长为6.28,高为8
6.28÷3.14÷2
=2÷2
=1
3.14×12×8
=3.14×1×8
=3.14×8
=25.12
变化后圆柱的底面周长为:6.28×2=12.56
高为8×=2
12.56÷3.14÷2
=4÷2
=2
3.14×22×2
=3.14×4×2
=12.56×2
=25.12
则圆柱的底面周长扩大到原来的2倍,高缩小到原来的,体积不变。说法正确。
故答案为:√
【点睛】本题考查圆柱的体积,熟记公式是解题的关键。
17.×
【分析】设长方形的长和宽分别是a和b,那么原来的面积为ab,现在的面积为(1+20%)a×(1-20%)b,即0.96ab,进行比较即可解答。
【详解】设长方形的长为a,宽为b。
原来面积:
a×b=ab
现在面积:
(1+20%)a×(1-20%)b
=1.2a×0.8b
=0.96ab
ab>0.96ab
故答案为:×
【点睛】解答本题的关键是求出长方形变化前后的面积,进而进行判断。
18.×
【分析】平均数×个数=总数,总数÷总份数=一份数,一份数×最小数对应份数=最小的数,据此分析。
【详解】35×3÷(4+7+10)×4
=105÷21×4
=20
最小的数是20。
故答案为:×
【点睛】关键是理解平均数和比的意义。
19.1.25;;2;0;
;;0.72;
【详解】略
20.12;16
1;3.15
【分析】根据乘法分配律将原式转化成(54+41+1)×进行简算;
根据乘法分配律将原式转化成×(101-1)进行简算;
先算小括号里的加法,再算小括号外中括号里的减法,最后算中括号外的除法;
先算3.75×10%结果为0.375,将其转化成分数为,根据减法的性质,将原式转化成4.15-(+),先算小括号里的加法,再算小括号外的减法即可。
【详解】
=×54+×41+×1
=(54+41+1)×
=96×
=12
=×101-×1
=×(101-1)
=×100
=16
=[2-(+)]÷
=[2-]÷
=÷
=×
=1
=4.15--
=4.15-(+)
=4.15-1
=3.15
21.(1);(2)x=9.6;(3)
【分析】
(1)根据比例的基本性质,把式子转化为,再化简方程,最后根据等式的性质,方程两边同时除以即可;
(2)根据比例的基本性质,把式子转化为5x=4×12,再化简方程,最后根据等式的性质,方程两边同时除以5即可;
(3)先化简比例,根据比例的基本性质,把式子转化为,再化简方程,最后根据等式的性质,方程两边同时除以即可。
【详解】
(1)
解:
(2)
解:5x=4×12
5x=48
5x÷5=48÷5
x=9.6
(3)
解:
22.175.84dm3
【分析】根据圆锥的体积公式,用底面直径为8dm,高为12dm的圆锥的体积减去底面直径为4dm,高为6dm的圆锥的体积,根据圆锥的体积公式:V=πr2h,把数据代入公式解答。
【详解】×3.14×(8÷2)2×12-×3.14×(4÷2)2×6
=×3.14×16×12-×3.14×4×6
=200.96-25.12
=175.84(dm3)
23.100人;80人
【分析】将四年级人数看作单位“1”,六年级人数是四年级的(1+25%),六年级人数÷对应百分率=四年级人数;将四年级人数看作单位“1”,五年级人数是四年级的(1-20%),四年级人数×五年级对应百分率=五年级人数。
【详解】
(人)
(人)
答:四年级学生有100人,五年级学生有80人。
24.优惠卡购买;理由见详解
【分析】分别计算出按优惠卡购买需要支付的总价和按原价购买需要支付的总价,选择总价最少的方式购买花费最少。
原价购买:根据总价=单价×数量,代入相应数值计算;
优惠卡购买:打八折,即现价是原价的80%,先计算出以单价48元购买20本电脑书的总价钱,再用总价钱乘80%,所得结果再加上购买优惠卡40元,即为按优惠卡购买需付的钱数。
【详解】原价购买:48×20=960(元)
优惠卡购买:48×20×80%+40
=960×0.8+40
=768+40
=808(元)
因为808<960,所以按优惠卡购买需要支付的费用最少,因此选择按优惠卡购买。
25.62.8平方米
【分析】滚筒滚动一周的面积就是这个圆柱形的侧面积,利用圆柱的侧面积=圆柱的底面周长×宽=,即可求得一周压过的路面面积,每分钟转10周,即乘10即可。
【详解】
(平方米)
6.28×10=62.8(平方米)
答:滚筒一分压过的路面是62.8平方米。
【点睛】
26.174千米
【分析】本题根据实际距离=图上距离÷比例尺,代入数据计算即可,注意单位换算。
【详解】(厘米)
17400000厘米=174千米
答:京张高铁实际全线长174千米。
27.225个
【分析】由已知可得,四年级代表队完成粽子的份数为4,个数为60,可算出每份的个数为:60÷4=15(个),再算出三个年级代表队完成粽子的总份数为4+5+6=15,再用每份的个数乘总份数,即15×15=225(个),据此解答。
【详解】60÷4×(4+5+6)
=15×15
=225(个)
答:三个代表队一共包了225个棕子。
28.(1)30%
(2)1000个;2500元;见详解
(3)1.5元;3元
【分析】(1)把三个品牌的总数看作单位“1”,用单位“1”减去C品牌和A品牌所占总数的百分率,即可求出B品牌的百分率;
(2)已知A品牌的粽子销售400个,A品牌的粽子占总数的20%,已知一个数的百分比是多少求这个数,用除法计算,即用400除以20%,先算出三种品牌粽子的总数,再减去A品牌和B品牌粽子销售量的和,即可求出C品牌粽子销售量并填表,再根据总价=单价×数量,求出总价即可并填表即可。
(3)A品牌粽子单价是B品牌粽子单价的,设B品牌粽子单价为x,则A品牌粽子单价是x,再根A品牌粽子总价+B品牌粽子总价=三种品牌粽子的总价减去C品牌粽子总价;据此列方程解答即可。
【详解】(1)1-50%-20%
=50%-20%
=30%
即B品牌粽子数量占粽子总数的30%。
(2)400÷20%=2000(个)
2000-(600+400)
=2000-1000
=1000(个)
1000×2.5=2500(元)
答:C品牌粽子的总个数是1000个,总价是2500元;
填表如下:
单价/元 数量/个 总价/元
A品牌 400
B品牌 600
C品牌 2.5 1000 2500
合计 4900
(3)解:设B品牌粽子单价为x,则A品牌粽子单价是x;
600x+400×x=4900-2500
600x+200x=2400
800x=2400
800x÷800=2400÷800
x=3(元)
3×=1.5(元)
答:A品牌的粽子单价1.5元;B品牌的粽子单价3元。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
