小升初分班考精选题检测卷(试题)2023-2024学年数学六年级下册青岛版(含答案)
文档属性
| 名称 | 小升初分班考精选题检测卷(试题)2023-2024学年数学六年级下册青岛版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 929.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-29 08:55:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考精选题检测卷(试题)2023-2024学年数学六年级下册青岛版
一、选择题
1.下面各数中的“6”,表示6个十分之一的是( )。
A.1.60 B.1.06 C.1.006 D.60.1
2.在计算14×12时,小红是这样想的:14×10=140,14×2=28,140+28=168。下面能表示她思考过程的图是( )。
A. B.
C. D.
3.学校买来8个足球,每个a元,又买来b个篮球,每个56元,学校买足球和篮球一共花( )元。
A.8×(a+b) B.56×(a+b) C.8a+56b D.8+a+56+b
4.如图,水平放置的甲、乙两个盘子分别由若干个相同的黑色和白色等边三角形区域组成。随意向甲、乙两个盘子各抛一个小球,小球停在甲中黑色三角形区域的可能性记为a,停在乙中黑色三角形区域的可能性记为b,则( )。
甲 乙
A.a>b B.a<b C.a=b D.无法确定
5.下图以雷达站为观测点,鱼雷艇在( )方向。
A.北偏东30° B.北偏西30° C.东偏北60° D.东偏北30°
6.一件毛衣先提价10%,再降价10%,现价与原价相比,( )。
A.不变 B.降低了 C.提高了 D.要看实际价格
7.设计人员把一个长5mm的零件画在图纸上长为25cm,这幅图纸的比例尺是( )。
A.1∶5 B.5∶1 C.50∶1 D.1∶50
8.如图中,瓶底的面积与杯口面积相等,将瓶中的液体倒入杯子中,能倒满( )杯。
A.2 B.3 C.6 D.8
二、填空题
9.袁隆平爷爷被誉为中国“杂交水稻之父”,在国际社会,杂交水稻被誉为“中国第五大发明”。上世纪70年代,中国杂交水稻产量就已高出常规水稻20%左右。每年增产的粮食能多养活70000000人。为80多个发展中国家培训了14000多名杂交水稻技术人才。如今全球40多个国家,800万公顷的大面积种植,足以说明问题。“万家粮食中国粮”,袁隆平的实践表明∶中国人不仅能将饭碗牢牢端在自己手里,还能帮助世界人民解决吃饭问题。
若用x表示常规水稻产量,那么中国杂交水稻产量为( )。
70000000=( )万 800万公顷=( )平方千米
10.一个四位数120同时能被2、3、5整除,则中可以填写( )。
11.的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是最小的质数。
12.根据8x=3y组成一个比例x∶y=( )∶( )
13.“六一”儿童节那天,幼儿园买来了许多的苹果、桃子、桔子和香蕉,每个小朋友可以任意选择一种水果,那么至少要有( )个小朋友才能保证有两人选的水果是相同的。
14.在一个正方形内画一个最大的圆,这个圆的周长为25.12厘米,这个正方形面积是( )平方厘米。
15.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米,一位同学去洗手,走时忘记关水龙头,5分钟后另一位同学发现并关掉了水龙头,共浪费了( )升水。
16.一个圆锥的底面直径和高都是4分米,如果沿着底面直径切成两半,表面积增加( )平方分米。
三、判断题
17.用3厘米、6厘米、3厘米的三根小棒可以围成一个等腰三角形。( )
18.加工一批零件,经检验有100个合格,不合格的有25个,这个零件的合格率是75%。( )
19.一个比例里,两个外项的积是1,则两个内项互为倒数。( )
20.所有的负数都比0小。( )
21.正方体的棱长扩大2倍,体积就扩大6倍。( )
四、计算题
22.直接写得数。
713+159= 605-378= 5.06×4= 32.8÷10=
0.68-0.32= 8×12.5%=
23.计算下面各题,怎样简便就怎样算。
276+476-276+52 44×80%×2.5×12.5
24.解方程。
(1) (2)∶x (3)0.2x+5%x=18
25.计算下面图形阴影部分的周长和面积。
五、解答题
26.张村有一块试验田种水稻,今年换种新品种后,产量是2600千克,今年产量比去年增产三成,去年的产量是多少千克?
27.甲乙两车分别从、两地同时相向而行,甲每小时行80千米,乙每小时行全程的,当乙行到全程的时,甲车再行全程的,可到达地。求、两地相距多少千米?
28.一个底面直径是10厘米、高是12厘米的圆柱形玻璃容器里装有一些水,水中浸没着一个底面直径是6厘米,高10厘米的圆锥形铁块,如果把铁块从水中取出,那么容器中水面高度将下降多少厘米?
29.港珠澳大桥是世界上最长的跨海大桥。主体工程连接桥梁和海底隧道的东、西人工岛。岛体结构采用深插式大直径钢圆筒和抛石斜坡堤组合结构。东人工岛使用钢圆筒59个,西人工岛使用钢圆筒61个。每个钢圆筒平均长度是55米。两个人工岛使用钢圆筒的总长度是多少米?
30.某物流公司将120吨货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载重量与所需车辆的数量如下表。
载重量/吨 2.5 3 5 10
数量/辆 48 40 _____ _____
(1)将上表填写完整。
(2)车辆的载重量和所需车辆的数量成什么比例关系?为什么?
(3)如果用载重量为6吨的卡车来运,一共需要多少辆?
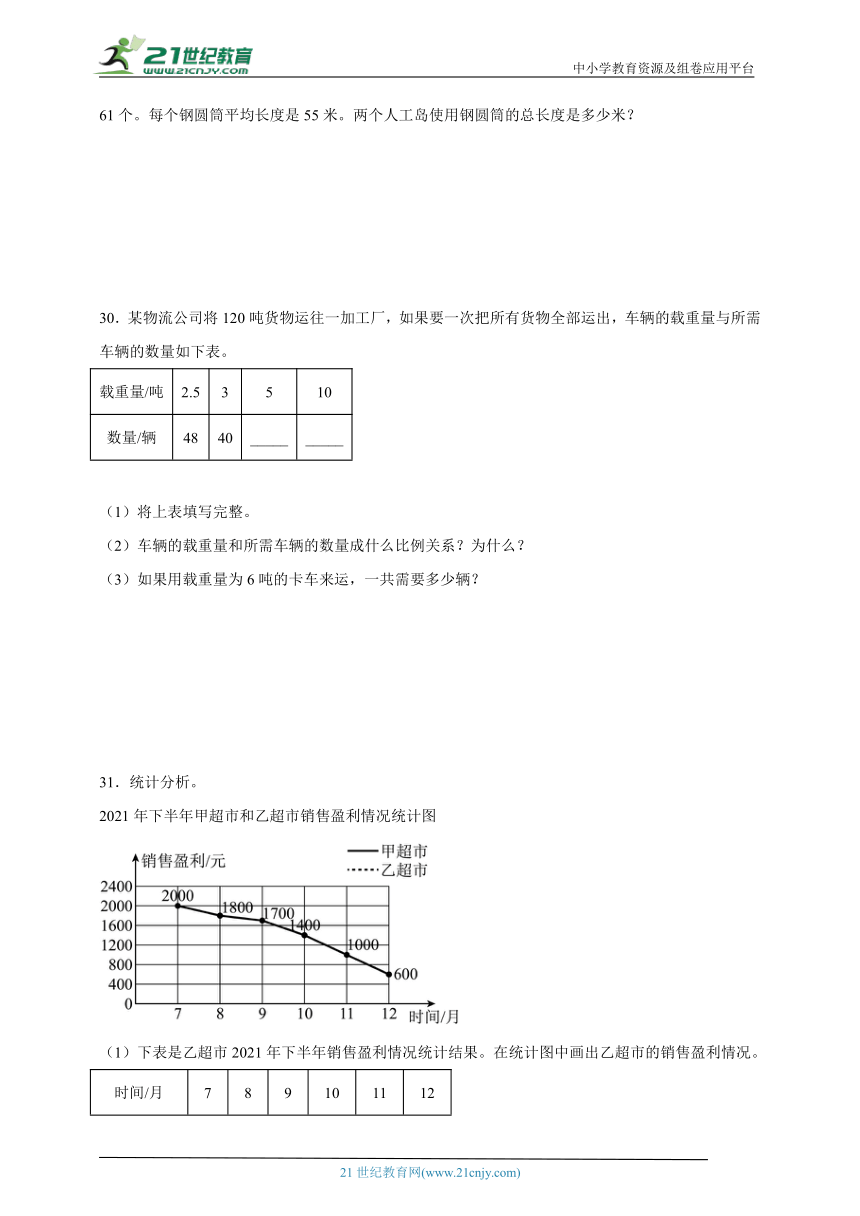
31.统计分析。
2021年下半年甲超市和乙超市销售盈利情况统计图
(1)下表是乙超市2021年下半年销售盈利情况统计结果。在统计图中画出乙超市的销售盈利情况。
时间/月 7 8 9 10 11 12
销售盈利/元 200 400 800 1200 1800 2000
(2)从上图中可以看出,2021年下半年甲超市的销售盈利情况呈( )趋势。乙超市的销售盈利情况呈( )趋势。(填“上升”或“下降”)
(3)9月份甲超市的销售盈利额度比乙超市多( )%。
参考答案:
1.A
【分析】根据数的组成,每一个数位上数字是几就表示有几个这样的计数单位,据此逐项分析即可。
【详解】A.1.60中的“6”在十分位上,表示6个十分之一;
B.1.06中的“6”在百分位上,表示6个百分之一;
C.1.006中的“6”在千分位上,表示6个千分之一;
D.60.1中的“6”在十位上,表示6个十。
故答案为:A
【点睛】解答本题的关键是掌握各个数位的计数单位。
2.B
【分析】小红计算14×12时,将12拆成10和2,分别将这两个数与14相乘,再将乘积加起来。
【详解】能表示她思考过程的图是。
故答案为:B。
【点睛】计算两位数乘两位数数,可以将其中一个两位数拆成整十数和一位数,分别求出这两个数与另一个两位数相乘,再将乘积加起来即可。
3.C
【分析】根据“总价=单价×数量”表示出购买8个足球和b个篮球各需要多少元,最后相加求和,据此解答。
【详解】购买8个足球的钱数:8a(元)
购买b个篮球的钱数:56b(元)
学校买足球和篮球的总钱数:(8a+56b)元
故答案为:C
【点睛】掌握单价、数量、总价之间的关系是解答题目的关键。
4.C
【分析】可能性的数值表示:通常概率用英文字母P来表示,记作:P(事件)。可能性的计算步骤:列出所有可能发生的结果,并判定每个结果发生的可能性都相等;再确定所有可能发生的结果个数n和其中出现所求事件的结果个数m;最后计算所求事件发生的可能性(概率),公式为:
分别算出甲、乙两个盘子小球停在黑色区域的可能性,分析可知黑色区域的可能性就是黑色占整个盘子的几分之几,再比较大小即可。
【详解】甲:将盘子平均分成6份,黑色区域是2份,则a=;
乙:将盘子平均分成9份,黑色区域是3份,则b=;
a=b
故答案为:C
5.D
【分析】确定观测点,判断被观测点区域,然后结合数据写出位置。
【详解】雷达站为观测点,是从雷达站观看鱼雷艇,根据上北下南,左西右东,鱼雷艇在东北区域,根据图形数据30°,鱼雷艇在雷达站东偏北30°方向或北偏东60°的方向。
故答案为:D
【点睛】此题考查用方位角表示位置,关键判断观测点与偏向角度数。
6.B
【分析】把这件毛衣的原价看作单位“1”,现价占原价的(1+10%)×(1-10%),假设出原价并求出这件毛衣的现价,最后比较大小,据此解答。
【详解】假设这件毛衣的原价为1。
1×(1+10%)×(1-10%)
=1.1×0.9
=0.99
因为0.99<1,所以现价比原价低。
故答案为:B
【点睛】第一个10%的单位“1”是商品的原价,第二个10%的单位“1”是商品提价10%后的价格,注意二者的区别。
7.C
【分析】根据图上距离∶实际距离=比例尺,据此解答即可。
【详解】5mm=0.5cm
25∶0.5=(25×4)∶(0.5×4)
=100∶2
=(100÷2)∶(2÷2)
=50∶1
故答案为:C
【点睛】本题考查比例尺,明确图上距离∶实际距离=比例尺是解题的关键。
8.C
【分析】等底等高的圆锥的体积是圆柱的,那么瓶中一半液体倒入杯中能倒满3杯,瓶中液体全倒入杯中,可以倒6杯。
【详解】由分析知:
令圆柱的高为2,则圆锥的高为1,瓶子底面和杯口面积相等等于S
则圆柱体积为:2S
圆锥的体积为:1×S
2S6(杯)
所以能倒满6杯。
故选:C
【点睛】此题考查了圆柱和圆锥的体积公式的灵活应用。
9. 120%x 7000 8万
【分析】将常规水稻产量看作单位“1”,从中国杂交水稻产量高出常规水稻20%左右,可以得出中国杂交水稻产量是常规水稻的(1+20%),求一个数的百分之几是多少,用乘法计算;70000000的计数单位是1,换算为“万”做单位,小数点移动4位即可求出答案;由1平方千米=100公顷,低级单位转变高级单位除以进率可以求出答案。
【详解】(1)x×(1+20%)
=x×120%
=120%x或1.2x
(2)70000000÷10000=7000,70000000=7000(万)
(3)800÷100=8,800万公顷=8万平方千米。
【点睛】此题考查求一个数多百分之几是多少与字母代表数的运用以及单位进率换算。
10.0、3、6、9
【分析】
2的倍数的数的特征是:个位上是0、2、4、6、8的数;3的倍数的数的特征是:各位上的数字之和是3的倍数,这个数就是3的倍数;5的倍数的数的特征是:个位上是0或5的数都是5的倍数;120个位上是0,所以已经满足同时能被2、5整除,所以只需要满足这个数是能被3整除即可;由此解答。
【详解】
120个位上的数是0,能同时被2、5整除;
1+2+0+0=3
1+2+3+0=6
1+2+6+0=9
1+2+9+0=12
填入0、3、6、9时,12能被3整除。
所以里填0、3、6、9,能同时被2、3、5整除。
【点睛】此题主要考查2、3、5的倍数的特征。
11. 8 2
【分析】将单位“1”平均分成若干份,表示其中这样一份的数为分数单位。
据此可知,的分数单位是,它含有8个这样的分数单位;
最小的质数是2,2-=。
所以再添上2个这样的分数单位就是最小的质数。
【详解】根据分数单位的意义可知,的分数单位是,它含有8个这样的分数单位;
最小的质数是2,2-=,所以再添上2个这样的分数单位就是最小的质数。
【点睛】求一个带分数含有多少个分数单位时,要先将这个带分数化为假分数。
12. 3 8
【分析】从x∶y=( )∶( )中可知:x是外项,y是内项;利用比例的基本性质:两外项的积等于两内项的积,则8是外项,3是内项;据此填空。
【详解】根据分析可知:
根据8x=3y组成一个比例x∶y=3∶8。
13.5
【分析】有4种水果,每个小朋友任意选择一种有4种选择方法,最差情况是4个小朋友选择的水果都不相同,此时只要再有一个小朋友任意选择一种水果,就能保证有两人选的水果是一样的,据此解答。
【详解】4+1=5(个)
所以,至少要有5个小朋友才能保证有两人选的水果是相同的。
【点睛】掌握抽屉原理的解题方法是解答题目的关键。
14.64
【分析】由圆的周长公式C=πd,得d=C÷2,由此求出圆的直径,而此圆是一个正方形内所画的一个最大的圆,所以圆的直径就是正方形的边长,再根据正方形的面积公式S=a×a,列式求出这个正方形的面积。
【详解】正方形的边长:25.12÷3.14=8(厘米)
正方形的面积:8×8=64(平方厘米)
【点睛】解答本题的关键是知道在一个正方形内所画最大圆的直径是正方形的边长,再灵活利用圆的周长公式与正方形的面积公式解决问题。
15.7.536
【分析】先求出5分钟从水管流出的水的长度,再利用圆柱的体积=底面积×高,即可求出浪费的水的体积。
【详解】5分钟=300秒
2厘米=0.2分米
8厘米=0.8分米
3.14×(0.2÷2)2×(0.8×300)
=3.14×2.4
=7.536(立方分米)
=7.536升
共浪费7.536升。
【点睛】本题重点考查学生对实际生活中数学问题转化为数学公式的能力,强化圆柱体积公式的实际应用。
16.16
【分析】根据题意表面积增加的部分为底是4分米,高也是4分米的两个三角形的面积,据此解答。
【详解】4×4÷2×2=16(平方分米),表面积增加16平方分米。
故答案为:16。
【点睛】解答此题的关键是明确圆锥沿底面直径切成两半,增加的是两个完全一样的三角形,并且三角形的底是圆锥的直径,高是圆锥的高。
17.×
【分析】根据三角形的三边关系:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【详解】因为3+3=6,所以不能围成三角形;原题说法错误。
故答案为:×
【点睛】此题关键是根据三角形的三边关系进行分析、解答。
18.×
【分析】先理解合格率,合格率是指合格的零件个数占零件总个数的百分之几,计算方法为:合格零件数÷零件总个数×100%=合格率,由此代入数据列式解答。
【详解】100÷(100+25)×100%
=100÷125×100%
=80%
故原题干说法错误。
【点睛】此题属于典型的百分率问题,都是用一部分数量(或全部数量)除以全部数量乘百分之百,计算时一定要找准对应量。
19.√
【分析】根据比例的基本性质:两外项之积等于两内项之积,可以知道两个内项的积也是1,再根据倒数的定义:乘积是1的两个数互为倒数进行判断。
【详解】两个外项的积是1,那么两个内项的积也是1,乘积为1的两个数互为倒数,所以两个内项互为倒数,原题说法正确。
故答案为:√
【点睛】熟练掌握比例的基本性质和倒数的意义是解答本题的关键。
20.√
【分析】根据负数的认识,比0小的数叫负数,进行分析。
【详解】所有的负数都比0小,说法正确。
故答案为:√
【点睛】0是正数和负数的分界点,0不是正数也不是负数。
21.×
【分析】设原来的棱长是1,棱长扩大2倍后是2,分别计算体积,然后确定体积扩大的倍数,再进行判断。
【详解】设原来的棱长是1,棱长扩大2倍后是2;
对比发现,体积扩大8倍,故题干阐述错误
故答案为:×。
【点睛】正方体的棱长扩大2倍,棱长和扩大2倍,表面积扩大4倍,体积扩大8倍。
22.872;227;20.24;3.28;
;0.36;1;
【详解】略
23.528;1100;
【分析】(1)按照加法交换律和结合律计算;
(2)按乘法交换律和结合律计算;
(3)先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的乘法。
【详解】(1)276+476-276+52
=(276-276)+(476+52)
=0+528
=528
(2)44×80%×2.5×12.5
=(44×2.5)×(80%×12.5)
=(11×4×2.5)×10
=110×10
=1100
(3)×[(-)÷]
=×[(÷]
=×
=
24.(1)y=1.65;(2)x=;(3)x=72
【分析】(1)根据比例的基本性质,把比例化为方程,两边再同时除以3;
(2)根据比例的基本性质,把比例化为方程,两边再同时乘;
(3)先把方程左边化简为0.25x,两边再同时乘4。
【详解】(1)
解:3y=1.1×4.5
3y÷3=1.1×4.5÷3
y=1.65
(2)∶x
解:x=
x=
x=
(3)0.2x+5%x=18
解:0.25x=18
4×0.25x=18×4
x=72
25.周长48.56dm,面积78.88dm2
【分析】观察图形可得:阴影部分的周长=直径是8dm的圆的周长+10dm的边长×2+16dm的边长,然后再根据圆的周长公式C=πd进行解答;
阴影部分的面积=上底为10dm、下底为16dm、高为8dm的梯形的面积-直径是8dm的半圆的面积,然后再根据梯形的面积公式S=(a+b)h÷2,圆的面积公式S=πr2进行解答。
【详解】×3.14×8+10×2+16
=12.56+36
=48.56(dm)
(10+16)×8÷2-3.14×(8÷2)2÷2
=104-25.12
=78.88(dm2)
26.2000千克
【分析】根据条件“ 今年换种新品种后,产量是2600千克,今年产量比去年增产三成 ”可知,去年的产量×(1+30%)=今年的产量,已知今年的产量,要求去年的产量,用除法计算,据此列式解答。
【详解】三成=30%;
2600÷(1+30%)
=2600÷1.3
=2000(千克)
答:去年的产量是2000千克。
【点睛】此题主要考查了成数的应用,明确去年产量和今年产量的关系是解答本题的关键。
27.600千米
【分析】根据题意,把两地之间的路程看作单位“1”,已知甲每小时行80千米,乙每小时行全程的,当乙行到全程的时,甲车再行全程的,也就是乙行到全程的时,甲行了全程的;根据在相同时间内,所行路程的比等于速度的比,由此求出甲乙速度的比是:(1-)∶=4∶3,已知甲每小时行80千米,这样就可以求出乙的速度,根据已知一个数的百分之几是多少,求这个数,用除法解答即可。
【详解】甲乙速度比是:(1-)∶=4∶3
所以乙车每小时的速度是:
(千米)
两地相距:
(千米)
答:、两地相距600千米。
【点睛】解答此题关键是把两地之间的路程看作单位“1”,求出甲乙速度的比,由甲每小时行80千米,就可以求出乙的速度,由此解决问题。
28.1.2厘米
【分析】根据题意可知,把圆锥形铁块从圆柱形玻璃容器中取出后,水面下降的高等于圆锥的体积除以圆柱的底面积。根据圆锥的体积公式:,圆的面积公式:,代入数据进行解答即可。
【详解】×3.14×(6÷2)2×10÷[3.14×(10÷2)2]
=×3.14×9×10÷[3.14×25]
=×28.26×10÷78.5
=9.42×10÷78.5
=94.2÷78.5
=1.2(厘米)
答:容器中水面高度将下降1.2厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,圆的面积公式及应用,关键是熟记公式。
29.6600米
【分析】要求两个人工岛使用钢圆筒的总长度是多少米,先分别计算出两个人工岛使用的钢圆筒的长度,再相加即可。
【详解】59×55=3245(米)
61×55=3355(米)
3245+3355=6600(米)
答:两个人工岛使用钢圆筒的总长度是6600米。
【点睛】本题考查乘法在实际中的应用,弄清题目中的数量关系是关键。
30.(1)24;12
(2)反比例;见详解
(3)20辆
【分析】(1)已知货物总吨数是120吨,根据所需的车辆数量=货物的总吨数÷车辆的载重量,即可求出统计表中载重量是5吨、10吨时所需的车辆数量,进而把表格填完整。
(2)判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
(3)用货物的总吨数除以车辆的载重量,即可求出所需车辆的数量。
【详解】(1)120÷5=24(辆)
120÷10=12(辆)
如下表:
载重量/吨 2.5 3 5 10
数量/辆 48 40 24 12
(2)2.5×48=3×40=5×24=10×12=120(一定)
乘积一定,车辆的载重量与所需车辆的数量成反比例关系。
(3)120÷6=20(辆)
答:一共需要20辆。
【点睛】本题考查正、反比例的意义及辨识方法,同时能运用统计表中提供的信息解决问题。
31.(1)见详解
(2)下降;上升
(3)112.5%
【分析】(1)观察折线统计图,横轴代表时间,纵轴代表销售盈利,然后根据统计表在统计图中标出相应的点,然后顺次连接即可;
(2)根据折线统计图中两条线的变化趋势填空即可;
(3)先求出9月份甲超市的销售盈利额度比乙超市多多少,再除以乙超市9月份销售盈利额度即可。
【详解】(1)如图所示:
(2)2021年下半年甲超市的销售盈利情况呈下降趋势。乙超市的销售盈利情况呈上升趋势。
(3)(1700-800)÷800
=900÷800
=112.5%
9月份甲超市的销售盈利额度比乙超市多112.5%。
【点睛】本题考查求一个数比另一个数多百分之几,明确单位“1”是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考精选题检测卷(试题)2023-2024学年数学六年级下册青岛版
一、选择题
1.下面各数中的“6”,表示6个十分之一的是( )。
A.1.60 B.1.06 C.1.006 D.60.1
2.在计算14×12时,小红是这样想的:14×10=140,14×2=28,140+28=168。下面能表示她思考过程的图是( )。
A. B.
C. D.
3.学校买来8个足球,每个a元,又买来b个篮球,每个56元,学校买足球和篮球一共花( )元。
A.8×(a+b) B.56×(a+b) C.8a+56b D.8+a+56+b
4.如图,水平放置的甲、乙两个盘子分别由若干个相同的黑色和白色等边三角形区域组成。随意向甲、乙两个盘子各抛一个小球,小球停在甲中黑色三角形区域的可能性记为a,停在乙中黑色三角形区域的可能性记为b,则( )。
甲 乙
A.a>b B.a<b C.a=b D.无法确定
5.下图以雷达站为观测点,鱼雷艇在( )方向。
A.北偏东30° B.北偏西30° C.东偏北60° D.东偏北30°
6.一件毛衣先提价10%,再降价10%,现价与原价相比,( )。
A.不变 B.降低了 C.提高了 D.要看实际价格
7.设计人员把一个长5mm的零件画在图纸上长为25cm,这幅图纸的比例尺是( )。
A.1∶5 B.5∶1 C.50∶1 D.1∶50
8.如图中,瓶底的面积与杯口面积相等,将瓶中的液体倒入杯子中,能倒满( )杯。
A.2 B.3 C.6 D.8
二、填空题
9.袁隆平爷爷被誉为中国“杂交水稻之父”,在国际社会,杂交水稻被誉为“中国第五大发明”。上世纪70年代,中国杂交水稻产量就已高出常规水稻20%左右。每年增产的粮食能多养活70000000人。为80多个发展中国家培训了14000多名杂交水稻技术人才。如今全球40多个国家,800万公顷的大面积种植,足以说明问题。“万家粮食中国粮”,袁隆平的实践表明∶中国人不仅能将饭碗牢牢端在自己手里,还能帮助世界人民解决吃饭问题。
若用x表示常规水稻产量,那么中国杂交水稻产量为( )。
70000000=( )万 800万公顷=( )平方千米
10.一个四位数120同时能被2、3、5整除,则中可以填写( )。
11.的分数单位是( ),它有( )个这样的分数单位,再添上( )个这样的分数单位就是最小的质数。
12.根据8x=3y组成一个比例x∶y=( )∶( )
13.“六一”儿童节那天,幼儿园买来了许多的苹果、桃子、桔子和香蕉,每个小朋友可以任意选择一种水果,那么至少要有( )个小朋友才能保证有两人选的水果是相同的。
14.在一个正方形内画一个最大的圆,这个圆的周长为25.12厘米,这个正方形面积是( )平方厘米。
15.自来水管的内直径是2厘米,水管内水的流速是每秒8厘米,一位同学去洗手,走时忘记关水龙头,5分钟后另一位同学发现并关掉了水龙头,共浪费了( )升水。
16.一个圆锥的底面直径和高都是4分米,如果沿着底面直径切成两半,表面积增加( )平方分米。
三、判断题
17.用3厘米、6厘米、3厘米的三根小棒可以围成一个等腰三角形。( )
18.加工一批零件,经检验有100个合格,不合格的有25个,这个零件的合格率是75%。( )
19.一个比例里,两个外项的积是1,则两个内项互为倒数。( )
20.所有的负数都比0小。( )
21.正方体的棱长扩大2倍,体积就扩大6倍。( )
四、计算题
22.直接写得数。
713+159= 605-378= 5.06×4= 32.8÷10=
0.68-0.32= 8×12.5%=
23.计算下面各题,怎样简便就怎样算。
276+476-276+52 44×80%×2.5×12.5
24.解方程。
(1) (2)∶x (3)0.2x+5%x=18
25.计算下面图形阴影部分的周长和面积。
五、解答题
26.张村有一块试验田种水稻,今年换种新品种后,产量是2600千克,今年产量比去年增产三成,去年的产量是多少千克?
27.甲乙两车分别从、两地同时相向而行,甲每小时行80千米,乙每小时行全程的,当乙行到全程的时,甲车再行全程的,可到达地。求、两地相距多少千米?
28.一个底面直径是10厘米、高是12厘米的圆柱形玻璃容器里装有一些水,水中浸没着一个底面直径是6厘米,高10厘米的圆锥形铁块,如果把铁块从水中取出,那么容器中水面高度将下降多少厘米?
29.港珠澳大桥是世界上最长的跨海大桥。主体工程连接桥梁和海底隧道的东、西人工岛。岛体结构采用深插式大直径钢圆筒和抛石斜坡堤组合结构。东人工岛使用钢圆筒59个,西人工岛使用钢圆筒61个。每个钢圆筒平均长度是55米。两个人工岛使用钢圆筒的总长度是多少米?
30.某物流公司将120吨货物运往一加工厂,如果要一次把所有货物全部运出,车辆的载重量与所需车辆的数量如下表。
载重量/吨 2.5 3 5 10
数量/辆 48 40 _____ _____
(1)将上表填写完整。
(2)车辆的载重量和所需车辆的数量成什么比例关系?为什么?
(3)如果用载重量为6吨的卡车来运,一共需要多少辆?
31.统计分析。
2021年下半年甲超市和乙超市销售盈利情况统计图
(1)下表是乙超市2021年下半年销售盈利情况统计结果。在统计图中画出乙超市的销售盈利情况。
时间/月 7 8 9 10 11 12
销售盈利/元 200 400 800 1200 1800 2000
(2)从上图中可以看出,2021年下半年甲超市的销售盈利情况呈( )趋势。乙超市的销售盈利情况呈( )趋势。(填“上升”或“下降”)
(3)9月份甲超市的销售盈利额度比乙超市多( )%。
参考答案:
1.A
【分析】根据数的组成,每一个数位上数字是几就表示有几个这样的计数单位,据此逐项分析即可。
【详解】A.1.60中的“6”在十分位上,表示6个十分之一;
B.1.06中的“6”在百分位上,表示6个百分之一;
C.1.006中的“6”在千分位上,表示6个千分之一;
D.60.1中的“6”在十位上,表示6个十。
故答案为:A
【点睛】解答本题的关键是掌握各个数位的计数单位。
2.B
【分析】小红计算14×12时,将12拆成10和2,分别将这两个数与14相乘,再将乘积加起来。
【详解】能表示她思考过程的图是。
故答案为:B。
【点睛】计算两位数乘两位数数,可以将其中一个两位数拆成整十数和一位数,分别求出这两个数与另一个两位数相乘,再将乘积加起来即可。
3.C
【分析】根据“总价=单价×数量”表示出购买8个足球和b个篮球各需要多少元,最后相加求和,据此解答。
【详解】购买8个足球的钱数:8a(元)
购买b个篮球的钱数:56b(元)
学校买足球和篮球的总钱数:(8a+56b)元
故答案为:C
【点睛】掌握单价、数量、总价之间的关系是解答题目的关键。
4.C
【分析】可能性的数值表示:通常概率用英文字母P来表示,记作:P(事件)。可能性的计算步骤:列出所有可能发生的结果,并判定每个结果发生的可能性都相等;再确定所有可能发生的结果个数n和其中出现所求事件的结果个数m;最后计算所求事件发生的可能性(概率),公式为:
分别算出甲、乙两个盘子小球停在黑色区域的可能性,分析可知黑色区域的可能性就是黑色占整个盘子的几分之几,再比较大小即可。
【详解】甲:将盘子平均分成6份,黑色区域是2份,则a=;
乙:将盘子平均分成9份,黑色区域是3份,则b=;
a=b
故答案为:C
5.D
【分析】确定观测点,判断被观测点区域,然后结合数据写出位置。
【详解】雷达站为观测点,是从雷达站观看鱼雷艇,根据上北下南,左西右东,鱼雷艇在东北区域,根据图形数据30°,鱼雷艇在雷达站东偏北30°方向或北偏东60°的方向。
故答案为:D
【点睛】此题考查用方位角表示位置,关键判断观测点与偏向角度数。
6.B
【分析】把这件毛衣的原价看作单位“1”,现价占原价的(1+10%)×(1-10%),假设出原价并求出这件毛衣的现价,最后比较大小,据此解答。
【详解】假设这件毛衣的原价为1。
1×(1+10%)×(1-10%)
=1.1×0.9
=0.99
因为0.99<1,所以现价比原价低。
故答案为:B
【点睛】第一个10%的单位“1”是商品的原价,第二个10%的单位“1”是商品提价10%后的价格,注意二者的区别。
7.C
【分析】根据图上距离∶实际距离=比例尺,据此解答即可。
【详解】5mm=0.5cm
25∶0.5=(25×4)∶(0.5×4)
=100∶2
=(100÷2)∶(2÷2)
=50∶1
故答案为:C
【点睛】本题考查比例尺,明确图上距离∶实际距离=比例尺是解题的关键。
8.C
【分析】等底等高的圆锥的体积是圆柱的,那么瓶中一半液体倒入杯中能倒满3杯,瓶中液体全倒入杯中,可以倒6杯。
【详解】由分析知:
令圆柱的高为2,则圆锥的高为1,瓶子底面和杯口面积相等等于S
则圆柱体积为:2S
圆锥的体积为:1×S
2S6(杯)
所以能倒满6杯。
故选:C
【点睛】此题考查了圆柱和圆锥的体积公式的灵活应用。
9. 120%x 7000 8万
【分析】将常规水稻产量看作单位“1”,从中国杂交水稻产量高出常规水稻20%左右,可以得出中国杂交水稻产量是常规水稻的(1+20%),求一个数的百分之几是多少,用乘法计算;70000000的计数单位是1,换算为“万”做单位,小数点移动4位即可求出答案;由1平方千米=100公顷,低级单位转变高级单位除以进率可以求出答案。
【详解】(1)x×(1+20%)
=x×120%
=120%x或1.2x
(2)70000000÷10000=7000,70000000=7000(万)
(3)800÷100=8,800万公顷=8万平方千米。
【点睛】此题考查求一个数多百分之几是多少与字母代表数的运用以及单位进率换算。
10.0、3、6、9
【分析】
2的倍数的数的特征是:个位上是0、2、4、6、8的数;3的倍数的数的特征是:各位上的数字之和是3的倍数,这个数就是3的倍数;5的倍数的数的特征是:个位上是0或5的数都是5的倍数;120个位上是0,所以已经满足同时能被2、5整除,所以只需要满足这个数是能被3整除即可;由此解答。
【详解】
120个位上的数是0,能同时被2、5整除;
1+2+0+0=3
1+2+3+0=6
1+2+6+0=9
1+2+9+0=12
填入0、3、6、9时,12能被3整除。
所以里填0、3、6、9,能同时被2、3、5整除。
【点睛】此题主要考查2、3、5的倍数的特征。
11. 8 2
【分析】将单位“1”平均分成若干份,表示其中这样一份的数为分数单位。
据此可知,的分数单位是,它含有8个这样的分数单位;
最小的质数是2,2-=。
所以再添上2个这样的分数单位就是最小的质数。
【详解】根据分数单位的意义可知,的分数单位是,它含有8个这样的分数单位;
最小的质数是2,2-=,所以再添上2个这样的分数单位就是最小的质数。
【点睛】求一个带分数含有多少个分数单位时,要先将这个带分数化为假分数。
12. 3 8
【分析】从x∶y=( )∶( )中可知:x是外项,y是内项;利用比例的基本性质:两外项的积等于两内项的积,则8是外项,3是内项;据此填空。
【详解】根据分析可知:
根据8x=3y组成一个比例x∶y=3∶8。
13.5
【分析】有4种水果,每个小朋友任意选择一种有4种选择方法,最差情况是4个小朋友选择的水果都不相同,此时只要再有一个小朋友任意选择一种水果,就能保证有两人选的水果是一样的,据此解答。
【详解】4+1=5(个)
所以,至少要有5个小朋友才能保证有两人选的水果是相同的。
【点睛】掌握抽屉原理的解题方法是解答题目的关键。
14.64
【分析】由圆的周长公式C=πd,得d=C÷2,由此求出圆的直径,而此圆是一个正方形内所画的一个最大的圆,所以圆的直径就是正方形的边长,再根据正方形的面积公式S=a×a,列式求出这个正方形的面积。
【详解】正方形的边长:25.12÷3.14=8(厘米)
正方形的面积:8×8=64(平方厘米)
【点睛】解答本题的关键是知道在一个正方形内所画最大圆的直径是正方形的边长,再灵活利用圆的周长公式与正方形的面积公式解决问题。
15.7.536
【分析】先求出5分钟从水管流出的水的长度,再利用圆柱的体积=底面积×高,即可求出浪费的水的体积。
【详解】5分钟=300秒
2厘米=0.2分米
8厘米=0.8分米
3.14×(0.2÷2)2×(0.8×300)
=3.14×2.4
=7.536(立方分米)
=7.536升
共浪费7.536升。
【点睛】本题重点考查学生对实际生活中数学问题转化为数学公式的能力,强化圆柱体积公式的实际应用。
16.16
【分析】根据题意表面积增加的部分为底是4分米,高也是4分米的两个三角形的面积,据此解答。
【详解】4×4÷2×2=16(平方分米),表面积增加16平方分米。
故答案为:16。
【点睛】解答此题的关键是明确圆锥沿底面直径切成两半,增加的是两个完全一样的三角形,并且三角形的底是圆锥的直径,高是圆锥的高。
17.×
【分析】根据三角形的三边关系:两边之和大于第三边,三角形的两边的差一定小于第三边;进行解答即可。
【详解】因为3+3=6,所以不能围成三角形;原题说法错误。
故答案为:×
【点睛】此题关键是根据三角形的三边关系进行分析、解答。
18.×
【分析】先理解合格率,合格率是指合格的零件个数占零件总个数的百分之几,计算方法为:合格零件数÷零件总个数×100%=合格率,由此代入数据列式解答。
【详解】100÷(100+25)×100%
=100÷125×100%
=80%
故原题干说法错误。
【点睛】此题属于典型的百分率问题,都是用一部分数量(或全部数量)除以全部数量乘百分之百,计算时一定要找准对应量。
19.√
【分析】根据比例的基本性质:两外项之积等于两内项之积,可以知道两个内项的积也是1,再根据倒数的定义:乘积是1的两个数互为倒数进行判断。
【详解】两个外项的积是1,那么两个内项的积也是1,乘积为1的两个数互为倒数,所以两个内项互为倒数,原题说法正确。
故答案为:√
【点睛】熟练掌握比例的基本性质和倒数的意义是解答本题的关键。
20.√
【分析】根据负数的认识,比0小的数叫负数,进行分析。
【详解】所有的负数都比0小,说法正确。
故答案为:√
【点睛】0是正数和负数的分界点,0不是正数也不是负数。
21.×
【分析】设原来的棱长是1,棱长扩大2倍后是2,分别计算体积,然后确定体积扩大的倍数,再进行判断。
【详解】设原来的棱长是1,棱长扩大2倍后是2;
对比发现,体积扩大8倍,故题干阐述错误
故答案为:×。
【点睛】正方体的棱长扩大2倍,棱长和扩大2倍,表面积扩大4倍,体积扩大8倍。
22.872;227;20.24;3.28;
;0.36;1;
【详解】略
23.528;1100;
【分析】(1)按照加法交换律和结合律计算;
(2)按乘法交换律和结合律计算;
(3)先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的乘法。
【详解】(1)276+476-276+52
=(276-276)+(476+52)
=0+528
=528
(2)44×80%×2.5×12.5
=(44×2.5)×(80%×12.5)
=(11×4×2.5)×10
=110×10
=1100
(3)×[(-)÷]
=×[(÷]
=×
=
24.(1)y=1.65;(2)x=;(3)x=72
【分析】(1)根据比例的基本性质,把比例化为方程,两边再同时除以3;
(2)根据比例的基本性质,把比例化为方程,两边再同时乘;
(3)先把方程左边化简为0.25x,两边再同时乘4。
【详解】(1)
解:3y=1.1×4.5
3y÷3=1.1×4.5÷3
y=1.65
(2)∶x
解:x=
x=
x=
(3)0.2x+5%x=18
解:0.25x=18
4×0.25x=18×4
x=72
25.周长48.56dm,面积78.88dm2
【分析】观察图形可得:阴影部分的周长=直径是8dm的圆的周长+10dm的边长×2+16dm的边长,然后再根据圆的周长公式C=πd进行解答;
阴影部分的面积=上底为10dm、下底为16dm、高为8dm的梯形的面积-直径是8dm的半圆的面积,然后再根据梯形的面积公式S=(a+b)h÷2,圆的面积公式S=πr2进行解答。
【详解】×3.14×8+10×2+16
=12.56+36
=48.56(dm)
(10+16)×8÷2-3.14×(8÷2)2÷2
=104-25.12
=78.88(dm2)
26.2000千克
【分析】根据条件“ 今年换种新品种后,产量是2600千克,今年产量比去年增产三成 ”可知,去年的产量×(1+30%)=今年的产量,已知今年的产量,要求去年的产量,用除法计算,据此列式解答。
【详解】三成=30%;
2600÷(1+30%)
=2600÷1.3
=2000(千克)
答:去年的产量是2000千克。
【点睛】此题主要考查了成数的应用,明确去年产量和今年产量的关系是解答本题的关键。
27.600千米
【分析】根据题意,把两地之间的路程看作单位“1”,已知甲每小时行80千米,乙每小时行全程的,当乙行到全程的时,甲车再行全程的,也就是乙行到全程的时,甲行了全程的;根据在相同时间内,所行路程的比等于速度的比,由此求出甲乙速度的比是:(1-)∶=4∶3,已知甲每小时行80千米,这样就可以求出乙的速度,根据已知一个数的百分之几是多少,求这个数,用除法解答即可。
【详解】甲乙速度比是:(1-)∶=4∶3
所以乙车每小时的速度是:
(千米)
两地相距:
(千米)
答:、两地相距600千米。
【点睛】解答此题关键是把两地之间的路程看作单位“1”,求出甲乙速度的比,由甲每小时行80千米,就可以求出乙的速度,由此解决问题。
28.1.2厘米
【分析】根据题意可知,把圆锥形铁块从圆柱形玻璃容器中取出后,水面下降的高等于圆锥的体积除以圆柱的底面积。根据圆锥的体积公式:,圆的面积公式:,代入数据进行解答即可。
【详解】×3.14×(6÷2)2×10÷[3.14×(10÷2)2]
=×3.14×9×10÷[3.14×25]
=×28.26×10÷78.5
=9.42×10÷78.5
=94.2÷78.5
=1.2(厘米)
答:容器中水面高度将下降1.2厘米。
【点睛】此题主要考查圆柱、圆锥体积公式的灵活运用,圆的面积公式及应用,关键是熟记公式。
29.6600米
【分析】要求两个人工岛使用钢圆筒的总长度是多少米,先分别计算出两个人工岛使用的钢圆筒的长度,再相加即可。
【详解】59×55=3245(米)
61×55=3355(米)
3245+3355=6600(米)
答:两个人工岛使用钢圆筒的总长度是6600米。
【点睛】本题考查乘法在实际中的应用,弄清题目中的数量关系是关键。
30.(1)24;12
(2)反比例;见详解
(3)20辆
【分析】(1)已知货物总吨数是120吨,根据所需的车辆数量=货物的总吨数÷车辆的载重量,即可求出统计表中载重量是5吨、10吨时所需的车辆数量,进而把表格填完整。
(2)判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例。
(3)用货物的总吨数除以车辆的载重量,即可求出所需车辆的数量。
【详解】(1)120÷5=24(辆)
120÷10=12(辆)
如下表:
载重量/吨 2.5 3 5 10
数量/辆 48 40 24 12
(2)2.5×48=3×40=5×24=10×12=120(一定)
乘积一定,车辆的载重量与所需车辆的数量成反比例关系。
(3)120÷6=20(辆)
答:一共需要20辆。
【点睛】本题考查正、反比例的意义及辨识方法,同时能运用统计表中提供的信息解决问题。
31.(1)见详解
(2)下降;上升
(3)112.5%
【分析】(1)观察折线统计图,横轴代表时间,纵轴代表销售盈利,然后根据统计表在统计图中标出相应的点,然后顺次连接即可;
(2)根据折线统计图中两条线的变化趋势填空即可;
(3)先求出9月份甲超市的销售盈利额度比乙超市多多少,再除以乙超市9月份销售盈利额度即可。
【详解】(1)如图所示:
(2)2021年下半年甲超市的销售盈利情况呈下降趋势。乙超市的销售盈利情况呈上升趋势。
(3)(1700-800)÷800
=900÷800
=112.5%
9月份甲超市的销售盈利额度比乙超市多112.5%。
【点睛】本题考查求一个数比另一个数多百分之几,明确单位“1”是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
