数学:15.1 全等三角形课件(沪科版八年级上)
文档属性
| 名称 | 数学:15.1 全等三角形课件(沪科版八年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 29.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-26 00:00:00 | ||
图片预览



文档简介
课件15张PPT。课题:全等三角形(复习课)
授课人:程飞虎
(1)全等三角形有哪些判定方法?
(2)判定两个直角三角形全等有哪些方法?
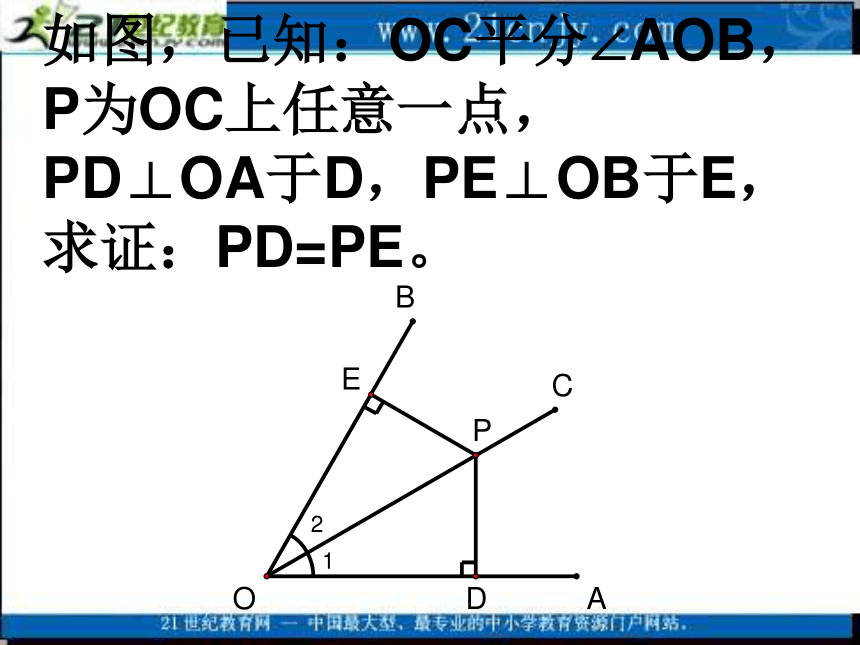
(3)全等三角形有哪些性质?例1、求证:角平分线上的点到角两边的距相等。如图,已知:OC平分∠AOB,
P为OC上任意一点,
PD⊥OA于D,PE⊥OB于E,
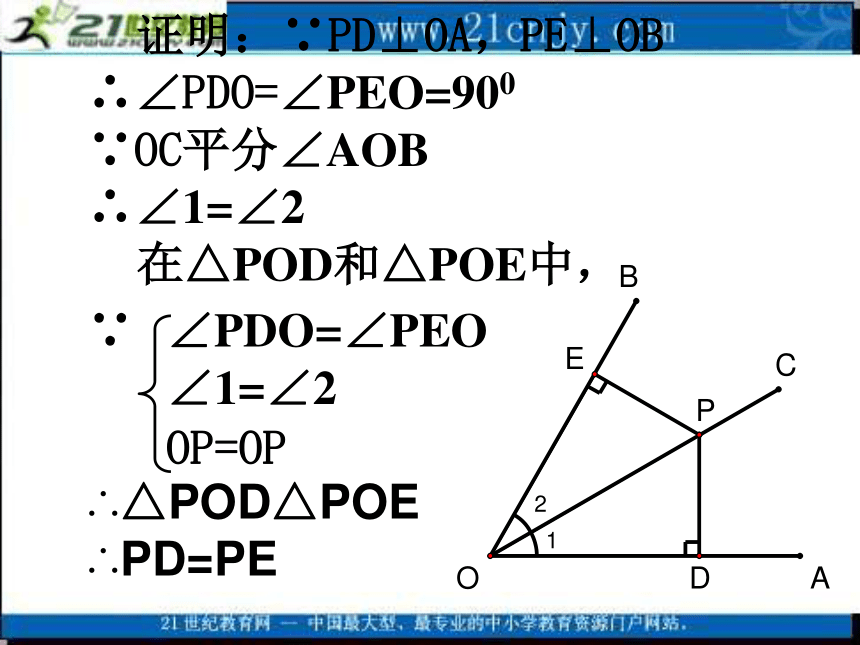
求证:PD=PE。证明:∵PD⊥OA,PE⊥OB ∴∠PDO=∠PEO=900 ∵OC平分∠AOB ∴∠1=∠2
在△POD和△POE中,
∵ ∠PDO=∠PEO
∠1=∠2
OP=OP
∴△POD△POE
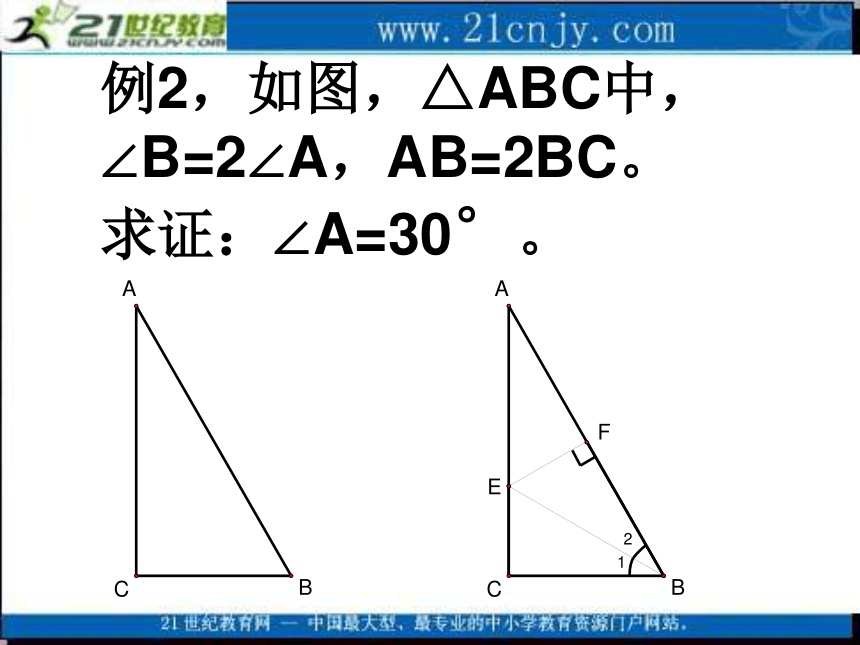
∴PD=PE例2,如图,△ABC中,
∠B=2∠A,AB=2BC。
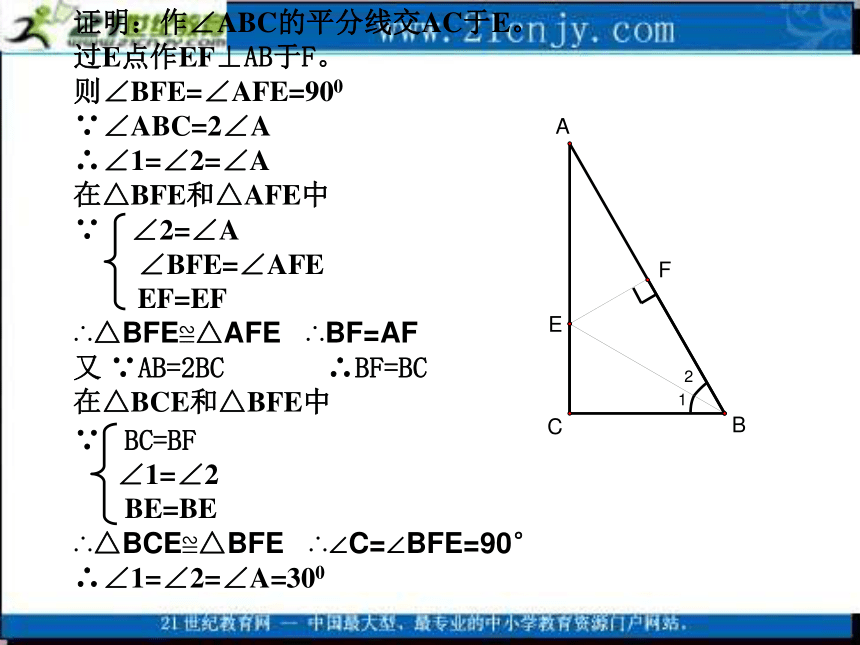
求证:∠A=30°。证明:作∠ABC的平分线交AC于E。
过E点作EF⊥AB于F。
则∠BFE=∠AFE=900
∵∠ABC=2∠A
∴∠1=∠2=∠A
在△BFE和△AFE中
∵ ∠2=∠A
∠BFE=∠AFE
EF=EF
∴△BFE≌△AFE ∴BF=AF
又 ∵AB=2BC ∴BF=BC
在△BCE和△BFE中
∵ BC=BF
∠1=∠2
BE=BE
∴△BCE≌△BFE ∴∠C=∠BFE=90°
∴∠1=∠2=∠A=300例3,如图,△ABC中,∠A=60°,
两条角平分线BD、CE相交于点O,
求证:OD=OE。证明:在BC上取一点F,
使BF=BE,连结OF。
在△BOE和△BOF中
∵ BE=BF
∠1=∠2
BO=BO
∴△BOE≌△BOF ∴OE=OF,∠5=∠6
∵∠A=600 ∴∠2+∠4=(1800—600)÷2=600
∴∠BOC=1800—600=1200 ∴∠5=600
∴∠6=∠5=∠8=∠7=600
在△COF和△COD中,
∵ ∠3=∠4
CO=CO
∠7=∠8
∵△COF≌△COD
∴OF=OD
∴OD=OE例4、如图,△ABC中,AB=AC,
∠A=100°,∠B的平分线
交AC于E,求证:BC=AE+EB证明:在BC上截取BD=BE,
连结ED。在BD上截取
BF=BA,连结FE。
∵∠A=100°,AB=AC,BE平分∠ABC,
∴∠1=∠2=20°
又∵BE=BE
∴△ABE≌△FBE
∴∠3=∠A=100°,AE=EF
∴∠4=80°
∵BE=BD,∠2=20°,
∴∠5=80°
∴∠4=∠5 ∴EF-=ED ∴AE=ED
又∵∠C=40°
∴∠5=80 ° ∴∠6=40 °
∴DE=DC
∴AE=DC
∴BC=BD+DC=BE+AE
即BC=AE+EB思考题:如图,已知:△ABC中 , AB﹥AC,AD平分∠BAC,P是AD上任意一点。
求证:AB-AC ﹥ PB-PC。证明:∵AB>AC,在AB上截取AE=AC,连结PE,
∵ AD平分∠BAC,∴∠1=∠2
在△APE和△APC中,
AE=AC
∵ ∠1=∠2
AP=AP
∴△APE≌△APC∴PE=PC
在△PBE中,PB-PE<BE
∴AB-AC ﹥ PB-PC
角平分线 构造翻折全等。小结作业 :预习下一章
(1)全等三角形有哪些判定方法?
(2)判定两个直角三角形全等有哪些方法?
(3)全等三角形有哪些性质?例1、求证:角平分线上的点到角两边的距相等。如图,已知:OC平分∠AOB,
P为OC上任意一点,
PD⊥OA于D,PE⊥OB于E,
求证:PD=PE。证明:∵PD⊥OA,PE⊥OB ∴∠PDO=∠PEO=900 ∵OC平分∠AOB ∴∠1=∠2
在△POD和△POE中,
∵ ∠PDO=∠PEO
∠1=∠2
OP=OP
∴△POD△POE
∴PD=PE例2,如图,△ABC中,
∠B=2∠A,AB=2BC。
求证:∠A=30°。证明:作∠ABC的平分线交AC于E。
过E点作EF⊥AB于F。
则∠BFE=∠AFE=900
∵∠ABC=2∠A
∴∠1=∠2=∠A
在△BFE和△AFE中
∵ ∠2=∠A
∠BFE=∠AFE
EF=EF
∴△BFE≌△AFE ∴BF=AF
又 ∵AB=2BC ∴BF=BC
在△BCE和△BFE中
∵ BC=BF
∠1=∠2
BE=BE
∴△BCE≌△BFE ∴∠C=∠BFE=90°
∴∠1=∠2=∠A=300例3,如图,△ABC中,∠A=60°,
两条角平分线BD、CE相交于点O,
求证:OD=OE。证明:在BC上取一点F,
使BF=BE,连结OF。
在△BOE和△BOF中
∵ BE=BF
∠1=∠2
BO=BO
∴△BOE≌△BOF ∴OE=OF,∠5=∠6
∵∠A=600 ∴∠2+∠4=(1800—600)÷2=600
∴∠BOC=1800—600=1200 ∴∠5=600
∴∠6=∠5=∠8=∠7=600
在△COF和△COD中,
∵ ∠3=∠4
CO=CO
∠7=∠8
∵△COF≌△COD
∴OF=OD
∴OD=OE例4、如图,△ABC中,AB=AC,
∠A=100°,∠B的平分线
交AC于E,求证:BC=AE+EB证明:在BC上截取BD=BE,
连结ED。在BD上截取
BF=BA,连结FE。
∵∠A=100°,AB=AC,BE平分∠ABC,
∴∠1=∠2=20°
又∵BE=BE
∴△ABE≌△FBE
∴∠3=∠A=100°,AE=EF
∴∠4=80°
∵BE=BD,∠2=20°,
∴∠5=80°
∴∠4=∠5 ∴EF-=ED ∴AE=ED
又∵∠C=40°
∴∠5=80 ° ∴∠6=40 °
∴DE=DC
∴AE=DC
∴BC=BD+DC=BE+AE
即BC=AE+EB思考题:如图,已知:△ABC中 , AB﹥AC,AD平分∠BAC,P是AD上任意一点。
求证:AB-AC ﹥ PB-PC。证明:∵AB>AC,在AB上截取AE=AC,连结PE,
∵ AD平分∠BAC,∴∠1=∠2
在△APE和△APC中,
AE=AC
∵ ∠1=∠2
AP=AP
∴△APE≌△APC∴PE=PC
在△PBE中,PB-PE<BE
∴AB-AC ﹥ PB-PC
角平分线 构造翻折全等。小结作业 :预习下一章
