§1.2 直线的方程(1)
图片预览




文档简介
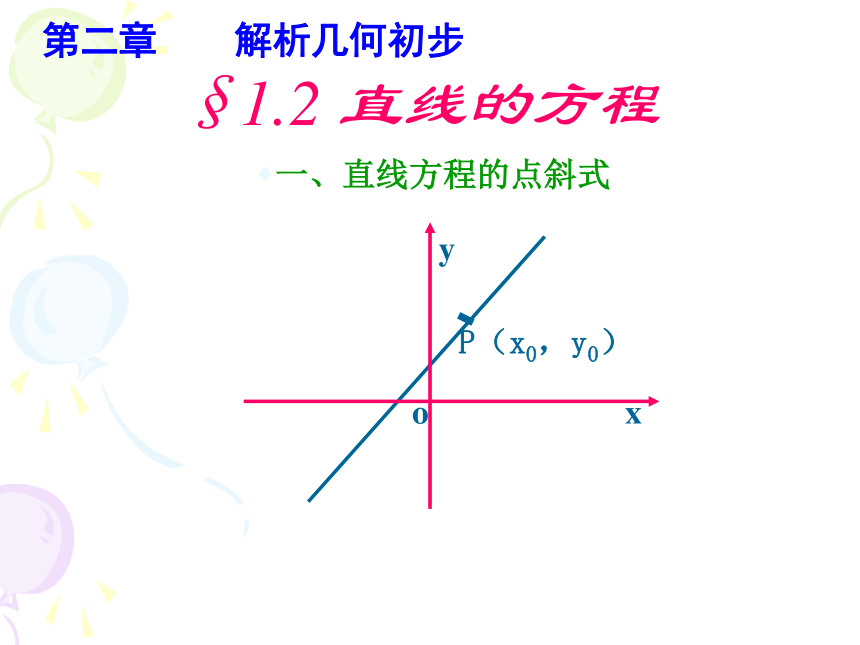
课件16张PPT。§1.2 直线的方程一、直线方程的点斜式P(x0,y0)o第二章 解析几何初步复习:一、平面直角坐标系内确定一条直线的几何要素。 第二章 解析几何初步思考1:已知直线过点P(0,3),且斜率k =2 ,那么,我们该如何将直线l 上任意点的坐标(x,y)满足的关系表示出来?得方程:y=2x+3 。
这个方程就是所求的直线上所有点的坐标(x,y)满足的关系式。小结:
1.直线l上任一点的坐标(x,y)都满足y=2x+3。
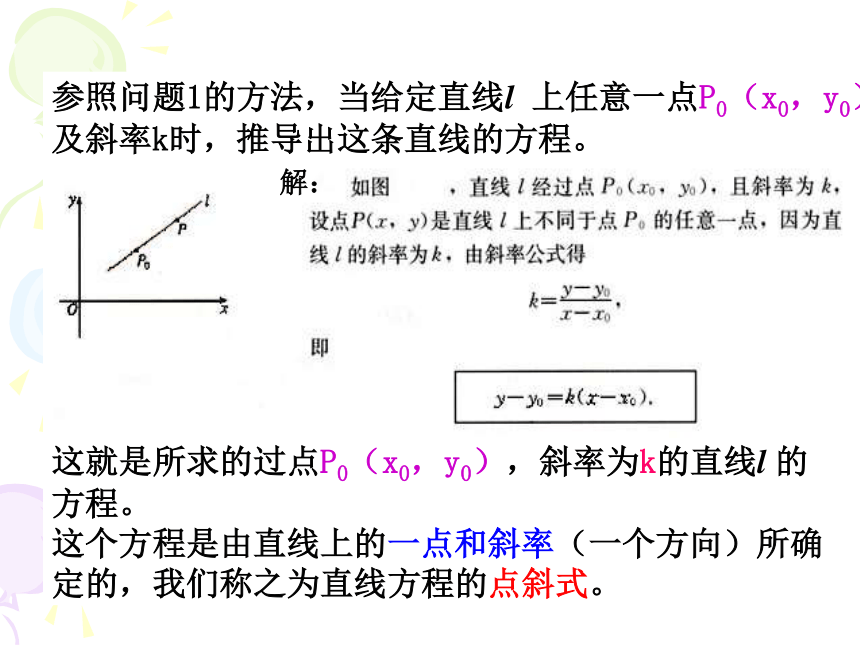
2.满足方程y=2x+3的每一个数对(x,y)所对应的点都在直线l上。抽象概括:一般地,如果一条直线l 上任一点的坐标(x,y)都满足一个方程,满足该方程的每一个数对(x,y)所确定的点都在直线l上,我们把这个方程称为直线l 的方程。这就是所求的过点P0(x0,y0),斜率为k的直线l 的方程。
这个方程是由直线上的一点和斜率(一个方向)所确定的,我们称之为直线方程的点斜式。参照问题1的方法,当给定直线l 上任意一点P0(x0,y0)及斜率k时,推导出这条直线的方程。练习4:
直线l 经过点P0(-2,3),且倾斜角a=450,求直线l 的点斜式方程,并画出直线l 。解:直线l 经过点P0(-2,3),斜率 k=tan 45°=1,代入点斜式方程得:
y-3=x+2,
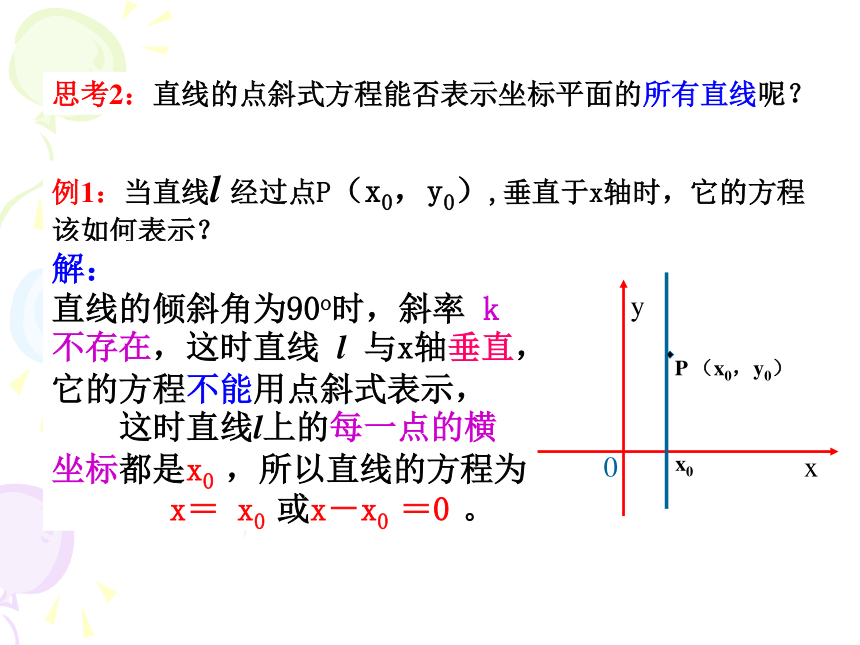
即 y=x-1。画图时,只需再找出直线l 上的另一点P1(x1,y1),如P1(-1,4),过P0 ,P1的直线即为所求,如右图。思考2:直线的点斜式方程能否表示坐标平面的所有直线呢?例1:当直线l 经过点P(x0,y0),垂直于x轴时,它的方程该如何表示?解:
直线的倾斜角为90o时,斜率 k不存在,这时直线 l 与x轴垂直,
它的方程不能用点斜式表示,
这时直线l上的每一点的横坐标都是x0 ,所以直线的方程为
x= x0 或x-x0 =0 。例2:解:
直线的斜率为 k=tan 0o =0,这时直线l 与x轴平行,方程为:当直线l 经过点P(x0,y0),倾斜角为0o时,求该直线的方程。练习3:
求经过点(0,b),斜率是k的直线方程。我们把直线l 与y轴交点
(0,b)的纵坐标叫做直线l 在y轴上的截距。方程y=kx+b由直线的斜率k与它在y轴上的截距b确定,思考4:直线l 在x轴上的截距是什么呢?思考5:
观察方程y=kx+b,它的形式具有什么特点?1、左端y的系数恒为1.
2、右端x的系数k和常数项b具有明显得几何意义:
k是直线的斜率,
b是直线l 在y轴上的截距.练习5:
求经过两点A(-5,0),B(3,-3)的直线方程。小结:
1、直线 l 的方程
2、直线方程的点斜式(重点)
y- y0 = k(x-x0)
3、直线方程的截距式
y=kx+b思考6:
方程y=kx+b的形式与一次函数解析式类似,那么,在一次函数y=kx+b中,k和b的几何意义又是什么呢?方程y=kx+b,它的形式具有的特点:1、左端y的系数恒为1.
2、右端x的系数k和常数项b具有明显得几何意义:
k是直线的斜率,
b是直线l 在y轴上的截距.思考6:
方程y=kx+b的形式与一次函数解析式类似,那么,在一次函数y=kx+b中,k和b的几何意义又是什么呢?再见作业:
P80 2,3We have joy ,we have fun ,we have season in the sun , but the wine and the song like the season。xyQ(x,y)P(0,3)l0解:
由于这条直线经过点(0,b)并且斜率是k,所以,它的点斜式方程是
y-b=k(x-0),
可化为 y=kx+b。解: 如右图,直线l 过点P(0,3),斜率为k=2,点Q(x,y)是直线l上不同于P 的任意一点。由于P,Q都在l上,所以:直线l的斜率为:
这个方程就是所求的直线上所有点的坐标(x,y)满足的关系式。小结:
1.直线l上任一点的坐标(x,y)都满足y=2x+3。
2.满足方程y=2x+3的每一个数对(x,y)所对应的点都在直线l上。抽象概括:一般地,如果一条直线l 上任一点的坐标(x,y)都满足一个方程,满足该方程的每一个数对(x,y)所确定的点都在直线l上,我们把这个方程称为直线l 的方程。这就是所求的过点P0(x0,y0),斜率为k的直线l 的方程。
这个方程是由直线上的一点和斜率(一个方向)所确定的,我们称之为直线方程的点斜式。参照问题1的方法,当给定直线l 上任意一点P0(x0,y0)及斜率k时,推导出这条直线的方程。练习4:
直线l 经过点P0(-2,3),且倾斜角a=450,求直线l 的点斜式方程,并画出直线l 。解:直线l 经过点P0(-2,3),斜率 k=tan 45°=1,代入点斜式方程得:
y-3=x+2,
即 y=x-1。画图时,只需再找出直线l 上的另一点P1(x1,y1),如P1(-1,4),过P0 ,P1的直线即为所求,如右图。思考2:直线的点斜式方程能否表示坐标平面的所有直线呢?例1:当直线l 经过点P(x0,y0),垂直于x轴时,它的方程该如何表示?解:
直线的倾斜角为90o时,斜率 k不存在,这时直线 l 与x轴垂直,
它的方程不能用点斜式表示,
这时直线l上的每一点的横坐标都是x0 ,所以直线的方程为
x= x0 或x-x0 =0 。例2:解:
直线的斜率为 k=tan 0o =0,这时直线l 与x轴平行,方程为:当直线l 经过点P(x0,y0),倾斜角为0o时,求该直线的方程。练习3:
求经过点(0,b),斜率是k的直线方程。我们把直线l 与y轴交点
(0,b)的纵坐标叫做直线l 在y轴上的截距。方程y=kx+b由直线的斜率k与它在y轴上的截距b确定,思考4:直线l 在x轴上的截距是什么呢?思考5:
观察方程y=kx+b,它的形式具有什么特点?1、左端y的系数恒为1.
2、右端x的系数k和常数项b具有明显得几何意义:
k是直线的斜率,
b是直线l 在y轴上的截距.练习5:
求经过两点A(-5,0),B(3,-3)的直线方程。小结:
1、直线 l 的方程
2、直线方程的点斜式(重点)
y- y0 = k(x-x0)
3、直线方程的截距式
y=kx+b思考6:
方程y=kx+b的形式与一次函数解析式类似,那么,在一次函数y=kx+b中,k和b的几何意义又是什么呢?方程y=kx+b,它的形式具有的特点:1、左端y的系数恒为1.
2、右端x的系数k和常数项b具有明显得几何意义:
k是直线的斜率,
b是直线l 在y轴上的截距.思考6:
方程y=kx+b的形式与一次函数解析式类似,那么,在一次函数y=kx+b中,k和b的几何意义又是什么呢?再见作业:
P80 2,3We have joy ,we have fun ,we have season in the sun , but the wine and the song like the season。xyQ(x,y)P(0,3)l0解:
由于这条直线经过点(0,b)并且斜率是k,所以,它的点斜式方程是
y-b=k(x-0),
可化为 y=kx+b。解: 如右图,直线l 过点P(0,3),斜率为k=2,点Q(x,y)是直线l上不同于P 的任意一点。由于P,Q都在l上,所以:直线l的斜率为:
