福建省百校2024届高三上学期期中联考数学试卷(含解析)
文档属性
| 名称 | 福建省百校2024届高三上学期期中联考数学试卷(含解析) | 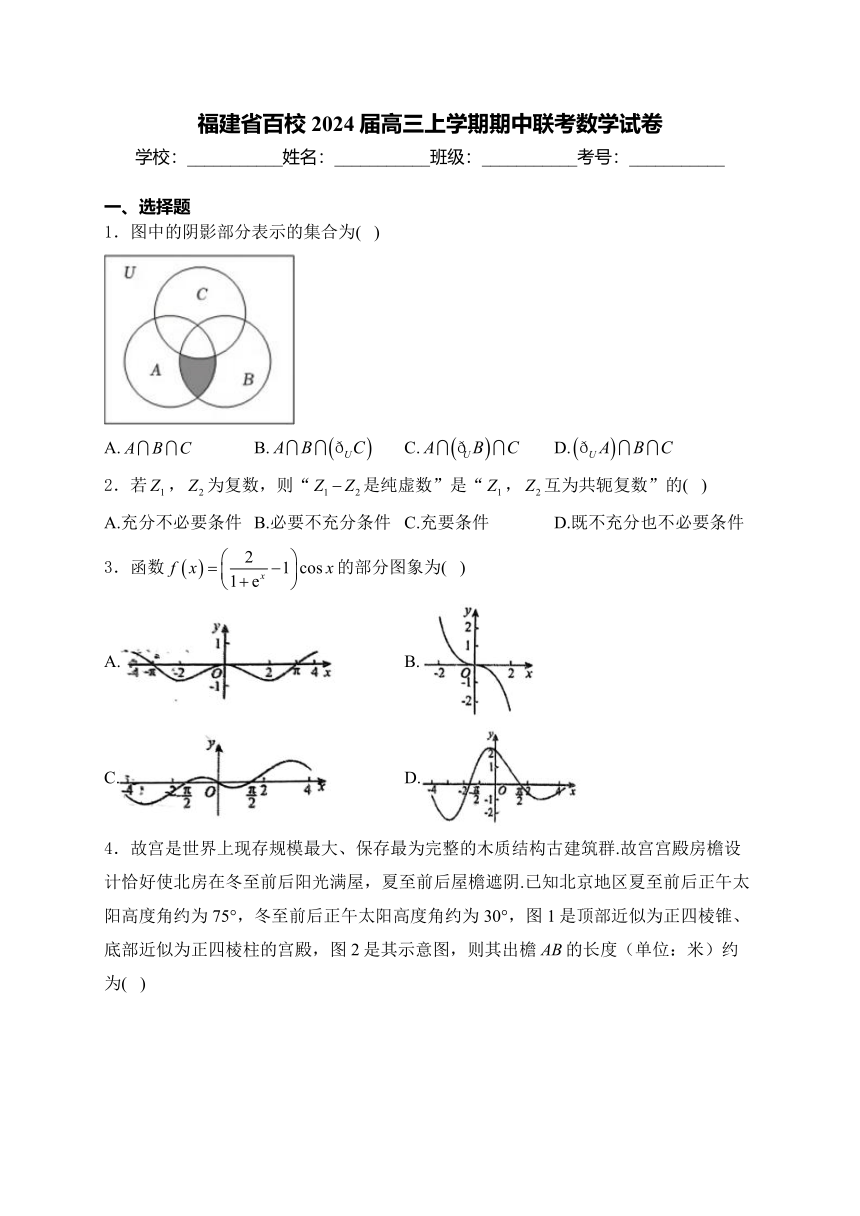 | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-28 07:22:17 | ||
图片预览





文档简介
福建省百校2024届高三上学期期中联考数学试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.图中的阴影部分表示的集合为( )
A. B. C. D.
2.若,为复数,则“是纯虚数”是“,互为共轭复数”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.函数的部分图象为( )
A. B.
C. D.
4.故宫是世界上现存规模最大、保存最为完整的木质结构古建筑群.故宫宫殿房檐设计恰好使北房在冬至前后阳光满屋,夏至前后屋檐遮阴.已知北京地区夏至前后正午太阳高度角约为75°,冬至前后正午太阳高度角约为30°,图1是顶部近似为正四棱锥、底部近似为正四棱柱的宫殿,图2是其示意图,则其出檐AB的长度(单位:米)约为( )
A.3 B.4 C. D.
5.已知数列满足,且,若,则正整数k为( )
A.13 B.12 C.11 D.10
6.如图,AB是圆O的一条直径,且.C,D是圆O上的任意两点,.点P在线段CD上,则的取值范围是( )
A. B. C. D.
7.已知直线,是函数图像相邻的两条对称轴,将的图像向右平移个单位长度后,得到函数的图像.若在上恰有三个不同的零点,则实数m的取值范围为( )
A. B. C. D.
8.已知,,,则( )
A. B. C. D.
二、多项选择题
9.设正实数a,b满足,则下列说法正确的是( )
A.的最小值为3 B.ab的最大值为1
C.的最小值为2 D.的最小值为2
10.函数的部分图象如图中实线所示,图中圆C与的图象交于M,N两点,且M在y轴上,则( )
A.函数在上单调递增
B.圆的半径为
C.函数的图象关于点成中心对称
D.函数在上单调递减
11.如图,在长方体中,E,F分别是棱,的中点,点P在侧面内,且,,则三棱锥外接球表面积的取值可能是( )
A. B. C. D.
12.已知数列满足,,则下列说法正确的有( )
A. B.
C.若,则 D.
三、填空题
13.已知,且,则______.
14.已知非零向量,满足,,若,则向量在向量方向上的投影向量的坐标为______.
15.已知数列满足,,若数列为单调递增数列,则的取值范围为______.
四、双空题
16.法国的拿破仑提出过一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个等边三角形的外接圆圆心恰好是一个等边三角形的三个顶点.”在ABC中,,以AB,BC,AC为边向外作三个等边三角形,其外接圆圆心依次为,,,则______;若的面积为,则三角形中的最大值为______.
五、解答题
17.已知函数,将的图象向左平移个单位长度,所得函数的图象关于y轴对称.
(1)求函数的解析式;
(2)若关于x的方程在上恰有两个实数根,求实数a的取值范围.
18.已知函数.
(1)讨论函数的单调性;
(2)若,是否存在整数,都有恒成立,若存在求出实数m的最小值,若不存在说明理由.
19.设数列前n项和满足,.
(1)证明:数列为等比数列;
(2)记,求数列的前n项和.
20.如图,在四棱锥中,PAD为等边三角形,M为PA的中点,,平面平面ABCD.
(1)证明:平面平面PAB;
(2)若,,,直线PB与平面MCD所成角的正弦值为,求三棱锥的体积.
21.如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数,的图像,图像的最高点为.边界的中间部分为长1千米的直线段CD,且,游乐场的后一部分边界是以O为圆心的一段圆弧DE.
(1)求曲线段FGBC的函数表达式;
(2)曲线段FGBC上的入口G距海岸线EF最近距离为1千米,现准备从入口G修一条笔直的景观路到O,求景观路GO长;
(3)如图,在扇形ODE区域内建一个平行四边形休闲区OMPQ,平行四边形的一边在海岸线EF上,一边在半径OD上,另外一个顶点P在圆弧DE上,且,求平行四边形休闲区OMPQ面积的最大值及此时的值.
22.已知函数.
(1)求在的单调区间与最值;
(2)当时,若,证明:有且仅有两个零点.
参考答案
1.答案:B
解析:由已知中阴影部分所表示的集合元素满足“是B的元素,也是A的元素,不是C的元素”,故阴影部分所表示的集合是.故选:B.
2.答案:D
解析:先验证充分性:令,满足是纯虚数,
但是不满足,互为共轨复数,所以充分性不成立;
再验证必要性:令,满足,互为共轭复数,
但是不满足是纯虚数,所以必要性不成立,
所以“是纯虚数”是“,互为共轭复数”的既不充分也不必要条件.
故选:D.
3.答案:C
解析:
,定义域为R,
为奇函数,故图象关于原点对称,故排除A,D;
令,则,,故有无数个零点,故排除B.
故选:C.
4.答案:C
解析:如图:由题意可得
,,
中,由正弦定理可得
直角三角形中,
的长度为米,
故选:C.
5.答案:B
解析:由已知可得
,,,,
以上各式累加可得,
又,代入
,即
,解得,
故,
令,解得.
故选:B.
6.答案:D
解析:如图,O为圆心,连接,
则
因为点P在线段上且,则圆心到直线的距离,
所以,
所以,则,
即的取值范围是.
故选:D.
7.答案:A
解析:由题意可知的最小正周期为,所以,所以,则,故,令,解得,由图像可知解得.
故选A项.
8.答案:A
解析:下面先证明,(且).
记,则
,
令,得:;
令,得:;
函数在上单增,在上单减,所以对任意,都有,即恒成立,所以对任意且,都有,即恒成立,故,故,
构造函数,则
故当时,单调递增,
故,即,
综上.
故选:A.
9.答案:ABD
解析:
10.答案:CD
解析:根据函数的图象以及圆C的对称性,
可得M,N两点关于圆心对称,
所以,于是
,
由及,得
由于,所以,
所以,,从而,故半径为
,故B错误;
当时,,,因为在区间
上先减后培,所以原函数在上先减后增,故A错误;
,故C正确;
当时,,即
,此时为减函数,故D正确.
故选:CD.
11.答案:BCD
解析:如图,连接,,,易证四边形是平行四边形,
则点在线段上,取的中点G,连接,,
分别取,的中点,,连接,
易知三棱锥外接球的球心O在直线上,连接,,,,
设三棱锥外接球的半径为R,则,
因为,所以,,
所以,所以.
则当P与E重合时,
此时三棱锥外接球的半径取得最小值;
当P与重合时,
此时三棱锥外接球的半径取得最大值,
故三棱锥外接球表面积的取值范围是.
12.答案:BCD
解析:对于A:,,
,
,故A错误;
对于B:,
要证,
则证,
即证,
即证,
令,则,,
设,
,
当时,,函数单调递增,
当时,,函数单调递减,
,
恒成立,
,故B正确;
易知足遂增数列,所以,
则,
,
则,即
所以,
即,
所以,
所以
而当时,则有,
故C正确;
令函数,
则
所以在上单调递减,
所以当时,,
则,
所以
,
所以,D正确.
故选:BCD.
13.答案:
解析:因为,所以
故,
所以.
故答案为:.
14.答案:
解析:
15.答案:
解析:由题意可得时,,
当时,,即,对也成立,
则,,
,
若数列为单调道壇数列,则恒成立,
即
化为对恒成立.
设,则
当时,,
当时,为递减数列,即
可得为最大值,且为,
则.故答寀为:.
16.答案:,4
解析:
17.答案:(1);
(2)
解析:(1),
将函数的图象向左平移个单位长度后,
所得函数为,
,,,.
又,,.
(2),,
当,即时,单调递增;
当,即时,单调递减.
且,,.
方程在上恰有两个实数根,
,实数a的取值范围为.
18.答案:(1)单调性见解析;
(2)3
解析:(1),,
当,,在单调递增,
当时,,
令,得,得,
在单调递增,在单调递减.
综上,时,在单调递增;
当时,在单调递增,在单调递减.
(2),,
,,
令,,
令,,在单调递减.
,
,使得,即,,
当,,,单调递增,
当,,,单调递减,
,
,,,m的最小值为3.
19.答案:(1)证明见解析;
(2)
解析:(1)证明:,且,
,
,,
令,可得,,
所以数列是首项为,公比为的等比数列.
(2)由(1)可得,
,,
,
.
20.答案:(1)证明见解析;
(2)
解析:(1)取AD中点为N,连接PN,
因为PAD为等边三角形,所以,
且平面平面ABCD,平面平面,面PAD,
所以平面ABCD,
又平面ABCD,所以,
又因为,,平面PAD,
所以平面PAD,
又因为平面PAD,所以,
因为M为AP中点,所以,且,平面PAD,
所以平面PAB,且平面CDM,
所以平面平面PAB.
(2)由(1)可知,且,,
所以平面PAD,且平面PAD,所以,
以A为坐标原点,分别以AB,AD所在直线为x,y轴,建立如图所示空间直角坐标系,
设,则可得
,,,,,,
即,,,
设平面MCD的法向量为,
则
则可得,取,则,,
所以平面MCD的一个法向量为,
设直线PB与平面MCD所成角为,
所以,
解得,或,即(舍去)或1,
所以,.
21.答案:(1),;
(2)千米;
(3)时,平行四边形面积最大值为
解析:(1)由已知条件,得,
又,,.
又当时,有,,
曲线段FBC的解析式为,.
(2)由得,
又,,,,,
景观路GO长为千米.
(3)如图,,,,,
作轴于点,在中,,
在中,,
,
,
当时,即时,平行四边形面积最大值为.
22.答案:(1)的增区间为:,,减区间为:,;的最大值为,最小值为;
(2)证明见解析.
解析:(1),
解得或0或,
与的分布列如下:
x 0
+ - + -
↑ 极大值 ↓ 极小值1 ↑ 极大值 ↓
所以,的增区间为:,,减区间为:,,
的最大值为,最小值为.
(2)的定义域为R,
,
所以为偶函数.
,当时,有且仅有两个零点
当时,在上有且仅有一个零点.
,
当时,若,则,所以在上单调递减,
,在上有且仅有一个零点;
当时,存在,使得,
当时,,
当时,,
当时,,
所以,在递增,在上递减,
在上单调递增,
,,可得,
当时,,
所以,
所以,在上有且仅有一个零点,综上,当时,有且仅有两个零点.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.图中的阴影部分表示的集合为( )
A. B. C. D.
2.若,为复数,则“是纯虚数”是“,互为共轭复数”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.函数的部分图象为( )
A. B.
C. D.
4.故宫是世界上现存规模最大、保存最为完整的木质结构古建筑群.故宫宫殿房檐设计恰好使北房在冬至前后阳光满屋,夏至前后屋檐遮阴.已知北京地区夏至前后正午太阳高度角约为75°,冬至前后正午太阳高度角约为30°,图1是顶部近似为正四棱锥、底部近似为正四棱柱的宫殿,图2是其示意图,则其出檐AB的长度(单位:米)约为( )
A.3 B.4 C. D.
5.已知数列满足,且,若,则正整数k为( )
A.13 B.12 C.11 D.10
6.如图,AB是圆O的一条直径,且.C,D是圆O上的任意两点,.点P在线段CD上,则的取值范围是( )
A. B. C. D.
7.已知直线,是函数图像相邻的两条对称轴,将的图像向右平移个单位长度后,得到函数的图像.若在上恰有三个不同的零点,则实数m的取值范围为( )
A. B. C. D.
8.已知,,,则( )
A. B. C. D.
二、多项选择题
9.设正实数a,b满足,则下列说法正确的是( )
A.的最小值为3 B.ab的最大值为1
C.的最小值为2 D.的最小值为2
10.函数的部分图象如图中实线所示,图中圆C与的图象交于M,N两点,且M在y轴上,则( )
A.函数在上单调递增
B.圆的半径为
C.函数的图象关于点成中心对称
D.函数在上单调递减
11.如图,在长方体中,E,F分别是棱,的中点,点P在侧面内,且,,则三棱锥外接球表面积的取值可能是( )
A. B. C. D.
12.已知数列满足,,则下列说法正确的有( )
A. B.
C.若,则 D.
三、填空题
13.已知,且,则______.
14.已知非零向量,满足,,若,则向量在向量方向上的投影向量的坐标为______.
15.已知数列满足,,若数列为单调递增数列,则的取值范围为______.
四、双空题
16.法国的拿破仑提出过一个几何定理:“以任意三角形的三条边为边向外构造三个等边三角形,则这三个等边三角形的外接圆圆心恰好是一个等边三角形的三个顶点.”在ABC中,,以AB,BC,AC为边向外作三个等边三角形,其外接圆圆心依次为,,,则______;若的面积为,则三角形中的最大值为______.
五、解答题
17.已知函数,将的图象向左平移个单位长度,所得函数的图象关于y轴对称.
(1)求函数的解析式;
(2)若关于x的方程在上恰有两个实数根,求实数a的取值范围.
18.已知函数.
(1)讨论函数的单调性;
(2)若,是否存在整数,都有恒成立,若存在求出实数m的最小值,若不存在说明理由.
19.设数列前n项和满足,.
(1)证明:数列为等比数列;
(2)记,求数列的前n项和.
20.如图,在四棱锥中,PAD为等边三角形,M为PA的中点,,平面平面ABCD.
(1)证明:平面平面PAB;
(2)若,,,直线PB与平面MCD所成角的正弦值为,求三棱锥的体积.
21.如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数,的图像,图像的最高点为.边界的中间部分为长1千米的直线段CD,且,游乐场的后一部分边界是以O为圆心的一段圆弧DE.
(1)求曲线段FGBC的函数表达式;
(2)曲线段FGBC上的入口G距海岸线EF最近距离为1千米,现准备从入口G修一条笔直的景观路到O,求景观路GO长;
(3)如图,在扇形ODE区域内建一个平行四边形休闲区OMPQ,平行四边形的一边在海岸线EF上,一边在半径OD上,另外一个顶点P在圆弧DE上,且,求平行四边形休闲区OMPQ面积的最大值及此时的值.
22.已知函数.
(1)求在的单调区间与最值;
(2)当时,若,证明:有且仅有两个零点.
参考答案
1.答案:B
解析:由已知中阴影部分所表示的集合元素满足“是B的元素,也是A的元素,不是C的元素”,故阴影部分所表示的集合是.故选:B.
2.答案:D
解析:先验证充分性:令,满足是纯虚数,
但是不满足,互为共轨复数,所以充分性不成立;
再验证必要性:令,满足,互为共轭复数,
但是不满足是纯虚数,所以必要性不成立,
所以“是纯虚数”是“,互为共轭复数”的既不充分也不必要条件.
故选:D.
3.答案:C
解析:
,定义域为R,
为奇函数,故图象关于原点对称,故排除A,D;
令,则,,故有无数个零点,故排除B.
故选:C.
4.答案:C
解析:如图:由题意可得
,,
中,由正弦定理可得
直角三角形中,
的长度为米,
故选:C.
5.答案:B
解析:由已知可得
,,,,
以上各式累加可得,
又,代入
,即
,解得,
故,
令,解得.
故选:B.
6.答案:D
解析:如图,O为圆心,连接,
则
因为点P在线段上且,则圆心到直线的距离,
所以,
所以,则,
即的取值范围是.
故选:D.
7.答案:A
解析:由题意可知的最小正周期为,所以,所以,则,故,令,解得,由图像可知解得.
故选A项.
8.答案:A
解析:下面先证明,(且).
记,则
,
令,得:;
令,得:;
函数在上单增,在上单减,所以对任意,都有,即恒成立,所以对任意且,都有,即恒成立,故,故,
构造函数,则
故当时,单调递增,
故,即,
综上.
故选:A.
9.答案:ABD
解析:
10.答案:CD
解析:根据函数的图象以及圆C的对称性,
可得M,N两点关于圆心对称,
所以,于是
,
由及,得
由于,所以,
所以,,从而,故半径为
,故B错误;
当时,,,因为在区间
上先减后培,所以原函数在上先减后增,故A错误;
,故C正确;
当时,,即
,此时为减函数,故D正确.
故选:CD.
11.答案:BCD
解析:如图,连接,,,易证四边形是平行四边形,
则点在线段上,取的中点G,连接,,
分别取,的中点,,连接,
易知三棱锥外接球的球心O在直线上,连接,,,,
设三棱锥外接球的半径为R,则,
因为,所以,,
所以,所以.
则当P与E重合时,
此时三棱锥外接球的半径取得最小值;
当P与重合时,
此时三棱锥外接球的半径取得最大值,
故三棱锥外接球表面积的取值范围是.
12.答案:BCD
解析:对于A:,,
,
,故A错误;
对于B:,
要证,
则证,
即证,
即证,
令,则,,
设,
,
当时,,函数单调递增,
当时,,函数单调递减,
,
恒成立,
,故B正确;
易知足遂增数列,所以,
则,
,
则,即
所以,
即,
所以,
所以
而当时,则有,
故C正确;
令函数,
则
所以在上单调递减,
所以当时,,
则,
所以
,
所以,D正确.
故选:BCD.
13.答案:
解析:因为,所以
故,
所以.
故答案为:.
14.答案:
解析:
15.答案:
解析:由题意可得时,,
当时,,即,对也成立,
则,,
,
若数列为单调道壇数列,则恒成立,
即
化为对恒成立.
设,则
当时,,
当时,为递减数列,即
可得为最大值,且为,
则.故答寀为:.
16.答案:,4
解析:
17.答案:(1);
(2)
解析:(1),
将函数的图象向左平移个单位长度后,
所得函数为,
,,,.
又,,.
(2),,
当,即时,单调递增;
当,即时,单调递减.
且,,.
方程在上恰有两个实数根,
,实数a的取值范围为.
18.答案:(1)单调性见解析;
(2)3
解析:(1),,
当,,在单调递增,
当时,,
令,得,得,
在单调递增,在单调递减.
综上,时,在单调递增;
当时,在单调递增,在单调递减.
(2),,
,,
令,,
令,,在单调递减.
,
,使得,即,,
当,,,单调递增,
当,,,单调递减,
,
,,,m的最小值为3.
19.答案:(1)证明见解析;
(2)
解析:(1)证明:,且,
,
,,
令,可得,,
所以数列是首项为,公比为的等比数列.
(2)由(1)可得,
,,
,
.
20.答案:(1)证明见解析;
(2)
解析:(1)取AD中点为N,连接PN,
因为PAD为等边三角形,所以,
且平面平面ABCD,平面平面,面PAD,
所以平面ABCD,
又平面ABCD,所以,
又因为,,平面PAD,
所以平面PAD,
又因为平面PAD,所以,
因为M为AP中点,所以,且,平面PAD,
所以平面PAB,且平面CDM,
所以平面平面PAB.
(2)由(1)可知,且,,
所以平面PAD,且平面PAD,所以,
以A为坐标原点,分别以AB,AD所在直线为x,y轴,建立如图所示空间直角坐标系,
设,则可得
,,,,,,
即,,,
设平面MCD的法向量为,
则
则可得,取,则,,
所以平面MCD的一个法向量为,
设直线PB与平面MCD所成角为,
所以,
解得,或,即(舍去)或1,
所以,.
21.答案:(1),;
(2)千米;
(3)时,平行四边形面积最大值为
解析:(1)由已知条件,得,
又,,.
又当时,有,,
曲线段FBC的解析式为,.
(2)由得,
又,,,,,
景观路GO长为千米.
(3)如图,,,,,
作轴于点,在中,,
在中,,
,
,
当时,即时,平行四边形面积最大值为.
22.答案:(1)的增区间为:,,减区间为:,;的最大值为,最小值为;
(2)证明见解析.
解析:(1),
解得或0或,
与的分布列如下:
x 0
+ - + -
↑ 极大值 ↓ 极小值1 ↑ 极大值 ↓
所以,的增区间为:,,减区间为:,,
的最大值为,最小值为.
(2)的定义域为R,
,
所以为偶函数.
,当时,有且仅有两个零点
当时,在上有且仅有一个零点.
,
当时,若,则,所以在上单调递减,
,在上有且仅有一个零点;
当时,存在,使得,
当时,,
当时,,
当时,,
所以,在递增,在上递减,
在上单调递增,
,,可得,
当时,,
所以,
所以,在上有且仅有一个零点,综上,当时,有且仅有两个零点.
同课章节目录
