四年级下册数学北师大版 《密铺》课件(共20张PPT)
文档属性
| 名称 | 四年级下册数学北师大版 《密铺》课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-28 06:57:57 | ||
图片预览








文档简介
(共20张PPT)
数学好玩
探索:密铺
观察下列图片,说一说什么是密铺。
密铺,即面图形的镶嵌,用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
什么图形可以密铺?
为什么有的图形可以密铺呢?
提出问题
······
这些问题,我们都留到课后来探索
相信认真听讲的你,马上就会解答出来!
本次活动任务:
三角形能不能密铺?
四边形可不可以?
设计方案
1.解决这个问题需要哪些步骤?
2.你想采取怎样的方式解决问题?(独立完成&小组合作)
如果是小组合作,怎样进行分工?
3.把主要步骤、分工写下来
动笔写一写吧!
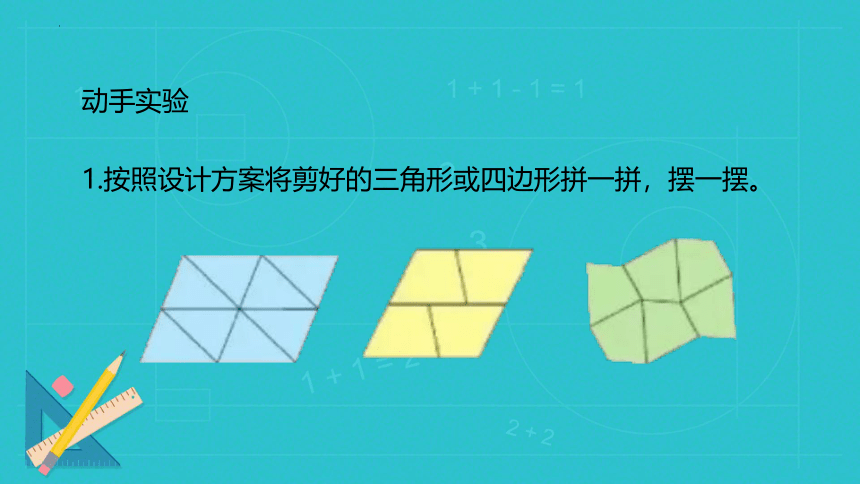
动手实验
1.按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
2.全班交流密铺的作品,三角形能不能密铺?四边形呢?
三角形和四边
形都可以密铺
为什么可以呢?
为什么三角形和四边形都可以密铺呢?
密铺的定义 用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
三角形的内角和是180°,是一个周角的一半,四边形的内角和是360°,正好是一个周角,所以三角形和四边形都可以密铺。
交流反思
1.请按照下面的方法试一试,你有什么发现?
2.在上面的活动中,你有什么收获?还有那些想要进一步研究的
问题?
密铺与图形的
角有关系······
所有的图形
都能密铺吗?
让我们继续写下去!
结合下面的图形说一说:真的什么图形都能密铺吗?
并不是所有图形都可以密铺的:
正三角形、正四边形和正六边形外,其它正多边形都不可以密铺。
正六边形可以密铺,因为它的每个内角都是120°,在每个拼接点处恰好能容纳3个内角;正五边形不可以密铺,因为它的每个内角都是108度,而360°不是108的整数倍,在每个拼接点处的内角不能保证没空隙或重叠现象;除正三角形、正四边形和正六边形外,其它正多边形都不可以密铺平面。
数学小tip
可以单独密铺的图形:
①任意三角形、任意凸四边形都可以密铺。
②正三角形、正四边形、正六边形可以单独用于平移密铺。
③三对对应边平行的六边形可以单独密铺。
④目前仅发现十五类五边形能密铺。
4.看一看下面的密铺图案,想一想它们是如何形成的
留心观察,你
会发现有很多
密铺现象。
好啦,现在我们来解答刚刚提出的问题
1.什么图形可以密铺?
2.为什么有的图形可以密铺呢?
来聊聊你的收获吧!
谢谢大家!
数学好玩
探索:密铺
观察下列图片,说一说什么是密铺。
密铺,即面图形的镶嵌,用形状、大小完全相同的几种或几十种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
什么图形可以密铺?
为什么有的图形可以密铺呢?
提出问题
······
这些问题,我们都留到课后来探索
相信认真听讲的你,马上就会解答出来!
本次活动任务:
三角形能不能密铺?
四边形可不可以?
设计方案
1.解决这个问题需要哪些步骤?
2.你想采取怎样的方式解决问题?(独立完成&小组合作)
如果是小组合作,怎样进行分工?
3.把主要步骤、分工写下来
动笔写一写吧!
动手实验
1.按照设计方案将剪好的三角形或四边形拼一拼,摆一摆。
2.全班交流密铺的作品,三角形能不能密铺?四边形呢?
三角形和四边
形都可以密铺
为什么可以呢?
为什么三角形和四边形都可以密铺呢?
密铺的定义 用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图形的密铺,又称做平面图形的镶嵌。
三角形的内角和是180°,是一个周角的一半,四边形的内角和是360°,正好是一个周角,所以三角形和四边形都可以密铺。
交流反思
1.请按照下面的方法试一试,你有什么发现?
2.在上面的活动中,你有什么收获?还有那些想要进一步研究的
问题?
密铺与图形的
角有关系······
所有的图形
都能密铺吗?
让我们继续写下去!
结合下面的图形说一说:真的什么图形都能密铺吗?
并不是所有图形都可以密铺的:
正三角形、正四边形和正六边形外,其它正多边形都不可以密铺。
正六边形可以密铺,因为它的每个内角都是120°,在每个拼接点处恰好能容纳3个内角;正五边形不可以密铺,因为它的每个内角都是108度,而360°不是108的整数倍,在每个拼接点处的内角不能保证没空隙或重叠现象;除正三角形、正四边形和正六边形外,其它正多边形都不可以密铺平面。
数学小tip
可以单独密铺的图形:
①任意三角形、任意凸四边形都可以密铺。
②正三角形、正四边形、正六边形可以单独用于平移密铺。
③三对对应边平行的六边形可以单独密铺。
④目前仅发现十五类五边形能密铺。
4.看一看下面的密铺图案,想一想它们是如何形成的
留心观察,你
会发现有很多
密铺现象。
好啦,现在我们来解答刚刚提出的问题
1.什么图形可以密铺?
2.为什么有的图形可以密铺呢?
来聊聊你的收获吧!
谢谢大家!
