数学：2.4证明（湘教版九年级上）

本资料来自于资源最齐全的２１世纪教育网www.21cnjy.com
课时评价13 证明（1）
考标要求
1了解证明的含义，理解证明的必要性；
2 了解证明的基本步骤和书写格式。
重点难点：
重点：用平行线的性质、判定定理、三角形的性质定理证明有关几何问题
难点：正确填写理由以及寻找证明思路
一 填空题（每小题5分，共25分）
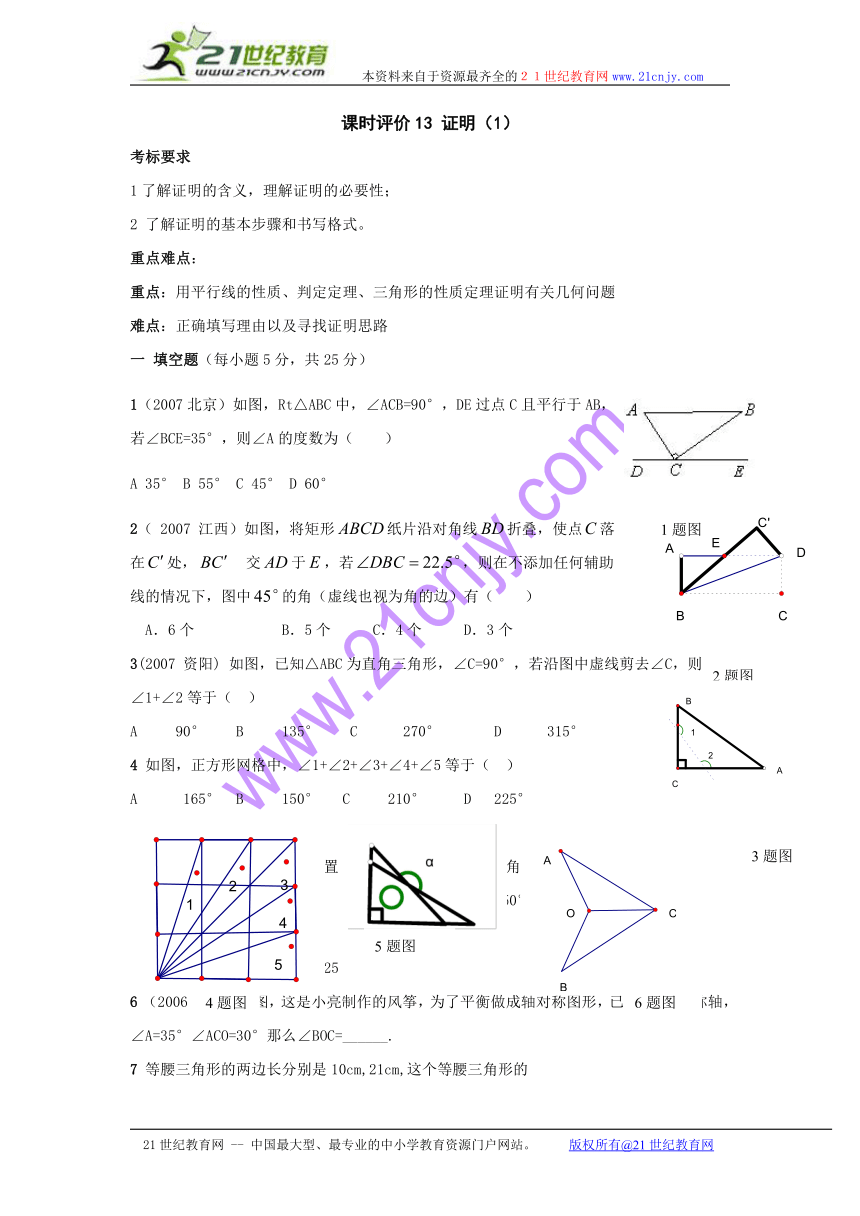
1（2007北京）如图，Rt△ABC中，∠ACB=90°，DE过点C且平行于AB，若∠BCE=35°，则∠A的度数为（ ）
A 35° B 55° C 45° D 60°
2（ 2007 江西）如图，将矩形纸片沿对角线折叠，使点落
在处， 交于，若，则在不添加任何辅助
线的情况下，图中的角（虚线也视为角的边）有（ ）
A．6个 B．5个 C．4个 D．3个
3(2007 资阳) 如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则
∠1+∠2等于（ ）
A 90° B 135° C 270° D 315°
4 如图，正方形网格中，∠1+∠2+∠3+∠4+∠5等于（ ）
A 165° B 150° C 210° D 225°
5把一副三角板按如图方式放置，则两条斜边所形成的钝角α=( )
A 75° B 105° C 135° D 150°
二 填空题（每小题5分，共25分）
6 （2006 扬州）如图，这是小亮制作的风筝，为了平衡做成轴对称图形，已知OC是对称轴，∠A=35°∠ACO=30°那么∠BOC=______.
7 等腰三角形的两边长分别是10cm,21cm,这个等腰三角形的
周长等于_______cm.
8 已知三角形三边长a、b、c满足(a+b+c)(a+b-c)=2ab,则此三角形是________三角形。
9 （2007 贵阳）在△ABC中，若AB=8，BC=6，则第三边AC的长度m的取值范围是________
10 如图，两平面镜α、β的夹角θ，入射光线AO平行于β，入射到α上，经两次反射的
出射光线BO’ 平行于α,则角，θ=______
三 解答题（12×3+14=50分）
11 如图在△ABC中，∠B的平分线交∠C的外角平分线∠ACE的平分线于点D，那么∠A
与∠D有怎样的数量关系,证明你的结论。
12 某学校初中三年级学生在参加综合实践活动中，看到工人师傅在材料的边角处画直角时，有时用“三弧法”，如图所示，方法是：（1） 画线段AB，分别以A、B为圆心，AB为半径画弧，两弧交于C点；(2) 在AC延长线上截取CD=CB；（3）连接DB，则得到直角
∠ABC，你知道这是为什么吗？请说明理由。
13 证明：如图，EG∥AF,请你从下面三个条件中，再选两个作为已知
条件，另一个作为结论，推出一个正确的命题（只写出一种情况）
（1） AB=AC （2） DE=DF (3) BE=CF
已知：EG∥AF,____=_______,______=_______.
求证：___=____
14 （2007福州）如图，直线AC∥BD，连接AB,直线AC、BD及线段AB把平面分成①、②、③、④四个部分，规定：线上各点不属于任何部分，当动点P落在某个部分时，连接PA、PB,构成∠PAC、∠APB、∠PBD三个角。（提示：有共同端点的两条重合的射线所组成的角是0°）
(1) 当动点P落在第一部分时，求证：∠APB=∠PAC+∠PBD
（2）当动点P落在第二部分时，∠APB=∠PAC+∠PBD是否还成立（直接回答成立或不成立）？
（3）当动点P 在第三部分时，全面探究∠PAC、∠APB、∠PBD之间的关系，并写出动点P的具体位置和相应的结论，选择其中一种结论加以证明
课时评价13 2.4 证明（1）
1 B 2 B 3 C 4 D 5 A 6 115° 7 52 8 直角 9 211 ∵∠D=∠DCE-∠DBE ,∠A=2∠DCE-2∠DBE=2(∠DCE-∠DBE)∴∠D=2∠A
12∵AC=BC ∴∠A=∠CBA ∵CB=CD ∴∠D=∠CBD ∵∠A+∠D+∠CBA+∠CBD=180°∴2(∠CBA+∠CBD)=180°∴∠∠CBA+∠CBD=90°即：∠ABD=90°∴△ABD是直角三角形
13 （答案不唯一）如选AB=AC,DE=DF作已知，BE=CF作结论，证明如下：
易证：△DEG≌△DFC,∴CF=EG ∵EG∥AC ∴ ∠EGB=∠ACB ∵AB=AC
∴ ∠B=∠ACB ∴ ∠B=∠EGB∴ BE=EG ∴ BE=CF
14 (1)如图1作PE∥AC交AB于E, ∵AC∥BD ,∴PE∥BD,
∴ ∠APE=∠PAC ,∠BPE=∠PBD, ∴∠APB=∠PAC+∠PBD
即：∠APB=∠PAC+∠PBD
(2)不成立
（3）(a)当动点P在射线BA的右侧时，结论是
∠PBD=∠PAC+∠APB .
(b)当动点P在射线BA上，
结论是∠PBD =∠PAC +∠APB .
或∠PAC =∠PBD +∠APB 或 ∠APB = 0°，
∠PAC =∠PBD（任写一个即可）.
(c) 当动点P在射线BA的左侧时，
结论是∠PAC =∠APB +∠PBD .
选择(a) 证明：
如图9-4，连接PA，连接PB交AC于M
∵ AC∥BD ,
∴ ∠PMC =∠PBD .
又∵∠PMC =∠PAM +∠APM ,
∴ ∠PBD =∠PAC +∠APB .
选择(b) 证明：如图9-5
∵ 点P在射线BA上，∴∠APB = 0°.
∵ AC∥BD , ∴∠PBD =∠PAC .
∴ ∠PBD =∠PAC +∠APB
或∠PAC =∠PBD+∠APB
或∠APB = 0°，∠PAC =∠PBD.
选择(c) 证明：
如图9-6，连接PA，连接PB交AC于F
∵ AC∥BD , ∴∠PFA =∠PBD .
课时评价14 证明（2）
1 D 2 D 3 B 4 D 5 B 6 4 7 3 8 70° 40° 40°或70°70°40°
9 等腰三角形10 45 11 ∵OP平分∠AOC和∠BOD，∴ ∠BOP=∠DOP, ∠AOP=COP,∴∠AOB=∠COD,又∵OA=OC,OB=OD,∴△OAB≌△OCD，∴AB=CD
12 ∵AF平分∠BAC,∴∠BAD=∠CAD,∵DE∥AC, ∴∠EDA=∠CAD=∠BAD,∴AE=ED∵∠EDB+∠ADE=90°∴∠BDE+∠BAD=90°∵∠EBD+∠BAD=90°∴∠BDE=∠EBD
∴BE=ED∴AE=BE
13 3cm
14 如图
15 (1)易证△ABD≌△CAE
∴AD=CE
（2）由（1）知，∠BAD=∠ACE
∴∠DFC=∠DAC+∠ACE
=∠DAC+∠BAD=60°
图2
图1
图1
14题图
13题图
12题图
11题图
10题图
6题图
4题图
5题图
3题图
2题图
1题图
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网