4.1.2 折射定律的应用 课件(共38张PPT)2023-2024学年高二上学期物理人教版(2019)选择性必修第一册
文档属性
| 名称 | 4.1.2 折射定律的应用 课件(共38张PPT)2023-2024学年高二上学期物理人教版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 74.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-06-28 20:16:20 | ||
图片预览



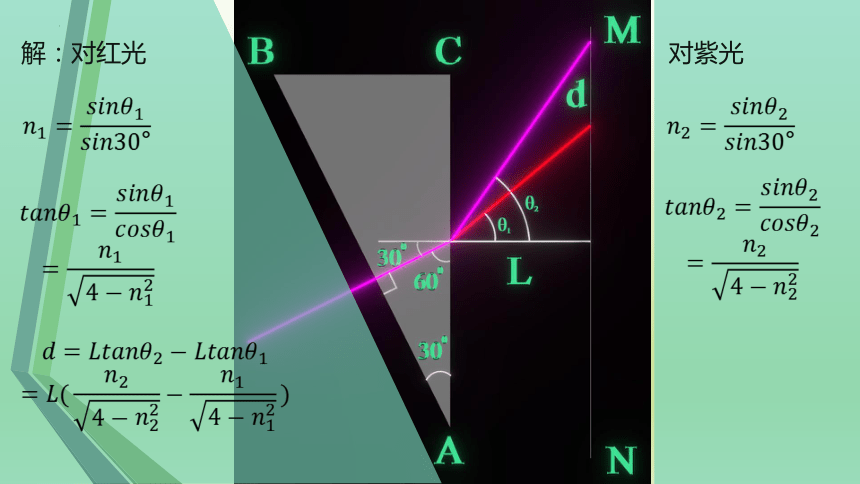

文档简介
(共38张PPT)
折射定律的应用
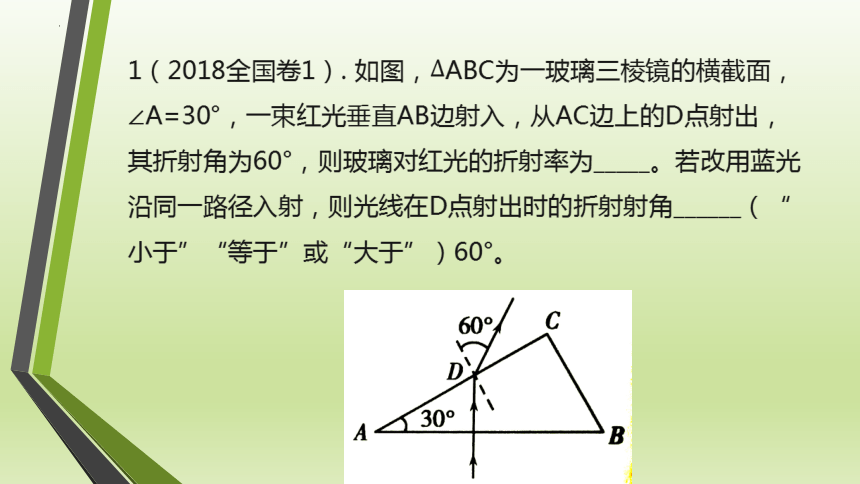
1(2018全国卷1). 如图,ABC为一玻璃三棱镜的横截面,∠A=30°,一束红光垂直AB边射入,从AC边上的D点射出,其折射角为60°,则玻璃对红光的折射率为_____。若改用蓝光沿同一路径入射,则光线在D点射出时的折射射角______(“小于”“等于”或“大于”)60°。
几何光学题目的特点
1 知识点单一,解法单一:折射定律
2 注意事项:分界面、法线、入射角、折射角、折射率
3难点:光路图
解:
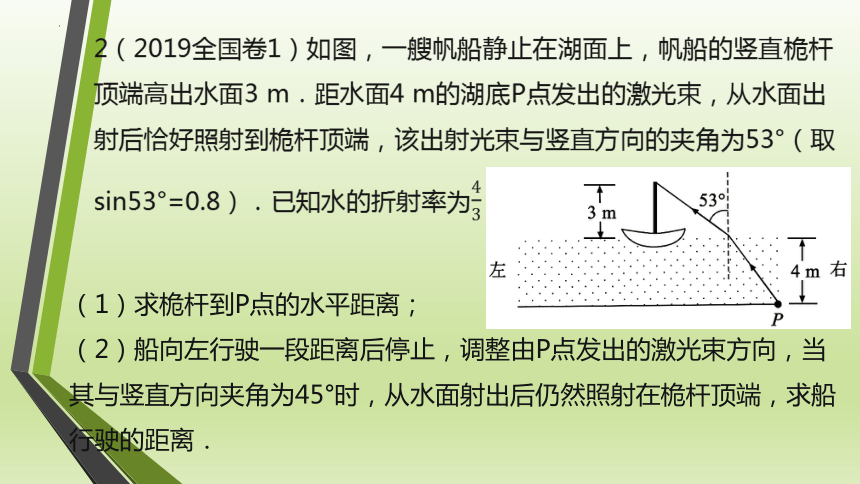
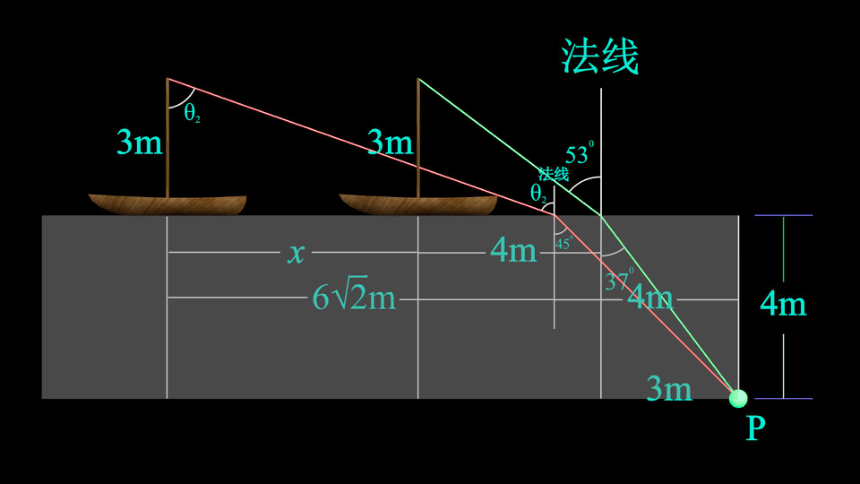
2(2019全国卷1)如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m.距水面4 m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin53°=0.8).已知水的折射率为
(1)求桅杆到P点的水平距离;
(2)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍然照射在桅杆顶端,求船行驶的距离.
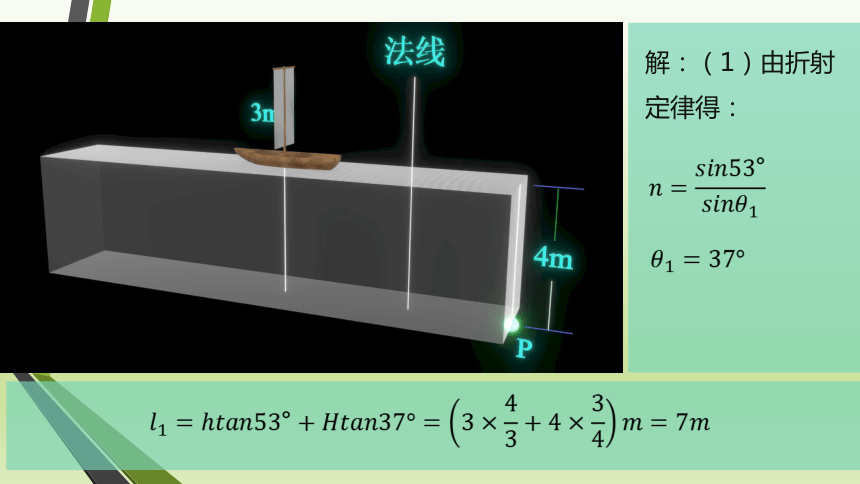
解:(1)由折射定律得:
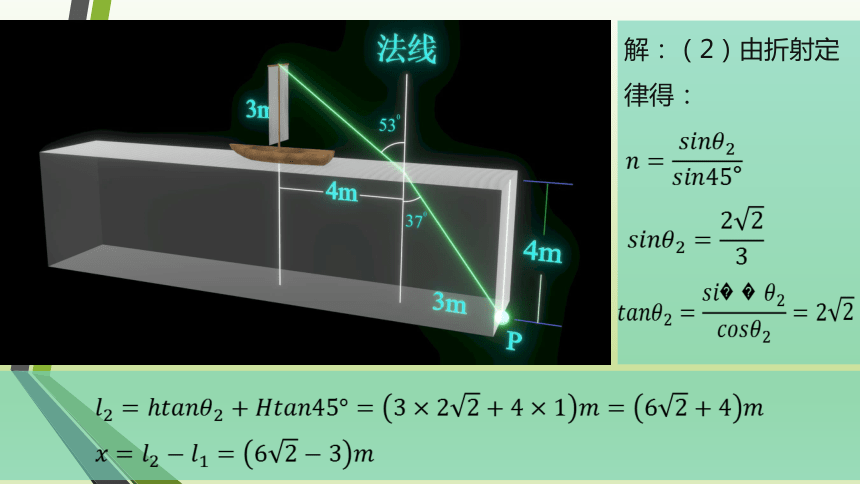
解:(2)由折射定律得:
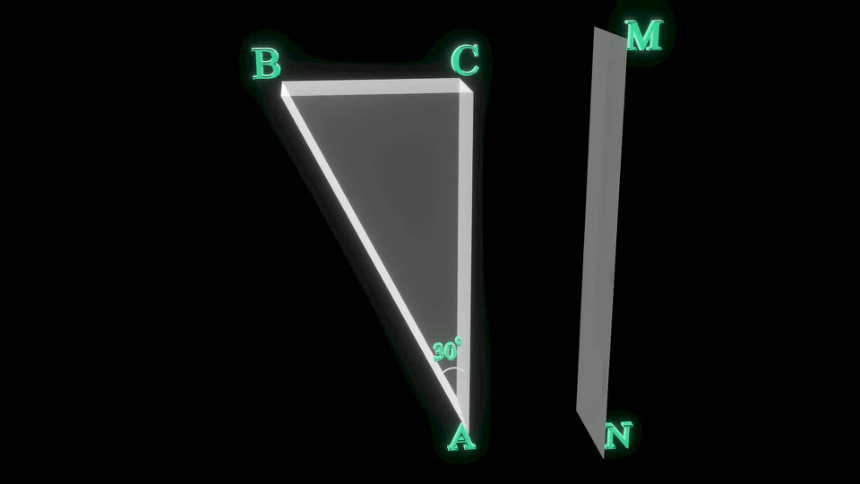
3(2013海南卷)如图所示,三棱镜的横截面为直角三角形ABC,∠A=30°,AC平行于光屏MN,与光屏的距离为L,棱镜对红光的折射率为n1,对紫光的折射率为n2。一束很细的白光由棱镜的侧面AB垂直射入,直接到达AC面并射出。画出光路示意图,并标出红光和紫光射在光屏上的位置,求红光和紫光在光屏上的位置之间的距离。
A
B
C
M
N
解:对红光
对紫光
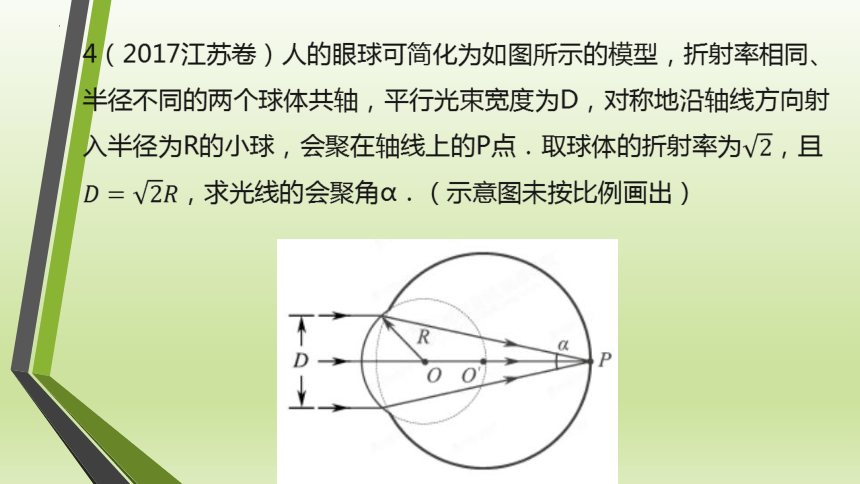
4(2017江苏卷)人的眼球可简化为如图所示的模型,折射率相同、半径不同的两个球体共轴,平行光束宽度为D,对称地沿轴线方向射入半径为R的小球,会聚在轴线上的P点.取球体的折射率为,且,求光线的会聚角α.(示意图未按比例画出)
解:
5(2018全国卷3)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点做AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察。恰好可以看到小标记的像;过O点做AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
如果无法证明猜想怎么办?
1 先假设猜想成立,计算相关角度长度,检查有无问题,如果没有问题,就可以认为猜想正确(有风险,需谨慎)
2 时间允许,证明猜想成立
解:由几何关系得:
解:由几何关系得:
6(2017全国卷1)如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高位2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R。已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
解的存在性和唯一性
解:由几何关系得:
入射角是
由正弦定理得:
唯一性的证明:
代入上式得:
(
(
解得:
解得:(舍)
7(2017全国卷2)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
解:
对光线1:
对光线2:
解得:
8(2016全国卷3)如图所示,玻璃球冠的折射率为,其底面镀银,底面半径是球半径的倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点。求该光线从球面射出的方向相对于其初始入射方向的偏角。
解:
由几何关系可知:为等边三角形,入射角等于
由折射定律得:
解得:
由几何关系可知:在底面上入射角为
解得:
这说明底面的反射光线经过球心
光线的偏角为
9(2008全国卷2).一束单色光斜射到厚平板玻璃的一个表面上,经两次折射后从玻璃板另一个表面射出,出射光线相对于入射光线侧移了一段距离。在下列情况下,出射光线侧移距离最大的是( )
A.红光以的入射角入射
B.红光以的入射角入射
C.紫光以的入射角入射
D.紫光以的入射角入射
9(2008全国卷2).一束单色光斜射到厚平板玻璃的一个表面上,经两次折射后从玻璃板另一个表面射出,出射光线相对于入射光线侧移了一段距离。在下列情况下,出射光线侧移距离最大的是( )
A.红光以的入射角入射
B.红光以的入射角入射
C.紫光以的入射角入射
D.紫光以的入射角入射
入射角一定,折射率增大, 减小,增大,排除AB。
讨论(1)
解:
(2)折射率一定,入射角增大, 增大,
两边同时对求导
入射角增大,增大,
排除C,最终答案为D
谢谢观看
折射定律的应用
1(2018全国卷1). 如图,ABC为一玻璃三棱镜的横截面,∠A=30°,一束红光垂直AB边射入,从AC边上的D点射出,其折射角为60°,则玻璃对红光的折射率为_____。若改用蓝光沿同一路径入射,则光线在D点射出时的折射射角______(“小于”“等于”或“大于”)60°。
几何光学题目的特点
1 知识点单一,解法单一:折射定律
2 注意事项:分界面、法线、入射角、折射角、折射率
3难点:光路图
解:
2(2019全国卷1)如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m.距水面4 m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin53°=0.8).已知水的折射率为
(1)求桅杆到P点的水平距离;
(2)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍然照射在桅杆顶端,求船行驶的距离.
解:(1)由折射定律得:
解:(2)由折射定律得:
3(2013海南卷)如图所示,三棱镜的横截面为直角三角形ABC,∠A=30°,AC平行于光屏MN,与光屏的距离为L,棱镜对红光的折射率为n1,对紫光的折射率为n2。一束很细的白光由棱镜的侧面AB垂直射入,直接到达AC面并射出。画出光路示意图,并标出红光和紫光射在光屏上的位置,求红光和紫光在光屏上的位置之间的距离。
A
B
C
M
N
解:对红光
对紫光
4(2017江苏卷)人的眼球可简化为如图所示的模型,折射率相同、半径不同的两个球体共轴,平行光束宽度为D,对称地沿轴线方向射入半径为R的小球,会聚在轴线上的P点.取球体的折射率为,且,求光线的会聚角α.(示意图未按比例画出)
解:
5(2018全国卷3)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点做AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察。恰好可以看到小标记的像;过O点做AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
如果无法证明猜想怎么办?
1 先假设猜想成立,计算相关角度长度,检查有无问题,如果没有问题,就可以认为猜想正确(有风险,需谨慎)
2 时间允许,证明猜想成立
解:由几何关系得:
解:由几何关系得:
6(2017全国卷1)如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高位2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R。已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
解的存在性和唯一性
解:由几何关系得:
入射角是
由正弦定理得:
唯一性的证明:
代入上式得:
(
(
解得:
解得:(舍)
7(2017全国卷2)一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
解:
对光线1:
对光线2:
解得:
8(2016全国卷3)如图所示,玻璃球冠的折射率为,其底面镀银,底面半径是球半径的倍;在过球心O且垂直于底面的平面(纸面)内,有一与底面垂直的光线射到玻璃球冠上的M点,该光线的延长线恰好过底面边缘上的A点。求该光线从球面射出的方向相对于其初始入射方向的偏角。
解:
由几何关系可知:为等边三角形,入射角等于
由折射定律得:
解得:
由几何关系可知:在底面上入射角为
解得:
这说明底面的反射光线经过球心
光线的偏角为
9(2008全国卷2).一束单色光斜射到厚平板玻璃的一个表面上,经两次折射后从玻璃板另一个表面射出,出射光线相对于入射光线侧移了一段距离。在下列情况下,出射光线侧移距离最大的是( )
A.红光以的入射角入射
B.红光以的入射角入射
C.紫光以的入射角入射
D.紫光以的入射角入射
9(2008全国卷2).一束单色光斜射到厚平板玻璃的一个表面上,经两次折射后从玻璃板另一个表面射出,出射光线相对于入射光线侧移了一段距离。在下列情况下,出射光线侧移距离最大的是( )
A.红光以的入射角入射
B.红光以的入射角入射
C.紫光以的入射角入射
D.紫光以的入射角入射
入射角一定,折射率增大, 减小,增大,排除AB。
讨论(1)
解:
(2)折射率一定,入射角增大, 增大,
两边同时对求导
入射角增大,增大,
排除C,最终答案为D
谢谢观看
