小升初分班考易错题检测卷(试题)2023-2024学年数学六年级下册人教版(含答案)
文档属性
| 名称 | 小升初分班考易错题检测卷(试题)2023-2024学年数学六年级下册人教版(含答案) | 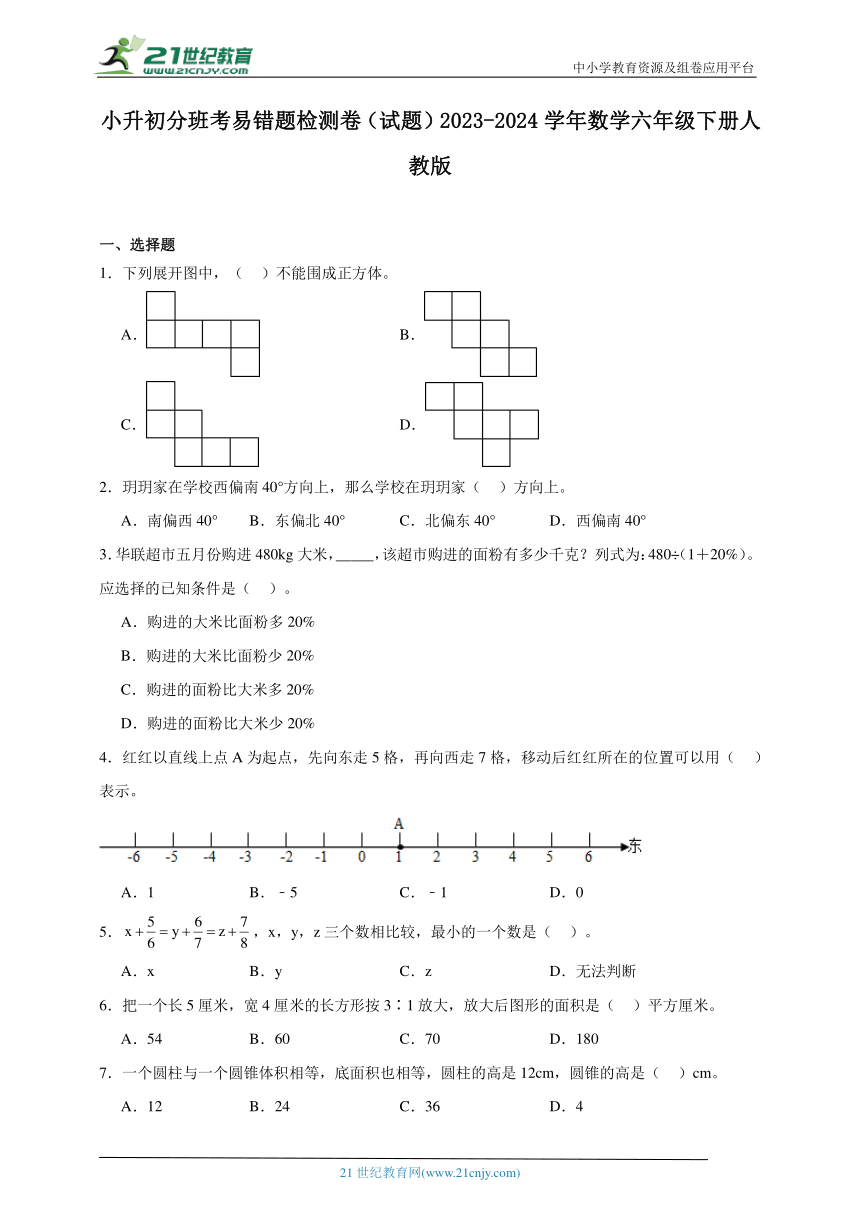 | |
| 格式 | docx | ||
| 文件大小 | 468.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 10:12:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考易错题检测卷(试题)2023-2024学年数学六年级下册人教版
一、选择题
1.下列展开图中,( )不能围成正方体。
A. B.
C. D.
2.玥玥家在学校西偏南40°方向上,那么学校在玥玥家( )方向上。
A.南偏西40° B.东偏北40° C.北偏东40° D.西偏南40°
3.华联超市五月份购进480kg大米,_____,该超市购进的面粉有多少千克?列式为:480÷(1+20%)。应选择的已知条件是( )。
A.购进的大米比面粉多20%
B.购进的大米比面粉少20%
C.购进的面粉比大米多20%
D.购进的面粉比大米少20%
4.红红以直线上点A为起点,先向东走5格,再向西走7格,移动后红红所在的位置可以用( )表示。
A.1 B.﹣5 C.﹣1 D.0
5.,x,y,z三个数相比较,最小的一个数是( )。
A.x B.y C.z D.无法判断
6.把一个长5厘米,宽4厘米的长方形按3∶1放大,放大后图形的面积是( )平方厘米。
A.54 B.60 C.70 D.180
7.一个圆柱与一个圆锥体积相等,底面积也相等,圆柱的高是12cm,圆锥的高是( )cm。
A.12 B.24 C.36 D.4
8.某品牌饮料搞促销活动,甲商场满100元减20元;乙商场一律打八折;丙商场买十送二。该饮料在三个商场的单价都是8元,李阿姨要买36瓶该品牌饮料,( )更省钱。
A.甲商场 B.乙商场 C.丙商场 D.无法确定谁
二、填空题
9.一匹布可以做8件上衣或10条裤子。现已做了1条裤子,剩下的要成套做可以做( )套。
10.有一个质数,它既是两个质数的和,又是两个质数的差,这个质数是( )。
11.A、B、C、D、E五人进行乒乓球比赛,每两个人都要赛一场。现在A、D赛了4场,B、C各自赛了3场,E至少赛( )场。
12.学生甲在一列队伍的排尾以每小时6千米的速度赶到队伍排头后,又以同样的速度返回队尾,一共用了3小时,若队伍进行的速度为每小时4千米,则队伍长为( )千米。
13.一瓶酒精,第一次倒出,然后倒回瓶中40克;第二次倒出瓶中剩下部分的。第三次倒出270克,瓶中还剩80克。原来瓶中有( )克。
14.对于任意自然数a、b,如果a*b=2a+6b,已知,那么x=( )。
15.一项工程,甲单独做需要10天,乙单独做需要15天,丙的工效比甲低但比乙高,三人合作最少需要( )天。(结果取整数)
16.甲、乙两个圆柱形容器,底面积比为6∶4,甲容器中水深18厘米,乙容器中水深12厘米,再往两个容器中注入同样多的水,使得两个容器中水一样深,这时水深( )厘米。
三、判断题
17.一筐苹果比一筐梨重20%,那么一筐梨就比一筐苹果轻20%。( )
18.X和Y表示两种变化的相关联的量,同时5X—7Y=0,X和Y不成比例.( )
19.小芳今年a岁,妈妈今年b岁,5年后妈妈比小芳大(b-a+5)岁。( )
20.把一根米长的绳子分成5段,每段占全长的。( )
21.医生需要监测病人的体温情况,应选用折线统计图。( )
四、计算题
22.直接写出结果。
×24= 15÷= 4.2×= ÷=
1÷= ÷= -= ÷×=
23.脱式计算。
(1)13.7×9.9+13.7×0.1 (2)+(1-)
24.解方程(或比例)。
(1)x-x= (2)x∶=8∶
五、解答题
25.一种食品油,由于成本提高,现在每升比原来的价格增加了二成,原来每升油15元,现在每升油多少元?
26.一辆运货汽车从甲地到乙地,平均每小时行72千米,10小时到达。回来时空车原路返回,每小时可行90千米。多长时间能够返回原地?
27.修一条长480米的路,如果单独修完,甲乙两队所用的时间比是5∶7,现在让两队同时修这条路,完成时,甲队比乙队多修多少米?
28.一个圆锥形的煤堆,占地50m2,高2.4m.如果每立方米煤重1.5t,用一辆载质量为6t的卡车来运,至少几次能全部运完?
29.如图,在长方形ABCD中,厘米,厘米,平行四边形BCEF的一边BF交CD于点G,若梯形CEFG的面积为64平方厘米,则DG的长为多少?
30.滨海村各种作物种植面积的分布情况如图所示,请根据统计图回答以下问题:
(1)花生的种植面积与向日葵种植面积的最简单的整数比是( )。
(2)如果花生的种植面积是6.6公顷,那么大豆与芝麻的种植面积一共是多少公顷?(列式解答)
参考答案:
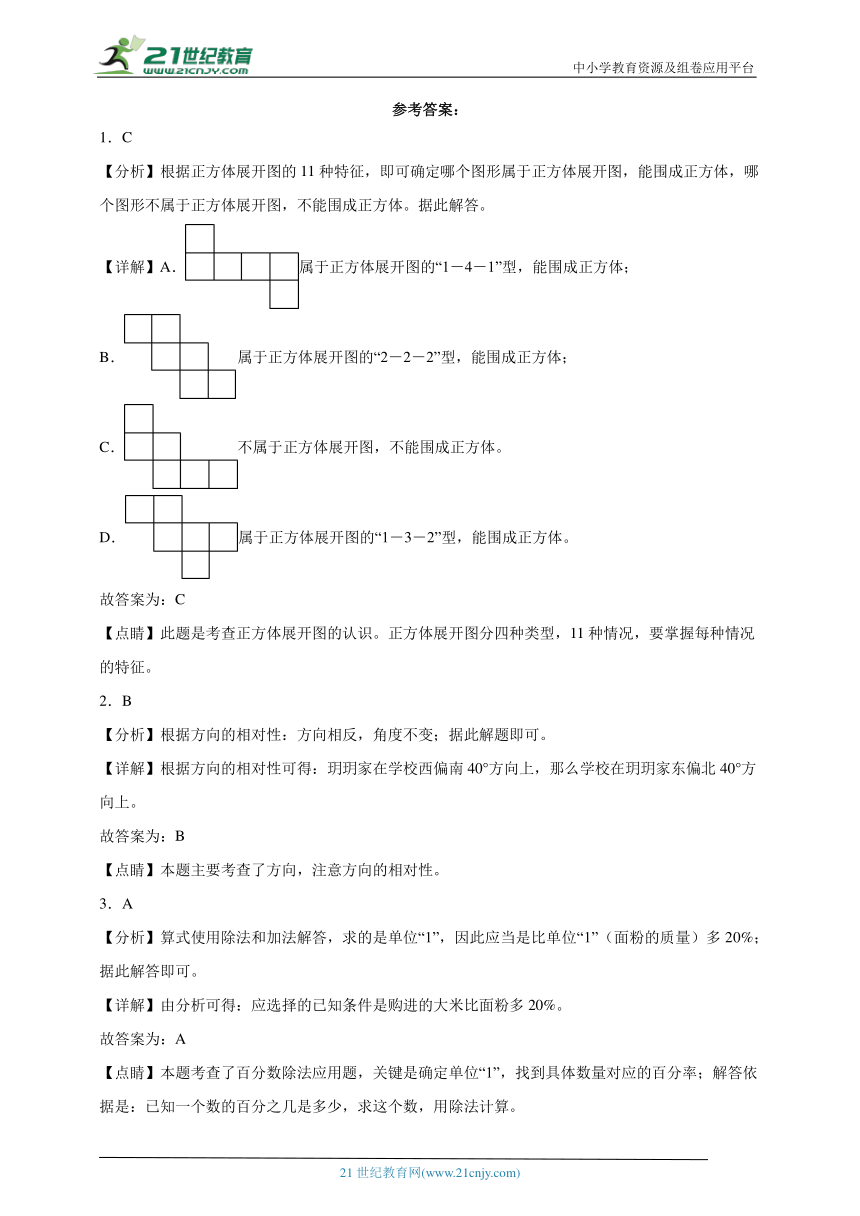
1.C
【分析】根据正方体展开图的11种特征,即可确定哪个图形属于正方体展开图,能围成正方体,哪个图形不属于正方体展开图,不能围成正方体。据此解答。
【详解】A.属于正方体展开图的“1-4-1”型,能围成正方体;
B.属于正方体展开图的“2-2-2”型,能围成正方体;
C.不属于正方体展开图,不能围成正方体。
D.属于正方体展开图的“1-3-2”型,能围成正方体。
故答案为:C
【点睛】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
2.B
【分析】根据方向的相对性:方向相反,角度不变;据此解题即可。
【详解】根据方向的相对性可得:玥玥家在学校西偏南40°方向上,那么学校在玥玥家东偏北40°方向上。
故答案为:B
【点睛】本题主要考查了方向,注意方向的相对性。
3.A
【分析】算式使用除法和加法解答,求的是单位“1”,因此应当是比单位“1”(面粉的质量)多20%;据此解答即可。
【详解】由分析可得:应选择的已知条件是购进的大米比面粉多20%。
故答案为:A
【点睛】本题考查了百分数除法应用题,关键是确定单位“1”,找到具体数量对应的百分率;解答依据是:已知一个数的百分之几是多少,求这个数,用除法计算。
4.C
【分析】在一对具有相反意义的量中,向东为正,向西为负,根据题干,结合数轴起点A的位置进行解答即可。
【详解】由分析可得:移动后红红所在的位置可以用﹣1表示。
故答案为:C
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
5.C
【分析】三个算式的和相等,利用异分母异分子分数比较大小的方法,比较出三个算式中的数字加数的大小,就可以比较出三个字母的大小。
【详解】,,
可得;
且,所以x>y>z。
故答案为:C
【点睛】两个加法算式的和相等,如果甲算式中的一个加数大于乙算式的一个加数,则甲算式中的另一个加数一定小于乙算式的另一个加数。
6.D
【分析】根据题意,把长、宽按3∶1放大,先分别求出放大后的长、宽各是多少厘米,再根据长方形的面积公式:S=ab,把数据代入公式求出放大后的面积,即可进行解答。
【详解】放大后的长:5×3=15(厘米)
放大后的宽:4×3=12(厘米)
放大后图形的面积:15×12=180(平方厘米)
所以,放大后的面积是180平方厘米。
故答案为:D
【点睛】解答此题首先求出放大后的长、宽,再根据长方形的面积公式解答即可。
7.C
【分析】根据圆柱的体积公式,圆锥的体积公式,当圆柱和圆锥的体积、底面积分别相等时,圆锥的高是圆柱的高的3倍,由此求出圆锥的高,进而做出选择。
【详解】(cm)
故答案为:C
【点睛】此题主要考查了利用圆柱与圆锥的体积公式,推导出在体积、底面积分别相等时,圆柱的高与圆锥的高的关系。
8.B
【分析】甲商场:100元减20元现金,用总价减去减的现金即可求出要花的钱;乙商场:乙商场打八折,是指现价是原价的80%,根据单价×数量=总价,即可求出一共用多少元;丙商场:先求出买36个可以送几个,再根据实际买的个数乘单价求出花的钱数;比较即可求出哪家商场更省钱。
【详解】36×8-20
=288-20
=268(元)
8×80%×36
=6.4×36
=230.4(元)
36÷(10+2)
=36÷12
=3(组)
3×2=6(个)
(36-6)×8
=30×8
=240(元)
230.4<240<268
故答案为:B
【点睛】本题关键是根据各个商场不同的优惠方法求出每个商场要花的钱,通过比较得出哪个商场便宜。
9.4
【分析】把总布料看作单位“1”,用分数表示做一件上衣和一条裤子用的布料各占总布料的分率,剩下的布料可以做的套数=剩下布料占总布料的分率÷做一套衣服用去的布料占总布料的分率,据此解答。
【详解】假设总布料为1。
(1-)÷(+)
=÷
=4(套)
所以,剩下的要成套做可以做4套。
【点睛】本题主要考查分数除法的应用,求出做一套衣服需要的布料占总布料的分率是解答题目的关键。
10.5
【分析】所有的质数中2是唯一的偶质数,除2以外所有的质数都是奇数,那么这个质数一定是奇数,奇数与奇数的和(差)一定是偶数,奇数与偶数的和(差)一定是奇数,则这个质数的和或差中一定有一个质数是2,据此解答。
【详解】分析可知,和或差中有一个质数为2,2+3=5,7-2=5,2、3、5、7都是质数,符合题意,所以这个质数是5。
【点睛】掌握奇数和偶数的运算性质是解答题目的关键。
11.2
【分析】五人进行乒乓球比赛,每两个人都要赛一场,即每人都要和另外四个人赛一场,共赛4场。现在A、D都赛了4场,即A和D和除了自己以外的其它四人都赛了一场,B、C都赛了3场,则B这三场可和A、C、D各赛一场,C可和A、B、D各赛一场,所以E至少赛了2场,即和A、D各赛一场。
【详解】根据分析得,E至少赛2场。
【点睛】根据每人需要比赛的总场数及A、B、C、D已赛的场数进行推理分析,从而得出结论是完成本题的关键。
12.5
【分析】设这列队伍的长为x千米,此过程分两段,第一段是从队尾到排头的追及问题,此段所用的时间是小时,第二段是从排头到队尾的相遇问题,此段所用的时间是小时,一共用了3小时。根据等量关系:从队尾到排头的时间+从排头到队尾的时间=行走的时间,再列方程解答。
【详解】解:设这列队伍的长为x千米。
+=3
+=3
+=3
=3
x=3÷
x=5
即队伍长5千米。
【点睛】本题解题关键是理解“从队尾到排头的追及问题,从排头到队尾的相遇问题”,根据题目中的等量关系,再列方程解答。
13.885
【分析】第二次到出剩下酒精的,这时还剩下的(270+80)克,就是剩下酒精的(1-),求出第二次倒出前剩下的再减去40,就是全部酒精的(1-),据此解答。
【详解】(270+80)÷(1-)
=350÷
=630(克)
(630-40)÷(1-)
=590÷
=885(克)
【点睛】本题的关键是先求出第二次倒出前剩下酒精的重量。
14.896
【分析】定义新运算的一般解题步骤:
(1)关键问题:审题。正确理解定义的运算符号的意义。
(2)严格按照新定义的计算顺序,将数值代入算式中,准确找出要计算的习题中数据与定义中字母的对应关系,把它转化为一般的四则运算。
据此将转化成方程,求解即可。
【详解】
解:
【点睛】新的运算有自己的特点,适用于加法和乘法的运算定律不一定适用于定义运算,要特别注意运算顺序。
15.4
【分析】甲的工作效率是,乙的工作效率是,要想使三人合作天数最少,丙的工作效率就要尽可能的高,则丙的工作效率是,将工作总量看作单位“1”,1÷工作效率和=工作天数,据此分析。
【详解】1÷(++)
=1÷
≈4(天)
【点睛】关键是理解工作效率、工作时间、工作总量之间的关系,时间分之一可以看作效率。
16.30
【分析】根据体积相等时,圆柱的底面积和高成反比,底面积比为6:4,那么注入同体积的水的深度比是4:6,可设这时水深为x厘米,根据水的深度比,列出方程即可解答。
【详解】解:设这时水深为x厘米。
【点睛】本题主要考查圆柱的体积公式的灵活运用,列出方程解决问题是比较直观的方法。
17.×
【分析】假设一筐梨的重量是“1”,则苹果的重量是梨质量的(1+20%)=120%,求一筐梨比一筐苹果轻百分之几,用20%除以120%计算即可。
【详解】20%÷(1+20%)×100%
=0.2÷1.2×100%
≈16.7%
一筐梨比一筐苹果轻16.7%,原题说法错误。
故答案为:×
【点睛】此题重点考查学生对单位“1”的确定,找准不同的单位“1”是解决此题的关键。
18.×
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【详解】因为5x﹣7y=0,
所以5x=7y,x:y=1.4(一定),
可以看出,x和y是两种相关联的量,x随y的变化而变化,
1.4是一定的,也就是x与y相对应数的比值一定,符合正比例的意义.
所以x与y成正比例关系.
19.×
【分析】因为年龄差始终不变,所以今年的年龄差就是5年后的年龄差,用减法求出两人今年的年龄差即可。
【详解】两人的年龄差不变,都是:(b a)岁
故答案为:×
【点睛】解题关键是明确年龄差是一个不变量,求出今年的年龄差即可。
20.×
【分析】把一根米长的绳子看作一个整体,把它平均分成5份,其中的1份用分数表示是。
【详解】把一根米长的绳子平均分成5段,每段占全长的,原题缺少“平均”两字。
故答案为:×
【点睛】本题重点考查了学生对于分数意义中“平均分”这个要素的理解。
21.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】医生需要监测病人的体温情况,应选用折线统计图。
故答案为:√
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
22.9;25;3.5;;
;2;;
【详解】略
23.(1)137;(2)
【分析】(1)根据乘法分配律,把算式转化为13.7×(9.9+0.1),进行计算;
(2)根据运算顺序,先算小括号里面的乘法,再算小括号里面的减法,最后算括号外面的加法。
【详解】(1)13.7×9.9+13.7×0.1
=13.7×(9.9+0.1)
=13.7×10
=137
(2)+(1-)
=+(1-)
=+
=
24.(1);(2)2
【分析】(1)先化简方程,再根据等式的性质,方程两边同时除以计算即可;
(2)根据比例的基本性质,原方程改写成x×=×8,再化简方程,最后根据等式的性质,方程两边同时除以计算即可。
【详解】(1)x-x=
解:
x=
(2)x∶=8∶
解:x×=×8
x=
x÷=÷
x=2
25.18元
【分析】把原来的价格看作单位“1”,增加了二成后现价是原价的(1+20%),求一个数的百分之几是多少,然后用乘法计算即可。
【详解】二成就是百分之二十。
15×(1+20%)
=15×1.2
=18(元)
答:现在每升油18元。
【点睛】本题考查了百分数乘法应用题,关键是确定单位“1”,解答依据是:求一个数的百分之几是多少,用乘法计算。
26.8小时
【分析】首先根据速度×时间=路程,用去时的速度乘所用的时间,求出两地之间的距离是多少;然后根据路程÷速度=时间,用两地之间的距离除以返回的速度,求出从原路返回时需行多少小时即可。
【详解】72×10÷90
=720÷90
=8(小时)
答:8小时能够返回原地。
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
27.80米
【分析】甲乙两队所用的时间比是5∶7,根据工作总量=工作效率×工作时间可知,修这条路的工作量是一定的,工作效率和工作时间的乘积是一定的,说明工作效率和工作时间是成反比例的,所以两队同时修这条路,完成时所修的长度比是7∶5。把这条路的长度平均分成(7+5)份,先用除法求出1份的长度,再用乘法求出(7-5)份的长度,即甲队比乙队多修的米数。
【详解】480÷(7+5)×(7-5)
=480÷12×2
=80(米)
答:甲队比乙队多修80米。
【点睛】此题的解题关键是明白速度和时间是成反比例的,然后根据按比例分配问题解答。
28.10次
【详解】略
29.4厘米
【分析】根据题意,平行四边形BCEF与长方形ABCD同底等高,所以平行四边形BCEF的面积等于长方形ABCD的面积,根据平行四边形的面积公式可计算出平行四边形BCEF的面积,三角形BCG的面积等于平行四边形BCEF的面积减去阴影部分的面积,再根据三角形的面积公式计算出线段CG的长,可用CD的长减去CG的长就是DG的长,根据三角形的面积公式和平行四边形的面积公式列式解答即可得到答案。
【详解】三角形BCG的面积为:
8×12-64
=96-64
=32(平方厘米)
CG的长为:32×2÷8=8(厘米)
DG的长为∶12-8=4(厘米)
答:组合图形中DG的长为4厘米。
【点睛】此题主要考查的是平行四边形的面积公式和三角形的面积公式的应用。
30.(1)2∶1;(2)12.1公顷
【分析】(1)首先计算出向日葵的百分比,再求比值化简即可;
(2)根据花生的种植面积是6.6公顷,以及花生所占百分比,可以求出总的种植面积,再乘大豆与芝麻的种植面积的百分比即可。
【详解】(1)1-35%-30%-20%=15%
30%∶15%=2∶1
(2)6.6÷30%×(35%+20%)
=6.6÷0.3×0.55
=12.1(公顷)
答:大豆与芝麻的种植面积一共是12.1公顷。
【点睛】已知部分量求单位“1”用除法;已知单位“1”求部分量用乘法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考易错题检测卷(试题)2023-2024学年数学六年级下册人教版
一、选择题
1.下列展开图中,( )不能围成正方体。
A. B.
C. D.
2.玥玥家在学校西偏南40°方向上,那么学校在玥玥家( )方向上。
A.南偏西40° B.东偏北40° C.北偏东40° D.西偏南40°
3.华联超市五月份购进480kg大米,_____,该超市购进的面粉有多少千克?列式为:480÷(1+20%)。应选择的已知条件是( )。
A.购进的大米比面粉多20%
B.购进的大米比面粉少20%
C.购进的面粉比大米多20%
D.购进的面粉比大米少20%
4.红红以直线上点A为起点,先向东走5格,再向西走7格,移动后红红所在的位置可以用( )表示。
A.1 B.﹣5 C.﹣1 D.0
5.,x,y,z三个数相比较,最小的一个数是( )。
A.x B.y C.z D.无法判断
6.把一个长5厘米,宽4厘米的长方形按3∶1放大,放大后图形的面积是( )平方厘米。
A.54 B.60 C.70 D.180
7.一个圆柱与一个圆锥体积相等,底面积也相等,圆柱的高是12cm,圆锥的高是( )cm。
A.12 B.24 C.36 D.4
8.某品牌饮料搞促销活动,甲商场满100元减20元;乙商场一律打八折;丙商场买十送二。该饮料在三个商场的单价都是8元,李阿姨要买36瓶该品牌饮料,( )更省钱。
A.甲商场 B.乙商场 C.丙商场 D.无法确定谁
二、填空题
9.一匹布可以做8件上衣或10条裤子。现已做了1条裤子,剩下的要成套做可以做( )套。
10.有一个质数,它既是两个质数的和,又是两个质数的差,这个质数是( )。
11.A、B、C、D、E五人进行乒乓球比赛,每两个人都要赛一场。现在A、D赛了4场,B、C各自赛了3场,E至少赛( )场。
12.学生甲在一列队伍的排尾以每小时6千米的速度赶到队伍排头后,又以同样的速度返回队尾,一共用了3小时,若队伍进行的速度为每小时4千米,则队伍长为( )千米。
13.一瓶酒精,第一次倒出,然后倒回瓶中40克;第二次倒出瓶中剩下部分的。第三次倒出270克,瓶中还剩80克。原来瓶中有( )克。
14.对于任意自然数a、b,如果a*b=2a+6b,已知,那么x=( )。
15.一项工程,甲单独做需要10天,乙单独做需要15天,丙的工效比甲低但比乙高,三人合作最少需要( )天。(结果取整数)
16.甲、乙两个圆柱形容器,底面积比为6∶4,甲容器中水深18厘米,乙容器中水深12厘米,再往两个容器中注入同样多的水,使得两个容器中水一样深,这时水深( )厘米。
三、判断题
17.一筐苹果比一筐梨重20%,那么一筐梨就比一筐苹果轻20%。( )
18.X和Y表示两种变化的相关联的量,同时5X—7Y=0,X和Y不成比例.( )
19.小芳今年a岁,妈妈今年b岁,5年后妈妈比小芳大(b-a+5)岁。( )
20.把一根米长的绳子分成5段,每段占全长的。( )
21.医生需要监测病人的体温情况,应选用折线统计图。( )
四、计算题
22.直接写出结果。
×24= 15÷= 4.2×= ÷=
1÷= ÷= -= ÷×=
23.脱式计算。
(1)13.7×9.9+13.7×0.1 (2)+(1-)
24.解方程(或比例)。
(1)x-x= (2)x∶=8∶
五、解答题
25.一种食品油,由于成本提高,现在每升比原来的价格增加了二成,原来每升油15元,现在每升油多少元?
26.一辆运货汽车从甲地到乙地,平均每小时行72千米,10小时到达。回来时空车原路返回,每小时可行90千米。多长时间能够返回原地?
27.修一条长480米的路,如果单独修完,甲乙两队所用的时间比是5∶7,现在让两队同时修这条路,完成时,甲队比乙队多修多少米?
28.一个圆锥形的煤堆,占地50m2,高2.4m.如果每立方米煤重1.5t,用一辆载质量为6t的卡车来运,至少几次能全部运完?
29.如图,在长方形ABCD中,厘米,厘米,平行四边形BCEF的一边BF交CD于点G,若梯形CEFG的面积为64平方厘米,则DG的长为多少?
30.滨海村各种作物种植面积的分布情况如图所示,请根据统计图回答以下问题:
(1)花生的种植面积与向日葵种植面积的最简单的整数比是( )。
(2)如果花生的种植面积是6.6公顷,那么大豆与芝麻的种植面积一共是多少公顷?(列式解答)
参考答案:
1.C
【分析】根据正方体展开图的11种特征,即可确定哪个图形属于正方体展开图,能围成正方体,哪个图形不属于正方体展开图,不能围成正方体。据此解答。
【详解】A.属于正方体展开图的“1-4-1”型,能围成正方体;
B.属于正方体展开图的“2-2-2”型,能围成正方体;
C.不属于正方体展开图,不能围成正方体。
D.属于正方体展开图的“1-3-2”型,能围成正方体。
故答案为:C
【点睛】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
2.B
【分析】根据方向的相对性:方向相反,角度不变;据此解题即可。
【详解】根据方向的相对性可得:玥玥家在学校西偏南40°方向上,那么学校在玥玥家东偏北40°方向上。
故答案为:B
【点睛】本题主要考查了方向,注意方向的相对性。
3.A
【分析】算式使用除法和加法解答,求的是单位“1”,因此应当是比单位“1”(面粉的质量)多20%;据此解答即可。
【详解】由分析可得:应选择的已知条件是购进的大米比面粉多20%。
故答案为:A
【点睛】本题考查了百分数除法应用题,关键是确定单位“1”,找到具体数量对应的百分率;解答依据是:已知一个数的百分之几是多少,求这个数,用除法计算。
4.C
【分析】在一对具有相反意义的量中,向东为正,向西为负,根据题干,结合数轴起点A的位置进行解答即可。
【详解】由分析可得:移动后红红所在的位置可以用﹣1表示。
故答案为:C
【点睛】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
5.C
【分析】三个算式的和相等,利用异分母异分子分数比较大小的方法,比较出三个算式中的数字加数的大小,就可以比较出三个字母的大小。
【详解】,,
可得;
且,所以x>y>z。
故答案为:C
【点睛】两个加法算式的和相等,如果甲算式中的一个加数大于乙算式的一个加数,则甲算式中的另一个加数一定小于乙算式的另一个加数。
6.D
【分析】根据题意,把长、宽按3∶1放大,先分别求出放大后的长、宽各是多少厘米,再根据长方形的面积公式:S=ab,把数据代入公式求出放大后的面积,即可进行解答。
【详解】放大后的长:5×3=15(厘米)
放大后的宽:4×3=12(厘米)
放大后图形的面积:15×12=180(平方厘米)
所以,放大后的面积是180平方厘米。
故答案为:D
【点睛】解答此题首先求出放大后的长、宽,再根据长方形的面积公式解答即可。
7.C
【分析】根据圆柱的体积公式,圆锥的体积公式,当圆柱和圆锥的体积、底面积分别相等时,圆锥的高是圆柱的高的3倍,由此求出圆锥的高,进而做出选择。
【详解】(cm)
故答案为:C
【点睛】此题主要考查了利用圆柱与圆锥的体积公式,推导出在体积、底面积分别相等时,圆柱的高与圆锥的高的关系。
8.B
【分析】甲商场:100元减20元现金,用总价减去减的现金即可求出要花的钱;乙商场:乙商场打八折,是指现价是原价的80%,根据单价×数量=总价,即可求出一共用多少元;丙商场:先求出买36个可以送几个,再根据实际买的个数乘单价求出花的钱数;比较即可求出哪家商场更省钱。
【详解】36×8-20
=288-20
=268(元)
8×80%×36
=6.4×36
=230.4(元)
36÷(10+2)
=36÷12
=3(组)
3×2=6(个)
(36-6)×8
=30×8
=240(元)
230.4<240<268
故答案为:B
【点睛】本题关键是根据各个商场不同的优惠方法求出每个商场要花的钱,通过比较得出哪个商场便宜。
9.4
【分析】把总布料看作单位“1”,用分数表示做一件上衣和一条裤子用的布料各占总布料的分率,剩下的布料可以做的套数=剩下布料占总布料的分率÷做一套衣服用去的布料占总布料的分率,据此解答。
【详解】假设总布料为1。
(1-)÷(+)
=÷
=4(套)
所以,剩下的要成套做可以做4套。
【点睛】本题主要考查分数除法的应用,求出做一套衣服需要的布料占总布料的分率是解答题目的关键。
10.5
【分析】所有的质数中2是唯一的偶质数,除2以外所有的质数都是奇数,那么这个质数一定是奇数,奇数与奇数的和(差)一定是偶数,奇数与偶数的和(差)一定是奇数,则这个质数的和或差中一定有一个质数是2,据此解答。
【详解】分析可知,和或差中有一个质数为2,2+3=5,7-2=5,2、3、5、7都是质数,符合题意,所以这个质数是5。
【点睛】掌握奇数和偶数的运算性质是解答题目的关键。
11.2
【分析】五人进行乒乓球比赛,每两个人都要赛一场,即每人都要和另外四个人赛一场,共赛4场。现在A、D都赛了4场,即A和D和除了自己以外的其它四人都赛了一场,B、C都赛了3场,则B这三场可和A、C、D各赛一场,C可和A、B、D各赛一场,所以E至少赛了2场,即和A、D各赛一场。
【详解】根据分析得,E至少赛2场。
【点睛】根据每人需要比赛的总场数及A、B、C、D已赛的场数进行推理分析,从而得出结论是完成本题的关键。
12.5
【分析】设这列队伍的长为x千米,此过程分两段,第一段是从队尾到排头的追及问题,此段所用的时间是小时,第二段是从排头到队尾的相遇问题,此段所用的时间是小时,一共用了3小时。根据等量关系:从队尾到排头的时间+从排头到队尾的时间=行走的时间,再列方程解答。
【详解】解:设这列队伍的长为x千米。
+=3
+=3
+=3
=3
x=3÷
x=5
即队伍长5千米。
【点睛】本题解题关键是理解“从队尾到排头的追及问题,从排头到队尾的相遇问题”,根据题目中的等量关系,再列方程解答。
13.885
【分析】第二次到出剩下酒精的,这时还剩下的(270+80)克,就是剩下酒精的(1-),求出第二次倒出前剩下的再减去40,就是全部酒精的(1-),据此解答。
【详解】(270+80)÷(1-)
=350÷
=630(克)
(630-40)÷(1-)
=590÷
=885(克)
【点睛】本题的关键是先求出第二次倒出前剩下酒精的重量。
14.896
【分析】定义新运算的一般解题步骤:
(1)关键问题:审题。正确理解定义的运算符号的意义。
(2)严格按照新定义的计算顺序,将数值代入算式中,准确找出要计算的习题中数据与定义中字母的对应关系,把它转化为一般的四则运算。
据此将转化成方程,求解即可。
【详解】
解:
【点睛】新的运算有自己的特点,适用于加法和乘法的运算定律不一定适用于定义运算,要特别注意运算顺序。
15.4
【分析】甲的工作效率是,乙的工作效率是,要想使三人合作天数最少,丙的工作效率就要尽可能的高,则丙的工作效率是,将工作总量看作单位“1”,1÷工作效率和=工作天数,据此分析。
【详解】1÷(++)
=1÷
≈4(天)
【点睛】关键是理解工作效率、工作时间、工作总量之间的关系,时间分之一可以看作效率。
16.30
【分析】根据体积相等时,圆柱的底面积和高成反比,底面积比为6:4,那么注入同体积的水的深度比是4:6,可设这时水深为x厘米,根据水的深度比,列出方程即可解答。
【详解】解:设这时水深为x厘米。
【点睛】本题主要考查圆柱的体积公式的灵活运用,列出方程解决问题是比较直观的方法。
17.×
【分析】假设一筐梨的重量是“1”,则苹果的重量是梨质量的(1+20%)=120%,求一筐梨比一筐苹果轻百分之几,用20%除以120%计算即可。
【详解】20%÷(1+20%)×100%
=0.2÷1.2×100%
≈16.7%
一筐梨比一筐苹果轻16.7%,原题说法错误。
故答案为:×
【点睛】此题重点考查学生对单位“1”的确定,找准不同的单位“1”是解决此题的关键。
18.×
【分析】根据正反比例的意义,分析数量关系,找出一定的量,然后看那两个变量是比值一定还是乘积一定,从而判定成什么比例关系.
【详解】因为5x﹣7y=0,
所以5x=7y,x:y=1.4(一定),
可以看出,x和y是两种相关联的量,x随y的变化而变化,
1.4是一定的,也就是x与y相对应数的比值一定,符合正比例的意义.
所以x与y成正比例关系.
19.×
【分析】因为年龄差始终不变,所以今年的年龄差就是5年后的年龄差,用减法求出两人今年的年龄差即可。
【详解】两人的年龄差不变,都是:(b a)岁
故答案为:×
【点睛】解题关键是明确年龄差是一个不变量,求出今年的年龄差即可。
20.×
【分析】把一根米长的绳子看作一个整体,把它平均分成5份,其中的1份用分数表示是。
【详解】把一根米长的绳子平均分成5段,每段占全长的,原题缺少“平均”两字。
故答案为:×
【点睛】本题重点考查了学生对于分数意义中“平均分”这个要素的理解。
21.√
【分析】条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【详解】医生需要监测病人的体温情况,应选用折线统计图。
故答案为:√
【点睛】此题应根据条形统计图、折线统计图、扇形统计图各自的特点进行解答。
22.9;25;3.5;;
;2;;
【详解】略
23.(1)137;(2)
【分析】(1)根据乘法分配律,把算式转化为13.7×(9.9+0.1),进行计算;
(2)根据运算顺序,先算小括号里面的乘法,再算小括号里面的减法,最后算括号外面的加法。
【详解】(1)13.7×9.9+13.7×0.1
=13.7×(9.9+0.1)
=13.7×10
=137
(2)+(1-)
=+(1-)
=+
=
24.(1);(2)2
【分析】(1)先化简方程,再根据等式的性质,方程两边同时除以计算即可;
(2)根据比例的基本性质,原方程改写成x×=×8,再化简方程,最后根据等式的性质,方程两边同时除以计算即可。
【详解】(1)x-x=
解:
x=
(2)x∶=8∶
解:x×=×8
x=
x÷=÷
x=2
25.18元
【分析】把原来的价格看作单位“1”,增加了二成后现价是原价的(1+20%),求一个数的百分之几是多少,然后用乘法计算即可。
【详解】二成就是百分之二十。
15×(1+20%)
=15×1.2
=18(元)
答:现在每升油18元。
【点睛】本题考查了百分数乘法应用题,关键是确定单位“1”,解答依据是:求一个数的百分之几是多少,用乘法计算。
26.8小时
【分析】首先根据速度×时间=路程,用去时的速度乘所用的时间,求出两地之间的距离是多少;然后根据路程÷速度=时间,用两地之间的距离除以返回的速度,求出从原路返回时需行多少小时即可。
【详解】72×10÷90
=720÷90
=8(小时)
答:8小时能够返回原地。
【点睛】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握。
27.80米
【分析】甲乙两队所用的时间比是5∶7,根据工作总量=工作效率×工作时间可知,修这条路的工作量是一定的,工作效率和工作时间的乘积是一定的,说明工作效率和工作时间是成反比例的,所以两队同时修这条路,完成时所修的长度比是7∶5。把这条路的长度平均分成(7+5)份,先用除法求出1份的长度,再用乘法求出(7-5)份的长度,即甲队比乙队多修的米数。
【详解】480÷(7+5)×(7-5)
=480÷12×2
=80(米)
答:甲队比乙队多修80米。
【点睛】此题的解题关键是明白速度和时间是成反比例的,然后根据按比例分配问题解答。
28.10次
【详解】略
29.4厘米
【分析】根据题意,平行四边形BCEF与长方形ABCD同底等高,所以平行四边形BCEF的面积等于长方形ABCD的面积,根据平行四边形的面积公式可计算出平行四边形BCEF的面积,三角形BCG的面积等于平行四边形BCEF的面积减去阴影部分的面积,再根据三角形的面积公式计算出线段CG的长,可用CD的长减去CG的长就是DG的长,根据三角形的面积公式和平行四边形的面积公式列式解答即可得到答案。
【详解】三角形BCG的面积为:
8×12-64
=96-64
=32(平方厘米)
CG的长为:32×2÷8=8(厘米)
DG的长为∶12-8=4(厘米)
答:组合图形中DG的长为4厘米。
【点睛】此题主要考查的是平行四边形的面积公式和三角形的面积公式的应用。
30.(1)2∶1;(2)12.1公顷
【分析】(1)首先计算出向日葵的百分比,再求比值化简即可;
(2)根据花生的种植面积是6.6公顷,以及花生所占百分比,可以求出总的种植面积,再乘大豆与芝麻的种植面积的百分比即可。
【详解】(1)1-35%-30%-20%=15%
30%∶15%=2∶1
(2)6.6÷30%×(35%+20%)
=6.6÷0.3×0.55
=12.1(公顷)
答:大豆与芝麻的种植面积一共是12.1公顷。
【点睛】已知部分量求单位“1”用除法;已知单位“1”求部分量用乘法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
