数学高中人教A版必修一2.2.2 对数函数及其性质课件(22张)
文档属性
| 名称 | 数学高中人教A版必修一2.2.2 对数函数及其性质课件(22张) |  | |
| 格式 | zip | ||
| 文件大小 | 394.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-20 22:07:40 | ||
图片预览






文档简介
课件22张PPT。§2.2.2对数函数及其性质 教学目标 过程与方法:通过对对数函数及其性质的研究与学习,体会新知识的形成过程,体会其中蕴含的归纳、类比、数形结合、分类讨论等数学方法和思想。知识与技能:熟练应用指数对数的互化、对数的运算、体会对数和指数的辩证统一。情感态度与价值观:让学生在探究新知识的过程中,充分体验数学方法、数学思想,体会数学的应用价值。 重 点 难 点重点:对数函数的图像和性质难点:对数函数图像和性质的
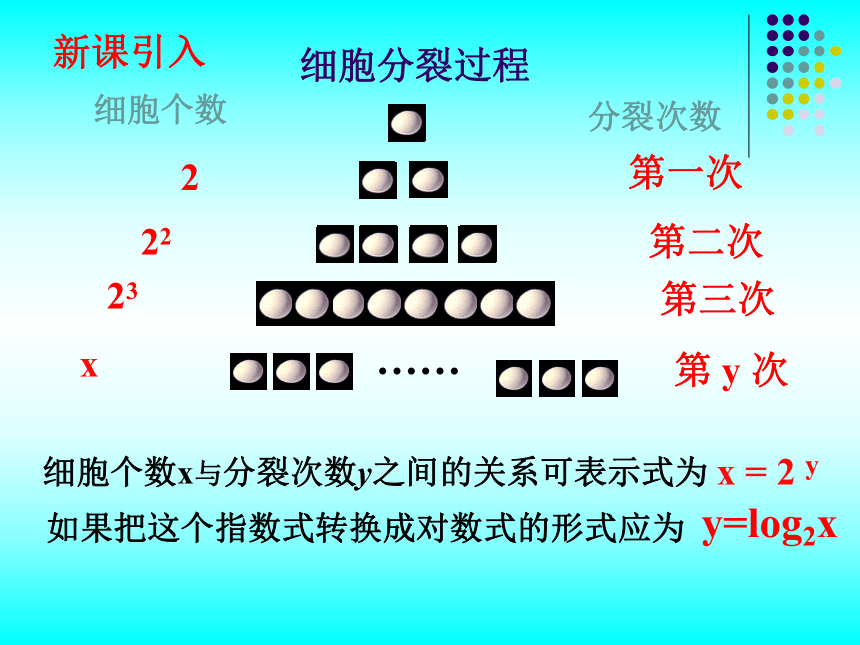
知识形成过程及应用复习: 一般地,函数 y = ax ( a > 0, 且 a ≠ 1 ) 叫做指数函数,其中x是自变量.a > 10 < a < 1 图 象 性 质定 义 域 : 值 域 :过 点 ( 0 , 1 ) ,即 x = 0 时, y = 1 . 在R 上是增函数在 R上是减函数R(0 , +∞)复习回顾新课引入细胞分裂过程第一次第二次第三次第 y 次……细胞个数x与分裂次数y之间的关系可表示式为x = 2 y
如果把这个指数式转换成对数式的形式应为y=log2x 分裂次数细胞个数222x23判断函数是否为对数函数要看三点
1、底数 a>0且a≠1
2、真数为单个自变量x
3、系数为1
(1)
(2)
(3)
(4)
练习:判断下列关于x的函数那些是对数函数?在同一坐标系中用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
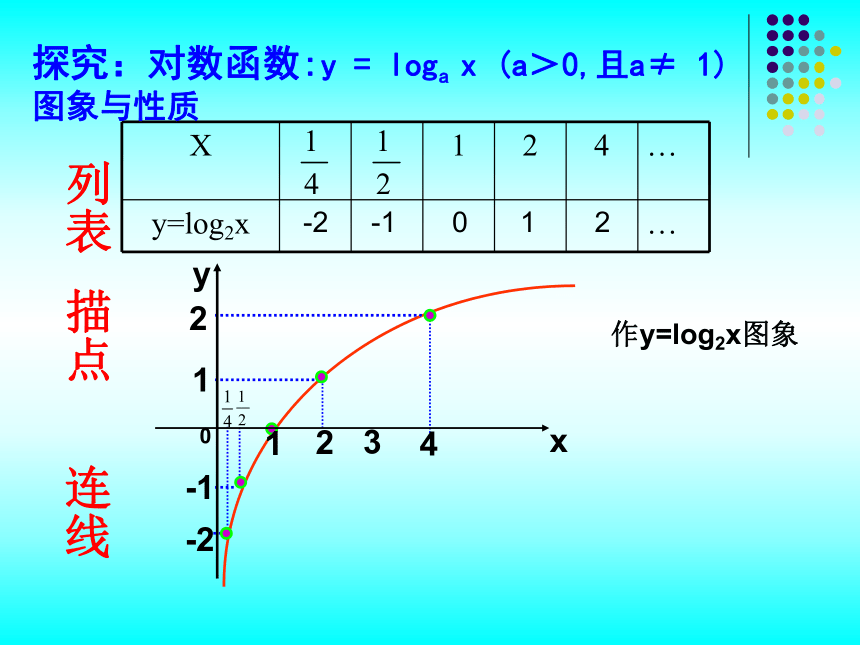
③用平滑曲线连接。性质探究探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质列表描点作y=log2x图象连线探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质-2-1012列表描点连线 2 1 0 -1 -2 -2 -1 0 1 2 … … … … … … 探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质对数函数 的图象。猜猜: 0(1, 0)·(1, 0)0增函数 减函数过点(1,0),即 一般地,对数函数y=logax在a>1及0(0,+∞)R过点(1,0),即x=1时y=0在(0,+∞)上是增函数在(0,+∞)上是减函数当0<x<1时,y<0
当x=1时,y=0
当x>1时,y>0当0<x<1时,y>0
当x=1时,y=0
当x>1时,y<0例1:求下列函数的定义域:
①y=logax2 ②y=loga(4-x) 分析:求函数定义域,必须使函数有意义,对本题而言,即要求对数式的真数大于0解: ②要使函数有意义 则4-x>0即x<4 所以该函数的定义域是 {x│x<4} 探究:求函数 的定义域 解:要使函数有意义则解得所以函数的定义域为方法归纳:
1、对数式的真数部分必须大于0
2、对数式的底数必须大于0且不等于1.跟踪练习:求下列函数的定义域例2 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )解:
⑴对于对数函数 y = log 2x,
因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log 23.4<log 28.5⑵对于对数函数 y = log 0.3 x,
因为它的底数为0.3,而0<0.3<1,所以
它在(0,+∞)上是减函数,于是
log 0.31.8>log 0.32.7⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )解:
当a>1时,函数y=log ax在(0,+∞)
上是增函数,于是
log a5.1<log a5.9 当0<a<1时,函数y=log ax在 (0,+∞)上是减函数,于是
log a5.1>log a5.9方法归纳
(1)如果底数相同,可以利用对数函数的单调性比较两个对数的大小
(2)对底数a与1的大小关系未明确指出时,要对底数进行分类讨论来
比较两个对数的大小.
(3)注意数形结合思想的应用例题讲解 练习: 比较下列各题中两个值的大小:⑴ log106 log108⑵ log0.56 log0.54 (3)log1.51.6 log1.51.4<<>当堂检测1、对数函数的图像过点(4,2),则 f(2)=___2、函数 的定义域为( )
A.(2,5) B.[2,5] C. D.3、已知 ,则 的大小关系是 。1Cm>n课堂小结一个函数两种题型三种思想作业布置(书面作业)
课本P74 7、8题(课外思考)
探究:若 ,则a
的取值范围是什么?
若 呢?
知识形成过程及应用复习: 一般地,函数 y = ax ( a > 0, 且 a ≠ 1 ) 叫做指数函数,其中x是自变量.a > 10 < a < 1 图 象 性 质定 义 域 : 值 域 :过 点 ( 0 , 1 ) ,即 x = 0 时, y = 1 . 在R 上是增函数在 R上是减函数R(0 , +∞)复习回顾新课引入细胞分裂过程第一次第二次第三次第 y 次……细胞个数x与分裂次数y之间的关系可表示式为x = 2 y
如果把这个指数式转换成对数式的形式应为y=log2x 分裂次数细胞个数222x23判断函数是否为对数函数要看三点
1、底数 a>0且a≠1
2、真数为单个自变量x
3、系数为1
(1)
(2)
(3)
(4)
练习:判断下列关于x的函数那些是对数函数?在同一坐标系中用描点法画出对数函数
的图象。作图步骤: ①列表,
②描点,
③用平滑曲线连接。性质探究探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质列表描点作y=log2x图象连线探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质-2-1012列表描点连线 2 1 0 -1 -2 -2 -1 0 1 2 … … … … … … 探究:对数函数:y = loga x (a>0,且a≠ 1) 图象与性质对数函数 的图象。猜猜: 0(1, 0)·(1, 0)0增函数 减函数过点(1,0),即 一般地,对数函数y=logax在a>1及0
当x=1时,y=0
当x>1时,y>0当0<x<1时,y>0
当x=1时,y=0
当x>1时,y<0例1:求下列函数的定义域:
①y=logax2 ②y=loga(4-x) 分析:求函数定义域,必须使函数有意义,对本题而言,即要求对数式的真数大于0解: ②要使函数有意义 则4-x>0即x<4 所以该函数的定义域是 {x│x<4} 探究:求函数 的定义域 解:要使函数有意义则解得所以函数的定义域为方法归纳:
1、对数式的真数部分必须大于0
2、对数式的底数必须大于0且不等于1.跟踪练习:求下列函数的定义域例2 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )解:
⑴对于对数函数 y = log 2x,
因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log 23.4<log 28.5⑵对于对数函数 y = log 0.3 x,
因为它的底数为0.3,而0<0.3<1,所以
它在(0,+∞)上是减函数,于是
log 0.31.8>log 0.32.7⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )解:
当a>1时,函数y=log ax在(0,+∞)
上是增函数,于是
log a5.1<log a5.9 当0<a<1时,函数y=log ax在 (0,+∞)上是减函数,于是
log a5.1>log a5.9方法归纳
(1)如果底数相同,可以利用对数函数的单调性比较两个对数的大小
(2)对底数a与1的大小关系未明确指出时,要对底数进行分类讨论来
比较两个对数的大小.
(3)注意数形结合思想的应用例题讲解 练习: 比较下列各题中两个值的大小:⑴ log106 log108⑵ log0.56 log0.54 (3)log1.51.6 log1.51.4<<>当堂检测1、对数函数的图像过点(4,2),则 f(2)=___2、函数 的定义域为( )
A.(2,5) B.[2,5] C. D.3、已知 ,则 的大小关系是 。1Cm>n课堂小结一个函数两种题型三种思想作业布置(书面作业)
课本P74 7、8题(课外思考)
探究:若 ,则a
的取值范围是什么?
若 呢?
