2023-2024学年高二数学下学期苏教版2019期末模拟测试卷(含解析)
文档属性
| 名称 | 2023-2024学年高二数学下学期苏教版2019期末模拟测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 20:33:01 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年高二数学下学期苏教版2019期末模拟测试卷
考试范围:选择性必修第二册
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知随机变量,若,则( )
A.0.2 B.0.3 C.0.7 D.0.8
2.如图,在正三棱柱中,,P为的中点,则( )
A. B.1 C. D.
3.已知一系列样本点的一个经验回归方程为,若样本点的残差为1,则( )
A. B.6 C. D.8
4.已知空间向量,则向量在向量上的投影向量是( )
A. B. C. D.
5.已知,随机变量的分布列为
4 6 8
设,则( )
A.数列单调递增 B.数列单调递减
C.数列先增后减 D.数列先减后增
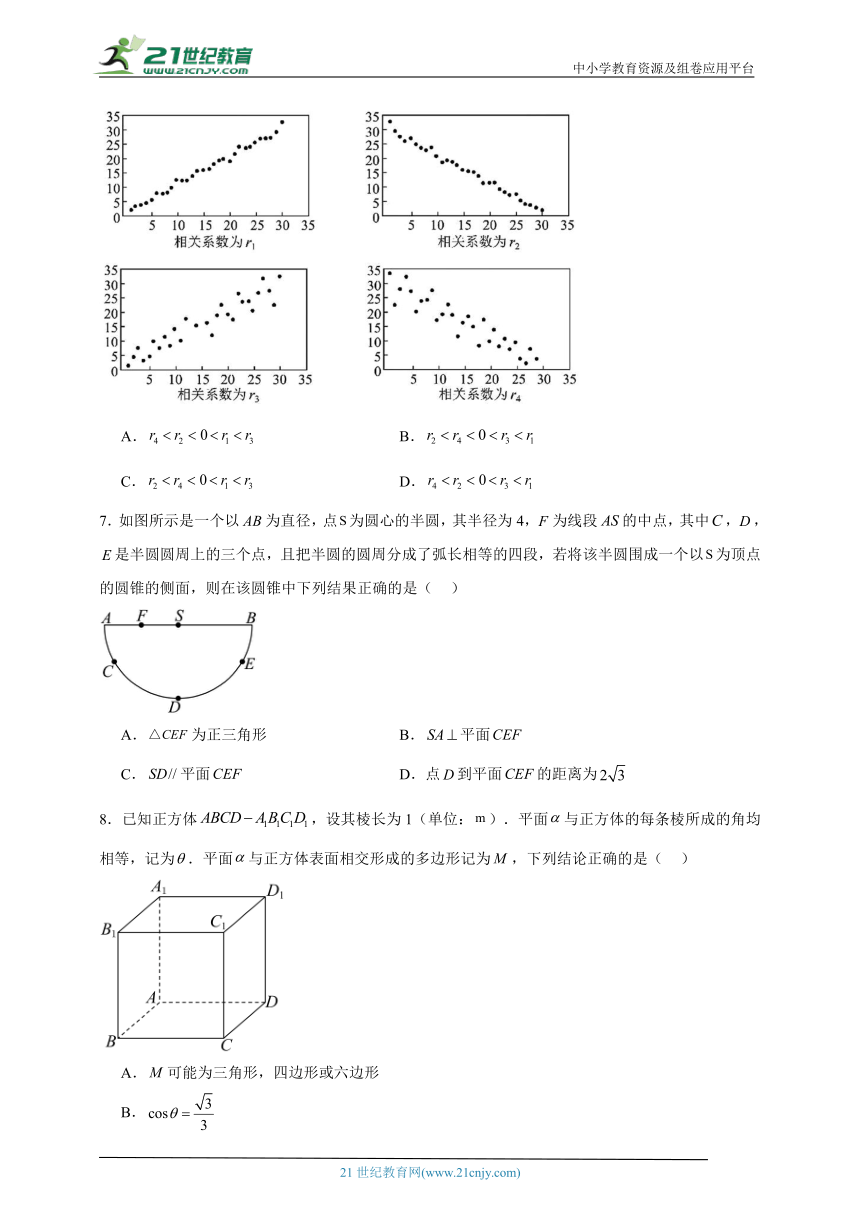
6.对四组数据进行统计,获得如图散点图,关于其相关系数的比较,正确的是( )
A. B.
C. D.
7.如图所示是一个以为直径,点为圆心的半圆,其半径为4,为线段的中点,其中,,是半圆圆周上的三个点,且把半圆的圆周分成了弧长相等的四段,若将该半圆围成一个以为顶点的圆锥的侧面,则在该圆锥中下列结果正确的是( )
A.为正三角形 B.平面
C.平面 D.点到平面的距离为
8.已知正方体,设其棱长为1(单位:).平面与正方体的每条棱所成的角均相等,记为.平面与正方体表面相交形成的多边形记为,下列结论正确的是( )
A.可能为三角形,四边形或六边形
B.
C.的面积的最大值为
D.正方体内可以放下直径为的圆
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.的展开式中,下列结论正确的是( )
A.展开式共7项 B.含项的系数为480
C.无常数项 D.所有项的二项式系数之和为128
10.下列说法正确的是( )
A.若回归方程为,则变量x与y负相关
B.运用最小二乘法求得的经验回归直线方程一定经过样本点的中心
C.若散点图中所有点都在直线上,则相关系数
D.若决定系数的值越接近于1,表示回归模型的拟合效果越好
11.如图,平面,,,,,,,则( )
A.
B.平面
C.平面与平面的夹角的余弦值为
D.直线与平面所成角的正弦值为
三、填空题:本题共3小题,每小题5分,共15分.
12.五种活动,甲、乙都要选择三个活动参加.甲选到的概率为 ;已知乙选了活动,他再选择活动的概率为 .
13.设,若,且,则 .
14.如图,在长方体中,已知,.动点P从出发,在棱上匀速运动;动点Q同时从B出发,在棱BC上匀速运动,P的运动速度是Q的两倍,各自运动到另一端点停止.它们在运动过程中,设直线PQ与平面ABCD所成的角为,则的取值范围是 .
四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、证明过程或演算步骤.
15.现有4名男生和3名女生,
(1)若安排7名学生站成一排照相,要求甲乙排在一起,这样的排法有多少种?
(2)若安排7名学生站成一排照相,要求3名女生互不相邻,这样的排法有多少种?
(3)若邀请7名学生中的4名参加一项活动,其中男生甲和女生乙不能同时参加,求邀请的方法种数.
16.一个质点在随机外力的作用下,从平面直角坐标系的原点出发,每隔1秒等可能地向上 向下 向左或向右移动一个单位.
(1)共移动两次,求质点与原点距离的分布列和数学期望;
(2)分别求移动4次和移动6次质点回到原点的概率;
(3)若共移动次(大于0,且为偶数),求证:质点回到原点的概率为.
17.已知四棱柱中,底面为梯形,,平面,,其中.是的中点,是的中点.
(1)求证平面;
(2)求平面与平面的夹角余弦值;
(3)求点到平面的距离.
18.为了研究学生的性别与是否喜欢运动的关联性,随机调查了某中学的100名学生,整理得到如下列联表:
男学生 女学生 合计
喜欢运动 40 20 60
不喜欢运动 20 20 40
合计 60 40 100
(1)依据的独立性检验,能否认为学生的性别与是否喜欢运动有关联?
(2)按学生的性别以及是否喜欢运动用分层随机抽样的方法从这100名学生中选取10人,再从这10人中任选2人,求至少有1名喜欢运动的男学生被选中的概率.
附:,其中.
0.1 0.05 0.01
2.706 3.841 6.635
19.如图1,在梯形中,,是线段上的一点,,,将沿翻折到的位置.
(1)如图2,若二面角为直二面角,,分别是,的中点,若直线与平面所成角为,,求平面与平面所成锐二面角的余弦值的取值范围;
(2)我们把和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线,点为线段的中点,,分别在线段,上(不包含端点),且为,的公垂线,如图3所示,记四面体的内切球半径为,证明:.
参考答案:
1.D
【分析】利用正态分布的对称性求概率.
【详解】随机变量,,
则,
故.
故选:D.
2.A
【分析】以为基底表示后可求的值.
【详解】由正三棱柱可得,,
而,
故
,
故选:A.
3.C
【分析】观测值减去预测值称为残差;进而利用残差的定义即可求解.
【详解】样本点的观测值为,预测值为,
则残差为,解得.
故选:C.
4.A
【分析】根据向量投影的概念,结合向量的数量积计算得出结果.
【详解】根据题意,, ,,
在上的投影向量可为
故选:A.
5.A
【分析】先由公式求出,得到,由函数性质得到的单调性.
【详解】,,
当,时,数列单调递增.
故选:A.
6.B
【分析】根据散点图和相关系数的概念和性质辨析即可.
【详解】由散点图可知,相关系数所在散点图呈负相关,所在散点图呈正相关,所以都为正数,都为负数.
所在散点图近似一条直线上,线性相关性比较强,相关系数的绝对值越接近,
而所在散点图比较分散,线性相关性比较弱点,相关系数的绝对值越远离.
综上所得:.
故答案为:B.
7.C
【分析】根据题意,还原圆锥原图,找出对应线段长度关系,位置关系.很容易得解.
【详解】选项A,该半圆围成的圆锥,如图所示,
设圆锥底面半径为,则,∴,∴,
∵为的中点,为的中点,∴,且,
∴,为等腰直角三角形,选项A错误;
选项B,若平面,则,直角中,,
∴,选项B错误;
选项C,∵,∴平面,选项C正确;
选项D,∵,,∴平面,∴平面平面,
∴到直线的距离即为到平面的距离,
又∵,∴到直线的距离等于到直线的距离,为,选项D错误;
故选:C.
8.D
【分析】A选项,如图,建立以A为原点的空间直角坐标系,利用向量知识可知平面可为与垂直的平面,即可判断选项正误;B选项,由A选项分析及线面角计算公式可判断选项正误;C选项,由A选项分析可表示出两种情况下的面积表达式,即可判断选项正误;D选项,问题等价于判断内部最大圆直径最大值是否大于1.2.
【详解】A选项,如图,以A为原点建立空间直角坐标系,
则,
.
设平面法向量为,因平面与正方体的每条棱所成的角均相等,
则
.
由对称性,不妨取,则法向量可为,又,
则平面可为与垂直的平面.
如图,连接,
因平面ABCD,平面ABCD,
则,又平面,
则平面,又平面,则,同理可得.
又平面,,故平面.
即平面可为与平面平行的平面,
当平面与(不含A)相交时,M为与相似的正三角形;
当平面与(不含)相交时,M为如图所示的六边形;
当平面与相交时(不含),M为与相似的正三角形;
则可能为三角形,六边形,故A错误;
B选项,由A选项分析可知,,故B错误.
C选项,由A选项分析可知,当平面过或时,
所得正三角形面积最大,由题可得边长为,则相应面积为.
当为六边形时,如下图所示,因,,又,
结合图形可知,又由题可知六边形为中心对称图形,
取其对称中心为O,则四边形四边形四边形,
则六边形面积为相应四边形面积的3倍.取RS,RT中点分别为F,E,
连接EF,OE,OF,因,则,
四边形面积为四边形面积2倍,则六边形面积为四边形面积6倍.
设,
由题结合图形可知, ,则
在中,由余弦定理,.
注意到,则四点共圆,
则外接圆直径等于OR,由正弦定理,可得.
则,.
则六边形面积S
,当且仅当时取等号.
又 ,则的面积的最大值为,故C错误;
D选项,先判断M内部的最大圆直径最大值是否超过1.2m.
当M为正三角形时,M内部的最大圆为三角形内切圆,
易知当平面过或时,所得内切圆半径最大,
设此时内切圆半径为,三角形面积为,周长为C,
则内切圆直径.
当M为六边形时,M内部的最大圆半径满足,
由C选项分析,可知,则当时,
取最大值,则此时M内部的最大圆直径的最大值为,
因,则,即正方体内可以放下直径为的圆,故D正确.
故选:D
【点睛】关键点睛:本题首先需要通过向量方法,得到满足题意的平面的具体特征,后利用几何知识,结合正余弦定理可得图形的面积最大值及其内部最大圆直径.
9.CD
【分析】根据题意,结合二项展开式的性质,以及展开式的通项公式和二项式系数的性质,逐项判定,即可求解.
【详解】对于A中,由二项式的展开式共有8项,所以A错误;
对于B中,由二项式,可得展开式的通项为,
令,可得,则展开式的项的系数为,所以B错误;
对于C中,由,令,可得,
所以展开式中没有常数项,所以C正确;
对于D中,由展开式的二项式系数的性质,可得展开式中所有二项式系数和为,所以D正确.
故选:CD.
10.ABD
【分析】利用正负相关的意义判断A;利用回归直线的性质判断B;利用相关系数、决定系数意义判断CD.
【详解】对于A,回归方程为的斜率为负,则变量x与y负相关,A正确;
对于B,回归直线方程一定经过样本点的中心,B正确;
对于C,散点图中所有点都在直线上,则相关系数,C错误;
对于D,决定系数的值越接近于1,表示回归模型的拟合效果越好,D正确.
故选:ABD
11.BC
【分析】建立空间直角坐标系,利用空间向量法一一计算可得.
【详解】因为平面,,
由题意,以为坐标原点,分别以,,的方向为轴、轴、轴正方向建立空间直角坐标系,
可得,,,,,,
则,,
所以,所以,不垂直,故A错误;
依题意,是平面的法向量,
又,可得,则,
又因为直线平面,所以平面,故B正确;
设为平面的一个法向量,则,
即,令,可得,
依题意,,,
设为平面的法向量,
则,即,不妨令,可得,
所以,
故平面与平面的夹角的余弦值为,故C正确;
设直线与平面所成角为,,
则,故D错误.
故选:BC.
12.
【分析】结合列举法或组合公式和概率公式可求甲选到的概率;采用列举法或者条件概率公式可求乙选了活动,他再选择活动的概率.
【详解】解法一:列举法
从五个活动中选三个的情况有:
,共10种情况,
其中甲选到有6种可能性:,
则甲选到得概率为:;
乙选活动有6种可能性:,
其中再选则有3种可能性:,
故乙选了活动,他再选择活动的概率为.
解法二:
设甲、乙选到为事件,乙选到为事件,
则甲选到的概率为;
乙选了活动,他再选择活动的概率为
故答案为:;
13.56
【分析】分析可知是二项式系数最大的唯一一项,由二项式系数的性质可得,即可得结果.
【详解】因为,
可知,
若,且,则是二项式系数最大的唯一一项,则,
所以.
故答案为:56.
14.
【分析】根据给定条件,建立空间直角坐标系,设,并求出的坐标,再结合线面角的向量求法求解.
【详解】在长方体中,以点为原点,建立如图所示的空间直角坐标系,
设,由P的运动速度是的2倍,得,即,
则,显然平面的法向量,
于是,
,因此,
显然当时,,当时,,
所以的取值范围是.
故答案为:
【点睛】关键点点睛:用向量法求直线与平面所成的角,求出平面的法向量是关键,并注意公式求出的是线面角的正弦.
15.(1)1440
(2)1440
(3)25
【分析】(1)利用捆绑法,结合排列组合知识求解;
(2)利用插空法,结合排列组合知识求解;
(3)利用间接法求解.
【详解】(1)由题意可知:运用捆绑法,可得共有排法数为种.
(2)由题意可知:运用插空法,可得共有排法数为种.
(3)由题意可知:邀请这7名学生中的4名参加一项活动共有种方法,
男生甲和女生乙同时参加的方法有,共有邀请方法数为种.
16.(1)答案见解析;
(2)
(3)证明见解析
【分析】(1)首先求出X的所有可能取值以及对应的概率,再结合离散型随机变量的期望公式求答案即可.
(2)利用分步乘法计数原理、组合以及古典概型的概率公式计算可求得结果.
(3)利用数学归纳法证明即可.
【详解】(1)设表示2次移动中质点与原点距离,则可取0,2,,
当质点向左移动1次向右移动1次,或向上移动1次向下移动1次,最后,则;
当质点向左移动2次或向右移动2次,或向上移动2次或向下移动2次,最后,则;
当质点向左移动1次向上移动1次,或向左移动1次向下移动1次,或向右移动1次向上移动1次,或向右移动1次向下移动1次,最后,则
的分布列为:
0
.
(2)质点从原点出发,每次等可能地向上 向下 向左或向右移动一个单位,共移动4次,
可能的结果共有种情况,
若质点回到原点,则向左移动2次向右移动2次,或向上移动2次向下移动2次,共有种情况,
若质点回到原点,则向左移动1次向右移动1次,向上移动1次向下移动1次,共有种情况,
所以质点回到原点的概率为.
质点从原点出发,每次等可能地向上 向下 向左或向右移动一个单位,共移动6次,
可能的结果共有种情况,
若质点回到原点,则向左移动3次向右移动3次,或向上移动3次向下移动3次,共有种情况,
若质点回到原点,则向左移动2次向右移动2次,向上移动1次向下移动1次,则向左移动1次向右移动1次,向上移动2次向下移动2次,共有种情况,
所以质点回到原点的概率为.
(3)若共移动2次,质点回到原点的概率为;
假设共移动N次,满足质点回到原点的概率为;
当共移动次,
移动N次质点回到原点当质点向左移动1次向右移动1次,或向上移动1次向下移动1次,移动次质点回到原点;
移动N次质点在,当质点向左移动2次或向右移动2次,或向上移动2次或向下移动2次,移动次质点回到原点;
移动N次质点在当质点向左移动1次向上移动1次,或向左移动1次向下移动1次,或向右移动1次向上移动1次,或向右移动1次向下移动1次,,移动N+2次质点回到原点;
当共移动次,满足质点回到原点的概率为.
所以共移动N次,满足质点回到原点的概率为.
17.(1)证明见解析
(2)
(3)
【分析】(1)取中点,连接,,借助中位线的性质与平行四边形性质定理可得,结合线面平行判定定理即可得证;
(2)建立适当空间直角坐标系,计算两平面的空间向量,再利用空间向量夹角公式计算即可得解;
(3)借助空间中点到平面的距离公式计算即可得解.
【详解】(1)取中点,连接,,
由是的中点,故,且,
由是的中点,故,且,
则有、,
故四边形是平行四边形,故,
又平面,平面,
故平面;
(2)以为原点建立如图所示空间直角坐标系,
有、、、、、,
则有、、,
设平面与平面的法向量分别为、,
则有,,
分别取,则有、、,,
即、,
则,
故平面与平面的夹角余弦值为;
(3)由,平面的法向量为,
则有,
即点到平面的距离为.
18.(1)学生的性别与是否喜欢运动有关
(2)
【分析】(1)计算卡方,与临界值比较即可得解;
(2)由古典概型概率计算公式结合组合数计算即可得解.
【详解】(1)零假设为:学生的性别与是否喜欢运动无关,
根据列联表中的数据,计算得到,
根据的独立性检验,我们推断不成立,即学生的性别与是否喜欢运动有关.
(2)由题意得选取的喜欢运动的男学生人数为,则不喜欢运动的男学生、喜欢运动的女学生、不喜欢运动的女学生的人数之和为,
则至少有1名喜欢运动的男学生被选中的概率为.
19.(1)
(2)证明见解析
【分析】(1)建立空间直角坐标系,设,根据求出的范围,将平面与平面所成锐二面角的余弦值表示为的函数,再求范围.
(2)是四面体的表面积,可证, ,从而证得结论.
【详解】(1)由题意知,
而,是的中点,所以,
又平面平面,平面平面,平面,
所以平面,
在平面内作的垂直作为轴,所以轴,
如图以E为坐标原点,分别以分别为轴正半轴建立空间直角坐标系:
因为,设,
所以,,,,,
则 ,,
所以,,
,,.
设平面的法向量,
由得,取,
,解得.
设平面的法向量,
由得,取,
设平面与平面所成锐二面角为,则
,
所以平面与平面所成锐二面角余弦值的取值范围是.
(2)是四面体的表面积,,令与面所成角为,
,
,
因为是公垂线,上的点和上的点的最短距离是,
(取不到等号,)
,
,
.
【点睛】关键点点睛:的证明关键是利用公垂线的性质由得到,从而根据建立不等式证明结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年高二数学下学期苏教版2019期末模拟测试卷
考试范围:选择性必修第二册
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知随机变量,若,则( )
A.0.2 B.0.3 C.0.7 D.0.8
2.如图,在正三棱柱中,,P为的中点,则( )
A. B.1 C. D.
3.已知一系列样本点的一个经验回归方程为,若样本点的残差为1,则( )
A. B.6 C. D.8
4.已知空间向量,则向量在向量上的投影向量是( )
A. B. C. D.
5.已知,随机变量的分布列为
4 6 8
设,则( )
A.数列单调递增 B.数列单调递减
C.数列先增后减 D.数列先减后增
6.对四组数据进行统计,获得如图散点图,关于其相关系数的比较,正确的是( )
A. B.
C. D.
7.如图所示是一个以为直径,点为圆心的半圆,其半径为4,为线段的中点,其中,,是半圆圆周上的三个点,且把半圆的圆周分成了弧长相等的四段,若将该半圆围成一个以为顶点的圆锥的侧面,则在该圆锥中下列结果正确的是( )
A.为正三角形 B.平面
C.平面 D.点到平面的距离为
8.已知正方体,设其棱长为1(单位:).平面与正方体的每条棱所成的角均相等,记为.平面与正方体表面相交形成的多边形记为,下列结论正确的是( )
A.可能为三角形,四边形或六边形
B.
C.的面积的最大值为
D.正方体内可以放下直径为的圆
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.的展开式中,下列结论正确的是( )
A.展开式共7项 B.含项的系数为480
C.无常数项 D.所有项的二项式系数之和为128
10.下列说法正确的是( )
A.若回归方程为,则变量x与y负相关
B.运用最小二乘法求得的经验回归直线方程一定经过样本点的中心
C.若散点图中所有点都在直线上,则相关系数
D.若决定系数的值越接近于1,表示回归模型的拟合效果越好
11.如图,平面,,,,,,,则( )
A.
B.平面
C.平面与平面的夹角的余弦值为
D.直线与平面所成角的正弦值为
三、填空题:本题共3小题,每小题5分,共15分.
12.五种活动,甲、乙都要选择三个活动参加.甲选到的概率为 ;已知乙选了活动,他再选择活动的概率为 .
13.设,若,且,则 .
14.如图,在长方体中,已知,.动点P从出发,在棱上匀速运动;动点Q同时从B出发,在棱BC上匀速运动,P的运动速度是Q的两倍,各自运动到另一端点停止.它们在运动过程中,设直线PQ与平面ABCD所成的角为,则的取值范围是 .
四、解答题:本题共5小题,第15小题13分,第16、17小题15分,第18、19小题17分,共77分.解答应写出文字说明、证明过程或演算步骤.
15.现有4名男生和3名女生,
(1)若安排7名学生站成一排照相,要求甲乙排在一起,这样的排法有多少种?
(2)若安排7名学生站成一排照相,要求3名女生互不相邻,这样的排法有多少种?
(3)若邀请7名学生中的4名参加一项活动,其中男生甲和女生乙不能同时参加,求邀请的方法种数.
16.一个质点在随机外力的作用下,从平面直角坐标系的原点出发,每隔1秒等可能地向上 向下 向左或向右移动一个单位.
(1)共移动两次,求质点与原点距离的分布列和数学期望;
(2)分别求移动4次和移动6次质点回到原点的概率;
(3)若共移动次(大于0,且为偶数),求证:质点回到原点的概率为.
17.已知四棱柱中,底面为梯形,,平面,,其中.是的中点,是的中点.
(1)求证平面;
(2)求平面与平面的夹角余弦值;
(3)求点到平面的距离.
18.为了研究学生的性别与是否喜欢运动的关联性,随机调查了某中学的100名学生,整理得到如下列联表:
男学生 女学生 合计
喜欢运动 40 20 60
不喜欢运动 20 20 40
合计 60 40 100
(1)依据的独立性检验,能否认为学生的性别与是否喜欢运动有关联?
(2)按学生的性别以及是否喜欢运动用分层随机抽样的方法从这100名学生中选取10人,再从这10人中任选2人,求至少有1名喜欢运动的男学生被选中的概率.
附:,其中.
0.1 0.05 0.01
2.706 3.841 6.635
19.如图1,在梯形中,,是线段上的一点,,,将沿翻折到的位置.
(1)如图2,若二面角为直二面角,,分别是,的中点,若直线与平面所成角为,,求平面与平面所成锐二面角的余弦值的取值范围;
(2)我们把和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线,点为线段的中点,,分别在线段,上(不包含端点),且为,的公垂线,如图3所示,记四面体的内切球半径为,证明:.
参考答案:
1.D
【分析】利用正态分布的对称性求概率.
【详解】随机变量,,
则,
故.
故选:D.
2.A
【分析】以为基底表示后可求的值.
【详解】由正三棱柱可得,,
而,
故
,
故选:A.
3.C
【分析】观测值减去预测值称为残差;进而利用残差的定义即可求解.
【详解】样本点的观测值为,预测值为,
则残差为,解得.
故选:C.
4.A
【分析】根据向量投影的概念,结合向量的数量积计算得出结果.
【详解】根据题意,, ,,
在上的投影向量可为
故选:A.
5.A
【分析】先由公式求出,得到,由函数性质得到的单调性.
【详解】,,
当,时,数列单调递增.
故选:A.
6.B
【分析】根据散点图和相关系数的概念和性质辨析即可.
【详解】由散点图可知,相关系数所在散点图呈负相关,所在散点图呈正相关,所以都为正数,都为负数.
所在散点图近似一条直线上,线性相关性比较强,相关系数的绝对值越接近,
而所在散点图比较分散,线性相关性比较弱点,相关系数的绝对值越远离.
综上所得:.
故答案为:B.
7.C
【分析】根据题意,还原圆锥原图,找出对应线段长度关系,位置关系.很容易得解.
【详解】选项A,该半圆围成的圆锥,如图所示,
设圆锥底面半径为,则,∴,∴,
∵为的中点,为的中点,∴,且,
∴,为等腰直角三角形,选项A错误;
选项B,若平面,则,直角中,,
∴,选项B错误;
选项C,∵,∴平面,选项C正确;
选项D,∵,,∴平面,∴平面平面,
∴到直线的距离即为到平面的距离,
又∵,∴到直线的距离等于到直线的距离,为,选项D错误;
故选:C.
8.D
【分析】A选项,如图,建立以A为原点的空间直角坐标系,利用向量知识可知平面可为与垂直的平面,即可判断选项正误;B选项,由A选项分析及线面角计算公式可判断选项正误;C选项,由A选项分析可表示出两种情况下的面积表达式,即可判断选项正误;D选项,问题等价于判断内部最大圆直径最大值是否大于1.2.
【详解】A选项,如图,以A为原点建立空间直角坐标系,
则,
.
设平面法向量为,因平面与正方体的每条棱所成的角均相等,
则
.
由对称性,不妨取,则法向量可为,又,
则平面可为与垂直的平面.
如图,连接,
因平面ABCD,平面ABCD,
则,又平面,
则平面,又平面,则,同理可得.
又平面,,故平面.
即平面可为与平面平行的平面,
当平面与(不含A)相交时,M为与相似的正三角形;
当平面与(不含)相交时,M为如图所示的六边形;
当平面与相交时(不含),M为与相似的正三角形;
则可能为三角形,六边形,故A错误;
B选项,由A选项分析可知,,故B错误.
C选项,由A选项分析可知,当平面过或时,
所得正三角形面积最大,由题可得边长为,则相应面积为.
当为六边形时,如下图所示,因,,又,
结合图形可知,又由题可知六边形为中心对称图形,
取其对称中心为O,则四边形四边形四边形,
则六边形面积为相应四边形面积的3倍.取RS,RT中点分别为F,E,
连接EF,OE,OF,因,则,
四边形面积为四边形面积2倍,则六边形面积为四边形面积6倍.
设,
由题结合图形可知, ,则
在中,由余弦定理,.
注意到,则四点共圆,
则外接圆直径等于OR,由正弦定理,可得.
则,.
则六边形面积S
,当且仅当时取等号.
又 ,则的面积的最大值为,故C错误;
D选项,先判断M内部的最大圆直径最大值是否超过1.2m.
当M为正三角形时,M内部的最大圆为三角形内切圆,
易知当平面过或时,所得内切圆半径最大,
设此时内切圆半径为,三角形面积为,周长为C,
则内切圆直径.
当M为六边形时,M内部的最大圆半径满足,
由C选项分析,可知,则当时,
取最大值,则此时M内部的最大圆直径的最大值为,
因,则,即正方体内可以放下直径为的圆,故D正确.
故选:D
【点睛】关键点睛:本题首先需要通过向量方法,得到满足题意的平面的具体特征,后利用几何知识,结合正余弦定理可得图形的面积最大值及其内部最大圆直径.
9.CD
【分析】根据题意,结合二项展开式的性质,以及展开式的通项公式和二项式系数的性质,逐项判定,即可求解.
【详解】对于A中,由二项式的展开式共有8项,所以A错误;
对于B中,由二项式,可得展开式的通项为,
令,可得,则展开式的项的系数为,所以B错误;
对于C中,由,令,可得,
所以展开式中没有常数项,所以C正确;
对于D中,由展开式的二项式系数的性质,可得展开式中所有二项式系数和为,所以D正确.
故选:CD.
10.ABD
【分析】利用正负相关的意义判断A;利用回归直线的性质判断B;利用相关系数、决定系数意义判断CD.
【详解】对于A,回归方程为的斜率为负,则变量x与y负相关,A正确;
对于B,回归直线方程一定经过样本点的中心,B正确;
对于C,散点图中所有点都在直线上,则相关系数,C错误;
对于D,决定系数的值越接近于1,表示回归模型的拟合效果越好,D正确.
故选:ABD
11.BC
【分析】建立空间直角坐标系,利用空间向量法一一计算可得.
【详解】因为平面,,
由题意,以为坐标原点,分别以,,的方向为轴、轴、轴正方向建立空间直角坐标系,
可得,,,,,,
则,,
所以,所以,不垂直,故A错误;
依题意,是平面的法向量,
又,可得,则,
又因为直线平面,所以平面,故B正确;
设为平面的一个法向量,则,
即,令,可得,
依题意,,,
设为平面的法向量,
则,即,不妨令,可得,
所以,
故平面与平面的夹角的余弦值为,故C正确;
设直线与平面所成角为,,
则,故D错误.
故选:BC.
12.
【分析】结合列举法或组合公式和概率公式可求甲选到的概率;采用列举法或者条件概率公式可求乙选了活动,他再选择活动的概率.
【详解】解法一:列举法
从五个活动中选三个的情况有:
,共10种情况,
其中甲选到有6种可能性:,
则甲选到得概率为:;
乙选活动有6种可能性:,
其中再选则有3种可能性:,
故乙选了活动,他再选择活动的概率为.
解法二:
设甲、乙选到为事件,乙选到为事件,
则甲选到的概率为;
乙选了活动,他再选择活动的概率为
故答案为:;
13.56
【分析】分析可知是二项式系数最大的唯一一项,由二项式系数的性质可得,即可得结果.
【详解】因为,
可知,
若,且,则是二项式系数最大的唯一一项,则,
所以.
故答案为:56.
14.
【分析】根据给定条件,建立空间直角坐标系,设,并求出的坐标,再结合线面角的向量求法求解.
【详解】在长方体中,以点为原点,建立如图所示的空间直角坐标系,
设,由P的运动速度是的2倍,得,即,
则,显然平面的法向量,
于是,
,因此,
显然当时,,当时,,
所以的取值范围是.
故答案为:
【点睛】关键点点睛:用向量法求直线与平面所成的角,求出平面的法向量是关键,并注意公式求出的是线面角的正弦.
15.(1)1440
(2)1440
(3)25
【分析】(1)利用捆绑法,结合排列组合知识求解;
(2)利用插空法,结合排列组合知识求解;
(3)利用间接法求解.
【详解】(1)由题意可知:运用捆绑法,可得共有排法数为种.
(2)由题意可知:运用插空法,可得共有排法数为种.
(3)由题意可知:邀请这7名学生中的4名参加一项活动共有种方法,
男生甲和女生乙同时参加的方法有,共有邀请方法数为种.
16.(1)答案见解析;
(2)
(3)证明见解析
【分析】(1)首先求出X的所有可能取值以及对应的概率,再结合离散型随机变量的期望公式求答案即可.
(2)利用分步乘法计数原理、组合以及古典概型的概率公式计算可求得结果.
(3)利用数学归纳法证明即可.
【详解】(1)设表示2次移动中质点与原点距离,则可取0,2,,
当质点向左移动1次向右移动1次,或向上移动1次向下移动1次,最后,则;
当质点向左移动2次或向右移动2次,或向上移动2次或向下移动2次,最后,则;
当质点向左移动1次向上移动1次,或向左移动1次向下移动1次,或向右移动1次向上移动1次,或向右移动1次向下移动1次,最后,则
的分布列为:
0
.
(2)质点从原点出发,每次等可能地向上 向下 向左或向右移动一个单位,共移动4次,
可能的结果共有种情况,
若质点回到原点,则向左移动2次向右移动2次,或向上移动2次向下移动2次,共有种情况,
若质点回到原点,则向左移动1次向右移动1次,向上移动1次向下移动1次,共有种情况,
所以质点回到原点的概率为.
质点从原点出发,每次等可能地向上 向下 向左或向右移动一个单位,共移动6次,
可能的结果共有种情况,
若质点回到原点,则向左移动3次向右移动3次,或向上移动3次向下移动3次,共有种情况,
若质点回到原点,则向左移动2次向右移动2次,向上移动1次向下移动1次,则向左移动1次向右移动1次,向上移动2次向下移动2次,共有种情况,
所以质点回到原点的概率为.
(3)若共移动2次,质点回到原点的概率为;
假设共移动N次,满足质点回到原点的概率为;
当共移动次,
移动N次质点回到原点当质点向左移动1次向右移动1次,或向上移动1次向下移动1次,移动次质点回到原点;
移动N次质点在,当质点向左移动2次或向右移动2次,或向上移动2次或向下移动2次,移动次质点回到原点;
移动N次质点在当质点向左移动1次向上移动1次,或向左移动1次向下移动1次,或向右移动1次向上移动1次,或向右移动1次向下移动1次,,移动N+2次质点回到原点;
当共移动次,满足质点回到原点的概率为.
所以共移动N次,满足质点回到原点的概率为.
17.(1)证明见解析
(2)
(3)
【分析】(1)取中点,连接,,借助中位线的性质与平行四边形性质定理可得,结合线面平行判定定理即可得证;
(2)建立适当空间直角坐标系,计算两平面的空间向量,再利用空间向量夹角公式计算即可得解;
(3)借助空间中点到平面的距离公式计算即可得解.
【详解】(1)取中点,连接,,
由是的中点,故,且,
由是的中点,故,且,
则有、,
故四边形是平行四边形,故,
又平面,平面,
故平面;
(2)以为原点建立如图所示空间直角坐标系,
有、、、、、,
则有、、,
设平面与平面的法向量分别为、,
则有,,
分别取,则有、、,,
即、,
则,
故平面与平面的夹角余弦值为;
(3)由,平面的法向量为,
则有,
即点到平面的距离为.
18.(1)学生的性别与是否喜欢运动有关
(2)
【分析】(1)计算卡方,与临界值比较即可得解;
(2)由古典概型概率计算公式结合组合数计算即可得解.
【详解】(1)零假设为:学生的性别与是否喜欢运动无关,
根据列联表中的数据,计算得到,
根据的独立性检验,我们推断不成立,即学生的性别与是否喜欢运动有关.
(2)由题意得选取的喜欢运动的男学生人数为,则不喜欢运动的男学生、喜欢运动的女学生、不喜欢运动的女学生的人数之和为,
则至少有1名喜欢运动的男学生被选中的概率为.
19.(1)
(2)证明见解析
【分析】(1)建立空间直角坐标系,设,根据求出的范围,将平面与平面所成锐二面角的余弦值表示为的函数,再求范围.
(2)是四面体的表面积,可证, ,从而证得结论.
【详解】(1)由题意知,
而,是的中点,所以,
又平面平面,平面平面,平面,
所以平面,
在平面内作的垂直作为轴,所以轴,
如图以E为坐标原点,分别以分别为轴正半轴建立空间直角坐标系:
因为,设,
所以,,,,,
则 ,,
所以,,
,,.
设平面的法向量,
由得,取,
,解得.
设平面的法向量,
由得,取,
设平面与平面所成锐二面角为,则
,
所以平面与平面所成锐二面角余弦值的取值范围是.
(2)是四面体的表面积,,令与面所成角为,
,
,
因为是公垂线,上的点和上的点的最短距离是,
(取不到等号,)
,
,
.
【点睛】关键点点睛:的证明关键是利用公垂线的性质由得到,从而根据建立不等式证明结论.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
