数学高中人教A版必修一2.3 幂函数课件(15张)
文档属性
| 名称 | 数学高中人教A版必修一2.3 幂函数课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 932.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-20 22:10:44 | ||
图片预览






文档简介
课件15张PPT。§2.3 幂函数人教A版 必修一 高一数学学习目标 知识与技能
理解并掌握幂函数的图象与性质,能初步运用所学知识
解决有关问题,培养灵活思维能力.
过程与方法
通过具体函数归纳与概括幂函数定义、图象和性质,体
验数学概念的形成过程,培养学生的抽象概括能力.
情感、态度与价值观
培养学生数形结合、分类讨论的思想,以及分析归纳的
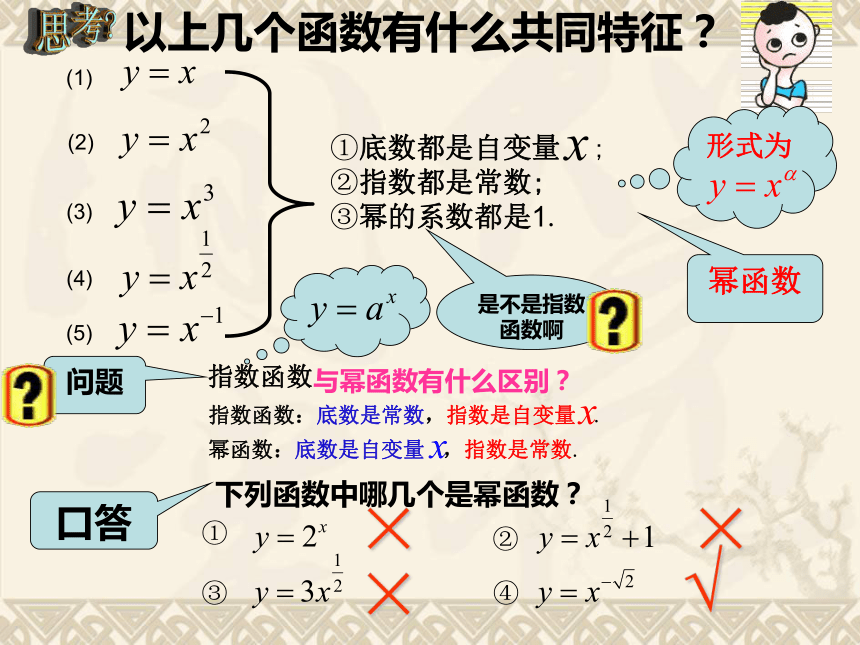
能力,培养学生合作交流的意识. 学习重点 从具体函数归纳认识幂函数的一些性质并简单应用. 学习难点 概括幂函数的性质. 问题1:如果张红购买了每千克1元的水果w千克,那么她需要付的钱数p= 元,问 题 情 境这里p是w的函数 这里S是a的函数 这里V是a的函数 这里a是S的函数 这里 是t的函数 aaSVSa问题2:如果正方形的边长为a,那么正方形的面积S= ,问题3:如果正方体的边长为a,那么正方体的体积V= ,问题4:如果正方形场地面积为S,那么正方形的边长a= ,问题5:如果某人ts内骑车行进了1km,那么他骑车的速度 = km/s.若将它们的自变量用 来表示,函数值用 来表示,则它们的函数关系式将是:以上几个函数有什么共同特征?幂函数是不是指数函数啊指数函数口答下列函数中哪几个是幂函数?① ②③④×××√形式为问题与幂函数有什么区别?①底数都是自变量 ;
②指数都是常数;
③幂的系数都是1.指数函数:底数是常数,指数是自变量 .幂函数:底数是自变量 ,指数是常数.一、幂函数定义练一练几点说明:1、对于幂函数,我们只讨论 =1,2,3, ,-1时的情形.解:2、幂函数的定义方式是一种形式定义,解析式是幂的形式,
底数是自变量 ,指数是常数,幂的系数为1.1、证明幂函数 是奇函数.证明:为奇函数.性 质 证 明
(1,1)二、五个常用幂函数的图象:(2,4)(-2,4)(-1,-1)X 0 1 2 3 4 …0 0.71 1 1.41 1.73 2 …X … -1 0 1 …… -3.38 -1 -0.13 0 0.13 1 3.38 …观察图象,将你发现的结论填在下表中RRRRR奇函数偶函数非奇非偶奇函数奇函数 R上
增函数 R上
增函数(1,1) ∪∪增减减减增幂函数性质知识小结(1)函数
在(0,+∞)上都有定义,
并且图象都过点(1,1).(2)函数
是奇函数; 是偶函数.(3)在第一象限内, 是增函数;
是减函数.(4)在第一象限内, 图象向上与 轴无限
接近;向右与 轴无限接近.证明:,则分子有理化≤性 质 证 明比较下列各组数值大小: 例<><>比较幂值的大小时利用相应函数单调性,
若指数相同转化为幂函数,
底数相同时转化为指数函数. 解:2、比较下列数值大小 :4、设 ,则使函数 定义域为R
且为奇函数的所有 值为( ) .(A) 1,3 (B)-1,1 (C) -1,3 (D) -1,1,3< 自变量 , 是常数.2、五种常见幂函数的图象及其性质.你的收获?课后习题 2.3 1、2、3.作业谢 谢 大 家!
理解并掌握幂函数的图象与性质,能初步运用所学知识
解决有关问题,培养灵活思维能力.
过程与方法
通过具体函数归纳与概括幂函数定义、图象和性质,体
验数学概念的形成过程,培养学生的抽象概括能力.
情感、态度与价值观
培养学生数形结合、分类讨论的思想,以及分析归纳的
能力,培养学生合作交流的意识. 学习重点 从具体函数归纳认识幂函数的一些性质并简单应用. 学习难点 概括幂函数的性质. 问题1:如果张红购买了每千克1元的水果w千克,那么她需要付的钱数p= 元,问 题 情 境这里p是w的函数 这里S是a的函数 这里V是a的函数 这里a是S的函数 这里 是t的函数 aaSVSa问题2:如果正方形的边长为a,那么正方形的面积S= ,问题3:如果正方体的边长为a,那么正方体的体积V= ,问题4:如果正方形场地面积为S,那么正方形的边长a= ,问题5:如果某人ts内骑车行进了1km,那么他骑车的速度 = km/s.若将它们的自变量用 来表示,函数值用 来表示,则它们的函数关系式将是:以上几个函数有什么共同特征?幂函数是不是指数函数啊指数函数口答下列函数中哪几个是幂函数?① ②③④×××√形式为问题与幂函数有什么区别?①底数都是自变量 ;
②指数都是常数;
③幂的系数都是1.指数函数:底数是常数,指数是自变量 .幂函数:底数是自变量 ,指数是常数.一、幂函数定义练一练几点说明:1、对于幂函数,我们只讨论 =1,2,3, ,-1时的情形.解:2、幂函数的定义方式是一种形式定义,解析式是幂的形式,
底数是自变量 ,指数是常数,幂的系数为1.1、证明幂函数 是奇函数.证明:为奇函数.性 质 证 明
(1,1)二、五个常用幂函数的图象:(2,4)(-2,4)(-1,-1)X 0 1 2 3 4 …0 0.71 1 1.41 1.73 2 …X … -1 0 1 …… -3.38 -1 -0.13 0 0.13 1 3.38 …观察图象,将你发现的结论填在下表中RRRRR奇函数偶函数非奇非偶奇函数奇函数 R上
增函数 R上
增函数(1,1) ∪∪增减减减增幂函数性质知识小结(1)函数
在(0,+∞)上都有定义,
并且图象都过点(1,1).(2)函数
是奇函数; 是偶函数.(3)在第一象限内, 是增函数;
是减函数.(4)在第一象限内, 图象向上与 轴无限
接近;向右与 轴无限接近.证明:,则分子有理化≤性 质 证 明比较下列各组数值大小: 例<><>比较幂值的大小时利用相应函数单调性,
若指数相同转化为幂函数,
底数相同时转化为指数函数. 解:2、比较下列数值大小 :4、设 ,则使函数 定义域为R
且为奇函数的所有 值为( ) .(A) 1,3 (B)-1,1 (C) -1,3 (D) -1,1,3<
