数学人教A版(2019)必修第一册5.1.2弧度制 课件(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册5.1.2弧度制 课件(共21张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-29 22:48:50 | ||
图片预览






文档简介
(共21张PPT)
5.1.2 弧度制
一、情境导学 提出问题
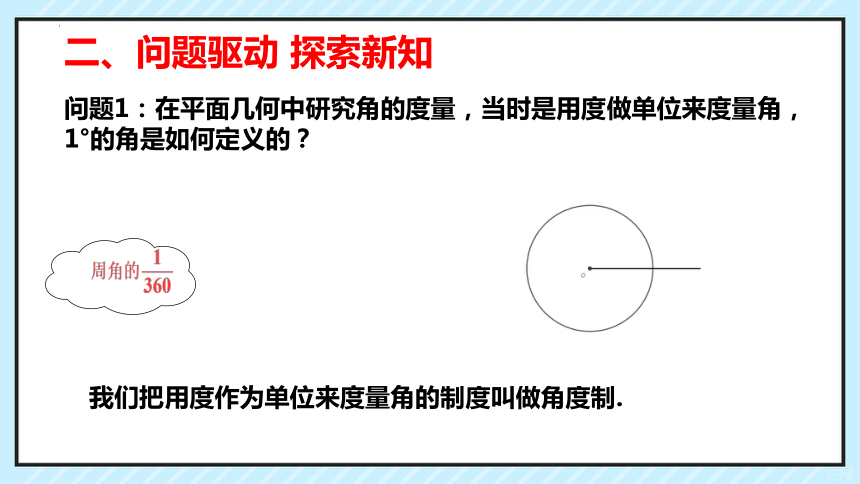
问题1:在平面几何中研究角的度量,当时是用度做单位来度量角,
1°的角是如何定义的?
我们把用度作为单位来度量角的制度叫做角度制.
二、问题驱动 探索新知
问题2:扇子打开过程中可以抽象成什么图形?
圆心角、半径、弧长中哪些没有变化?哪些变化?怎样变化?
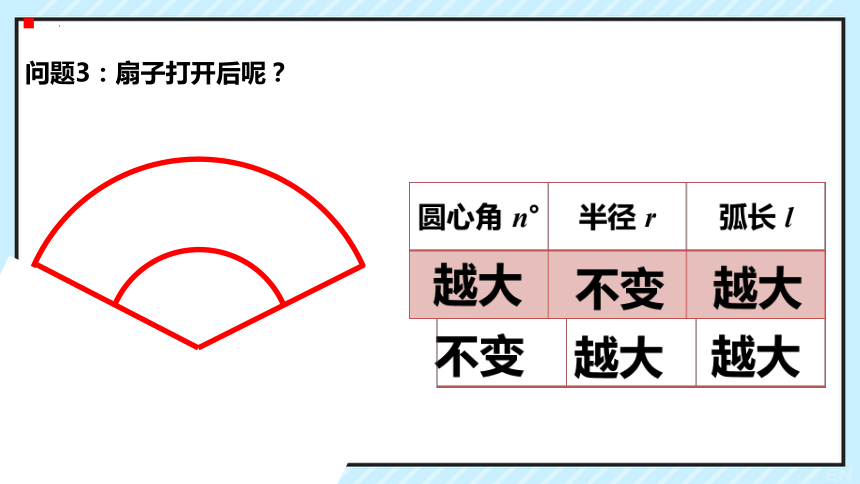
问题3:扇子打开后呢?
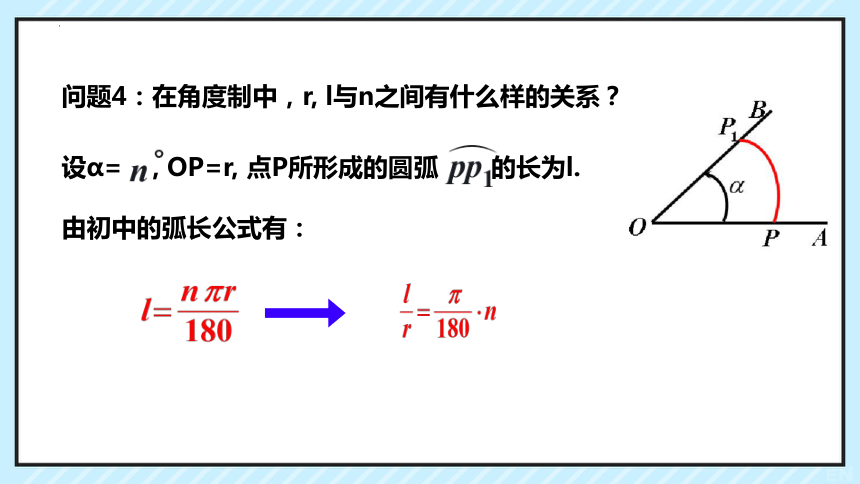
问题4:在角度制中,r, l与n之间有什么样的关系?
设α= , OP=r, 点P所形成的圆弧 的长为l.
由初中的弧长公式有:
长度等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角,单位用符号rad表示,读作弧度。
O
l=r
1rad
三、归纳总结,建构概念
这种用“弧度”做单位来度量角的制度叫做弧度制.
1748年欧拉在他的著作《无穷小分析概论》中明确提出弧度制思想,即以半径为单位来量弧长,统一了角和长度的单位。
数学教师汤姆生首先使用了“弧度”一词,将“半径” (radius) 的前四个字母与“角”(angle)的前两个字母合在一起,构成radian,并被人们广泛接受和引用.
问题5:如果半径分别为 的圆,圆心角α 所对的弧长为 ,那么角α 的弧度数如何计算?
四、灵活转化,完善认知
问题6(1)一个圆周角以度为单位度量是 ,
以弧度为单位度量是 弧度.
(2)由此可得度和弧度有怎样的换算关系?
(3)根据上述关系1°= rad; 1 rad=
即
例1. (1)把 、 化成弧度
(2)把 化成角度
写出一些特殊角对应的角度和弧度.
正角
负角
零角
正实数
负实数
0
四、灵活转化,完善认知
角
角度制
弧度制
单位规定
换算关系
度量单位
度(60进制)
弧度(10进制)
长度等于半径的弧所对的圆心角叫做1弧度
说明:用弧度表示角时,常常把弧度数写成多少 的形式,不必写成小数.
小结:
问题7: 若己知圆心角的弧度数 α 与半径 ,如何求扇形面积
已知扇形的圆心角为120°,半径为 cm,则此扇形的面积为______cm2.
五、回归情境,解决问题
已知扇形的周长为 10cm, 面积为 4cm2, 求扇形圆心角的弧度数.
能力提升
六、总结归纳,提炼概念
本节课你有哪些体会和收获?
作业:分层练习(三十九)
七、课后检测 拓展延伸
七、课后检测,拓展延伸
一、基础过关
1、一条弦的长等于半径,这条弦所对的圆心角等于1弧度么?为什么?
2、把下列角度化成弧度
(1)-150° (2)1095° (3)1440°
3、把下列弧度化成角度
(1) (2)
能力提升
4、已知一扇形的圆心角为 ,半径为 ,弧长为 .若扇形的周长为20cm, 当扇形的圆心角 为多少弧度时,这个扇形的面积最大?
5.1.2 弧度制
一、情境导学 提出问题
问题1:在平面几何中研究角的度量,当时是用度做单位来度量角,
1°的角是如何定义的?
我们把用度作为单位来度量角的制度叫做角度制.
二、问题驱动 探索新知
问题2:扇子打开过程中可以抽象成什么图形?
圆心角、半径、弧长中哪些没有变化?哪些变化?怎样变化?
问题3:扇子打开后呢?
问题4:在角度制中,r, l与n之间有什么样的关系?
设α= , OP=r, 点P所形成的圆弧 的长为l.
由初中的弧长公式有:
长度等于半径长的圆弧所对的圆心角叫做1弧度(radian)的角,单位用符号rad表示,读作弧度。
O
l=r
1rad
三、归纳总结,建构概念
这种用“弧度”做单位来度量角的制度叫做弧度制.
1748年欧拉在他的著作《无穷小分析概论》中明确提出弧度制思想,即以半径为单位来量弧长,统一了角和长度的单位。
数学教师汤姆生首先使用了“弧度”一词,将“半径” (radius) 的前四个字母与“角”(angle)的前两个字母合在一起,构成radian,并被人们广泛接受和引用.
问题5:如果半径分别为 的圆,圆心角α 所对的弧长为 ,那么角α 的弧度数如何计算?
四、灵活转化,完善认知
问题6(1)一个圆周角以度为单位度量是 ,
以弧度为单位度量是 弧度.
(2)由此可得度和弧度有怎样的换算关系?
(3)根据上述关系1°= rad; 1 rad=
即
例1. (1)把 、 化成弧度
(2)把 化成角度
写出一些特殊角对应的角度和弧度.
正角
负角
零角
正实数
负实数
0
四、灵活转化,完善认知
角
角度制
弧度制
单位规定
换算关系
度量单位
度(60进制)
弧度(10进制)
长度等于半径的弧所对的圆心角叫做1弧度
说明:用弧度表示角时,常常把弧度数写成多少 的形式,不必写成小数.
小结:
问题7: 若己知圆心角的弧度数 α 与半径 ,如何求扇形面积
已知扇形的圆心角为120°,半径为 cm,则此扇形的面积为______cm2.
五、回归情境,解决问题
已知扇形的周长为 10cm, 面积为 4cm2, 求扇形圆心角的弧度数.
能力提升
六、总结归纳,提炼概念
本节课你有哪些体会和收获?
作业:分层练习(三十九)
七、课后检测 拓展延伸
七、课后检测,拓展延伸
一、基础过关
1、一条弦的长等于半径,这条弦所对的圆心角等于1弧度么?为什么?
2、把下列角度化成弧度
(1)-150° (2)1095° (3)1440°
3、把下列弧度化成角度
(1) (2)
能力提升
4、已知一扇形的圆心角为 ,半径为 ,弧长为 .若扇形的周长为20cm, 当扇形的圆心角 为多少弧度时,这个扇形的面积最大?
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
