人教版六年级下册数学鸽巢问题课件(共21张PPT)
文档属性
| 名称 | 人教版六年级下册数学鸽巢问题课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-29 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
义务教育人教版六年级下册
第 2 课时
鸽巢问题(2)
第5单元
数学广角—鸽巢问题
学习目标:
1.理解反比例的意义,能正确判断两种量是不是成反比例关系。
2.经历反比例意义的探究过程,培养观察比较、分析、概括的能力。
3.通过一系列富有探究性的问题,进一步渗透自主学习和他人合作交流的意识,激发学习热情。
探究新知
盒子里有同样大小的红球和蓝球各4个,要想摸
出的球一定有2个同色的,至少要摸出几个球?
3
从题中你获取了哪些信息?
同桌间相互说一说,引导学生着重理解“至少”的含义。
你们能猜测出结果吗?
至少要摸出2个球。
至少要摸出5个球。
至少要摸出3个球。
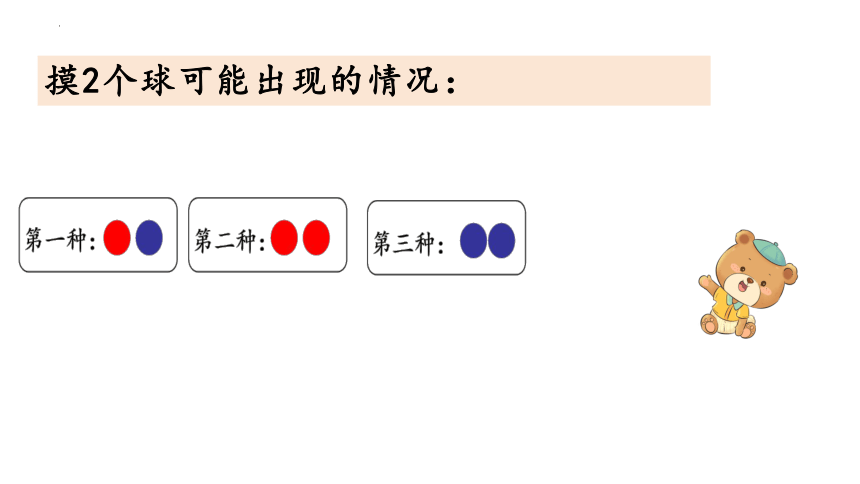
摸2个球可能出现的情况:
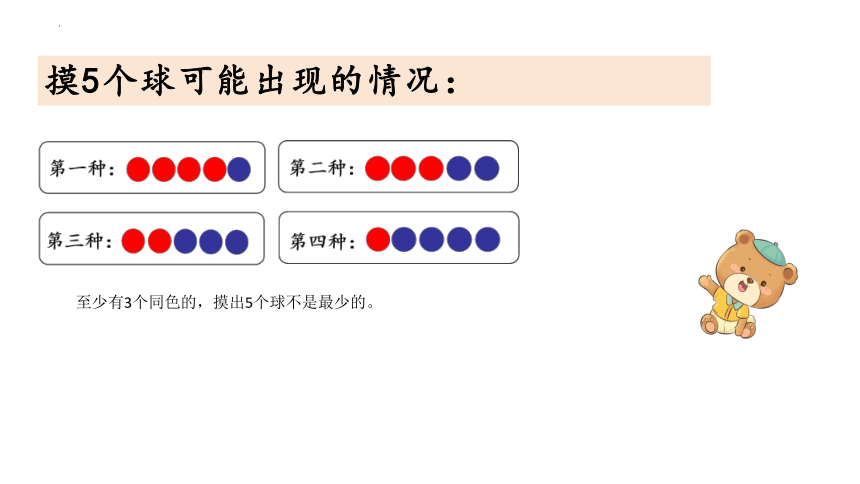
摸5个球可能出现的情况:
至少有3个同色的,摸出5个球不是最少的。
摸3个球可能出现的情况:
至少有3个同色的,摸出5个球不是最少的。
通过验证,你们得到了什么结论?
要想摸出的球一定有2个同色的,至少要摸出3个球。
回顾解题过程,联系前面学习的知识,这是一个什么问题?
上面的问题是“抽屉原理”,颜色数就是抽屉数。
现在你能用例1的知识来解答这一题吗?
只要摸出的球数比它们的颜色种数多1,就能保证至少有2个球同色。
盒子里有同样大小的红、黄、蓝球各6个,要想摸出的球一定有2个同色的球,至少要摸出几个球?
(1)说一说“抽屉”是什么?“抽屉”有几个?
(2)说一说解题思路。
巩固提升
一、填空。
1.一副扑克牌共54张,其中1~13点各有4种,还有两张王牌,至少要取出( )张才能保证其中必有4张牌的点数相同。
2.某小学有1千多名学生,从学生中最少选取( )人,才能使得这些人中有两人属相相同。
3.某校六年级有3个班,在一次数学竞赛中,至少有( )人获奖才能保证获奖的同学中一定有4名学生同班。
巩固提升
1.一副扑克牌共54张,其中1~13点各有4种,还有两张王牌,至少要取出( 42 )张才能保证其中必有4张牌的点数相同。
2.某小学有1千多名学生,从学生中最少选取( 13 )人,才能使得这些人中有两人属相相同。
3.某校六年级有3个班,在一次数学竞赛中,至少有( 10 )人获奖才能保证获奖的同学中一定有4名学生同班。
巩固提升
二、判断。
1.六年级共有370名学生,一定有两人的生日是同一天。 ( )
2.把5块糖分给3个小朋友,有两种分法。 ( )
3.某班有49名学生,班级中一定有5人是同一个月出生 。( )
巩固提升
二、判断。
1.六年级共有370名学生,一定有两人的生日是同一天。 ( √ )
2.把5块糖分给3个小朋友,有两种分法。 ( × )
3.某班有49名学生,班级中一定有5人是同一个月出生 。( √ )
板书设计
鸽巢问题(2)
抽屉数——颜色数
只要摸出的球数比它们的颜色种数多1,就能保证至少有2个球同色。
这节课你收获到了什么?
课后总结
义务教育人教版六年级下册
第 2 课时
鸽巢问题(2)
第5单元
数学广角—鸽巢问题
学习目标:
1.理解反比例的意义,能正确判断两种量是不是成反比例关系。
2.经历反比例意义的探究过程,培养观察比较、分析、概括的能力。
3.通过一系列富有探究性的问题,进一步渗透自主学习和他人合作交流的意识,激发学习热情。
探究新知
盒子里有同样大小的红球和蓝球各4个,要想摸
出的球一定有2个同色的,至少要摸出几个球?
3
从题中你获取了哪些信息?
同桌间相互说一说,引导学生着重理解“至少”的含义。
你们能猜测出结果吗?
至少要摸出2个球。
至少要摸出5个球。
至少要摸出3个球。
摸2个球可能出现的情况:
摸5个球可能出现的情况:
至少有3个同色的,摸出5个球不是最少的。
摸3个球可能出现的情况:
至少有3个同色的,摸出5个球不是最少的。
通过验证,你们得到了什么结论?
要想摸出的球一定有2个同色的,至少要摸出3个球。
回顾解题过程,联系前面学习的知识,这是一个什么问题?
上面的问题是“抽屉原理”,颜色数就是抽屉数。
现在你能用例1的知识来解答这一题吗?
只要摸出的球数比它们的颜色种数多1,就能保证至少有2个球同色。
盒子里有同样大小的红、黄、蓝球各6个,要想摸出的球一定有2个同色的球,至少要摸出几个球?
(1)说一说“抽屉”是什么?“抽屉”有几个?
(2)说一说解题思路。
巩固提升
一、填空。
1.一副扑克牌共54张,其中1~13点各有4种,还有两张王牌,至少要取出( )张才能保证其中必有4张牌的点数相同。
2.某小学有1千多名学生,从学生中最少选取( )人,才能使得这些人中有两人属相相同。
3.某校六年级有3个班,在一次数学竞赛中,至少有( )人获奖才能保证获奖的同学中一定有4名学生同班。
巩固提升
1.一副扑克牌共54张,其中1~13点各有4种,还有两张王牌,至少要取出( 42 )张才能保证其中必有4张牌的点数相同。
2.某小学有1千多名学生,从学生中最少选取( 13 )人,才能使得这些人中有两人属相相同。
3.某校六年级有3个班,在一次数学竞赛中,至少有( 10 )人获奖才能保证获奖的同学中一定有4名学生同班。
巩固提升
二、判断。
1.六年级共有370名学生,一定有两人的生日是同一天。 ( )
2.把5块糖分给3个小朋友,有两种分法。 ( )
3.某班有49名学生,班级中一定有5人是同一个月出生 。( )
巩固提升
二、判断。
1.六年级共有370名学生,一定有两人的生日是同一天。 ( √ )
2.把5块糖分给3个小朋友,有两种分法。 ( × )
3.某班有49名学生,班级中一定有5人是同一个月出生 。( √ )
板书设计
鸽巢问题(2)
抽屉数——颜色数
只要摸出的球数比它们的颜色种数多1,就能保证至少有2个球同色。
这节课你收获到了什么?
课后总结
