探索勾股定理1

课件23张PPT。没有大胆的猜想，就没有伟大的发现。 ---牛顿成功的奥秘在于多动手。
---杨振宁 探索勾股定理（1）

李 伟
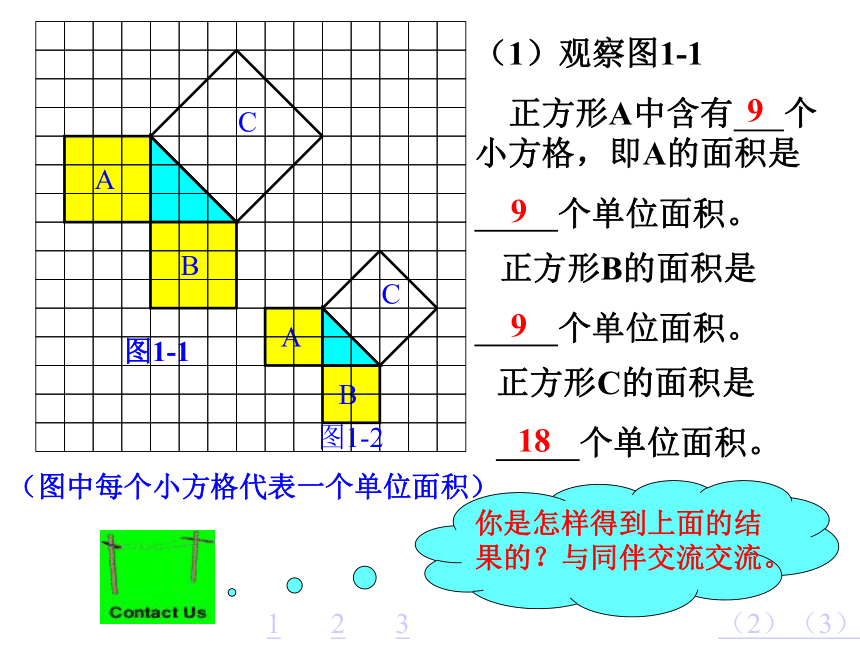
隆德二中（1）观察图1-1
正方形A中含有 个小方格，即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
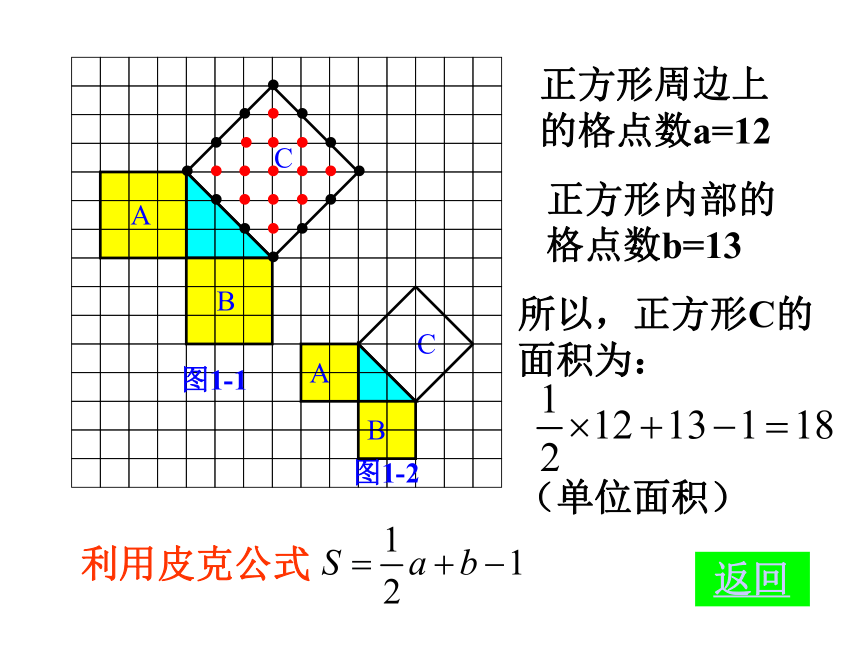
个单位面积。99918123（2）（3）正方形周边上的格点数a=12正方形内部的格点数b=13利用皮克公式所以，正方形C的面积为：

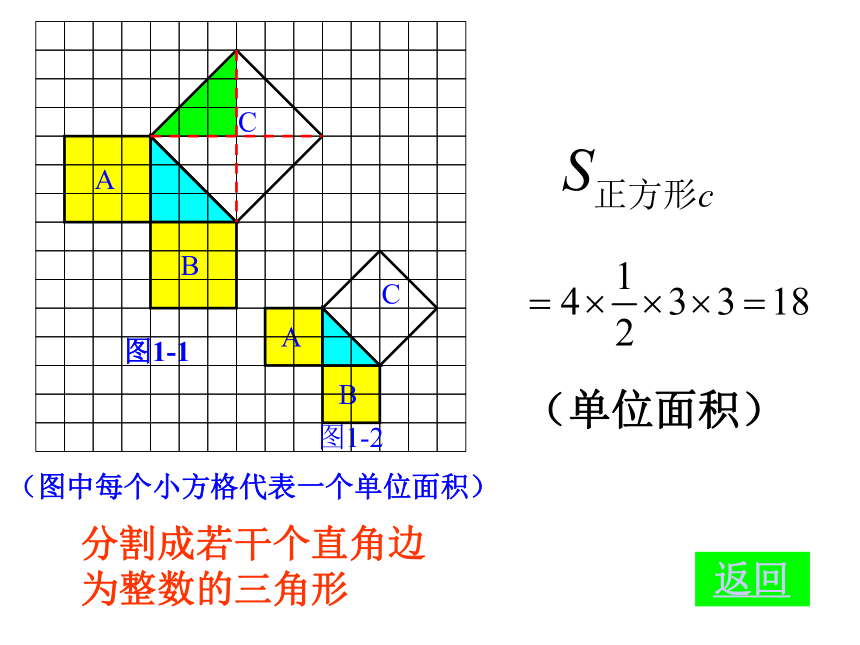
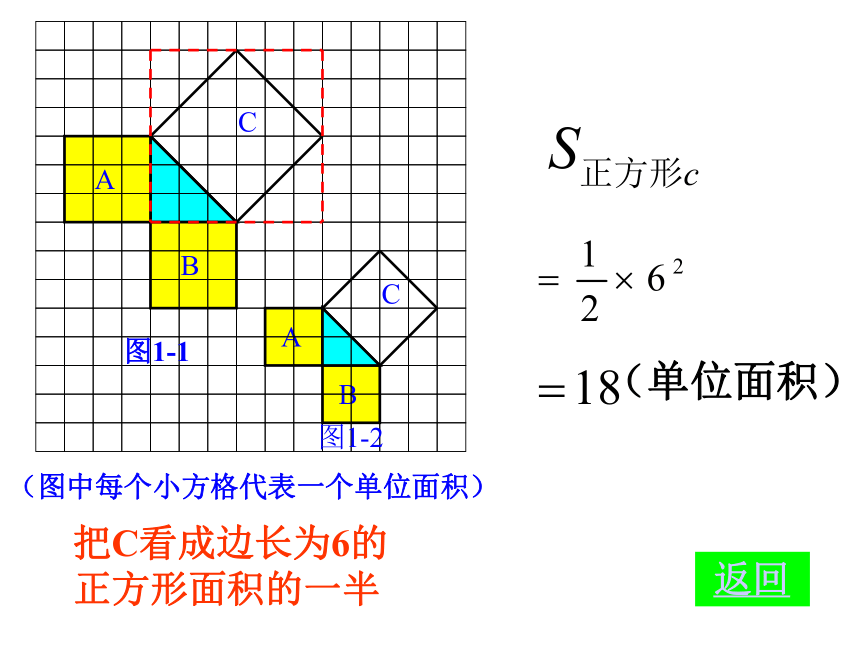
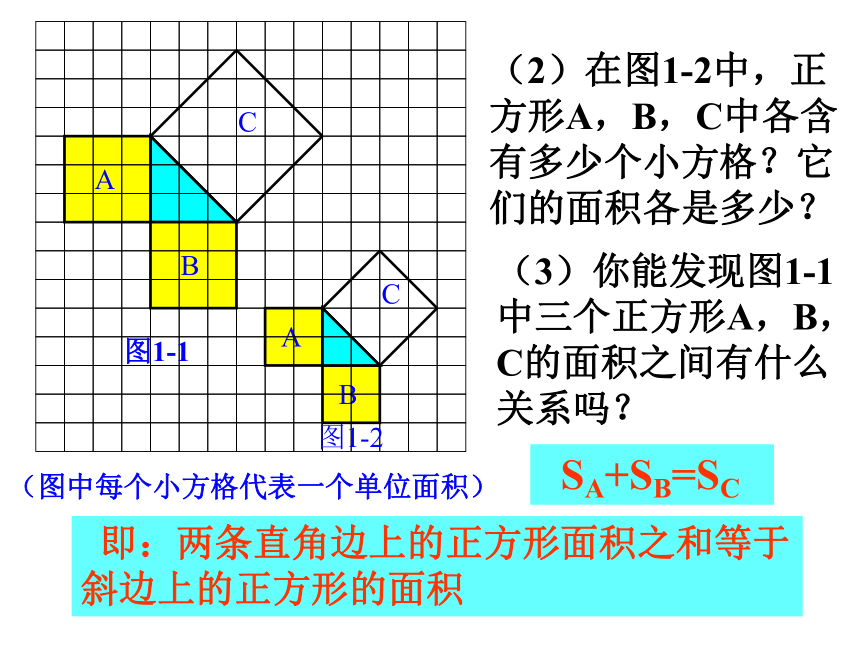
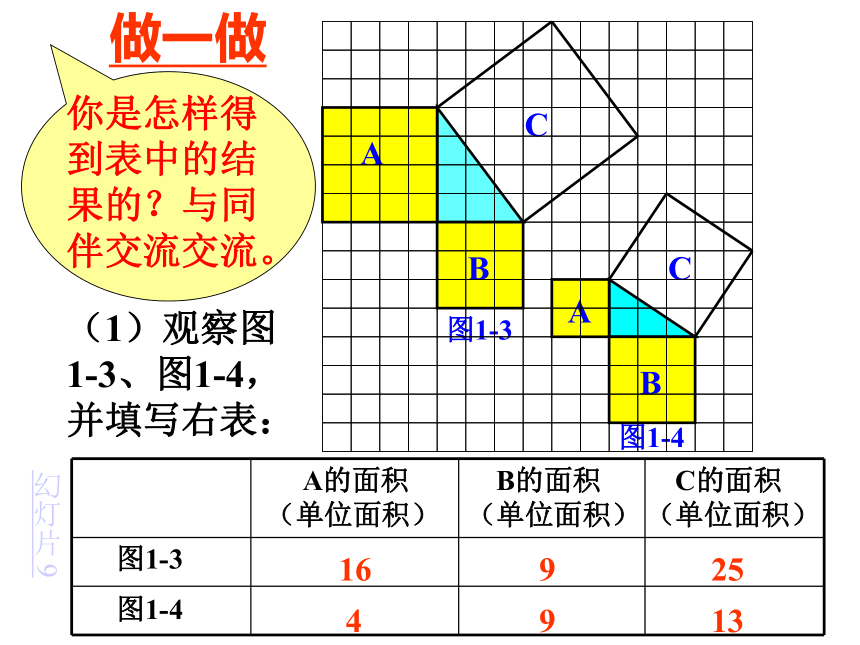
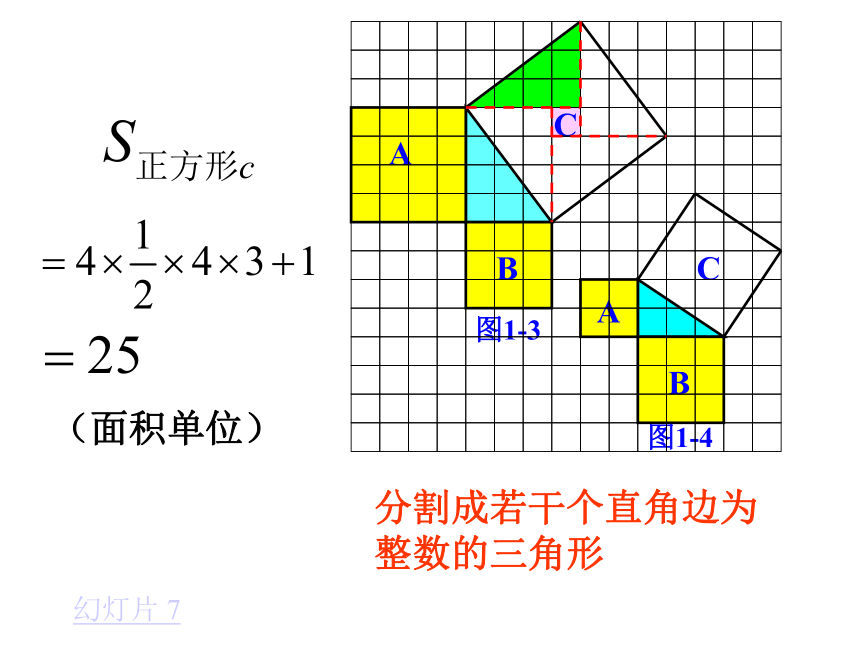
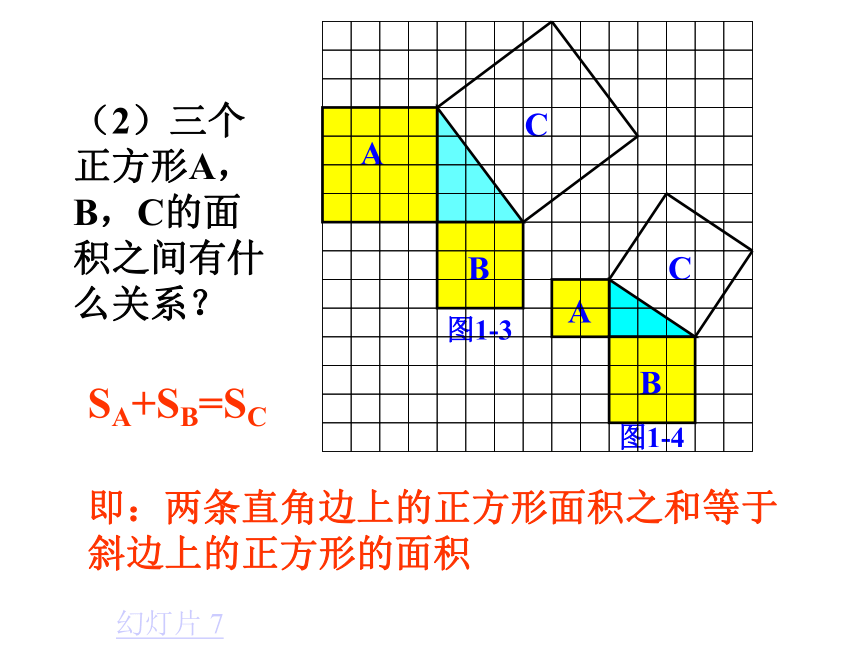
（单位面积） 返回图1-1图1-2分割成若干个直角边为整数的三角形（单位面积） 返回（单位面积）把C看成边长为6的正方形面积的一半 返回（2）在图1-2中，正方形A，B，C中各含有多少个小方格？它们的面积各是多少？（3）你能发现图1-1中三个正方形A，B，C的面积之间有什么关系吗？ SA+SB=SC 即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积（1）观察图1-3、图1-4，并填写右表： A的面积（单位面积） B的面积（单位面积） C的面积（单位面积）图1-3图1-4169254913做一做幻灯片 9分割成若干个直角边为整数的三角形（面积单位）幻灯片 7（2）三个正方形A，B，C的面积之间有什么关系？SA+SB=SC
即：两条直角边上的正方形面积之和等于 斜边上的正方形的面积幻灯片 7议一议：
（1）你能发现直角三角形三边之间存在什么关系吗？abc如果：三角形的边长分别为a、b、c那么：它们有什么关系呢？a2 + b2 = c2面积A面积B面积C=a2=b2=c2面积A+面积B=面积C议一议：你能发现直角三角形三边长度之间存在什么关系吗？两直角边的平方和等于斜边的平方勾股弦读一读 勾股世界
我国是最早了解勾股定理的国家之一。早在三多年前，周朝数学家商高就提出，将一根直尺折成一个直角三角形，如果勾等于三，股等于四，那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处，还记载了勾股定理的一般形式。
1945年，人们在研究古巴比伦人遗留下的一块数学泥板时，惊讶地发现上面竟然刻有15组能构成直角三角形三边的数，其年代远在商高之前。
相传二千多年前，希腊的毕达哥拉斯学派首先证明了勾股定理，因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派，1955年希腊曾经发行了一枚纪念邮票，你能看出邮票上的图案所反映的内容吗？勾股定理的命名
2.西方国家称勾股定理为毕达哥拉斯定理.
毕达哥拉斯(Pythagoras,约公元前580～前500年)是古希
腊杰出的数学家,天文学家,哲学家.他不仅提出了定理,
而且努力探求证明方法.
1.约2000年前,我国古代算书《周髀算经》中就记载了公
元前1120年我国古人发现的“勾三股四弦五”.当时把
较短的直角边叫做勾,较长的边叫做股,斜边叫做弦. “
勾三股四弦五”的意思是,在直角三角形中, 如果勾为3,
股为4,那么弦为5.这里3 +4 = 5 .人们还发现, 勾为6,
股为8, 弦一定为10.勾为5,股为12, 弦一定为13等.同
样,有6 +8 =10 ,5 +12 = 13 ,…,即勾 +股 =弦 .所
以,我国称它为勾股定理.定 理 的 历 史 及 证 明★ 公元前11世纪，周公与商高的对话（记录于公元前1世纪《周髀算经》）中提出“勾三、股四、弦五”。——勾股定理、商高定理★ 《周髀算经》中还记载了公元前六、七世纪的荣方与陈子的对话，再次提到勾股定理。——陈子定理★ 公元前600年左右，古希腊的毕达哥拉斯学派发现勾股定理，命名为“毕达哥拉斯定理” （百牛定理），而且给出了证明。★ 古巴比仑人在公元前19世纪也发现此定理。★ 中国最早给出定理证明的是公元3世纪三国时吴国数学家赵爽（赵君卿）。★ 定理从提出到现在的两千多年中，已经找到证明400多种，由鲁密斯搜集整理的《毕达哥拉斯》一书中就给出370种不同证法。练一练：1、求下列字母所代表的正方形的面积。解：正方形A的面积
=225+400
=625 解：正方形B的面积
=81+225
=306 2、求出下列直角三角形中未知边的长度：∵x＞0
∴x = 53、下列阴影部分是一个正方形，求此正方形的面积解：设正方形的边长为x厘米 , 则 x2=172-152
x2=64答：正方形的面积是64平方厘米。1.在Rt△ABC中， ∠A， ∠B， ∠C　的对边为a，b，c.(1)已知a=6，b=8，则c= ;(2)已知c=25，b=15，则a = ;(3)已知a:b=3:4，c=15，则 b = ;巩固性练习2. 一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少? ABC3、如图，一根旗杆在离地面9米处断裂，旗杆顶部落在离旗杆底部12米处，旗杆折断之前有多高？作业：
P6的3、4题及没做完的补充练习题
上网查有关勾股定理的历史资料