探索勾股定理2

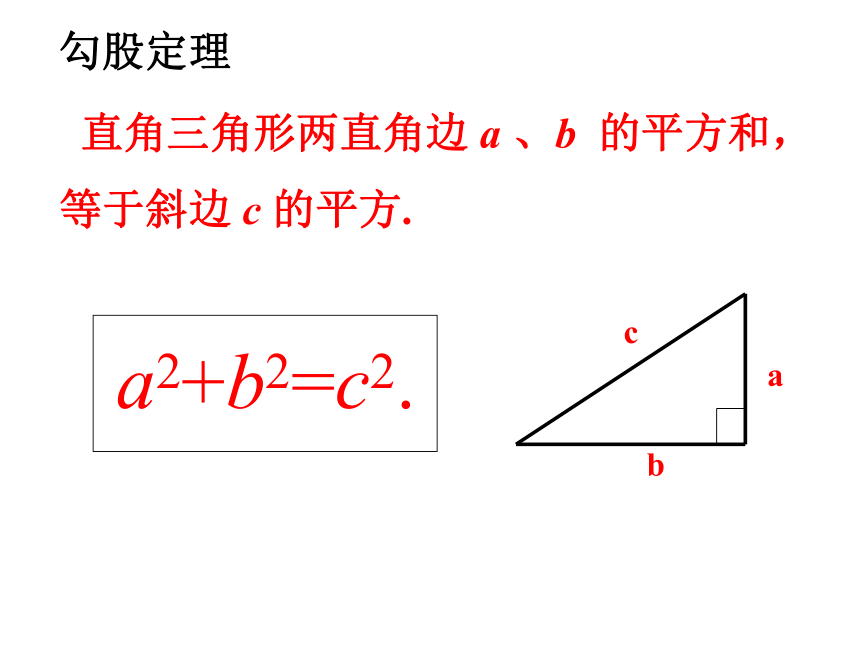
课件19张PPT。探索勾股定理（2）隆德二中 李伟你知道直角三角形的三边长
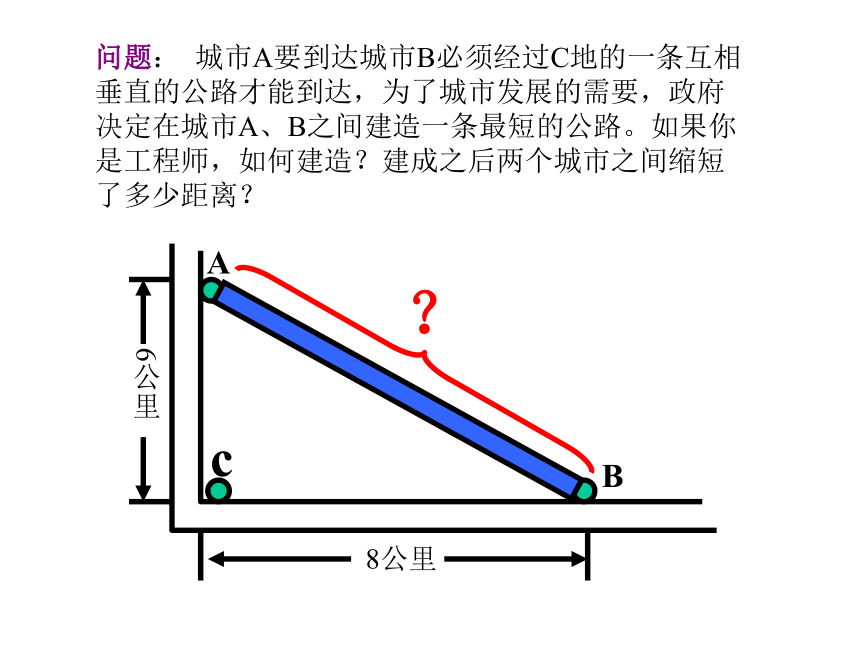
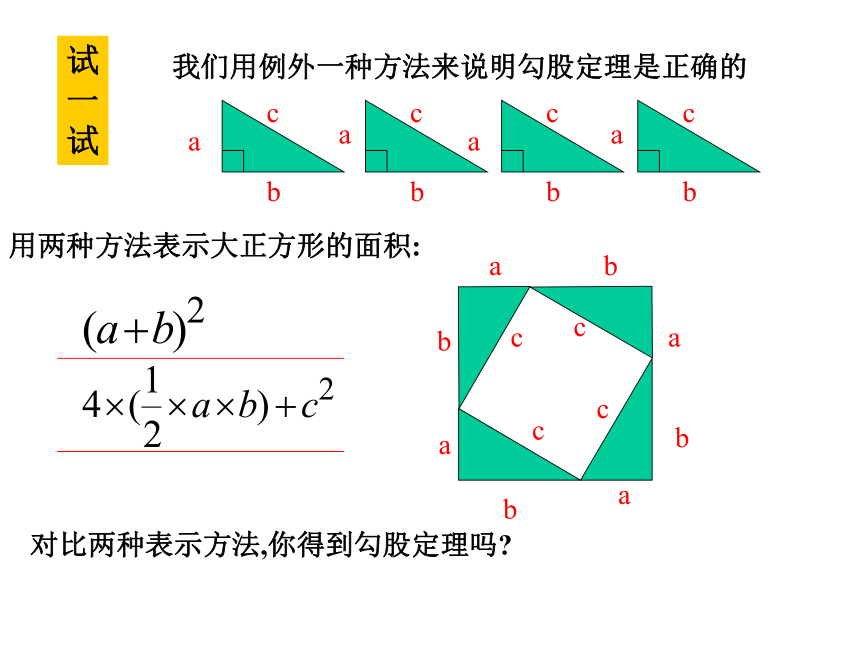
有什么关系吗?a b c ?复习勾股定理AB问题： 城市A要到达城市B必须经过C地的一条互相垂直的公路才能到达，为了城市发展的需要，政府决定在城市A、B之间建造一条最短的公路。如果你是工程师，如何建造？建成之后两个城市之间缩短了多少距离？8公里6公里c利用拼图来验证勾股定理：1、准备四个全等的直角三角形（设直角三角形的两条直角边分别为a，b，斜边为c）；2、你能用这四个直角三角形拼成一个正方形吗？拼一拼试试看3、你拼的正方形中是否含有以斜边c的正方形？4、你能否就你拼出的图说明a2+b2=c2？用两种方法表示大正方形的面积:对比两种表示方法,你得到勾股定理吗?试
一
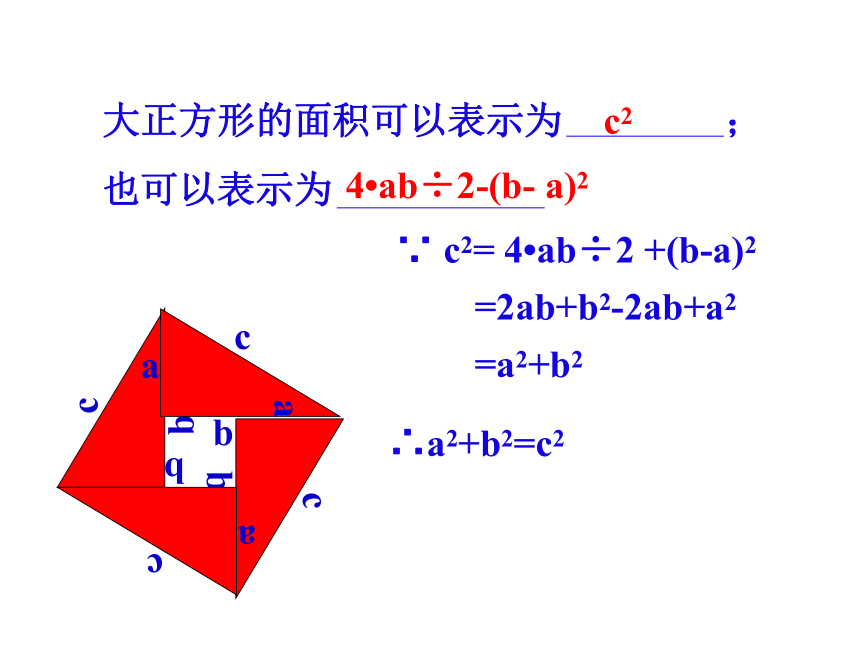
试我们用例外一种方法来说明勾股定理是正确的∵ c2= 4?ab÷2 +(b-a)2 =2ab+b2-2ab+a2 =a2+b2∴a2+b2=c2大正方形的面积可以表示为 ；
也可以表示为c24?ab÷2-(b- a)2
实践出真知飞机在天空中水平飞行,某一时刻刚好飞到一个男孩头顶正上方
4000米处,过了20秒,飞机距离这个男孩头顶5000米,飞机每时飞行
多少千米?
20秒4000米5000米 在1876年一个周末的傍晚，在美国首都华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景……他走着走着，突然发现附近的一个小石凳上，有两个小孩正在聚精会神地谈论着什么，时而大声争论，时而小声探讨．由于好奇心驱使他循声向两个小孩走去，想搞清楚两个小孩到底在干什么．只见一个小男孩正俯着身子用树枝在地上画着一个直角三角形……
趣闻调查组报告“总统”证法勾股定理的 于是这位中年人不再散步，立即回家，潜心探讨小男孩给他留下的难题。他经过反复的思考与演算，终于弄清楚了其中的道理，并给出了简洁的证明方法。????? 1876年4月1日，他在《新英格兰教育日志》上发表了他对勾股定理的这一证法。???? 1881年，这位中年人—伽菲尔德就任美国第二十任总统。后来，人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明，就把这一证法称为“总统”证法。 美国总统证法：补充练习：
1、放学以后，小红和小颖从学校分手，分别沿着东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖用20分钟到家，小红和小颖家的距离为 （ ）
A、600米； B、800米； C、1000米； D、不能确定
2、直角三角形两直角边分别为5厘米、12厘米，那么斜边上的高是 （ ）
A、6厘米； B、 8厘米； C、 80/13厘米；D、 60/13厘米；
CD3、甲、乙两位探险者到沙漠进行探险.某日早晨8:00
甲先出发,他以6千米/小时的速度向东行走,1时
后乙出发,他以5千米/小时的速度向北行进,上午
10:00,甲、乙二人相距多远?东北甲乙4、等腰三角形底边上的高为8，周长为32，求这个三角形的面积8DABC解：设这个三角形为ABC，高为AD，设AB为X，则BC为（32-2X），BD是（16－x) 由勾股定理得：
X2=(16-X)2 +82即X2=256-32X+X2 +64∴ X=10∴ S?ABC=BC?AD/2=2 ?6 ?8/2=485.如图在△ABC中，∠ACB=90o， CD⊥AB，D为垂足，AC=2.1cm,BC=2.8cm.
求① △ABC的面积；
②斜边AB的长；
③斜边AB上的高CD的长。一渔翁在湖中钓鱼，忽然一陈狂风吹来，把湖中的一朵荷花吹倒并沉落水中，渔翁说荷花的茎长五尺，沉入湖中的残花离根部三尺，问我们湖深多少尺？ 提高性练习请思考：如图，分别以直角三角形三边为直径作三个半圆
这三个半圆的面积之间有什么关系？为什么？议一议： 观察下图，判断图中三角形的三边是否满足 a2 + b2 = c2再见