2023-2024学年山东省青岛市莱西四中七年级(下)质检数学试卷(五四学制)(含答案)
文档属性
| 名称 | 2023-2024学年山东省青岛市莱西四中七年级(下)质检数学试卷(五四学制)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 186.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-29 00:00:00 | ||
图片预览



文档简介
2023-2024学年山东省青岛市莱西四中七年级(下)质检数学试卷(五四学制)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”请用数学知识解释图中这一现象,其原因是( )
A. 两点之间,线段最短
B. 过一点有无数条直线
C. 两点确定一条直线
D. 两点之间线段的长度,叫做这两点之间的距离
2.计算的结果是( )
A. B. C. D.
3.计算的结果是( )
A. B. C. D.
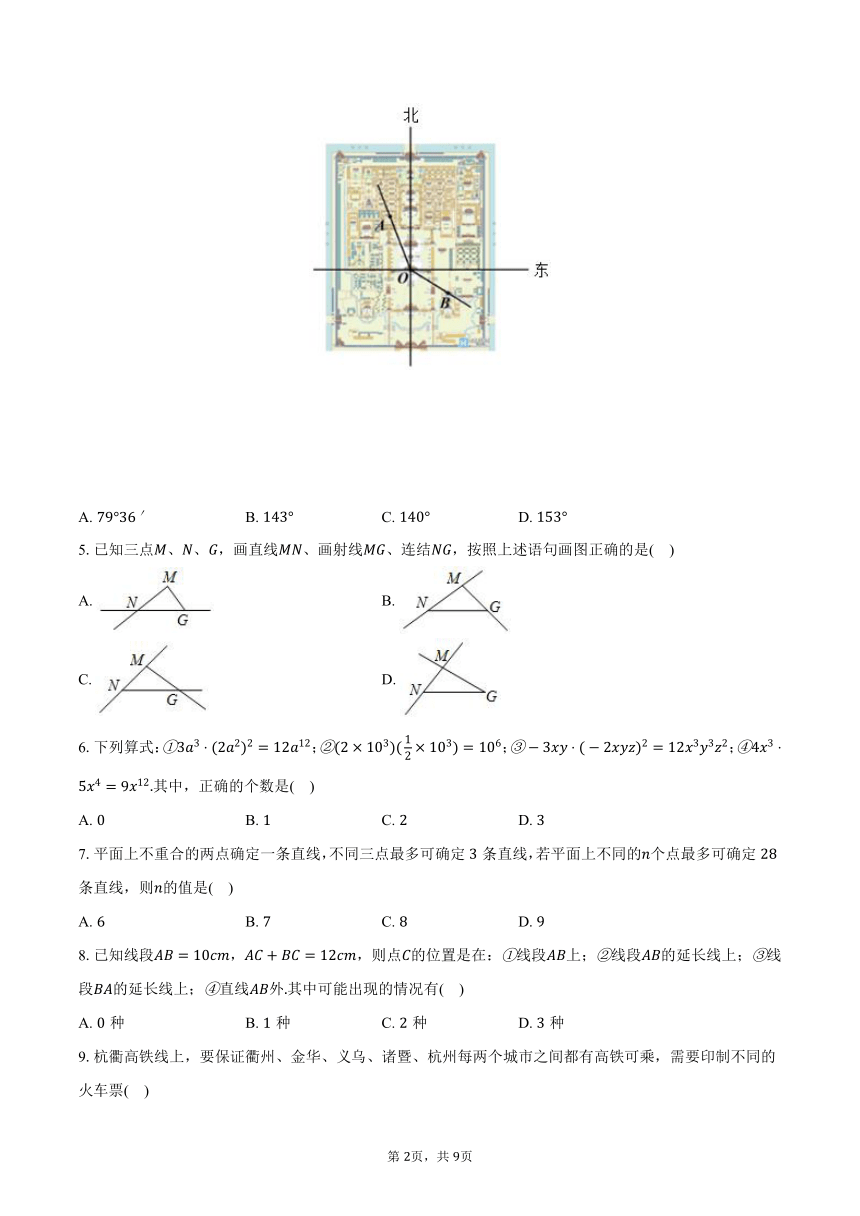
4.中国古代大建筑群平面中统率全局的轴线称为“中轴线”,北京中轴线是古代中国独特城市规划理论的产物,故宫是北京中轴线的重要组成部分.故宫中也有一条中轴线,北起神武门经乾清宫、保和殿、太和殿、南到午门,这条中轴线同时也在北京城的中轴线上.图中是故宫博物院的主要建筑分布图.其中,点表示养心殿所在位置,点表示太和殿所在位置,点表示文渊阁所在位置.已知养心殿位于太和殿北偏西方向上,文渊阁位于太和殿南偏东方向上,则的度数是( )
A. B. C. D.
5.已知三点、、,画直线、画射线、连结,按照上述语句画图正确的是( )
A. B.
C. D.
6.下列算式:;;;其中,正确的个数是( )
A. B. C. D.
7.平面上不重合的两点确定一条直线,不同三点最多可确定条直线,若平面上不同的个点最多可确定条直线,则的值是( )
A. B. C. D.
8.已知线段,,则点的位置是在:线段上;线段的延长线上;线段的延长线上;直线外其中可能出现的情况有( )
A. 种 B. 种 C. 种 D. 种
9.杭衢高铁线上,要保证衢州、金华、义乌、诸暨、杭州每两个城市之间都有高铁可乘,需要印制不同的火车票( )
A. 种 B. 种 C. 种 D. 种
10.如图,、是线段上两点,、分别是线段,的中点,下列结论:
若,则;,则;;其中正确的结论是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.钟表上的时间是时分,此时时针与分针所成的夹角是______度
12.已知点是线段的三等分点,是的中点,,则线段长______.
13.如图,平分,平分若,,则______度.
14.若,则 ______.
15.若,则______.
16.计算: ______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:
;
.
18.本小题分
用简便方法计算:
.
.
19.本小题分
计算:
;
20.本小题分
如图,已知线段和外一点.
画线段,直线.
用尺规在线段上作出点,使保留作图痕迹
21.本小题分
如图,已知,是的平分线,是的平分线.
求的度数;
若,求的度数.
22.本小题分
如图,线段,点是线段的中点,点是线段的中点.
求线段的长;
若在线段上有一点,,求的长.
23.本小题分
已知,求的值.
已知,求的值.
24.本小题分
阅读下列文字,并解决问题已知,求的值.
分析:考虑到满足的,的可能值较多,则不能逐一代入求解,故考虑整体思想,将整体代入
解:
.
请你用上述方法解决问题:已知,求的值.
25.本小题分
【新知理解】
如图,点在线段上,图中共有三条线段、和,若其中有一条线段的长度是另外一条线段长度的倍,则称点是线段的“巧点”.
线段的中点______这条线段的“巧点”;填“是”或“不是”.
若,点是线段的巧点,则______;
【解决问题】
如图,已知动点从点出发,以的速度沿向点匀速移动:点从点出发,以的速度沿向点匀速移动,点、同时出发,当其中一点到达终点时,运动停止,设移动的时间为当为何值时,、、三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或
13.
14.
15.
16.
17.解:
;
.
18.解:
;
.
19.解:
;
.
20.解:如图,线段,直线即为所求.
如图,线段即为所求作的线段.
21.解:平分,
,
,
,
同理:,
;
解:当在内部时,
,
当在外部时,
,
综上,或.
22.解:,是的中点,
,
是的中点,
,
;
,,
,
当在的左边时,;
当在的右边时,.
的长为或.
23.解:
,
把代入得:原式.
,
,
.
24.解:
.
25.解:是;
或或;
秒后,,,
由题意可知不可能为、两点的巧点,此情况排除.
当为、的巧点时,
Ⅰ,即,解得;
Ⅱ,即,解得;
Ⅲ,即,解得;
当为、的巧点时,
Ⅰ,即,解得舍去;
Ⅱ,即,解得;
Ⅲ,即,解得
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”请用数学知识解释图中这一现象,其原因是( )
A. 两点之间,线段最短
B. 过一点有无数条直线
C. 两点确定一条直线
D. 两点之间线段的长度,叫做这两点之间的距离
2.计算的结果是( )
A. B. C. D.
3.计算的结果是( )
A. B. C. D.
4.中国古代大建筑群平面中统率全局的轴线称为“中轴线”,北京中轴线是古代中国独特城市规划理论的产物,故宫是北京中轴线的重要组成部分.故宫中也有一条中轴线,北起神武门经乾清宫、保和殿、太和殿、南到午门,这条中轴线同时也在北京城的中轴线上.图中是故宫博物院的主要建筑分布图.其中,点表示养心殿所在位置,点表示太和殿所在位置,点表示文渊阁所在位置.已知养心殿位于太和殿北偏西方向上,文渊阁位于太和殿南偏东方向上,则的度数是( )
A. B. C. D.
5.已知三点、、,画直线、画射线、连结,按照上述语句画图正确的是( )
A. B.
C. D.
6.下列算式:;;;其中,正确的个数是( )
A. B. C. D.
7.平面上不重合的两点确定一条直线,不同三点最多可确定条直线,若平面上不同的个点最多可确定条直线,则的值是( )
A. B. C. D.
8.已知线段,,则点的位置是在:线段上;线段的延长线上;线段的延长线上;直线外其中可能出现的情况有( )
A. 种 B. 种 C. 种 D. 种
9.杭衢高铁线上,要保证衢州、金华、义乌、诸暨、杭州每两个城市之间都有高铁可乘,需要印制不同的火车票( )
A. 种 B. 种 C. 种 D. 种
10.如图,、是线段上两点,、分别是线段,的中点,下列结论:
若,则;,则;;其中正确的结论是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.钟表上的时间是时分,此时时针与分针所成的夹角是______度
12.已知点是线段的三等分点,是的中点,,则线段长______.
13.如图,平分,平分若,,则______度.
14.若,则 ______.
15.若,则______.
16.计算: ______.
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:
;
.
18.本小题分
用简便方法计算:
.
.
19.本小题分
计算:
;
20.本小题分
如图,已知线段和外一点.
画线段,直线.
用尺规在线段上作出点,使保留作图痕迹
21.本小题分
如图,已知,是的平分线,是的平分线.
求的度数;
若,求的度数.
22.本小题分
如图,线段,点是线段的中点,点是线段的中点.
求线段的长;
若在线段上有一点,,求的长.
23.本小题分
已知,求的值.
已知,求的值.
24.本小题分
阅读下列文字,并解决问题已知,求的值.
分析:考虑到满足的,的可能值较多,则不能逐一代入求解,故考虑整体思想,将整体代入
解:
.
请你用上述方法解决问题:已知,求的值.
25.本小题分
【新知理解】
如图,点在线段上,图中共有三条线段、和,若其中有一条线段的长度是另外一条线段长度的倍,则称点是线段的“巧点”.
线段的中点______这条线段的“巧点”;填“是”或“不是”.
若,点是线段的巧点,则______;
【解决问题】
如图,已知动点从点出发,以的速度沿向点匀速移动:点从点出发,以的速度沿向点匀速移动,点、同时出发,当其中一点到达终点时,运动停止,设移动的时间为当为何值时,、、三点中其中一点恰好是另外两点为端点的线段的巧点?说明理由
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或
13.
14.
15.
16.
17.解:
;
.
18.解:
;
.
19.解:
;
.
20.解:如图,线段,直线即为所求.
如图,线段即为所求作的线段.
21.解:平分,
,
,
,
同理:,
;
解:当在内部时,
,
当在外部时,
,
综上,或.
22.解:,是的中点,
,
是的中点,
,
;
,,
,
当在的左边时,;
当在的右边时,.
的长为或.
23.解:
,
把代入得:原式.
,
,
.
24.解:
.
25.解:是;
或或;
秒后,,,
由题意可知不可能为、两点的巧点,此情况排除.
当为、的巧点时,
Ⅰ,即,解得;
Ⅱ,即,解得;
Ⅲ,即,解得;
当为、的巧点时,
Ⅰ,即,解得舍去;
Ⅱ,即,解得;
Ⅲ,即,解得
第1页,共1页
同课章节目录
