2024年湖北省中考数学试题(含答案)(非回忆版)
文档属性
| 名称 | 2024年湖北省中考数学试题(含答案)(非回忆版) |  | |
| 格式 | docx | ||
| 文件大小 | 445.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-30 22:05:04 | ||
图片预览




文档简介
2024年湖北省中考数学试卷
一、选择题(共10题,每题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求)
1.在实际生产生活中,经常用正数、负数表示具有相反意义的量,如果把收入20元记作+20元,那么支出10元记作( )
A.+10元 B.﹣10元 C.+20元 D.﹣20元
2.如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
3.计算2x 3x2的结果是( )
A.5x2 B.6x2 C.5x3 D.6x3
4.如图,一条公路的两侧铺设了AB,CD两条平行管道,并有纵向管道AC连通,若∠1=120°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
5.不等式x+1≥2的解集在数轴上表示正确的是( )
A. B.
C. D.
6.在下列事件中,必然事件是( )
A.掷一次骰子,向上一面的点数是3
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.任意画一个三角形,其内角和是180°
7.我国古代数学著作《九章算术》中记载了一个关于“方程”的问题:“今有牛五、羊二,直金十两,牛二、羊五,直金八两.问牛羊各直金几何?”译文:“今有牛5头,羊2头,共值金10两,牛2头,羊5头,共值金8两,问牛、羊每头各值金多少?”若设牛每头值金x两,羊每头值金y两,则可列方程组是( )
A. B.
C. D.
8.如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠ABC的内部相交于点D,画射线BD,连接AC.若∠CAB=50°,则∠CBD的度数是( )
A.30° B.25° C.20° D.15°
9.如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
10.已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)的顶点坐标为(﹣1,﹣2),与y轴的交点在x轴上方,下列结论正确的是( )
A.a<0 B.c<0 C.a﹣b+c=﹣2 D.b2﹣4ac=0
二、填空题(共5题,每题3分,共15分)
11.写出一个大于﹣1的数是 .
12.小亮了解了祖冲之、刘徽、赵爽、杨辉、秦九韶这5位著名数学家的生平简介,知晓他们取得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成就进行分享,选到数学家赵爽的概率是 .
13.铁的密度为7.9g/cm3,铁块的质量m(单位:g)与它的体积V(单位:cm3)之间的函数关系式为m=7.9V,当V=10cm3时,m= g.
14.计算的结果是 .
15.如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 ;(2)DG的长是 .
三、解答题(共9题,共75分、解答应写出文字说明、证明过程或演算步骤)
16.(6分)计算:(﹣1)×322﹣20240.
17.(6分)如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:BE=DF.
18.(6分)某数学兴趣小组在校园内开展综合与实践活动,记录如下:
活动项目 测量校园中树AB的高度
活动方案 “测角仪”方案 “平面镜”方案
方案示意图
实施过程 ①选取与树底B位于同一水平地面的D处; ②测量D,B两点间的距离; ③站在D处,用测角仪测量从眼睛C处看树顶A的仰角∠ACF; ④测量C到地面的高度CD. ①选取与树底B位于同一水平地面的E处; ②测量E,B两点间的距离; ③在E处水平放置一个平面镜,沿射线BE方向后退至D处,眼睛C刚好从镜中看到树顶A; ④测量E,D两点间的距离; ⑤测量C到地面的高度CD.
测量数据 ①DB=10m; ②∠ACF=32.5°; ③CD=1.6m. ①EB=10m; ②ED=2m; ③CD=1.6m.
备注 ①图上所有点均在同一平面内; ②AB,CD均与地面垂直; ③参考数据:tan32.5≈0.64. ①图上所有点均在同一平面内; ②AB,CD均与地面垂直; ③把平面镜看作一个点,并由物理学知识可得∠CED=∠AEB.
请你从以上两种方案中任选一种,计算树AB的高度.
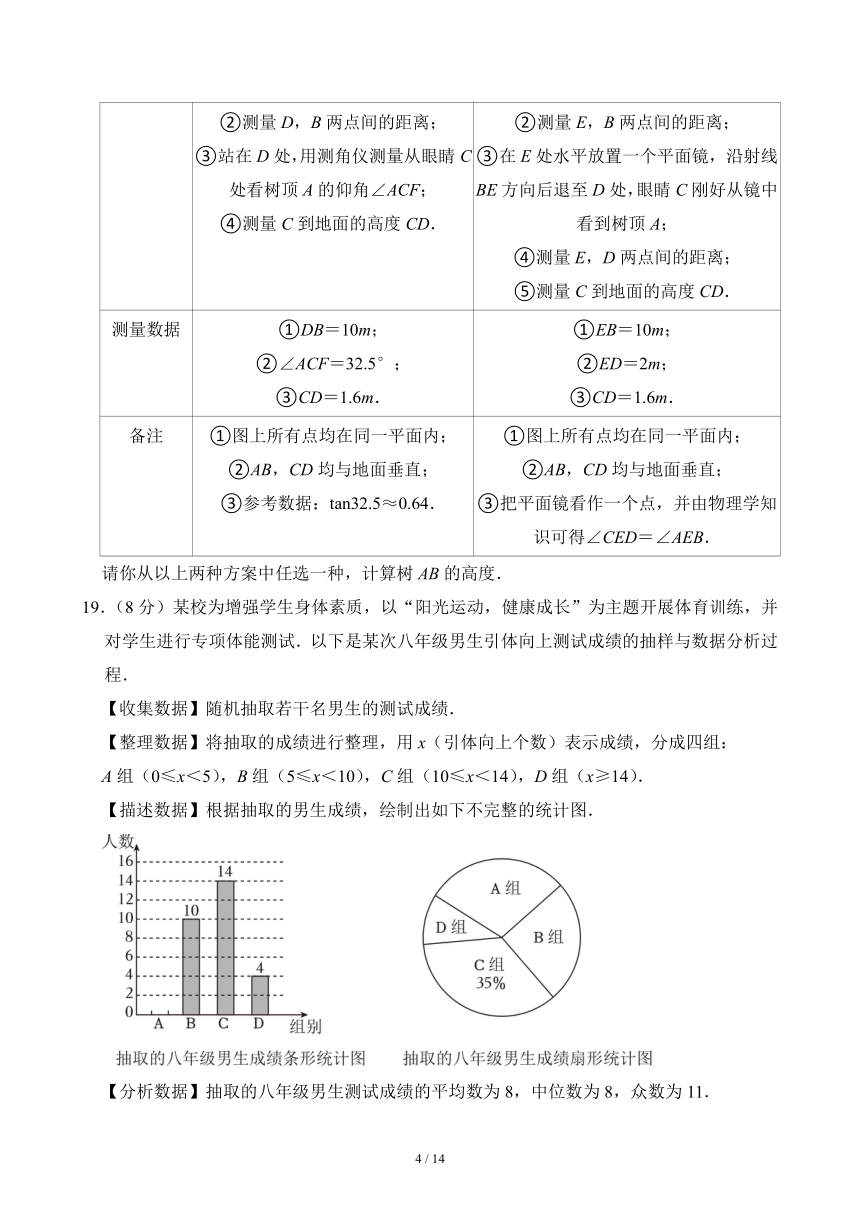
19.(8分)某校为增强学生身体素质,以“阳光运动,健康成长”为主题开展体育训练,并对学生进行专项体能测试.以下是某次八年级男生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用x(引体向上个数)表示成绩,分成四组:
A组(0≤x<5),B组(5≤x<10),C组(10≤x<14),D组(x≥14).
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本题中的意义.
20.(8分)如图,一次函数y=x+m的图象与x轴交于点A(﹣3,0),与反比例函数y(k为常数,k≠0)的图象在第一象限的部分交于点B(n,4).
(1)求m,n,k的值;
(2)若C是反比例函数y的图象在第一象限部分上的点,且△AOC的面积小于△AOB的面积,直接写出点C的横坐标a的取值范围.
21.(8分)如图,在Rt△ABC中,∠ACB=90°,点E在AC上,以CE为直径的⊙O经过AB上的点D,与OB交于点F,且BD=BC.
(1)求证:AB是⊙O的切线;
(2)若AD,AE=1,求的长.
22.(10分)如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m,栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:m2).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到750m2吗?如果能,求x的值;如果不能,请说明理由;
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
23.(11分)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
24.(12分)在平面直角坐标系中,抛物线y=﹣x2+bx+3与x轴交于点A(﹣1,0)和点B,与y轴交于点C.
(1)求b的值;
(2)如图,M是第一象限抛物线上的点,∠MAB=∠ACO,求点M的横坐标;
(3)将此抛物线沿水平方向平移,得到的新抛物线记为L,L与y轴交于点N,设L的顶点横坐标为n,NC的长为d.
①求d关于n的函数解析式;
②L与x轴围成的区域记为U,U与△ABC内部重合的区域(不含边界)记为W,当d随n的增大而增大,且W内恰好有两个横、纵坐标均为整数的点时,直接写出n的取值范围.
2024年湖北省中考数学试题参考答案
一、选择题(共10题,每题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求)
1.B 2.A 3.D 4.B 5.A
6.D 7.A 8.C 9.B 10.C
二、填空题(共5题,每题3分,共15分)
11.0 12. 13.79 14.1 15.
三、解答题(共9题,共75分、解答应写出文字说明、证明过程或演算步骤)
16.(6分)解:原式=﹣3+3+4﹣1=3.
17.(6分)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
18.(6分)解:“测角仪”方案:过C作CF⊥AB于F,
∵CD⊥BD,AB⊥BD,
∴四边形CDBF是矩形,
∴CF=BD=10m,BF=CD=1.6m,
∵∠ACF=32.5°,
∴AF=CF tan32.5°=10×0.64≈6.4(m),
∴AB=AF+BF=6.4+1.6=8(m),
答:树AB的高度为8m;
“平面镜”方案:∵CD⊥BD,AB⊥BD,
∴∠CDE=∠ABE=90°,
∵∠CED=∠AEB,
∴△CDE∽△ABE,
∴,
∴,
∴AB=8,
答:树AB的高度为8m.
19.(8分)解:(1)样本容量为:14÷35%=40,
故A组人数为:40﹣10﹣14﹣4=12(人),
补全条形统计图如下:
(2)400180(人),
答:估计该校八年级参加测试的400名男生中成绩不低于10个的人数大约有180人;
(3)平均数表示抽取的40名学生的平均成绩;
众数表示抽取的40名学生中得分在某个分数的人数最多;
中位数表示取的40名学生中,将成绩从小到大排列后,位于中间位置的成绩(答案不唯一,任选其中一个说明即可).
20.(8分)解:(1)把点A(﹣3,0)坐标代入y=x+m得:0=﹣3+m,
解得m=3,
∴直线解析式为y=x+3,
把点B(n,4)坐标代入直线解析式得4=n+3,
解得n=1,
把点B(1,4)坐标代入反比例函数解析式得:4,
解得k=4,
∴反比例函数解析式为y,
(2)∵△AOC的面积小于△AOB的面积,
∴yC<yB,即yC<4,
∵点C在反比例函数图象上,且在第一象限,
∴4,
∴a>1.
21.(8分)(1)证明:连接OD,
在△OBD和△OBC中,
,
∴△OBD≌△OBC(SSS),
∴∠ODB=∠OCD=90°,
∴OD⊥AB,
∵OD是⊙O的半径,
∴AB是⊙O的切线;
(2)解:设⊙O的半径为R,
在Rt△OAD中,AD,AE=1,AO=AE+OE=1+R,OD=R,AD2+OD2=AO2,
∴()2+R2=(1+R)2,
解得R=1,
∴OD=1,
∴tan∠AOD,
∴∠AOD=60°,
∴∠COD=120°,
由(1)知△OBD≌△OBC,
∴∠BOD=∠BOC∠COD=60°,
∴的长.
22.(10分)解:(1)∵2x+y=80,
∴y=﹣2x+80,
∵S=xy,
∴S=x(﹣2x+80)=﹣2x2+80x;
(2)∵y≤42,
∴﹣2x+80≤42,
∴x≥19,
∴19≤x<40,
当S=750时,﹣2x2+80x=750,
x2﹣40x+375=0,
(x﹣25)(x﹣15)=0,
∴x=25,
∴当x=25m时,矩形实验田的面积S能达到750m2;
(3)∵S=﹣2x2+80x=﹣2(x2﹣40x)=﹣2(x2﹣40x+400﹣400)=﹣2(x﹣20)2+800,
∴当x=20m时,S有最大值800m2.
23.(11分)(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP1,
设EP=AP=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x,
∴EP=AP=x,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,即,
∴PH,
∵PG=AB=2,
∴GH=PG﹣PH.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HPPMy,
在Rt△PCH中,CHy,
∴BC=2CHy,
∴AD=BCy,
在Rt△APD中,APy,
∵BG∥AP,
∴△BMG∽△AMP,
∴,
∴BGy,
∴,
∴ABBG.
24.(12分)解:(1)∵二次函数y=﹣x2+bx+3与x轴交于A(﹣1,0),
∴0=﹣1﹣b+3,
解得:b=2;
(2)∵b=2,
∴二次函数表达式为:y=﹣x2+2x+3=﹣(x﹣1)2+4,
令y=0,解得x=﹣1或x=3,令x=0得y=3,
∴A(﹣1.0),B(3,0),C(0,3),
设M(m,﹣m2+2m+3),
作MH⊥x轴于点H,如图,
∵∠MAB=∠ACO,
∴tan∠MAB=tan∠ACO,即,
∴
解得m或m=﹣1(舍去),
∴﹣m2+2m+3=﹣()2+23,
∴M的坐标为(,);
(3)①∵将二次函数沿水平方向平移,
∴纵坐标不变为4,
∴图象L的解析式为y=﹣(x﹣n)2+4=﹣x2+2nx﹣n2+4,
∴N(0,﹣n2+4),
∴d=CN=|﹣n2+4﹣3|=|﹣n2+1|,
∴d;
②由①得d,画出大致图象如下,
∵d随着n增加而增加,
∴﹣1≤n≤0或n≥1,
△ABC中含(0,1),(0,2),(1,1)三个整点(不含边界),
当U内恰有2个整数点(0,1),(0,2)时,
当x=0时,yL>2,当x=1时,yL≤1,
∴,
∴n,n≥1或n≤1,
∴n<1,
∵﹣1≤n<0 或n≥1,
∴﹣1≤n≤1;
当U内恰有2个整数点(0,1),(1,1)时,
当x=0时,1<yL≤2,当x=1时,yL>1,
∴,
∴n或n,1n<1,
∴n,
∵﹣1≤n<0 或n≥1,
∴n;
当U内恰有2个整数点(0,2),(1,1)时,此种情况不存在,舍去.
综上所述,n的取值范围为﹣1≤n≤1或n.
(
1
/
30
)
一、选择题(共10题,每题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求)
1.在实际生产生活中,经常用正数、负数表示具有相反意义的量,如果把收入20元记作+20元,那么支出10元记作( )
A.+10元 B.﹣10元 C.+20元 D.﹣20元
2.如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
A. B. C. D.
3.计算2x 3x2的结果是( )
A.5x2 B.6x2 C.5x3 D.6x3
4.如图,一条公路的两侧铺设了AB,CD两条平行管道,并有纵向管道AC连通,若∠1=120°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
5.不等式x+1≥2的解集在数轴上表示正确的是( )
A. B.
C. D.
6.在下列事件中,必然事件是( )
A.掷一次骰子,向上一面的点数是3
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.任意画一个三角形,其内角和是180°
7.我国古代数学著作《九章算术》中记载了一个关于“方程”的问题:“今有牛五、羊二,直金十两,牛二、羊五,直金八两.问牛羊各直金几何?”译文:“今有牛5头,羊2头,共值金10两,牛2头,羊5头,共值金8两,问牛、羊每头各值金多少?”若设牛每头值金x两,羊每头值金y两,则可列方程组是( )
A. B.
C. D.
8.如图,AB是半圆O的直径,C为半圆O上一点,以点B为圆心,适当长为半径画弧,交BA于点M,交BC于点N,分别以点M,N为圆心,大于MN的长为半径画弧,两弧在∠ABC的内部相交于点D,画射线BD,连接AC.若∠CAB=50°,则∠CBD的度数是( )
A.30° B.25° C.20° D.15°
9.如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
10.已知抛物线y=ax2+bx+c(a,b,c为常数,a≠0)的顶点坐标为(﹣1,﹣2),与y轴的交点在x轴上方,下列结论正确的是( )
A.a<0 B.c<0 C.a﹣b+c=﹣2 D.b2﹣4ac=0
二、填空题(共5题,每题3分,共15分)
11.写出一个大于﹣1的数是 .
12.小亮了解了祖冲之、刘徽、赵爽、杨辉、秦九韶这5位著名数学家的生平简介,知晓他们取得的伟大成就对我国乃至世界数学发展起到的巨大推进作用,准备在数学课上随机选取其中一位的成就进行分享,选到数学家赵爽的概率是 .
13.铁的密度为7.9g/cm3,铁块的质量m(单位:g)与它的体积V(单位:cm3)之间的函数关系式为m=7.9V,当V=10cm3时,m= g.
14.计算的结果是 .
15.如图,由三个全等的三角形(△ABE,△BCF,△CAD)与中间的小等边三角形DEF拼成一个大等边三角形ABC.连接BD并延长交AC于点G.若AE=ED=2.则(1)∠FDB的度数是 ;(2)DG的长是 .
三、解答题(共9题,共75分、解答应写出文字说明、证明过程或演算步骤)
16.(6分)计算:(﹣1)×322﹣20240.
17.(6分)如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:BE=DF.
18.(6分)某数学兴趣小组在校园内开展综合与实践活动,记录如下:
活动项目 测量校园中树AB的高度
活动方案 “测角仪”方案 “平面镜”方案
方案示意图
实施过程 ①选取与树底B位于同一水平地面的D处; ②测量D,B两点间的距离; ③站在D处,用测角仪测量从眼睛C处看树顶A的仰角∠ACF; ④测量C到地面的高度CD. ①选取与树底B位于同一水平地面的E处; ②测量E,B两点间的距离; ③在E处水平放置一个平面镜,沿射线BE方向后退至D处,眼睛C刚好从镜中看到树顶A; ④测量E,D两点间的距离; ⑤测量C到地面的高度CD.
测量数据 ①DB=10m; ②∠ACF=32.5°; ③CD=1.6m. ①EB=10m; ②ED=2m; ③CD=1.6m.
备注 ①图上所有点均在同一平面内; ②AB,CD均与地面垂直; ③参考数据:tan32.5≈0.64. ①图上所有点均在同一平面内; ②AB,CD均与地面垂直; ③把平面镜看作一个点,并由物理学知识可得∠CED=∠AEB.
请你从以上两种方案中任选一种,计算树AB的高度.
19.(8分)某校为增强学生身体素质,以“阳光运动,健康成长”为主题开展体育训练,并对学生进行专项体能测试.以下是某次八年级男生引体向上测试成绩的抽样与数据分析过程.
【收集数据】随机抽取若干名男生的测试成绩.
【整理数据】将抽取的成绩进行整理,用x(引体向上个数)表示成绩,分成四组:
A组(0≤x<5),B组(5≤x<10),C组(10≤x<14),D组(x≥14).
【描述数据】根据抽取的男生成绩,绘制出如下不完整的统计图.
【分析数据】抽取的八年级男生测试成绩的平均数为8,中位数为8,众数为11.
根据以上信息,解答下列问题:
(1)求A组人数,并补全条形统计图;
(2)估计该校八年级参加测试的400名男生中成绩不低于10个的人数;
(3)从平均数、中位数和众数这三个统计量中任选一个,解释其在本题中的意义.
20.(8分)如图,一次函数y=x+m的图象与x轴交于点A(﹣3,0),与反比例函数y(k为常数,k≠0)的图象在第一象限的部分交于点B(n,4).
(1)求m,n,k的值;
(2)若C是反比例函数y的图象在第一象限部分上的点,且△AOC的面积小于△AOB的面积,直接写出点C的横坐标a的取值范围.
21.(8分)如图,在Rt△ABC中,∠ACB=90°,点E在AC上,以CE为直径的⊙O经过AB上的点D,与OB交于点F,且BD=BC.
(1)求证:AB是⊙O的切线;
(2)若AD,AE=1,求的长.
22.(10分)如图,某校劳动实践基地用总长为80m的栅栏,围成一块一边靠墙的矩形实验田,墙长为42m,栅栏在安装过程中不重叠、无损耗,设矩形实验田与墙垂直的一边长为x(单位:m),与墙平行的一边长为y(单位:m),面积为S(单位:m2).
(1)直接写出y与x,S与x之间的函数解析式(不要求写x的取值范围);
(2)矩形实验田的面积S能达到750m2吗?如果能,求x的值;如果不能,请说明理由;
(3)当x的值是多少时,矩形实验田的面积S最大?最大面积是多少?
23.(11分)在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
24.(12分)在平面直角坐标系中,抛物线y=﹣x2+bx+3与x轴交于点A(﹣1,0)和点B,与y轴交于点C.
(1)求b的值;
(2)如图,M是第一象限抛物线上的点,∠MAB=∠ACO,求点M的横坐标;
(3)将此抛物线沿水平方向平移,得到的新抛物线记为L,L与y轴交于点N,设L的顶点横坐标为n,NC的长为d.
①求d关于n的函数解析式;
②L与x轴围成的区域记为U,U与△ABC内部重合的区域(不含边界)记为W,当d随n的增大而增大,且W内恰好有两个横、纵坐标均为整数的点时,直接写出n的取值范围.
2024年湖北省中考数学试题参考答案
一、选择题(共10题,每题3分,共30分,在每题给出的四个选项中,只有一项符合题目要求)
1.B 2.A 3.D 4.B 5.A
6.D 7.A 8.C 9.B 10.C
二、填空题(共5题,每题3分,共15分)
11.0 12. 13.79 14.1 15.
三、解答题(共9题,共75分、解答应写出文字说明、证明过程或演算步骤)
16.(6分)解:原式=﹣3+3+4﹣1=3.
17.(6分)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
18.(6分)解:“测角仪”方案:过C作CF⊥AB于F,
∵CD⊥BD,AB⊥BD,
∴四边形CDBF是矩形,
∴CF=BD=10m,BF=CD=1.6m,
∵∠ACF=32.5°,
∴AF=CF tan32.5°=10×0.64≈6.4(m),
∴AB=AF+BF=6.4+1.6=8(m),
答:树AB的高度为8m;
“平面镜”方案:∵CD⊥BD,AB⊥BD,
∴∠CDE=∠ABE=90°,
∵∠CED=∠AEB,
∴△CDE∽△ABE,
∴,
∴,
∴AB=8,
答:树AB的高度为8m.
19.(8分)解:(1)样本容量为:14÷35%=40,
故A组人数为:40﹣10﹣14﹣4=12(人),
补全条形统计图如下:
(2)400180(人),
答:估计该校八年级参加测试的400名男生中成绩不低于10个的人数大约有180人;
(3)平均数表示抽取的40名学生的平均成绩;
众数表示抽取的40名学生中得分在某个分数的人数最多;
中位数表示取的40名学生中,将成绩从小到大排列后,位于中间位置的成绩(答案不唯一,任选其中一个说明即可).
20.(8分)解:(1)把点A(﹣3,0)坐标代入y=x+m得:0=﹣3+m,
解得m=3,
∴直线解析式为y=x+3,
把点B(n,4)坐标代入直线解析式得4=n+3,
解得n=1,
把点B(1,4)坐标代入反比例函数解析式得:4,
解得k=4,
∴反比例函数解析式为y,
(2)∵△AOC的面积小于△AOB的面积,
∴yC<yB,即yC<4,
∵点C在反比例函数图象上,且在第一象限,
∴4,
∴a>1.
21.(8分)(1)证明:连接OD,
在△OBD和△OBC中,
,
∴△OBD≌△OBC(SSS),
∴∠ODB=∠OCD=90°,
∴OD⊥AB,
∵OD是⊙O的半径,
∴AB是⊙O的切线;
(2)解:设⊙O的半径为R,
在Rt△OAD中,AD,AE=1,AO=AE+OE=1+R,OD=R,AD2+OD2=AO2,
∴()2+R2=(1+R)2,
解得R=1,
∴OD=1,
∴tan∠AOD,
∴∠AOD=60°,
∴∠COD=120°,
由(1)知△OBD≌△OBC,
∴∠BOD=∠BOC∠COD=60°,
∴的长.
22.(10分)解:(1)∵2x+y=80,
∴y=﹣2x+80,
∵S=xy,
∴S=x(﹣2x+80)=﹣2x2+80x;
(2)∵y≤42,
∴﹣2x+80≤42,
∴x≥19,
∴19≤x<40,
当S=750时,﹣2x2+80x=750,
x2﹣40x+375=0,
(x﹣25)(x﹣15)=0,
∴x=25,
∴当x=25m时,矩形实验田的面积S能达到750m2;
(3)∵S=﹣2x2+80x=﹣2(x2﹣40x)=﹣2(x2﹣40x+400﹣400)=﹣2(x﹣20)2+800,
∴当x=20m时,S有最大值800m2.
23.(11分)(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP1,
设EP=AP=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x,
∴EP=AP=x,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,即,
∴PH,
∵PG=AB=2,
∴GH=PG﹣PH.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HPPMy,
在Rt△PCH中,CHy,
∴BC=2CHy,
∴AD=BCy,
在Rt△APD中,APy,
∵BG∥AP,
∴△BMG∽△AMP,
∴,
∴BGy,
∴,
∴ABBG.
24.(12分)解:(1)∵二次函数y=﹣x2+bx+3与x轴交于A(﹣1,0),
∴0=﹣1﹣b+3,
解得:b=2;
(2)∵b=2,
∴二次函数表达式为:y=﹣x2+2x+3=﹣(x﹣1)2+4,
令y=0,解得x=﹣1或x=3,令x=0得y=3,
∴A(﹣1.0),B(3,0),C(0,3),
设M(m,﹣m2+2m+3),
作MH⊥x轴于点H,如图,
∵∠MAB=∠ACO,
∴tan∠MAB=tan∠ACO,即,
∴
解得m或m=﹣1(舍去),
∴﹣m2+2m+3=﹣()2+23,
∴M的坐标为(,);
(3)①∵将二次函数沿水平方向平移,
∴纵坐标不变为4,
∴图象L的解析式为y=﹣(x﹣n)2+4=﹣x2+2nx﹣n2+4,
∴N(0,﹣n2+4),
∴d=CN=|﹣n2+4﹣3|=|﹣n2+1|,
∴d;
②由①得d,画出大致图象如下,
∵d随着n增加而增加,
∴﹣1≤n≤0或n≥1,
△ABC中含(0,1),(0,2),(1,1)三个整点(不含边界),
当U内恰有2个整数点(0,1),(0,2)时,
当x=0时,yL>2,当x=1时,yL≤1,
∴,
∴n,n≥1或n≤1,
∴n<1,
∵﹣1≤n<0 或n≥1,
∴﹣1≤n≤1;
当U内恰有2个整数点(0,1),(1,1)时,
当x=0时,1<yL≤2,当x=1时,yL>1,
∴,
∴n或n,1n<1,
∴n,
∵﹣1≤n<0 或n≥1,
∴n;
当U内恰有2个整数点(0,2),(1,1)时,此种情况不存在,舍去.
综上所述,n的取值范围为﹣1≤n≤1或n.
(
1
/
30
)
同课章节目录
